25  Análisis espacial

25.1 General

25.1.1 Epidemiología espacial

Desde hace dos décadas se ha dedicado mucho interés a la modelación de datos espaciales. Estos análisis se han hecho en múltiples áreas del conocimiento, incluyendo a la geografía, geología, ciencias ambientales, economía, epidemiología, o medicina. En esta sección, explicaremos brevemente conceptos generales de análisis espacial aplicados a epidemiología.

Las técnicas de estadística clásica suponen estudiar variables aleatorias que se consideran independientes e idénticamente distribuidas (iid). Por ello, al momento de analizar fenómenos que varían en tiempo y espacio se requiere una modelación que considere la (auto)correlación espacial o temporal.

Cuando se tiene datos espaciales, intuitivamente se tiene la noción de que las observaciones cercanas están correlacionadas. Por ello, es necesario utilizar herramientas de análisis que consideren dicha estructura.

¿Por qué es especial lo espacial?

Primera Ley de Waldo Tobler

“Todo está relacionado con todo lo demás, pero las cosas más cercanas están más relacionadas que las distantes”. (Tobler, 1970)

Autocorrelación espacial

Es la correlación entre los valores de una sola variable estrictamente atribuible a sus posiciones de ubicación cercanas en una superficie bidimensional. Esto introduce una desviación del supuesto de iid.

Para medir la autocorrelación espacial existen test estadísticos, entre ellos:

• Test de Mantel

• Test de Moran

• Test C Geray

Para mayor detalle recomendamos la introducción del libro Geocomputation with R de Robin Lovelace, Jakub Nowosad, y Jannes Muenchow.

25.1.2 Terminología

Datos espaciales: Son todos los datos que presentan un sistema de referencia de coordenadas (SRC, CRS por sus siglas en inglés ).

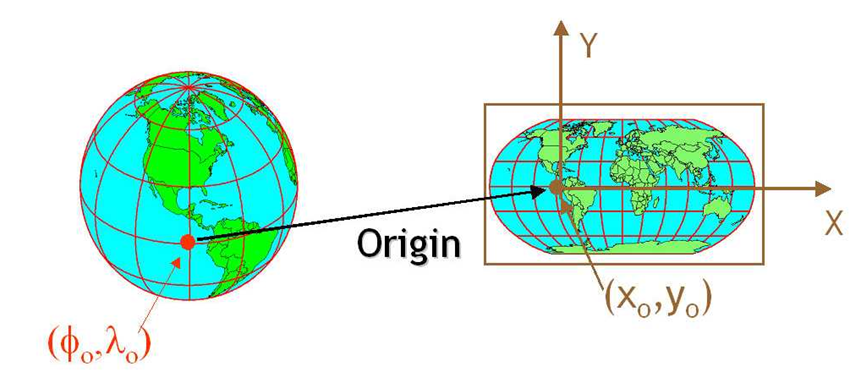
Sistemas de referencia de coordenadas: La Tierra tiene forma de un geoide y las proyecciones cartográficas intentan representar su superficie o una parte de ella en un plano (como el papel o la pantalla del computador).

Los SRC nos ayudan a establecer relaciones entre cualquier punto de la superficie terrestre y un plano de referencia, mediante proyecciones cartográficas. En general, los SRC se pueden dividir en:

• Geográficos

• Proyectados (también denominados Cartesianos o rectangulares)

Proyecciones geográficas: El uso de SRC geográficos es muy común; las proyecciones geográficas son las más empleadas. Están representadas por la latitud y longitud y tienen como unidad de medida a los grados sexagesimales. El sistema más popular se denomina WGS 84.

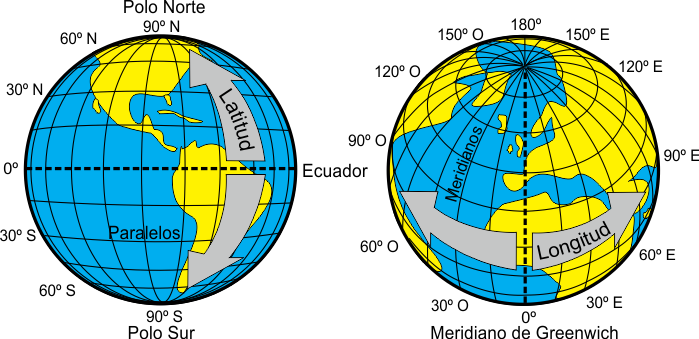
Proyecciones cartográficas: Entre todas las proyecciones que existen, ninguna es la mejor en un sentido absoluto, pues su utilidad depende de las necesidades específicas a la hora de usar el mapa.

La mayoría de las proyecciones que se emplean hoy en día en cartografía son proyecciones modificadas, híbridos entre varios tipos de proyecciones que minimizan las deformaciones y permiten alcanzar resultados predeterminados.

Según sus propiedades prevalecientes, las proyecciones se distinguen entre equidistantes, equivalentes y conformes, dependiendo de si mantienen la fidelidad representando distancias, áreas o ángulos respectivamente.

Según el tipo de superficie sobre el que se realiza la proyección, existen tres proyecciones básicas:

• Las proyecciones cilíndricas; son efectivas para representar las áreas entre los trópicos.

• La proyecciones cónicas; sirven para representar áreas en latitudes medias.

• Las proyecciones azimutales; sirven para representar zonas en altas latitudes.

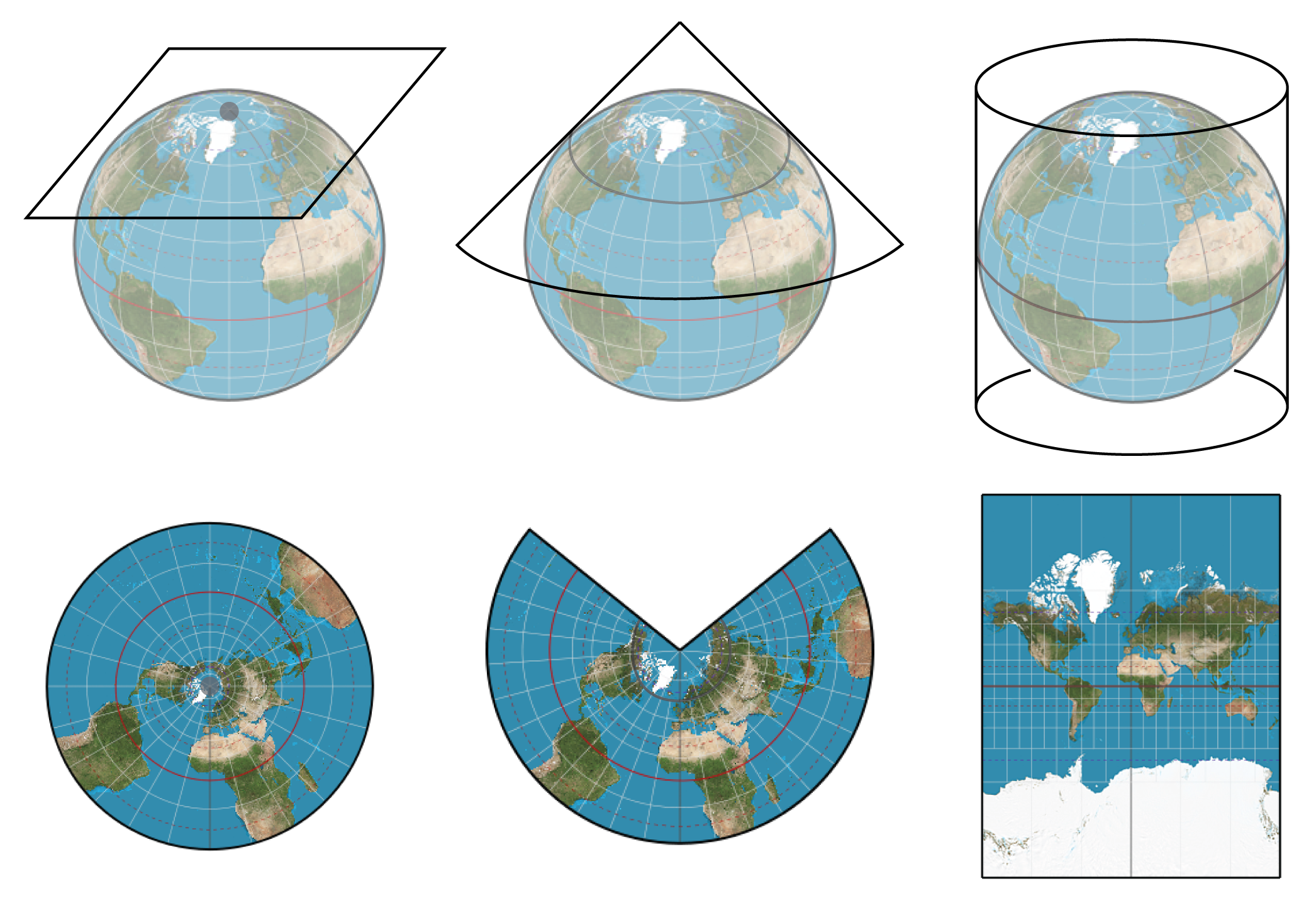
Universal Tranverse Mercator (UTM): Es la proyección cartográfica más empleada. Es una proyección cilíndrica conforme que gira el cilindro en 90 ° y divide el elipsoide de referencia en segmentos de 6 grados de ancho (60 segmentos para llegar a los 360°). UTM está diseñado para minimizar las distorsiones dentro de la misma área. Cerca del meridiano central, la distorsión es mínima y aumenta alejándose del meridiano. Es recomendable utilizar UTM sólo con mapas muy detallados.

Códigos EPSG: Todos los SRC llevan asociado un código que los identifica de forma única y a través del cual podemos conocer los parámetros asociados al mismo. Se le conoce como Spatial Reference System Identifier (SRID), y fue inicialmente impulsado por el European Petroleum Survey Group (EPSG).

Los códigos EPSG más conocidos son: - WGS84: 4326 - UTM zona 17N: 32617 - UTM zona 18N: 32618 - UTM zona 18S: 32718

25.2 Paquetes requeridos

Utilizaremos los siguientes paquetes (disponibles en CRAN o gitHub):

library(tidyverse)
library(sf)
library(mapview)
library(geodata)
library(ggspatial)
library(leaflet)
library(leaflet.extras2)
library(spdep)
library(sfdep)
library(spatstat)  
library(raster)
library(smacpod)
library(terra)
library(tidyterra)
library(stars)
library(gstat)
library(patchwork)
library(scanstatistics)
library(dbscan)

25.3 Manejo de datos vectoriales

La última estructura avanzada que exploraremos en este libro son las estructuras espaciales. R tiene un gran universo de paquetes para representación y análisis espacial. Actualmente existen dos formatos predominantes: sp y sf. Para los fines de este libro, utilizaremos sf, ya que tiene una integración natural con el ecosistema tidyverse.

El paquete sf hace referencia a simple feature ( Pebesma et al., 2016 ). Este formato codifica los datos espaciales en un formato que cumple con estándares formales (ISO 19125-1:2004). Esto enfatiza la geometría espacial de los objetos, de forma que los objetos están almacenados en bases de datos.

Existen múltiples variedades de representaciones gráficas con datos espaciales. En este libro, nos enfocaremos en la representación espacial de 1) patrones de puntos y 2) datos de polígonos ( e.j. por áreas administrativas ).

Utilizaremos la misma base que en la Capítulo 7 de Extensiones Gráficas de este libro. Esta base contiene datos ficticios usando como referencia los datos abiertos del Gobierno Peruano. Esta base contiene los registros de cada persona diagnosticada de COVID-19 por el Ministerio de Salud (MINSA) hasta el 24-MAY-2021.

Los datos de georefenciación (coordenadas) de los casos fueron simulados para los propósitos de este capítulo. Puede descargar directamente la base de datos del repositorio de Zenodo

covid <- read_csv("data/covid19-district.csv") 

FECHA_CORTE	UUID	DEPARTAMENTO	PROVINCIA	DISTRITO	METODODX	EDAD	SEXO	FECHA_RESULTADO	rango_edad	lon	lat
2021-05-22	d0d645886051560155bd16a8c34f4d9c	LIMA	LIMA	LIMA	PCR	66	MASCULINO	2020-04-02	60-79	-77.07894	-12.03991
2021-05-22	c646b803eba3e07df60d10b04fcd5f44	LIMA	LIMA	SAN JUAN DE LURIGANCHO	PR	22	MASCULINO	2020-09-01	20-39	-76.91957	-11.90625
2021-05-22	635b052d37b4a834d4260adb533a957b	LIMA	LIMA	COMAS	PCR	46	MASCULINO	2021-01-17	40-59	-77.03163	-11.91854
2021-05-22	ee2979a38d249069ed1d602e949d8be0	LIMA	LIMA	INDEPENDENCIA	PCR	32	MASCULINO	2020-05-17	20-39	-77.05800	-11.98330
2021-05-22	1c6754d9cbf8b6c9288c9519bf60d380	LIMA	LIMA	SAN JUAN DE MIRAFLORES	PR	58	MASCULINO	2020-07-31	40-59	-76.96537	-12.18076
2021-05-22	c82a40b40798b0b6ccb7f0e764d320c8	LIMA	LIMA	SAN JUAN DE MIRAFLORES	PR	56	MASCULINO	2020-05-11	40-59	-76.96170	-12.16064
2021-05-22	03fe28be18c2647a307f6126cb17d3ed	LIMA	LIMA	SAN BORJA	PCR	33	MASCULINO	2020-05-29	20-39	-77.00949	-12.10260
2021-05-22	9841e4e9a0ac00066ea5f5ca3ad0dae9	LIMA	LIMA	COMAS	PCR	31	MASCULINO	2021-01-08	20-39	-77.04477	-11.92656
2021-05-22	f10c27b98e7f4199412762e843ea8e7a	LIMA	LIMA	PUENTE PIEDRA	PCR	37	MASCULINO	2021-04-25	20-39	-77.09363	-11.93019
2021-05-22	2a29bbc2efa91c784ef2cb5ff9f6073e	LIMA	LIMA	INDEPENDENCIA	PCR	46	MASCULINO	2020-07-18	40-59	-77.03229	-11.99816
2021-05-22	a59fdda1c24907e99235fd6d97d0c211	LIMA	LIMA	LIMA	PCR	4	MASCULINO	2021-02-18	0-19	-77.04972	-12.04516
2021-05-22	b0dcca9d0865ab868c986a9dc68014dd	LIMA	LIMA	COMAS	PCR	59	MASCULINO	2020-11-10	40-59	-77.05364	-11.94359
2021-05-22	34f02c4013960608c0859af242d6d811	LIMA	LIMA	LA VICTORIA	PR	51	FEMENINO	2020-06-10	40-59	-77.02612	-12.06746
2021-05-22	ec774020dae03706ec9654158c060add	LIMA	LIMA	INDEPENDENCIA	PR	33	FEMENINO	2020-09-16	20-39	-77.03669	-11.97019
2021-05-22	b65b2747e0a8b33c73243df94baeb61c	LIMA	LIMA	SAN JUAN DE MIRAFLORES	PR	29	FEMENINO	2021-02-15	20-39	-76.95665	-12.18571
2021-05-22	c8be830e10f60ff524e0e0b0e28c07da	LIMA	LIMA	SANTA ANITA	PCR	38	FEMENINO	2021-03-30	20-39	-76.98286	-12.05073
2021-05-22	a386b33233bdf433edc3ec8cfce726c9	LIMA	LIMA	LOS OLIVOS	AG	65	FEMENINO	2021-01-15	60-79	-77.07344	-11.96249
2021-05-22	0630269134a37a4989fa973c9644bf6f	LIMA	LIMA	ATE	PR	51	MASCULINO	2020-05-09	40-59	-76.93608	-12.05348
2021-05-22	9dbf32b3cd42f37602bd23d296d326e3	LIMA	LIMA	SAN MIGUEL	AG	15	FEMENINO	2021-04-05	0-19	-77.09004	-12.07787
2021-05-22	d554666df8ae12cfa88b6423e7c9131f	LIMA	LIMA	BREÑA	PCR	59	FEMENINO	2021-02-21	40-59	-77.05752	-12.06692

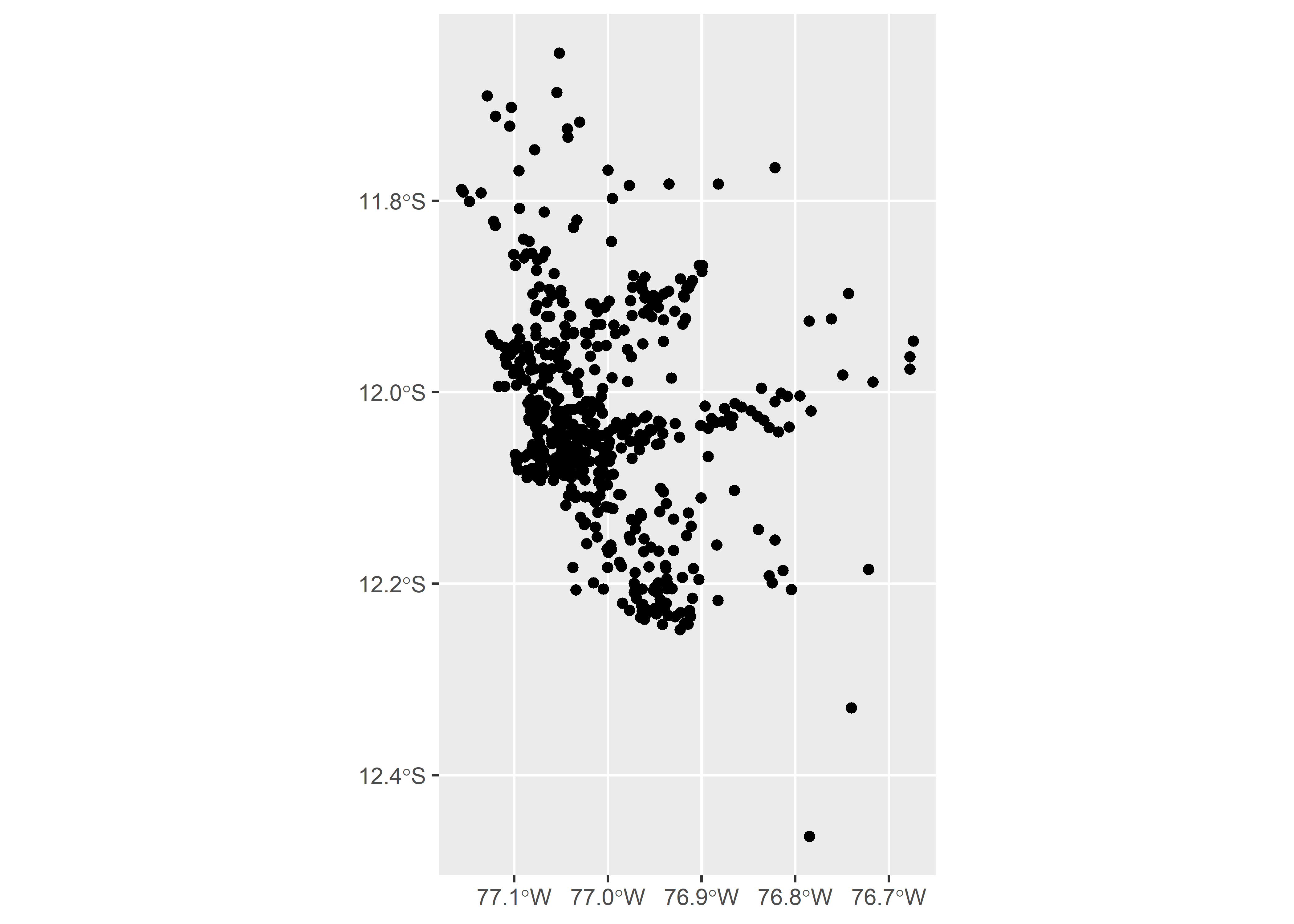
25.3.1 Patrones de puntos

Si tenemos una base de datos georeferenciada (con coordenadas geográficas para cada observación), podemos utilizar estos valores ( coordenadas ) para transformar nuestra base de datos tabular en una base de datos espacial.

Usaremos la función st_as_sf() para especificar los valores de latitud y longitud. Adicionalmente, tenemos que especificar el sistema de referencia de coordenadas (CRS en ingles) con que fueron georeferenciados nuestros datos en el área de estudio ( ej. crs = 4326 ).

covid_p <- covid %>%
  st_as_sf(coords = c("lon", "lat"), crs = 4326)

Haremos un gráfico simple usando ggplot2 y la geometría geom_sf().

covid_p %>%
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  ggplot() +
  geom_sf() 

Para visualizar nuestro mapa de una forma dinámica podemos usar el paquete mapview().

m_p <- covid_p %>% 
  filter(FECHA_RESULTADO == "2020-12-10") %>%
  mapview(layer.name = "puntos")

m_p

25.3.2 Datos en polígonos

Para realizar las representaciones de las áreas necesitamos un archivo que contiene la geometría espacial (los bordes). Hay varios formatos, pero el más conocido es el shapefile (.shp).

Uno puede cargar los datos del archivo .shp usando la función st_read(). Para este taller, utilizaremos el paquete geodata que contiene los datos espaciales de las divisiones políticas de todos los países. geodata descarga datos en formato SpatVector el cual transformaremos a un objeto sf con la función st_as_sf().

peru <- gadm(country = "PER", level = 3, path= ".", resolution = 2)
  
lima_sf <- peru %>%
  st_as_sf() %>%
  # Filtramos los datos espaciales solo de Lima metropolitana
  filter(NAME_2 == "Lima") %>%
  # Editamos algunos errores en nuestros datos espaciales
  mutate(NAME_3 = ifelse(NAME_3 == "Magdalena Vieja",
                         "Pueblo Libre", NAME_3))

Ahora, procesaremos los datos de la base covid_count (base de datos tipo panel para cada fecha/distrito que construimos en la sección anterior) y los datos espaciales lim_sf para poder hacer la unión.

covid_count <- covid %>%
  group_by(DISTRITO, FECHA_RESULTADO) %>%
  summarise(casos = n()) %>%
  ungroup() %>%
  complete(FECHA_RESULTADO = seq.Date(
    min(FECHA_RESULTADO, na.rm = T),
    max(FECHA_RESULTADO, na.rm = T), 
    by = "day"),
    nesting(DISTRITO), 
    fill = list(casos = 0)
  )

`summarise()` has grouped output by 'DISTRITO'. You can override using the
`.groups` argument.

covid_sf <- lima_sf %>%
  mutate(DISTRITO = toupper(NAME_3)) %>%
  full_join(covid_count, by = "DISTRITO", "FECHA_RESULTADO")

class(covid_sf)

[1] "sf"         "data.frame"

Haremos un gráfico simple para verificar que nuestros datos estén ubicados en el lugar correcto.

covid_sf %>%
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  ggplot() +
  geom_sf()

m_sf <- covid_sf %>% 
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  mapview(layer.name = "distritos")

m_sf

25.3.3 Múltiples capas

Los contenidos en los mapas suelen representarse como capas que se pueden combinar y sobreponer para entender el evento de interés.

Cada capa es agregada como una geometría diferente con geom_sf(). En mapview, podemos usar el símbolo + para graficar ambas capas.

ggplot() +
  geom_sf(data = covid_sf %>% 
            filter(FECHA_RESULTADO == "2020-12-11")) + 
  geom_sf(data = covid_p %>% 
            filter(FECHA_RESULTADO == "2020-12-11"))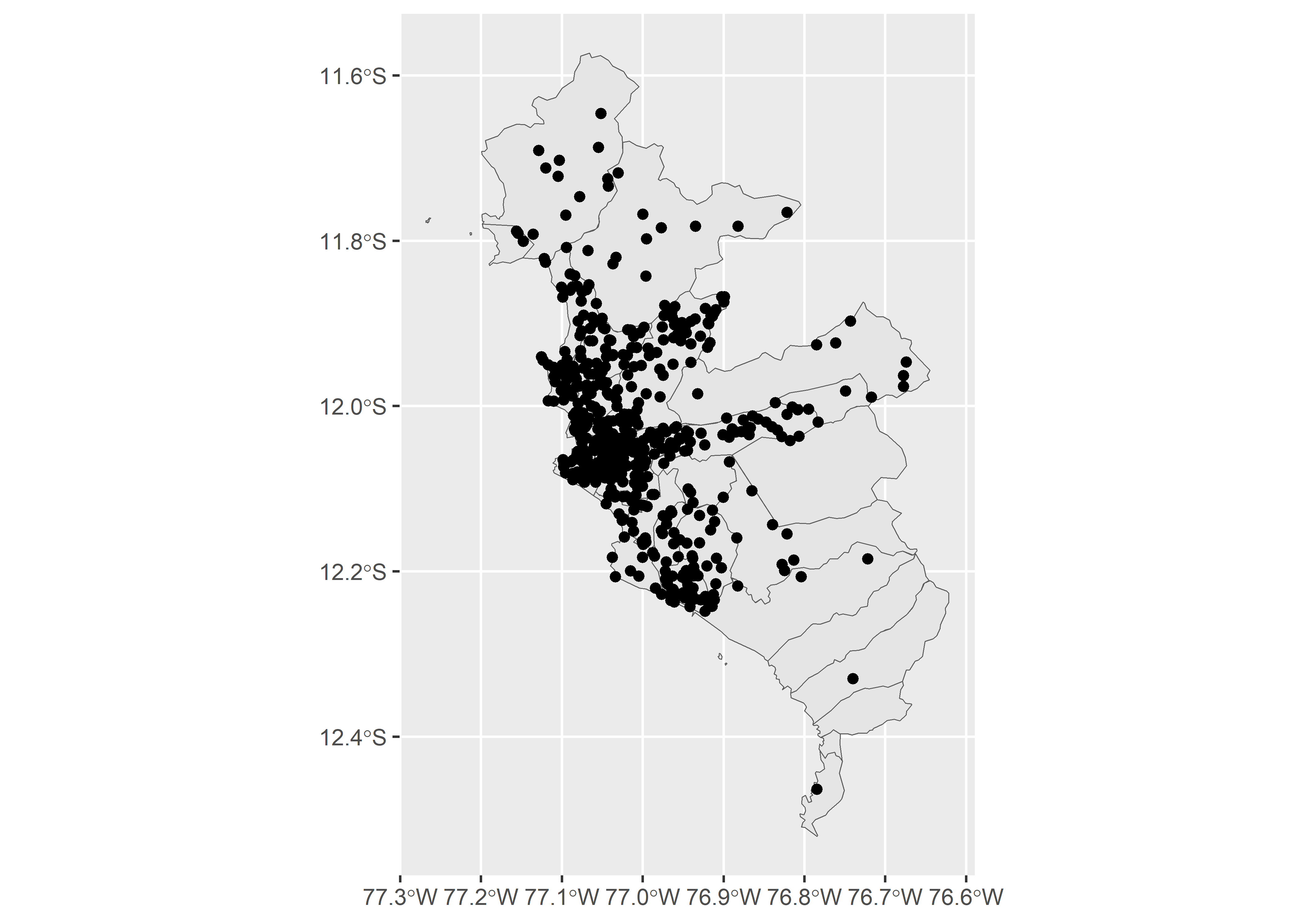

m_p + m_sf

25.4 Manejo de datos grillados (raster)

25.4.1 Introducción a los Datos Grillados (Rasters)

25.4.1.1 Definición y Conceptos Básicos

25.4.1.1.1 ¿Qué es un raster?

El modelo de datos espaciales ráster representa el mundo con la cuadrícula continua de celdas (a menudo también llamadas píxeles).

25.4.1.1.2 Celdas/píxeles que componen los rasters

Este modelo de datos se refiere a menudo a las llamadas cuadrículas regulares, en las que cada celda tiene el mismo tamaño constante, en este libro se analizarán las cuadrículas regulares. Sin embargo, existen otros tipos de cuadrículas, como las cuadrículas rotadas, cizalladas, rectilíneas y curvilíneas.

El modelo de datos ráster suele constar de una cabecera ráster y una matriz (con filas y columnas) que representa celdas espaciadas por igual.

25.4.1.1.3 Parámetros generales de los rasters

El header del raster define el sistema de referencia de coordenadas, la extensión y el origen. El origen (o punto de partida) suele ser la coordenada de la esquina inferior izquierda de la matriz.

El header define la extensión mediante el número de columnas, el número de filas y la resolución del tamaño de las celdas.

La resolución puede ser calculada de la siguiente manera:

\[ \text{resolution} = \left( \frac{\text{xmax} - \text{xmin}}{\text{ncol}}, \frac{\text{ymax} - \text{ymin}}{\text{nrow}} \right) \] Partiendo del origen, podemos acceder fácilmente a cada celda y modificarla utilizando el ID de una celda.

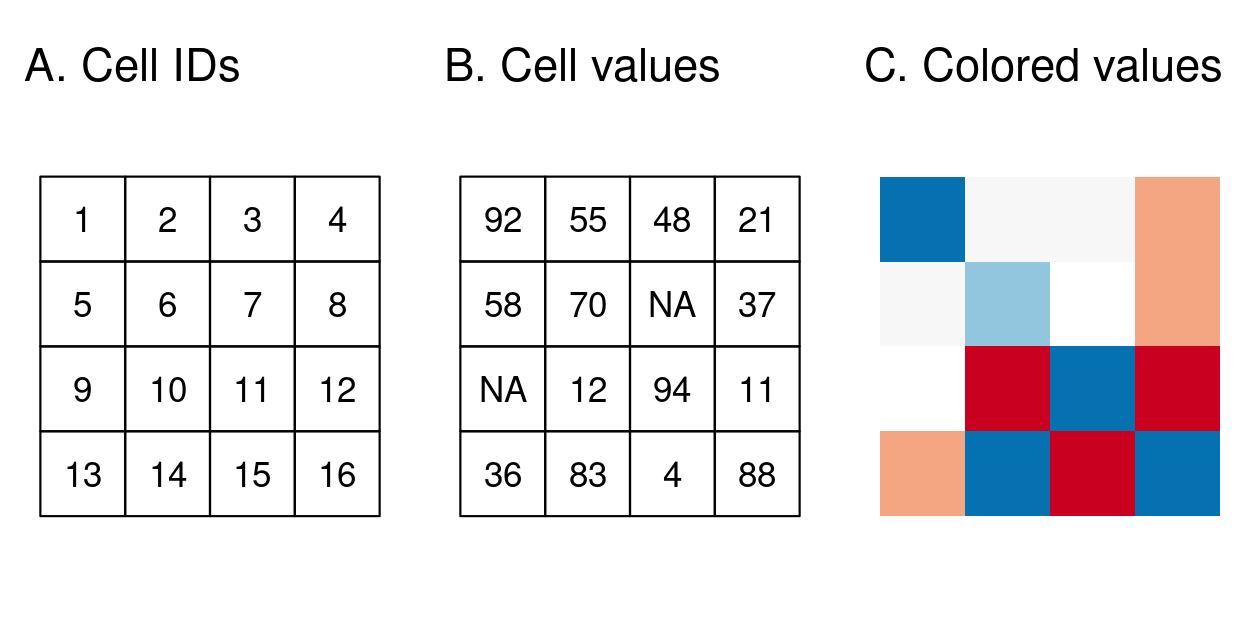
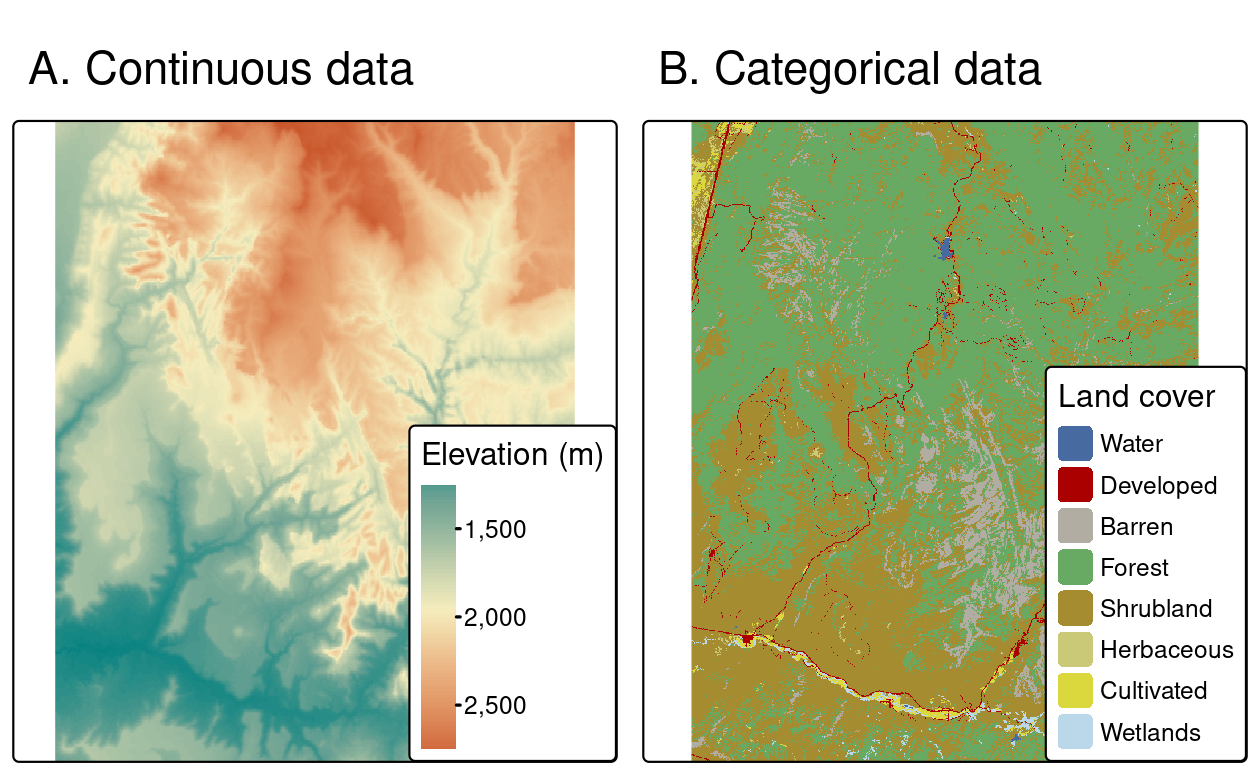
Los mapas raster suelen representar fenómenos continuos como la elevación, la temperatura, la densidad de población o datos espectrales. En el modelo de datos raster también pueden representarse características discretas, como clases de suelo o de cubierta terrestre.

Dependiendo de la naturaleza de la aplicación, las representaciones vectoriales de características discretas pueden ser más adecuadas.

25.4.2 Paquetes de R para trabajar con Datos Raster

Durante las dos últimas décadas, se han desarrollado varios paquetes para leer y procesar conjuntos de datos raster. El principal de ellos fue raster, que supuso un cambio radical en las capacidades raster de R cuando se lanzó en 2010 y se convirtió en el principal paquete en este ámbito hasta el desarrollo de terra y stars. Ambos paquetes, desarrollados más recientemente, ofrecen funciones potentes y eficaces para trabajar con conjuntos de datos ráster, y existe un solapamiento sustancial entre sus posibles casos de uso.

En este libro nos centraremos en terra, que sustituye al antiguo y (en la mayoría de los casos) más lento raster. Antes de aprender cómo funciona el sistema de clases de terra, esta sección describe las similitudes y diferencias entre terra y stars; este conocimiento ayudará a decidir cuál es el más apropiado en diferentes situaciones.

25.4.2.1 Entendiendo el paquete Terra

En primer lugar, terra se centra en el modelo de datos ráster más común (cuadrículas regulares) y maneja rásters de una o varias capas. Es importante destacar que todas las capas o elementos de un cubo de datos deben tener las mismas dimensiones espaciales y extensión.

En segundo lugar, Terra permite leer todos los datos ráster en memoria o sólo leer sus metadatos, lo que suele hacerse automáticamente en función del tamaño del archivo de entrada. El almacenamiento de los valores en ráster está basado en código C++ y utiliza principalmente punteros C++.

En tercer lugar, las funciones que terra utiliza su propia clase de objetos para datos vectoriales SpatVector, pero también acepta los de sf.

En cuarto lugar, Terra se basa principalmente en un gran número de funciones incorporadas, donde cada función tiene un propósito específico (por ejemplo, remuestreo o recorte).

25.4.3 Carga y Exploración de Datos Raster en R

25.4.3.1 Introducción a terra

El paquete terra soporta objetos raster en R. Proporciona un amplio conjunto de funciones para crear, leer, exportar, manipular y procesar conjuntos de datos raster. La funcionalidad de terra es en gran medida la misma que la del paquete raster, más maduro, pero hay algunas diferencias: las funciones de terra suelen ser más eficientes computacionalmente que las equivalentes de raster. Por otra parte, el sistema de clases raster es popular y utilizado por muchos otros paquetes.

Por ejemplo, srtm.tif es un modelo digital de elevación de la zona del Parque Nacional de Zion (Utah, EE.UU.)

my_rast = terra::rast("figures/spat/srtm.tif")
class(my_rast)

[1] "SpatRaster"
attr(,"package")
[1] "terra"

Al escribir el nombre del raster en la consola, se imprimirá la cabecera del raster (dimensiones, resolución, extensión, CRS) y alguna información adicional (clase, fuente de datos, resumen de los valores del raster):

my_rast

class       : SpatRaster 
dimensions  : 457, 465, 1  (nrow, ncol, nlyr)
resolution  : 0.0008333333, 0.0008333333  (x, y)
extent      : -113.2396, -112.8521, 37.13208, 37.51292  (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat WGS 84 (EPSG:4326) 
source      : srtm.tif 
name        : srtm 
min value   : 1024 
max value   : 2892 

Funciones específicas de cada componente: dim() devuelve el número de filas, columnas y capas; ncell() el número de celdas (píxeles); res() la resolución espacial; ext() su extensión espacial; y crs() su sistema de referencia de coordenadas.

25.4.3.2 Preparación básica de mapas

De forma similar al paquete sf, terra también proporciona métodos plot() para sus propias clases.

ggplot() + geom_spatraster(data = my_rast) +
  scale_fill_viridis_c(option = "plasma") +
  theme_minimal()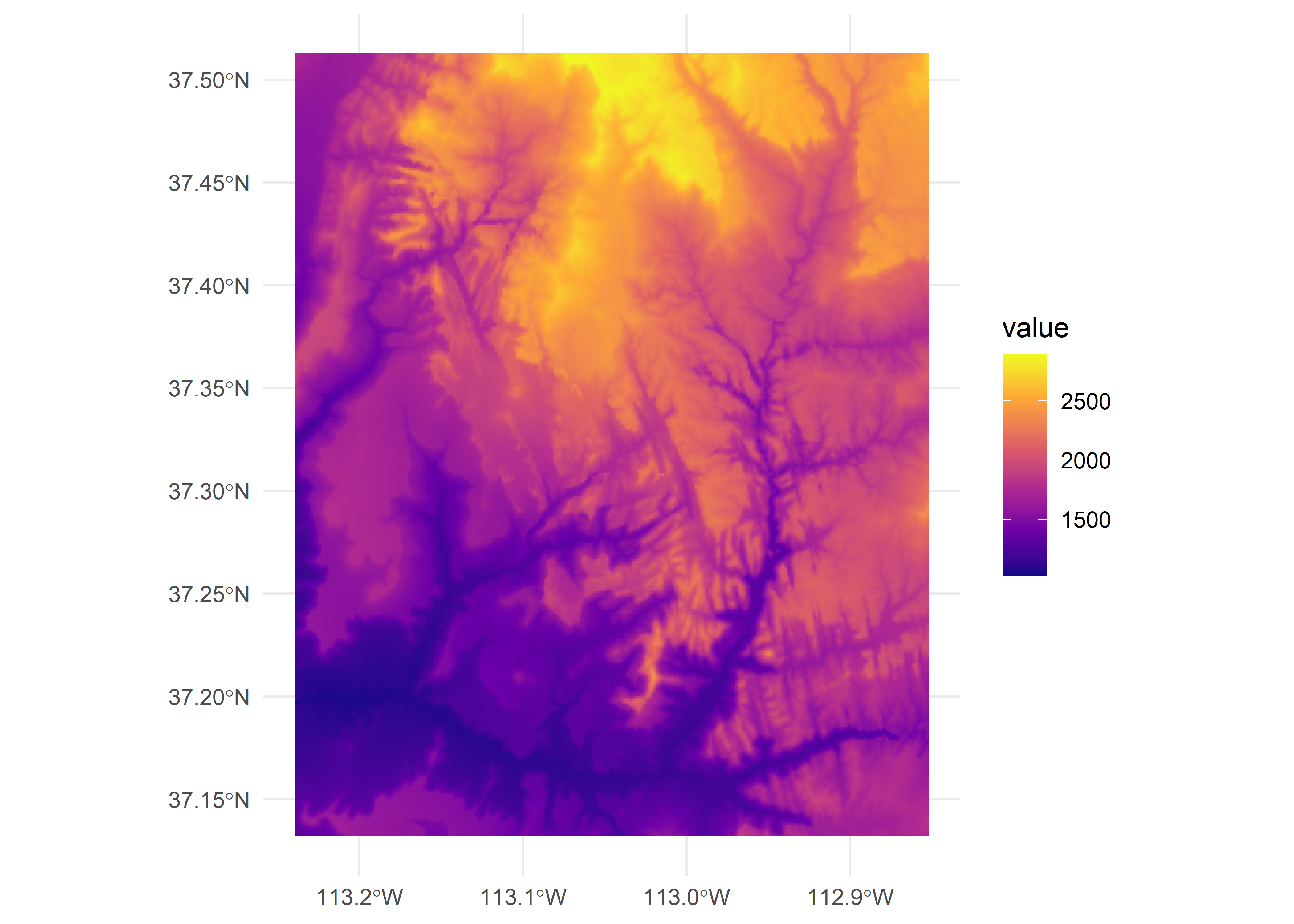

Existen otros enfoques para trazar datos raster en R que están fuera del alcance de esta sección, incluyendo:

La función plotRGB() del paquete terra para crear un gráfico basado en tres capas de un objeto SpatRaster Paquetes como tmap para crear mapas estáticos e interactivos de objetos ráster y vectoriales. Funciones, por ejemplo levelplot() del paquete rasterVis, para crear facetas, una técnica habitual para visualizar cambios a lo largo del tiempo.

25.4.3.3 Clases en Raster

La clase SpatRaster representa objetos raster de terra. La forma más fácil de crear un objeto raster en R es leer un archivo raster desde el disco o desde un servidor

single_rast = rast("figures/spat/srtm.tif")

single_rast

class       : SpatRaster 
dimensions  : 457, 465, 1  (nrow, ncol, nlyr)
resolution  : 0.0008333333, 0.0008333333  (x, y)
extent      : -113.2396, -112.8521, 37.13208, 37.51292  (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat WGS 84 (EPSG:4326) 
source      : srtm.tif 
name        : srtm 
min value   : 1024 
max value   : 2892 

Los raster también pueden crearse desde cero utilizando la misma función rast(). Esto se ilustra en el siguiente fragmento de código, que da como resultado un nuevo objeto SpatRaster. El raster resultante consiste en 36 celdas (6 columnas y 6 filas especificadas por nrows y ncols) centradas alrededor del Primer Meridiano y el Ecuador (ver parámetros xmin, xmax, ymin y ymax). Se asignan valores (vals) a cada celda: 1 a la celda 1, 2 a la celda 2, etc.

Recuerde: rast() rellena las celdas por filas (a diferencia de matrix()) empezando por la esquina superior izquierda, lo que significa que la fila superior contiene los valores del 1 al 6, la segunda del 7 al 12, etc. Para otras formas de crear objetos raster, véase ?rast.

new_raster = rast(nrows = 6, ncols = 6, 
                  xmin = -1.5, xmax = 1.5, ymin = -1.5, ymax = 1.5,
                  vals = 1:36)

ggplot() + geom_spatraster(data = new_raster) +
  scale_fill_viridis_c(option = "cividis") +
  theme_minimal()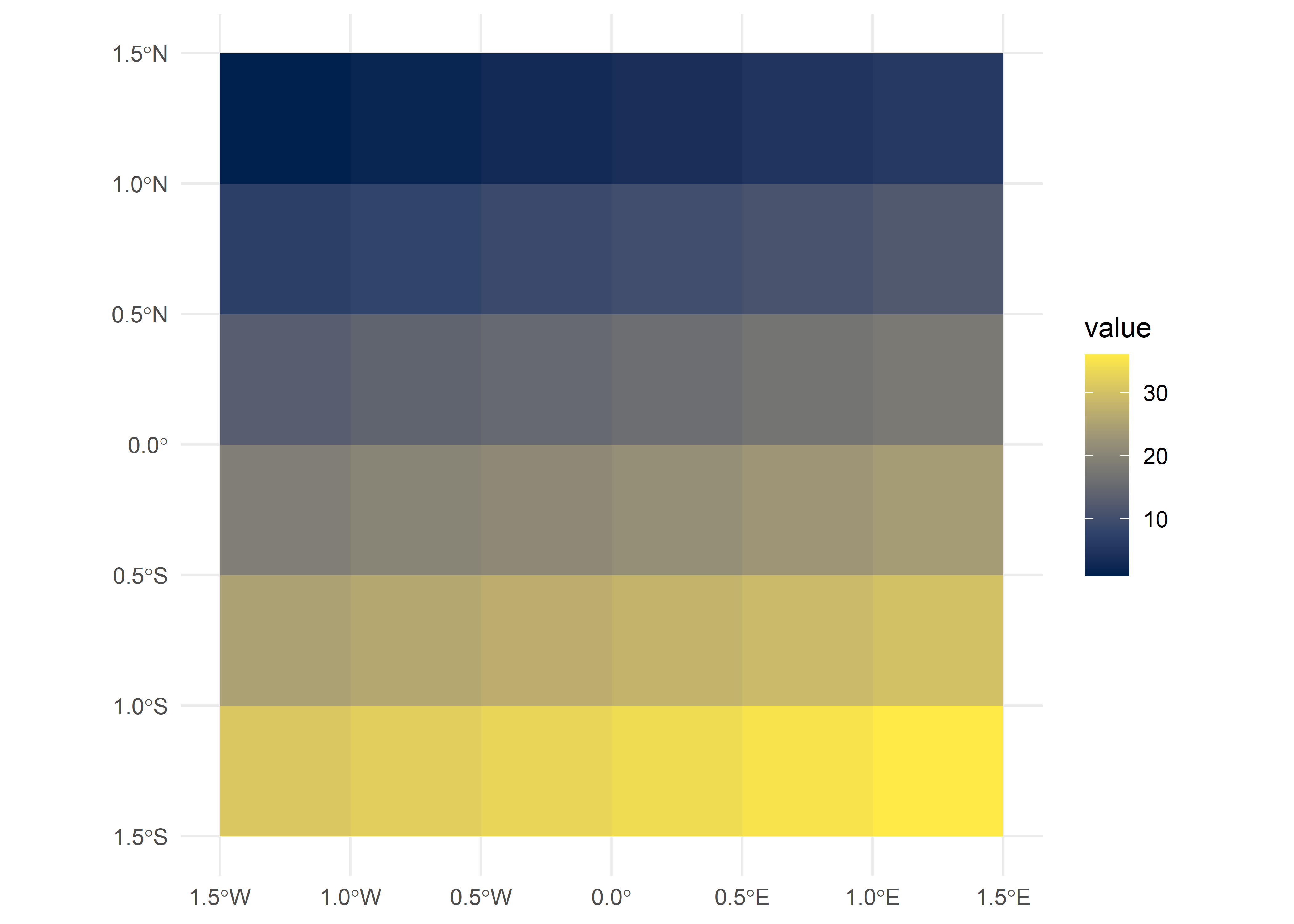

La clase SpatRaster también maneja múltiples capas, que suelen corresponder a un único archivo de satélite multiespectral o a una serie temporal de rásters.

multi_rast = rast("figures/spat/landsat.tif")

multi_rast

class       : SpatRaster 
dimensions  : 1428, 1128, 4  (nrow, ncol, nlyr)
resolution  : 30, 30  (x, y)
extent      : 301905, 335745, 4111245, 4154085  (xmin, xmax, ymin, ymax)
coord. ref. : WGS 84 / UTM zone 12N (EPSG:32612) 
source      : landsat.tif 
names       : landsat_1, landsat_2, landsat_3, landsat_4 
min values  :      7550,      6404,      5678,      5252 
max values  :     19071,     22051,     25780,     31961 

Verificamos las 4 capas y las visualizamos

ggplot() + geom_spatraster(data = multi_rast) +
  facet_wrap(~lyr, ncol = 2) +
  scale_fill_viridis_c(option = "viridis") +
  theme_minimal()

<SpatRaster> resampled to 500684 cells.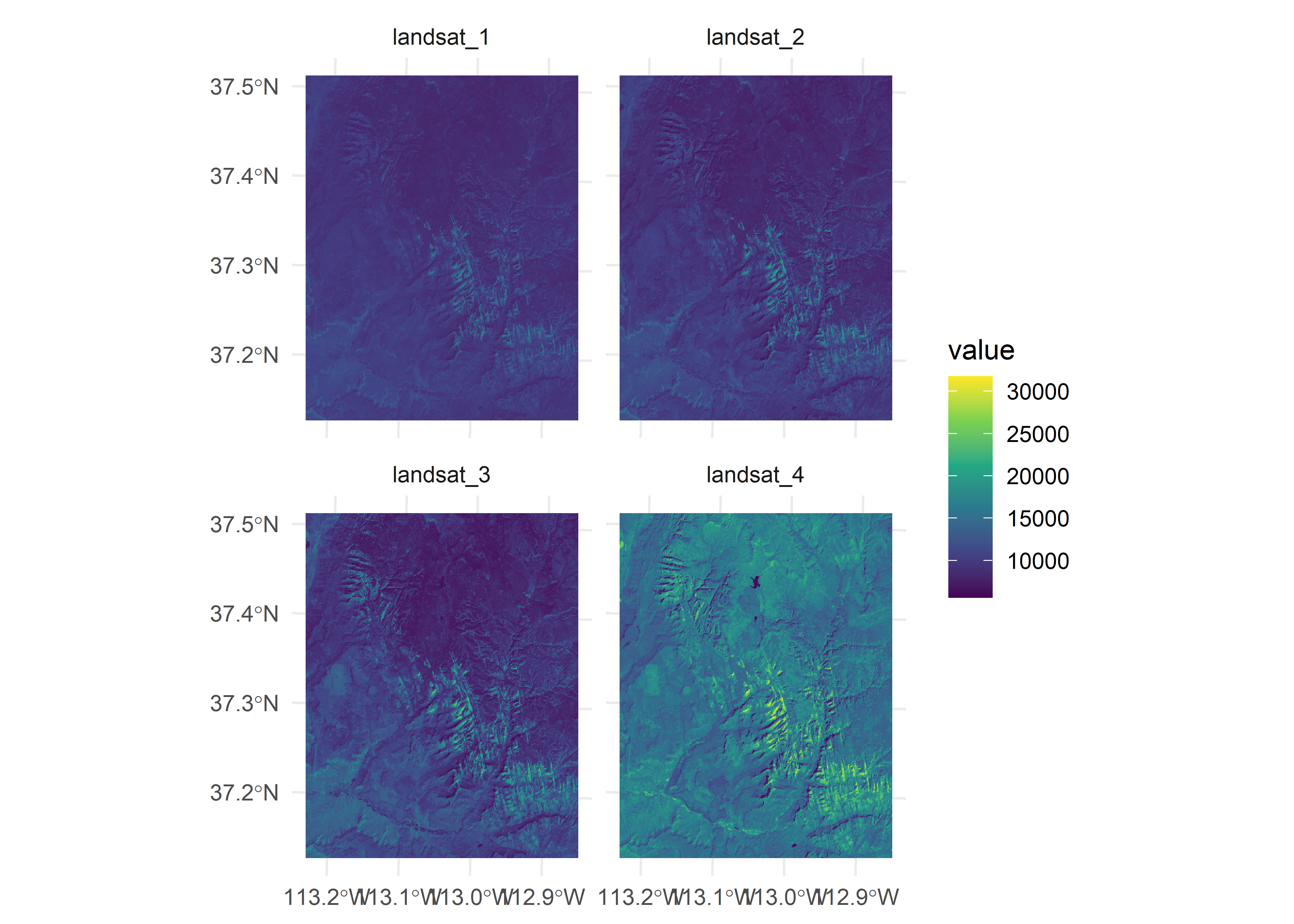

Probando el plotRGB(). Primero tenemos que normalizar los datos para que estén de 0 a 1 según los requisitos de la función.

nlyr() recupera el número de capas almacenadas en un objeto SpatRaster:

nlyr(multi_rast)

[1] 4

También podemos convertir otro formato de imagen a TIFF solo con la función rast()

multi_rast2 = rast("figures/spat/SK5639.jpg")

Warning: [rast] unknown extent

ggplot() + geom_spatraster(data = multi_rast2$SK5639_1) +
  facet_wrap(~lyr, ncol = 2) +
  scale_fill_viridis_c(option = "viridis") +
  theme_minimal()

25.4.3.3.1 Seleccionar capas de interés

Para objetos ráster multicapa, las capas pueden seleccionarse con los operadores [[ y $, por ejemplo con los comandos multi_rast[[“landsat_1”]] y multi_rast $landsat_1. También se puede utilizar terra::subset() para seleccionar capas. Acepta un número de capa o su nombre como segundo argumento:

multi_rast3 = subset(multi_rast, 3)
multi_rast4 = subset(multi_rast, "landsat_4")

25.4.3.3.2 Combinar capas de interés

La operación contraria, combinar varios objetos SpatRaster en uno solo, puede realizarse mediante la función:

multi_rast34 = c(multi_rast3, multi_rast4)

25.4.4 Manipulación y Procesamiento de Datos Raster

25.4.4.1 Cropping, enmascaramiento y agregación con Datos Raster

El paquete terra proporciona varias funciones para trabajar con datos raster. Aquí mostramos ejemplos de cómo recortar, enmascarar y agregar datos ráster utilizando un archivo ráster que representa datos de temperatura. En primer lugar, utilizamos la función worldclim_country() del paquete geodata para descargar datos globales de temperatura de la base de datos WorldClim. En concreto, descargamos la temperatura media mensual en grados centígrados especificando el país (country = “Peru”), la variable temperatura media (var = “tavg”), la resolución (res = 10) y la ruta donde descargar los datos como archivo temporal (path = tempdir()). Visualizamos el mapa con mapview()para navegar a través del mismo:

r <- geodata::worldclim_country(country = "Peru", var = "tavg",
                                res = 10, path = tempdir())
mapview(r, maxpixels = 41558400)

Podemos promediar los datos ráster de temperatura a lo largo de los meses con la función mean().

r <- mean(r)

ggplot() +
  geom_spatraster(data = r) +
  scale_fill_viridis_c(option = "magma") +
  theme_minimal()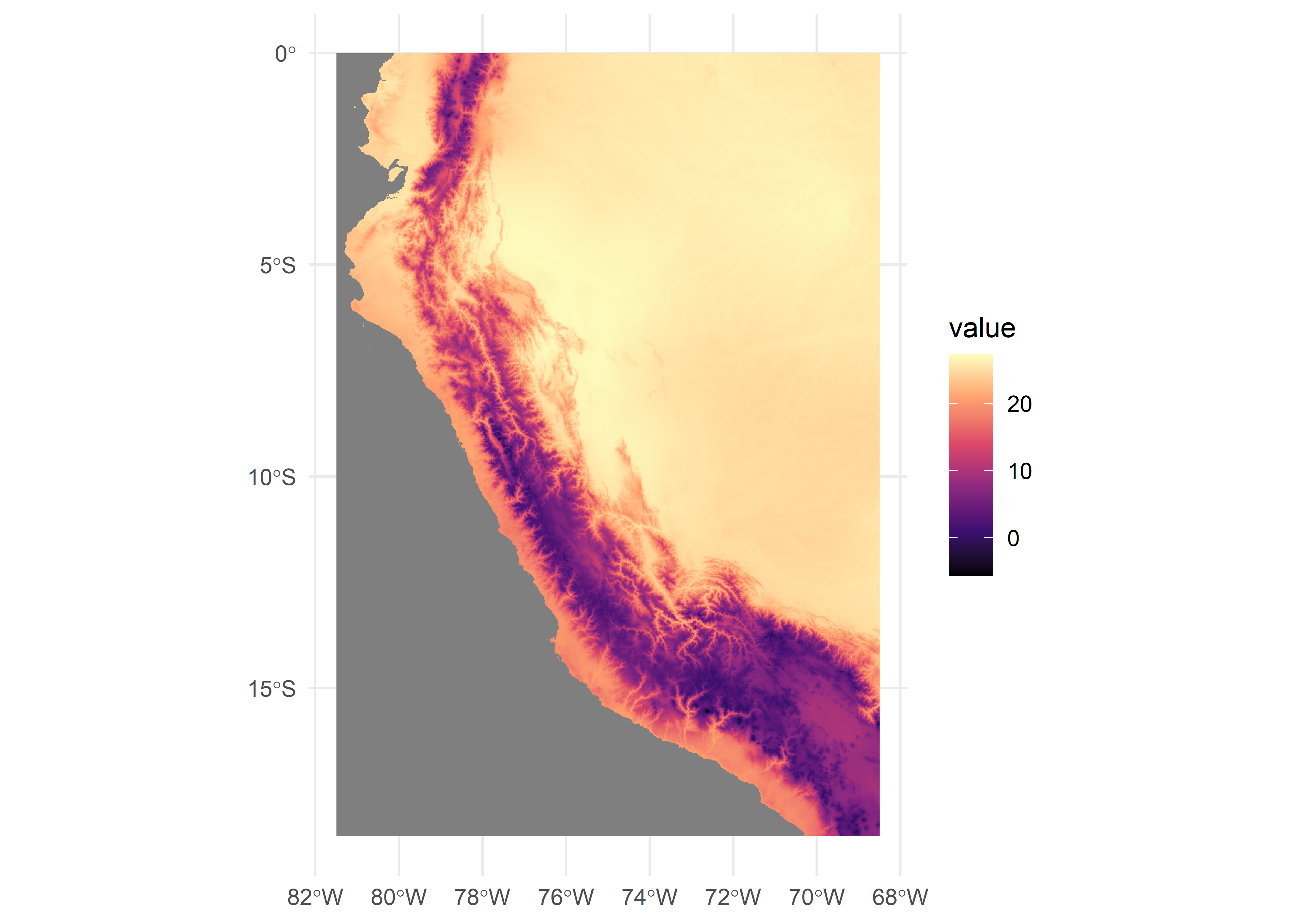

También podemos descargar el mapa de Perú con el paquete rnaturalearth.

# Mapa

# map_1 <- rnaturalearth::ne_states("Peru", returnclass = "sf")

map_1 <- st_read("files/shapefiles/mapa_peru.shp")

Reading layer `mapa_peru' from data source 
  `D:\Github\r4pubh\files\shapefiles\mapa_peru.shp' using driver `ESRI Shapefile'
Simple feature collection with 26 features and 121 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: -81.33756 ymin: -18.33775 xmax: -68.68425 ymax: -0.02909271
Geodetic CRS:  WGS 84

map_2 <- map_1 %>%
  filter(name == "Loreto") # Se pueden borrar regiones que no sean de interés

ggplot(map_2) + geom_sf()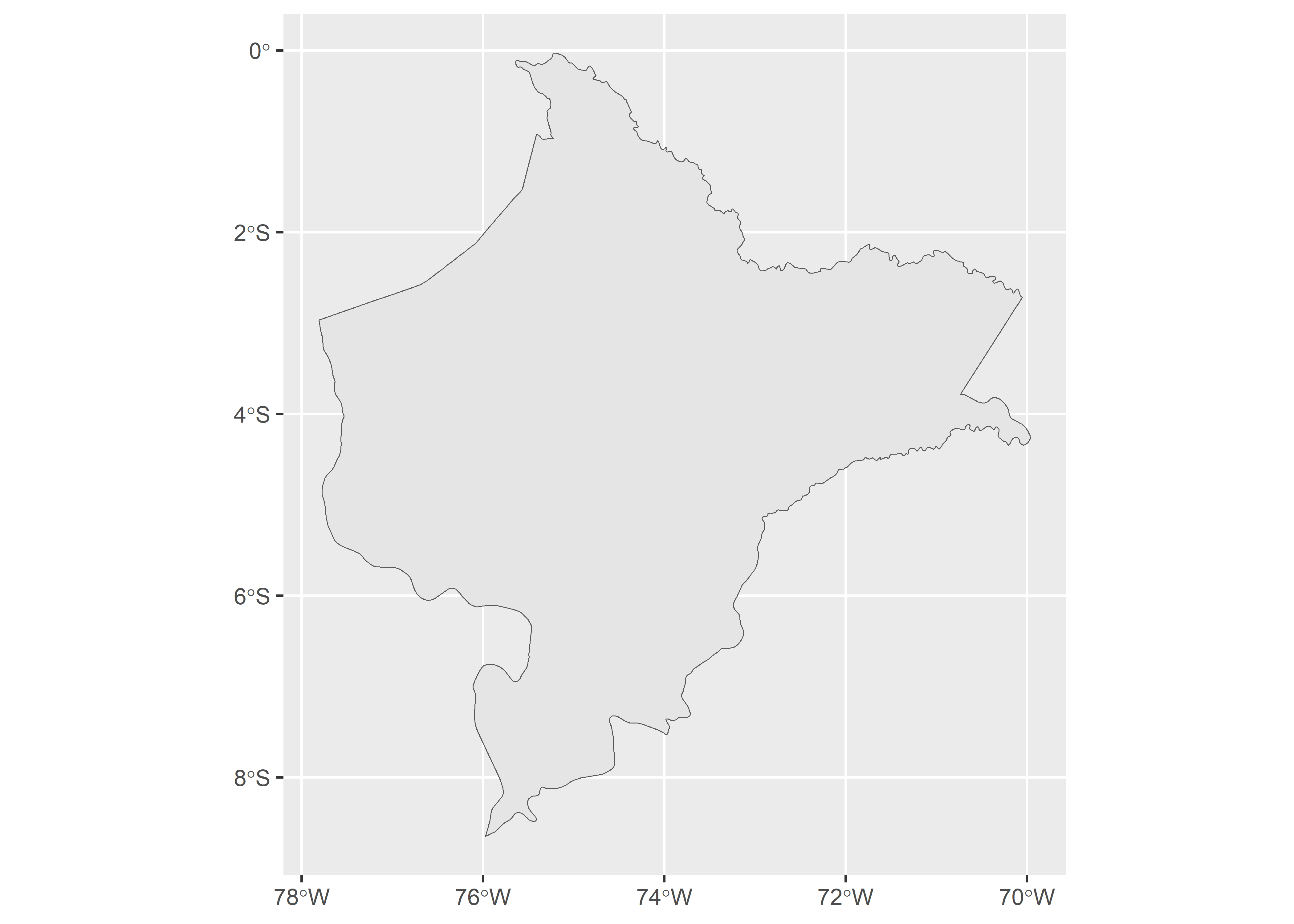

25.4.4.1.1 Cropping

Obtenemos la extensión espacial del mapa con terra:ext(). A continuación, podemos utilizar crop() para eliminar la parte del raster que queda fuera de la extensión espacial.

r <- mean(r)

sextent <- terra::ext(map_2)
r <- terra::crop(r, sextent)

ggplot() +
  geom_spatraster(data = r) +
  scale_fill_viridis_c(option = "magma") +
  theme_minimal()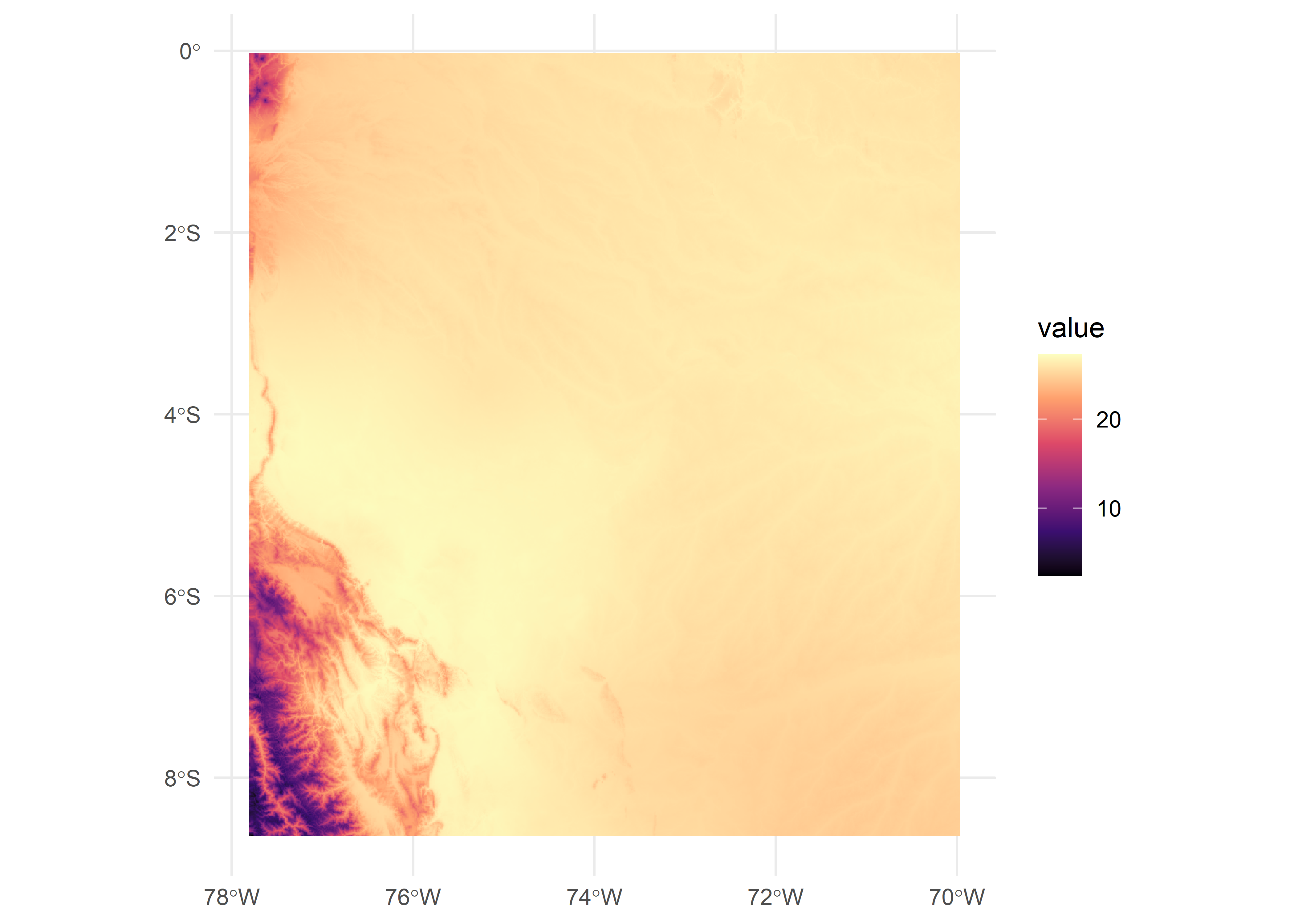

25.4.4.1.2 Enmascaramiento

Podemos utilizar la función mask() para convertir todos los valores fuera del mapa en NA.

# Masking
r <- terra::mask(r, vect(map_2))

ggplot() +
  geom_spatraster(data = r) +
  scale_fill_viridis_c(option = "magma") +
  theme_minimal()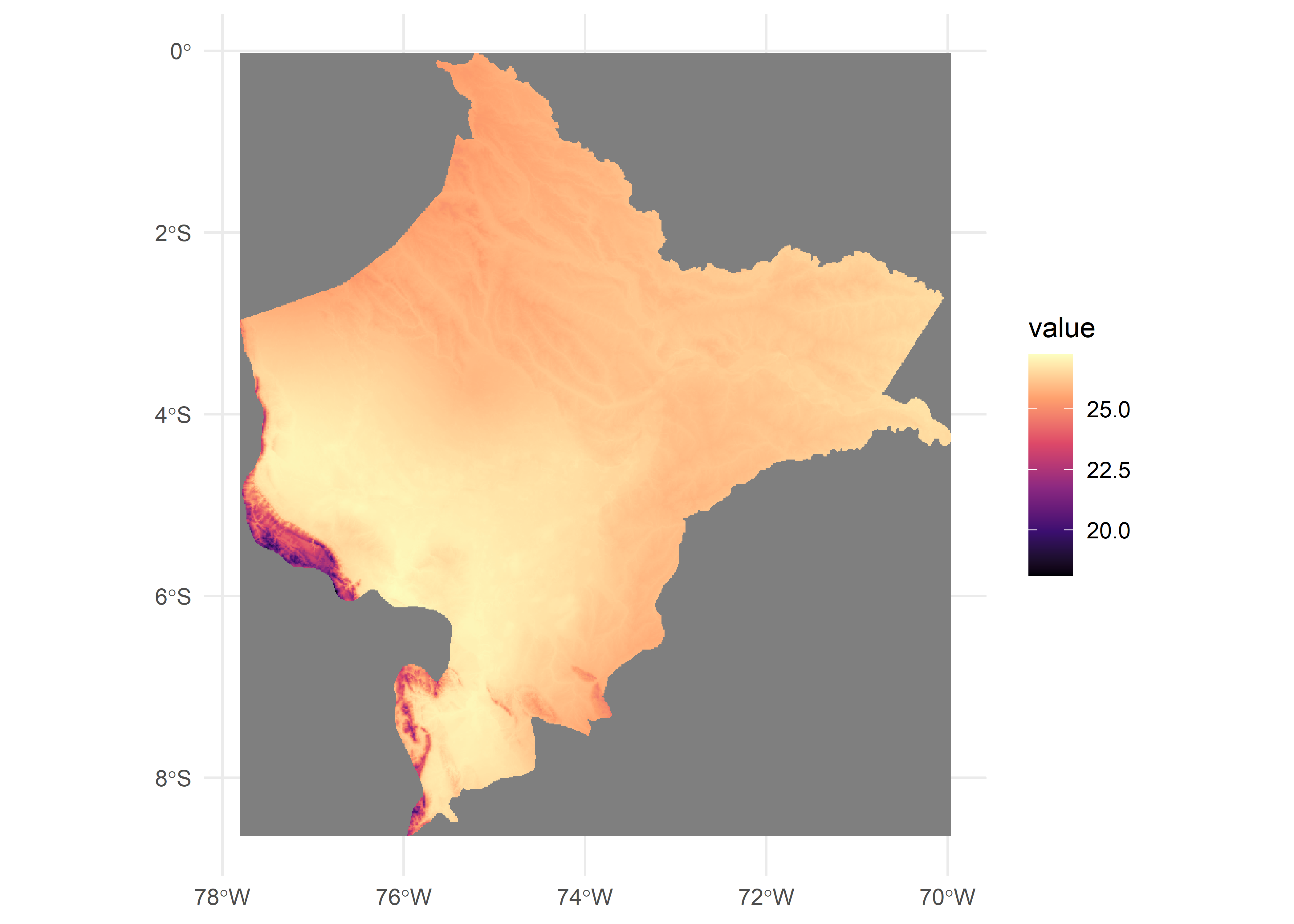

Recorreremos el mapa del departamento de Loreto con la función mapview()

mapview(r, maxpixels = 41558400)

25.4.4.1.3 Agregación

La función aggregate() de terra puede utilizarse para agregar grupos de celdas de un ráster con el fin de crear un nuevo ráster con una resolución menor (es decir, celdas más grandes). El argumento fact de aggregate() denota el factor de agregación expresado como número de celdas en cada dirección (horizontal y vertical), o dos enteros que denotan el factor de agregación horizontal y vertical. El argumento fun especifica la función utilizada para agregar valores (por ejemplo, media). La a continuación muestra un ráster de baja resolución de las temperaturas medias anuales en Perú obtenido mediante la función aggregate().

# Aggregating
r <- terra::aggregate(r, fact = 20, fun = "mean", na.rm = TRUE)

ggplot() +
  geom_spatraster(data = r) +
  scale_fill_viridis_c(option = "magma") +
  theme_minimal()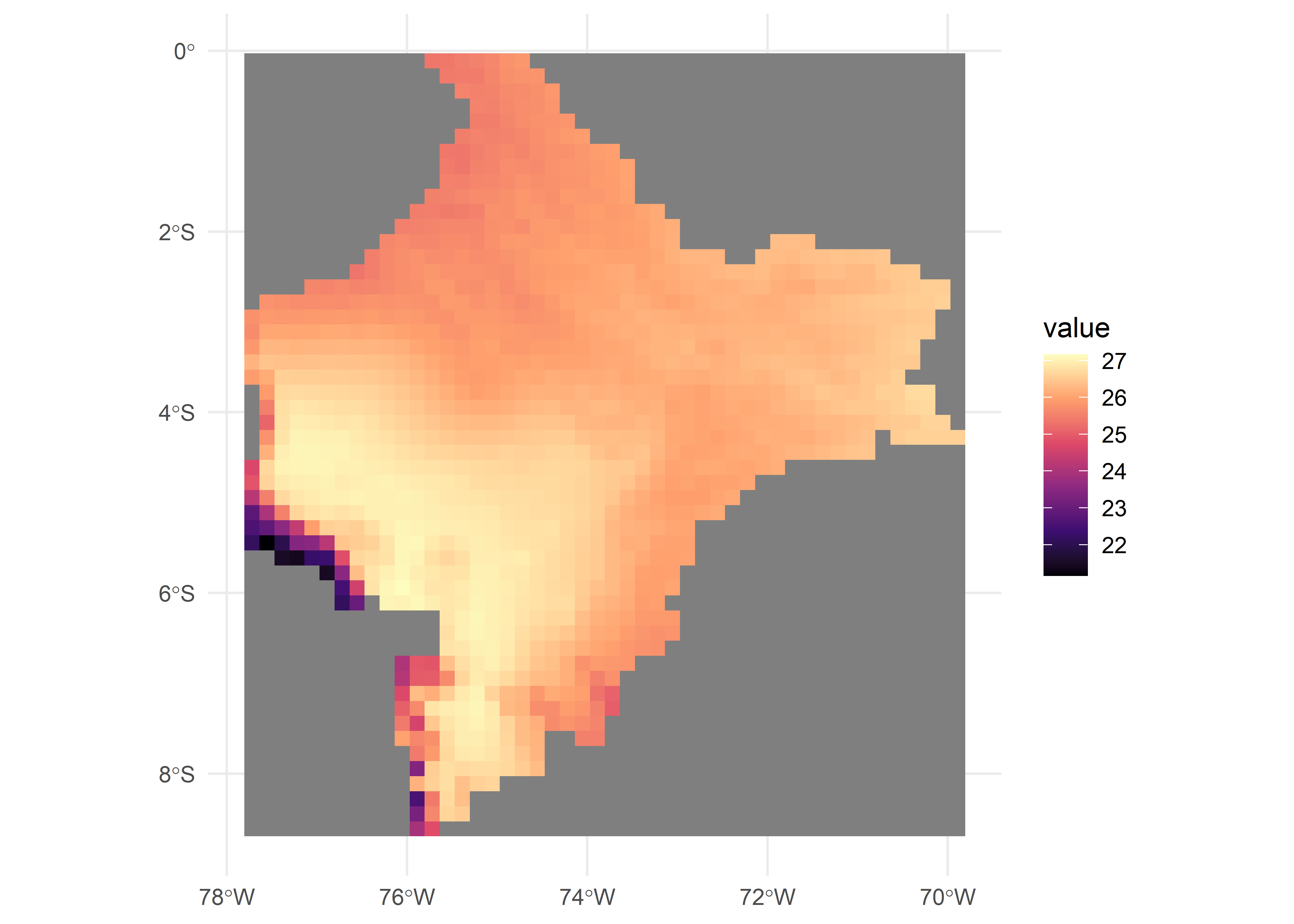

25.5 Análisis Exploratorio de Datos Espaciales

Ahora exploraremos algunas variables de interés en la base de datos para comprender mejor la transmisión de la enfermedad.

25.5.1 Patrones de puntos

Al utilizar la base de datos a nivel individual podemos cambiar las características de nuestra geometría (puntos) de acuerdo a los atributos que deseamos graficar.

Una variable

Usaremos el color de la geometría (argumento col) para representar el sexo de los pacientes con COVID-19 de la base de datos.

covid_p %>%
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  ggplot() +
  geom_sf(aes(col = SEXO), alpha = .2) +
  facet_wrap(.~SEXO)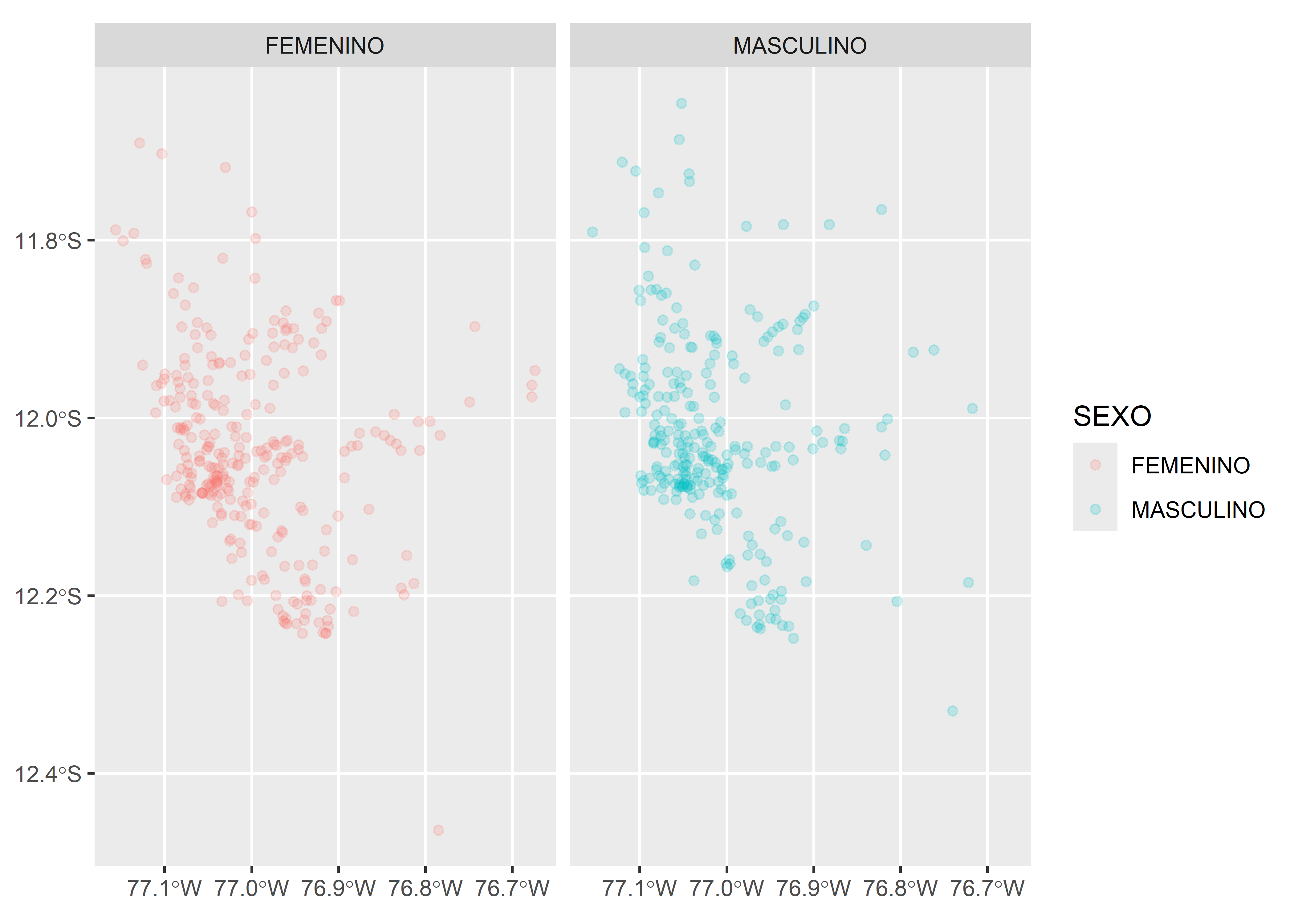

En el caso de la visualización dinámica con mapview, el color se asigna con el argumento zcol.

covid_p %>% 
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  mapview(layer.name = "points", zcol = "SEXO")

Dos o mas variables

Al igual que con los gráficos de datos tabulares, podemos explorar las visualizaciones con facetas y dividir los datos de acuerdo a sub-grupos focalizados.

covid_p %>%
  filter(FECHA_RESULTADO == "2020-04-11" |
         FECHA_RESULTADO == "2020-12-11") %>%
  ggplot() +
  geom_sf(aes(col = SEXO), alpha = .2) +
  facet_grid(SEXO~FECHA_RESULTADO) +
  guides(col = F)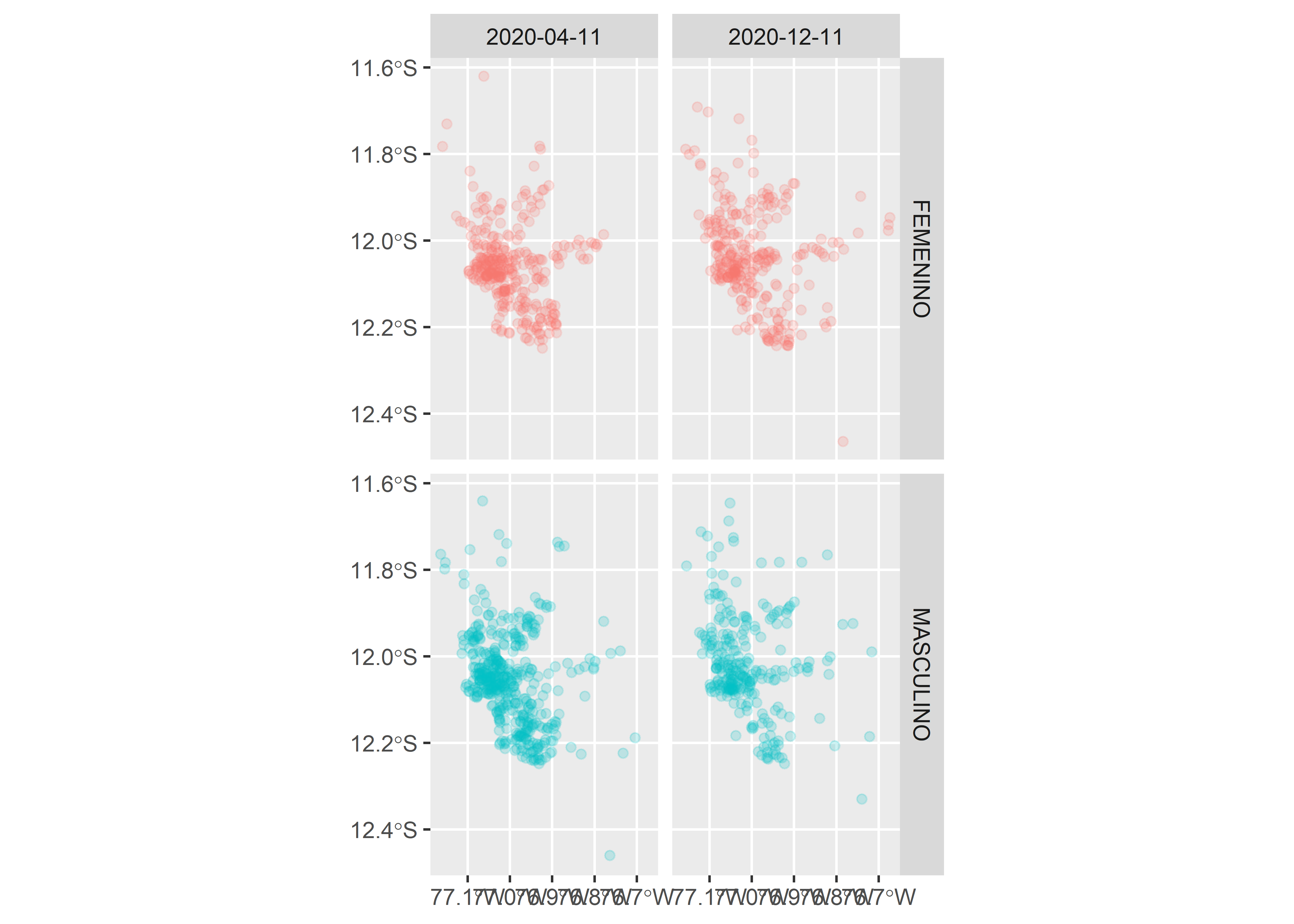

mapview permite agrupar múltiples capas con los operadores + y |. Más detalles en la documentación del paquete.

m1 <- covid_p %>%
  filter(FECHA_RESULTADO == "2020-04-11") %>%
  mapview(zcol = "SEXO")

m2 <- covid_p %>%
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  mapview(zcol = "SEXO")

m1 | m2

Composición

Podemos usar las mismas herramientas usadas para la creación de gráficos de datos tabulares para generar una mejor composición de nuestra representación espacial. Podemos modificar las escalas de color ( scale_color_*() ) y el tema ( theme_*() ), entre otros. Cuando representamos datos espaciales es importante representar la escala espacial de los datos y el norte. Ambas características pueden ser graficadas con el paquete ggspatial.

covid_p %>%
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  ggplot() +
  geom_sf(data = covid_sf) +
  geom_sf(aes(col = EDAD), alpha = .2) +
  scale_color_viridis_c(option = "B") +
  annotation_scale() +
  annotation_north_arrow(location = "tr", style = north_arrow_nautical) +
  theme_bw()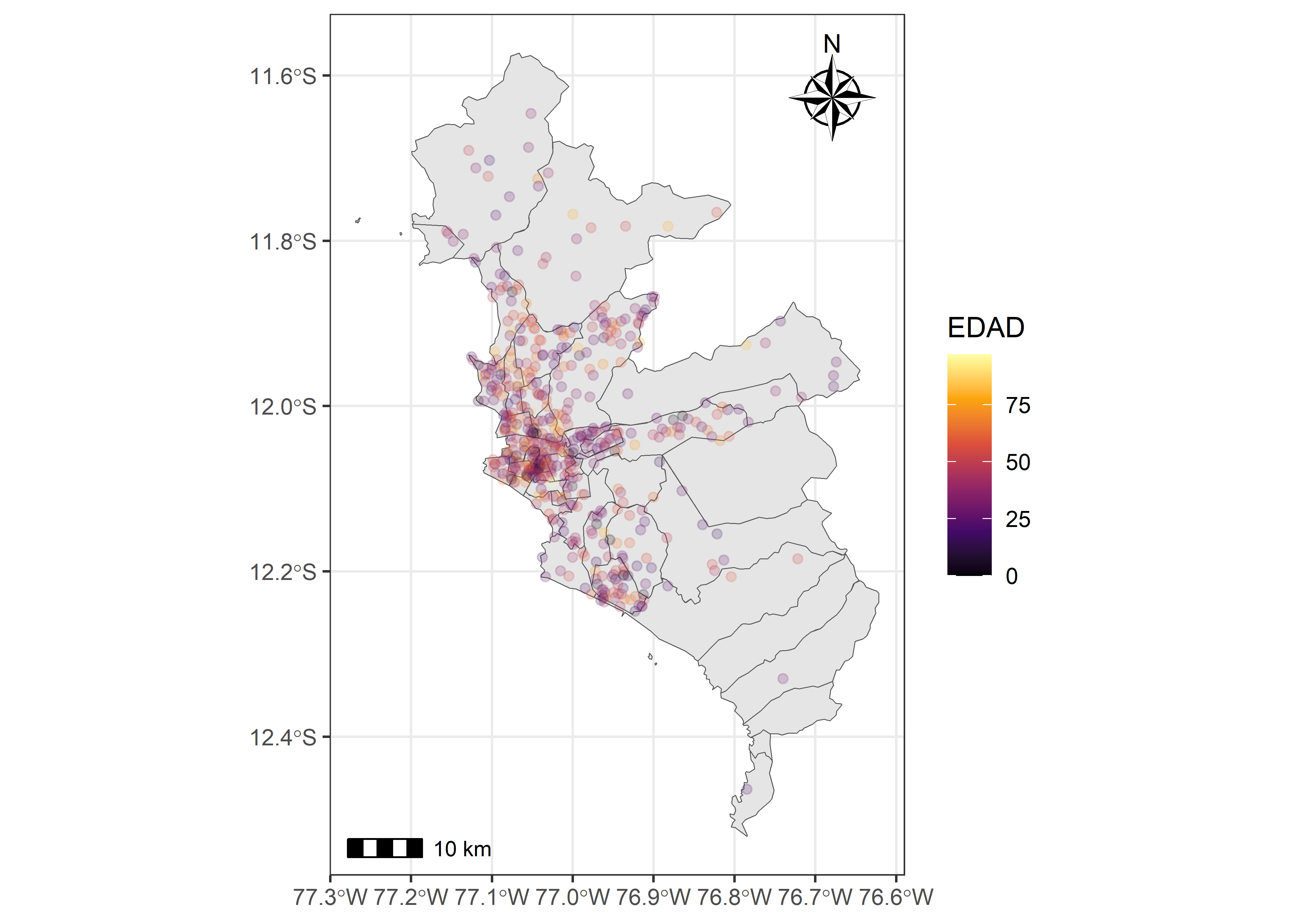

25.5.2 Datos en polígonos

La forma de reporte más común de los sistemas de vigilancia de enfermedades infecciosas es la agrupación de casos por unidades geográficas o administrativas. En esta sección exploraremos la representación de datos en polígonos espaciales.

Una variable

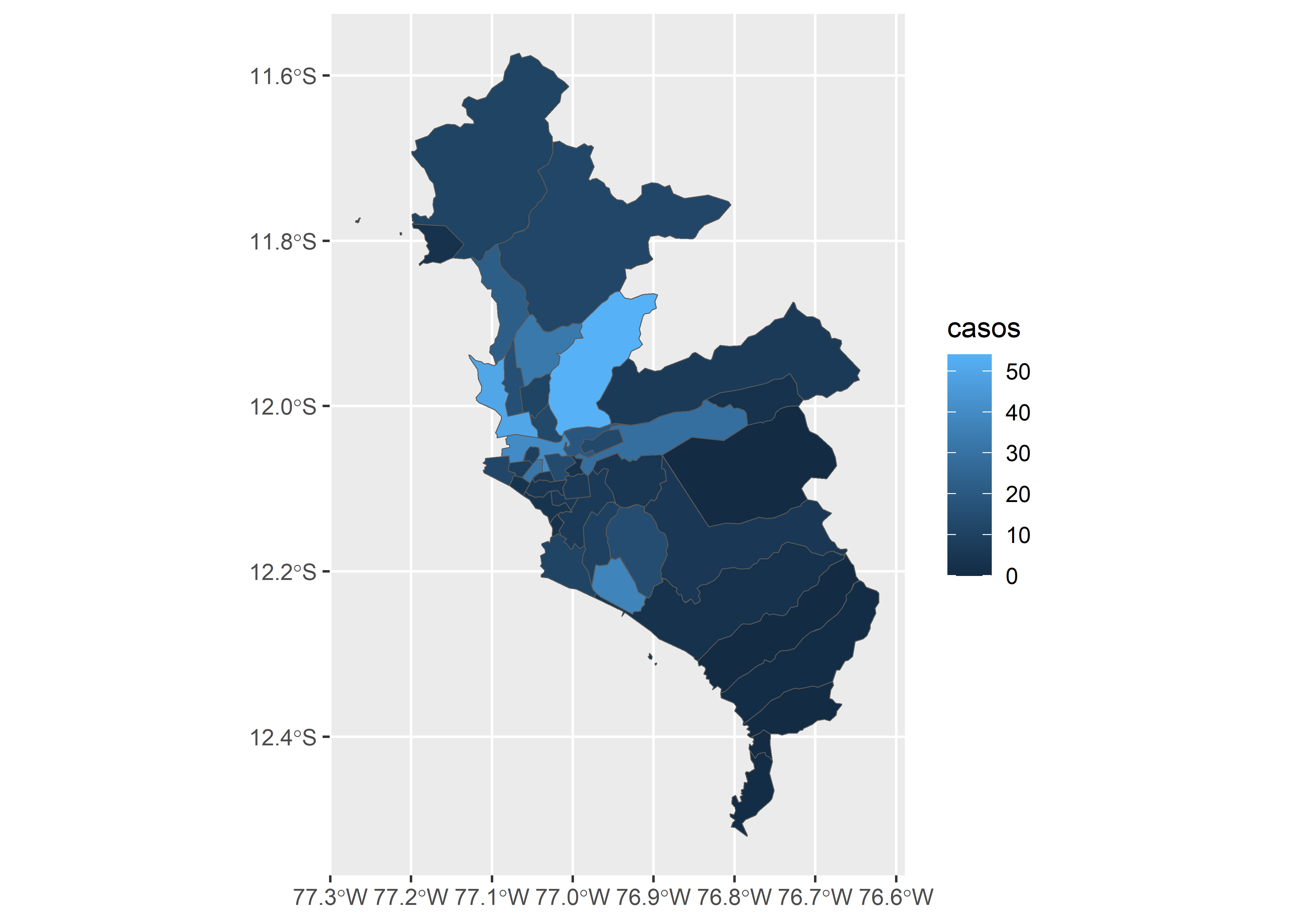
Usaremos el relleno de la geometría (argumento fill) para representar el número de casos de COVID-19 por distritos en Lima metropolitana. Es importante notar que el argumento color (col) se usa para definir el color de los bordes de la geometría.

covid_sf %>%
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  ggplot() +
  geom_sf(aes(fill = casos))

En el caso de la visualización dinámica con mapview, el relleno también se asigna con el argumento zcol.

covid_sf %>% 
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  mapview(layer.name = "casos", zcol = "casos")

Dos o mas variables

Seleccionaremos 2 fechas para comparar la evolución de la epidemia.

covid_sf %>%
  filter(FECHA_RESULTADO == "2020-04-11" |
         FECHA_RESULTADO == "2020-12-11") %>%
  ggplot() +
  geom_sf(aes(fill = casos)) +
  facet_grid(.~FECHA_RESULTADO)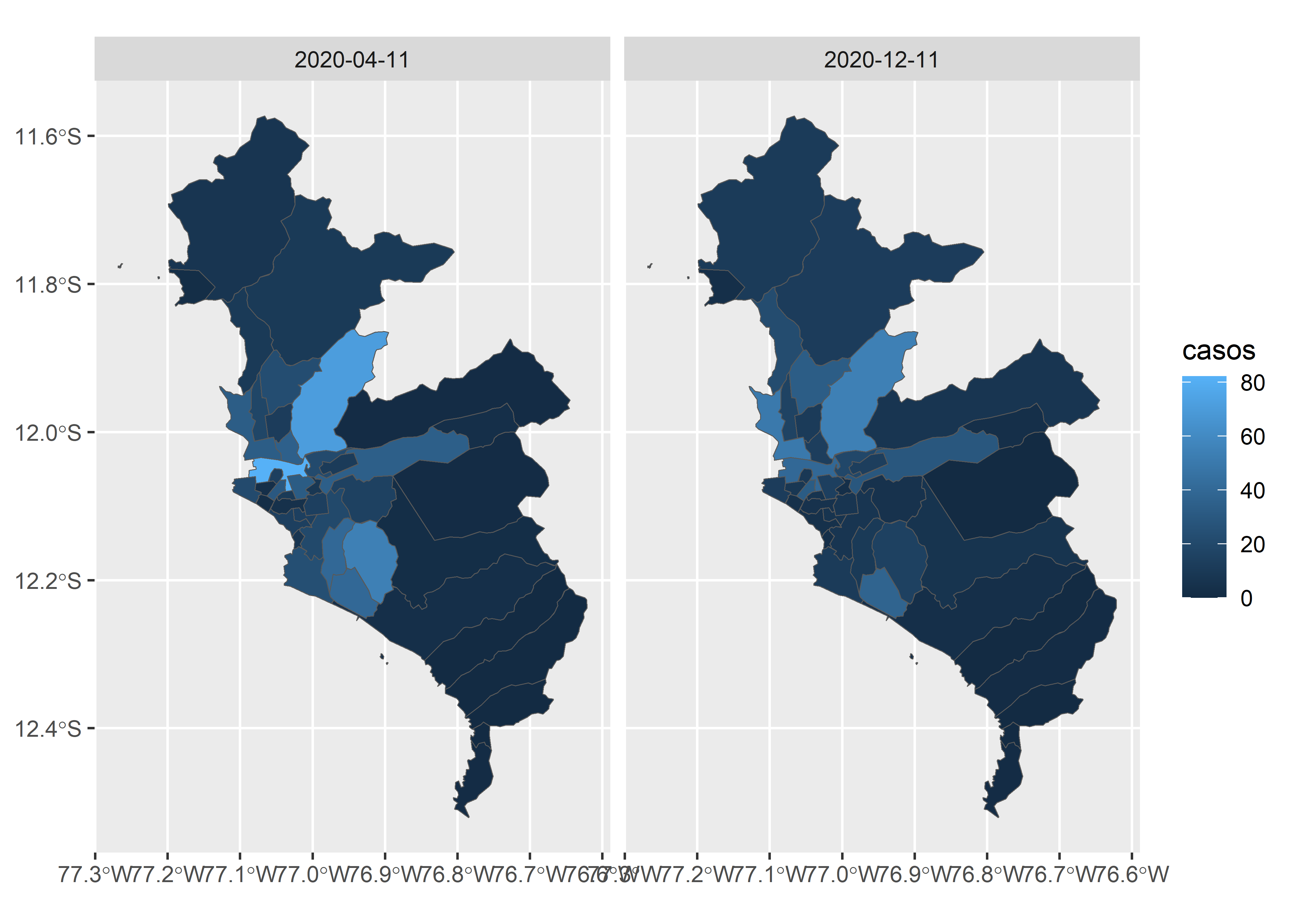

También podemos visualizar la distribución espacial de ambas fechas de forma dinámica.

d1 <- covid_sf %>%
  filter(FECHA_RESULTADO == "2020-04-11") %>%
  mapview(zcol = "casos")

d2 <- covid_sf %>%
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  mapview(zcol = "casos")

d1 | d2

Composición

Al igual que con los datos de puntos, podemos usar las mismas herramientas para generar una mejor composición de nuestra representación espacial.

covid_sf %>%
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  ggplot() +
  geom_sf(aes(fill = casos)) +
  scale_fill_viridis_c(option = "F", direction = -1) +
  annotation_scale() +
  annotation_north_arrow(location = "tr", style = north_arrow_nautical) +
  theme_void()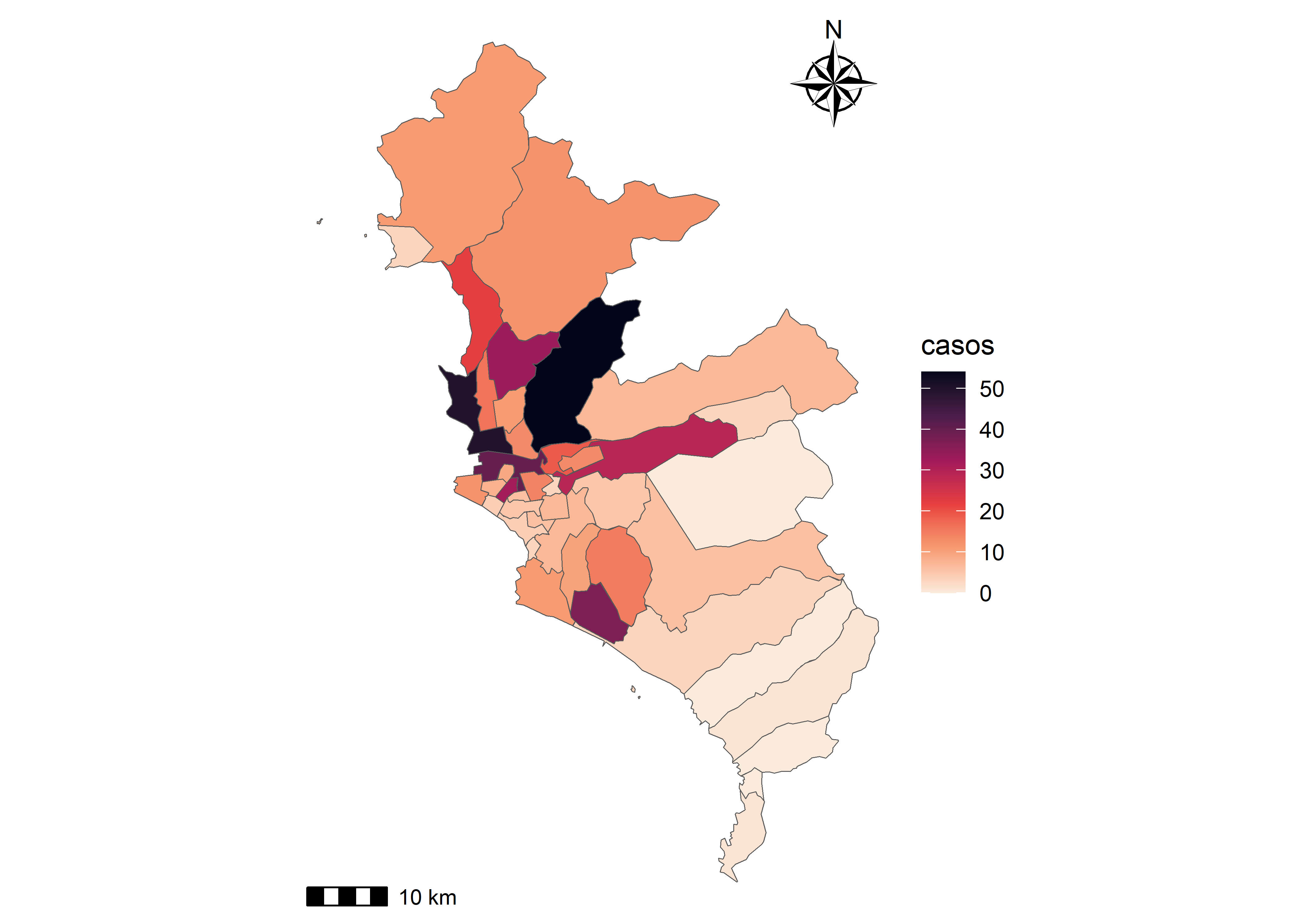

Otro paquete importante de revisar para la representación de estructuras espaciales es: tmap.

25.6 Autocorrelación espacial

Para estos ejemplos usaremos datos agregados en unidades administrativas (polígonos). El procedimiento puede ser modificado para hacer la misma rutina en datos de puntos.

Las pruebas de autocorrelación espacial miden la correlación de una variable en el espacio, es decir, las relaciones con las unidades espaciales cercanas.

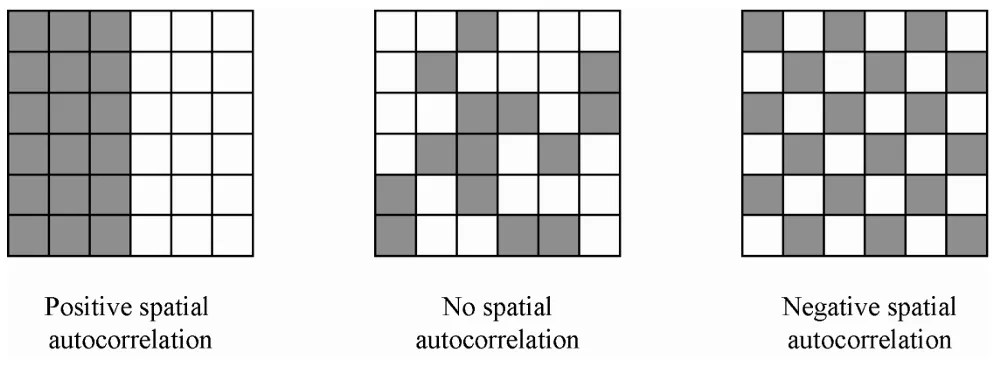
• Una autocorrelación positiva significa que los casos cercanos son similares o están agrupados (Imagen izquierda).
• Una autocorrelación negativa significa que los casos cercanos son diferentes o están dispersos (Imagen derecha).
• No autocorrelación significa que los casos vecinos no tienen una relación particular o son aleatorios (Imagen central).

25.6.1 Autocorrelación Global

Para llevar a cabo el cálculo de estadístico de Moran’s I global, en primer lugar establecemos el conjunto de datos de análisis. Debido a la estructura longitudinal de la base de datos, filtraremos por un rango de fechas en específico (Noviembre 2020).

covid_sf_subset <- covid_sf %>%
  filter(FECHA_RESULTADO >= "2020-11-01", 
         FECHA_RESULTADO <= "2020-11-30") %>%
  group_by(DISTRITO) %>%
  summarise(casos = sum(casos, na.rm = T))

Luego, a partir de la distribución de los polígonos (distritos) en el área de estudio definiremos la matriz de vecindad.

covid_esda <- covid_sf_subset %>%
  mutate(nb = st_contiguity(geometry))

La vecindad se define como todas aquellas unidades espaciales que comparten al menos un borde común. En la siguiente visualización observaremos el vecindario del distrito de Lima.

covid_esda %>%
  ggplot() + 
  geom_sf(fill = "white") + 
  geom_sf(data = covid_esda %>% filter(row_number() %in% nb[[15]]),
          fill = "gray") + 
  geom_sf(data = covid_esda %>% filter(DISTRITO == "LIMA"), 
          fill = "black") +
  scale_fill_manual(values = c("a","b","c")) +
  theme_bw()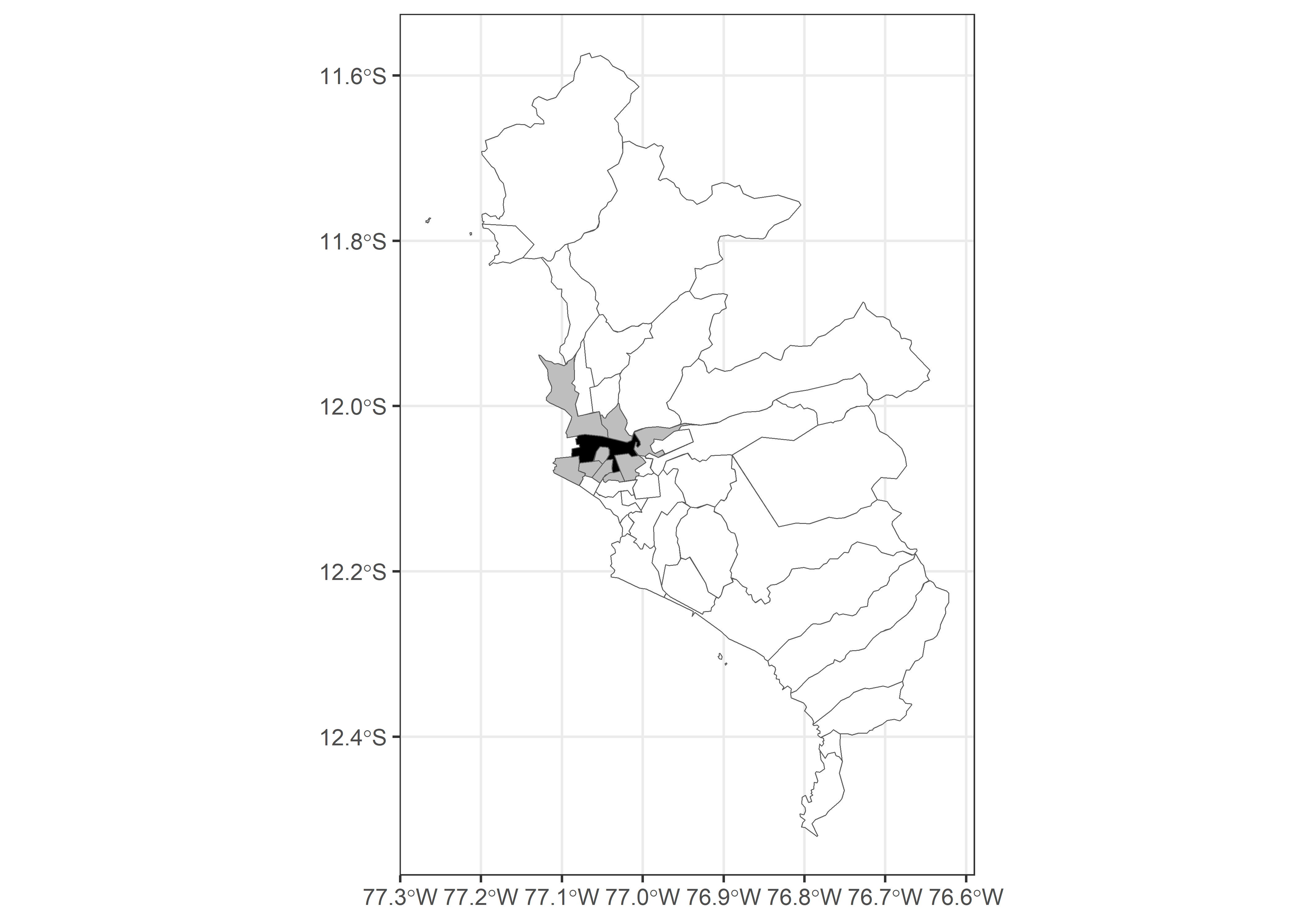

Con la matriz de vecindad llevamos a cabo el cálculo de la matriz de pesos espaciales:

covid_esda <- covid_sf_subset %>%
  mutate(nb = st_contiguity(geometry),
         wt = st_weights(nb))

Ahora, con los pesos espaciales creamos los rezagos espaciales ( “spatial lags” ).

covid_esda <- covid_sf_subset %>%
  mutate(nb = st_contiguity(geometry),
         wt = st_weights(nb),
         casos_lag = st_lag(casos, nb, wt))

Finalmente, realizamos el cálculo de la prueba de Moran global I:

global_moran_test(covid_esda$casos, 
              covid_esda$nb, 
              covid_esda$wt)

    Moran I test under randomisation

data:  x  
weights: listw    

Moran I statistic standard deviate = 2.591, p-value = 0.004785
alternative hypothesis: greater
sample estimates:
Moran I statistic       Expectation          Variance 
       0.25425435       -0.02380952        0.01151737 

Nota: La prueba implementada por defecto utiliza un cálculo analítico del estadístico de Moran I. Esta prueba, sin embargo, es muy susceptible a polígonos distribuidos irregularmente. Por ello actualmente el paquete sfdep cuenta con una versión de la prueba que se basa en simulaciones de Monte Carlo, la cual puede ser llevada a cabo con la función global_moran_perm().

Para una mejor interpretación de esta prueba podemos graficar los valores de las localizaciones índices contra los valores ponderados en los rezagos (lags) espaciales (o vecindarios).

covid_esda %>%
  ggplot(aes(casos, casos_lag)) +
  geom_point() +
  geom_smooth(method="lm", col = "red") + 
  geom_hline(aes(yintercept = mean(casos_lag)), lty = "dashed") + 
  geom_vline(aes(xintercept = mean(casos)), lty = "dashed") + 
  theme_minimal()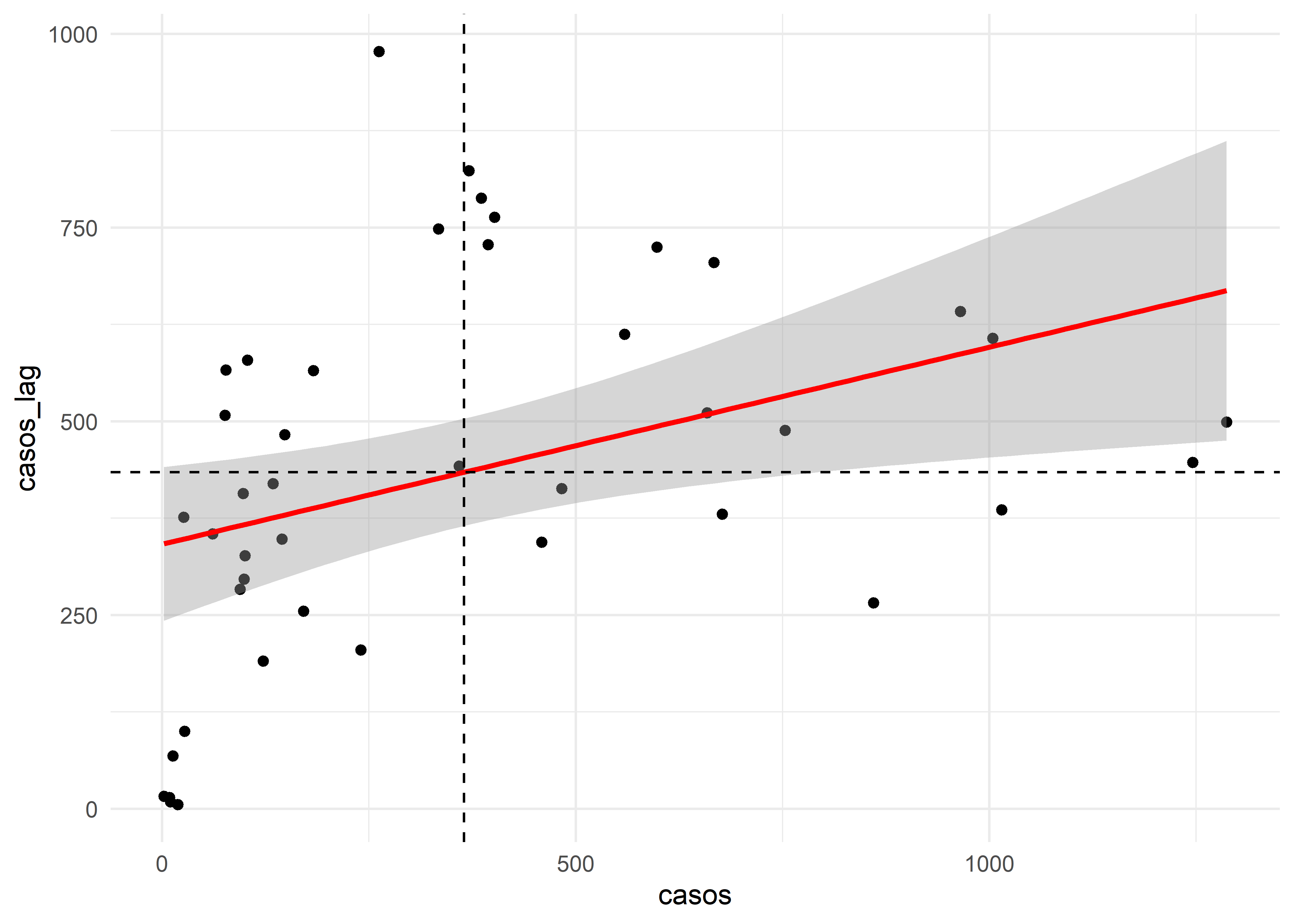

El Moran’s I es positivo y moderado, lo cual significa que existe un grado de agrupación (autocorrelación) espacial de los datos. En el gráfico vemos que existe una mayor distribución de puntos en el cuadrante superior derecho e inferior izquierdo. Esto significa que los valores bajos en las localizaciones indices estan cerca a los valores bajos en sus vecindarios (cuadrante inferior izquierdo) y que los valores altos en las localizaciones indices estan cerca a los valores altos en sus vecindarios (cuadrante superior derecho).

25.6.2 Autocorrelación Local (LISA)

Para el cálculo de la autocorrelación espacial local, en primer lugar establecemos los umbrales (del estadístico z) a partir de los cuales se definen los clústers de valores altos y bajos.

breaks <- c(-Inf, -2.58, -1.96, -1.65, 1.65, 1.96, 2.58, Inf)
labels <- c("Cold spot (significance level = 0.01)",
            "Cold spot (significance level = 0.05)",
            "Cold spot (significance level = 0.10)",
            "Not significant",
            "Hot spot (significance level = 0.10)",
            "Hot spot (significance level = 0.05)",
            "Hot spot (significance level = 0.01)")

25.6.2.1 Moran’s I

Despues de identificar identificar los elementos de los cuatro cuadrantes del gráfico de Moran’s I Global, vamos a realizar una prueba de Moran’s I Local para identificar el patrón de cada unidad espacial y su distribución en el espacio. Usaremos la función local_moran() del paquete sfdep.

covid_lisa <- covid_esda %>%
  mutate(moran = local_moran(casos, nb, wt))

Ahora podemos identificar los 4 patrones.

covid_lisa %>%
  unnest(moran) %>%
  ggplot(aes(casos, casos_lag, col = mean)) +
  geom_point(aes(alpha = abs(z_ii),
                 size = abs(z_ii))) +
  geom_smooth(method="lm", col = "red") + 
  geom_hline(aes(yintercept = mean(casos_lag)), lty = "dashed") + 
  geom_vline(aes(xintercept = mean(casos)), lty = "dashed") + 
  theme_minimal()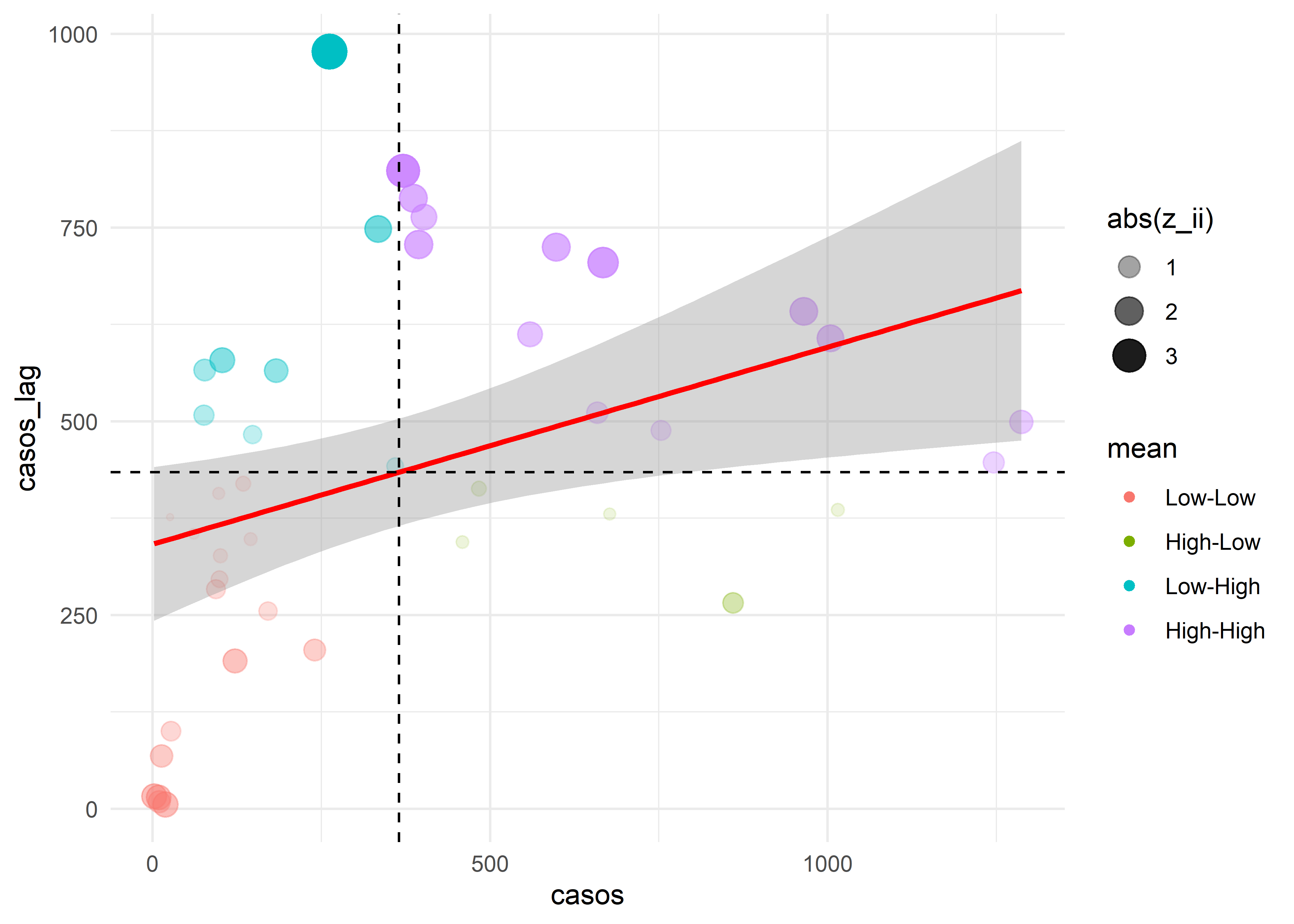

Ahora exploraremos su distribución en el espacio.

covid_lisa %>% 
  unnest(moran) %>% 
  mutate(pysal = ifelse(p_folded_sim <= 0.1, as.character(pysal), NA)) %>%
  ggplot(aes(fill = pysal)) +
  geom_sf(col = "black") +
  theme_bw()

25.6.2.2 Getis Ord Gi*

Realizamos el cálculo del estadístico de Getis Ord usando la función local_gstar() del paquete sfdep.

covid_esda2 <- covid_sf_subset %>%
  mutate(nb2 = include_self(st_contiguity(geometry)),
         wt2 = st_weights(nb2))

covid_lisa2 <- covid_esda2 %>%
  mutate(g = local_gstar(casos, nb2, wt2))

covid_lisa2 <- covid_lisa2 %>%
  mutate(cluster_g = cut(g, include.lowest = TRUE,
                         breaks = breaks,
                         labels = labels))                 

Finalmente, creamos el gráfico:

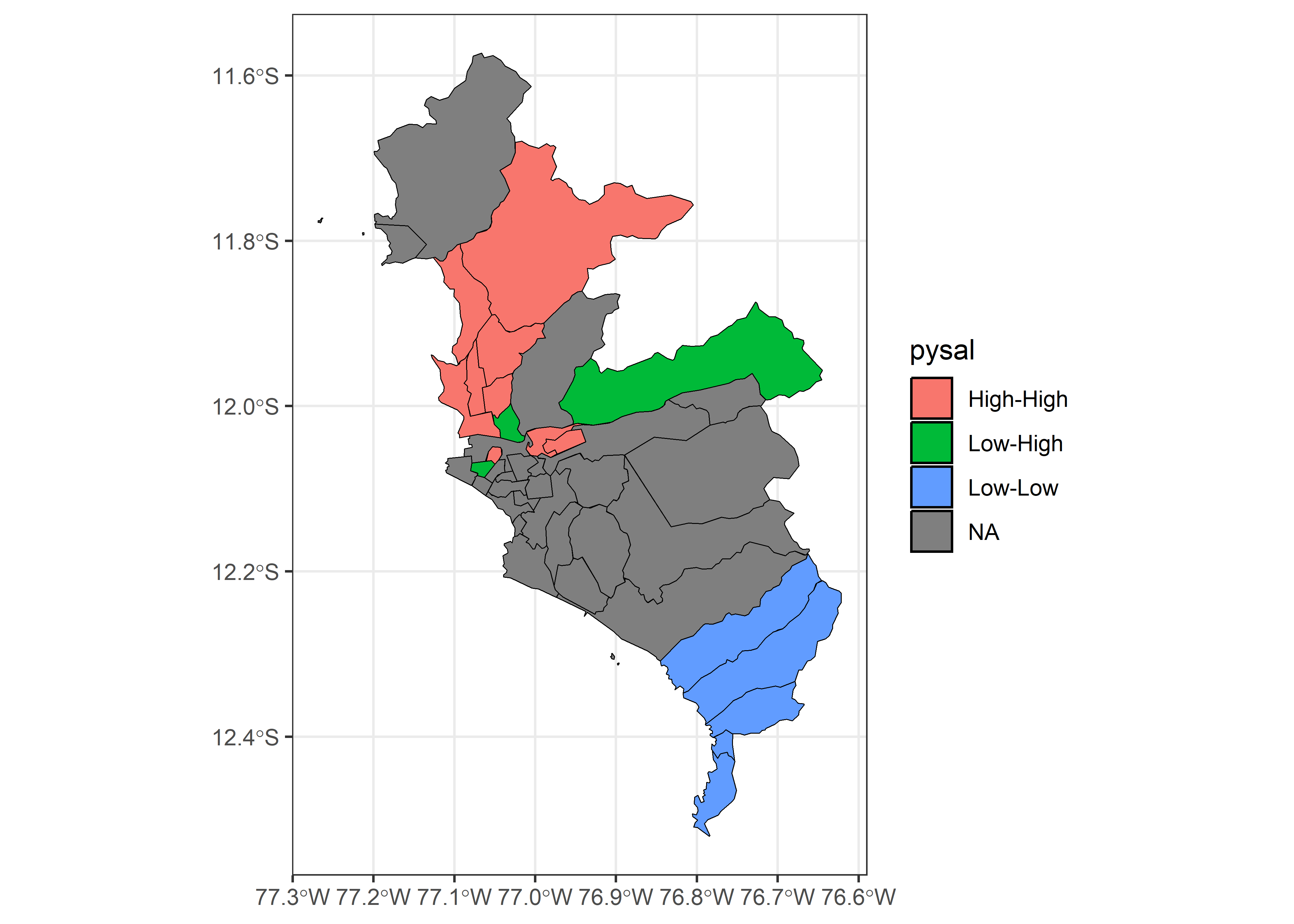
covid_lisa2 %>% 
  ggplot() + 
  geom_sf(aes(fill = cluster_g), show.legend = TRUE) +
  scale_fill_brewer(name="Clúster", 
                    palette = "RdBu", direction = -1, drop = FALSE) +
  theme_bw()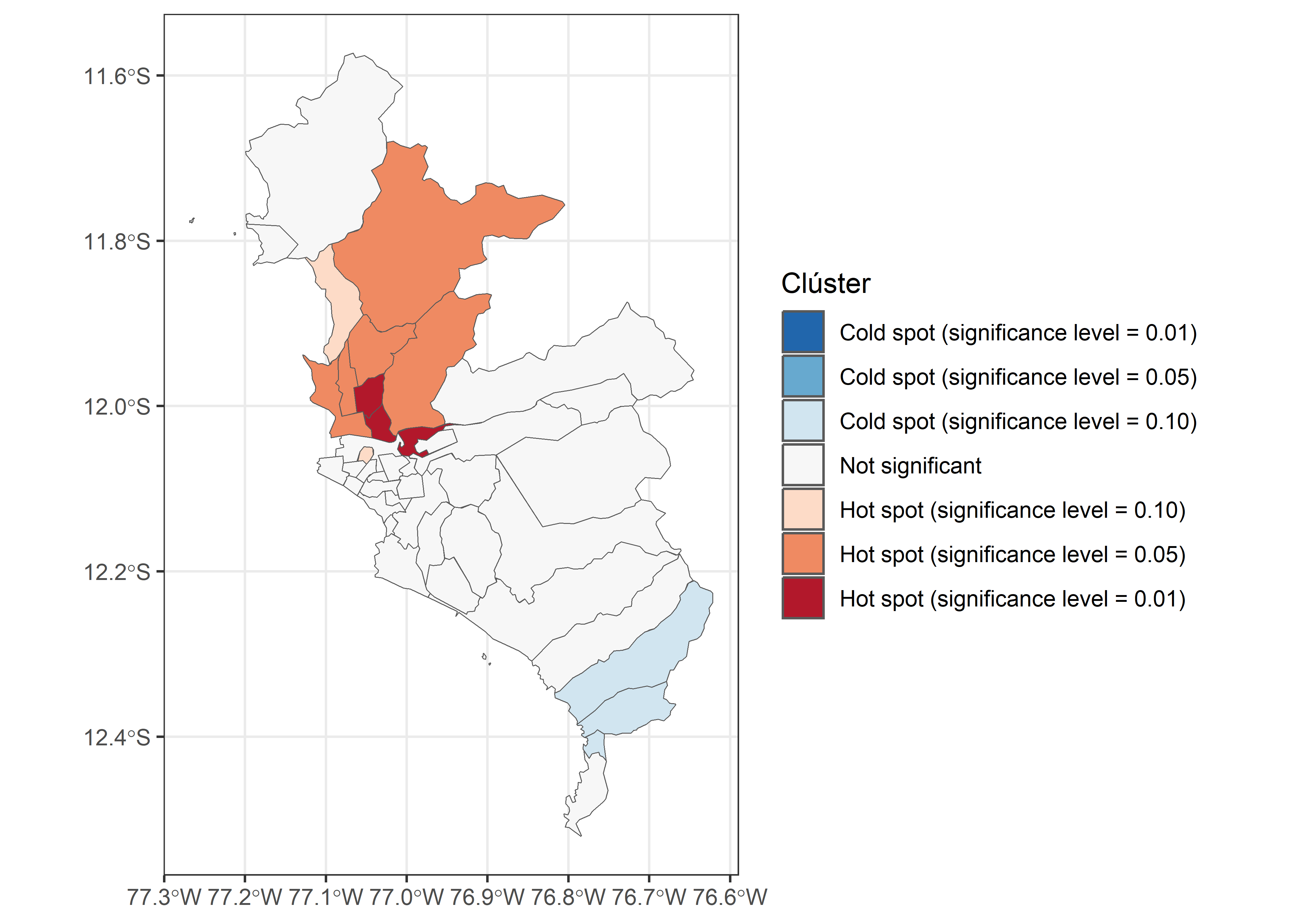

Se puede visualizar clústers espaciales de alta concentración de casos en la zona norte de Lima.

Otro paquete recomendado para hacer análisis de autocorrelación espacial y otras rutinas de análisis espacial es rgeoda que se basa en el software GeoDA.

25.7 Variación espacial de la ocurrencia

En esta sección se brindará una introducción a una metodología para obtener representaciones gráficas de procesos espaciales como el riesgo de una enfermedad. En esta sección exploraremos la estimación de la densidad kernel para datos espaciales que representan procesos discretos (ej. brotes). Existen otras técnicas para datos espaciales que representan procesos continuos (ej. precipitación) como Kriging.

covid_subset <- covid %>%
  filter(FECHA_RESULTADO == "2020-12-11")

m1 <- covid_subset %>%
  st_as_sf(coords = c("lon", "lat"), crs = 4326) %>%
  mapview(layer.name = "points")

m1

Para estimar la densidad del kernel definiremos una ventana espacial de análisis usando la función owin del paquete spatstat.

covid_win <- owin(xrange = range(covid_subset$lon),
                  yrange = range(covid_subset$lat))

Luego, definiremos el objeto patrón de puntos (ppp) a partir de los registros de casos.

covid_ppp  <-  ppp(covid_subset$lon, 
                   covid_subset$lat, 
                   window = covid_win)

Finalmente, el objeto de la clase densidad lo convertiremos a uno de clase rasterLayer. Eliminaremos las áreas fuera de nuestra zona de estudio usando la función mask y utilizando nuestro objeto espacial de los límites de Lima metropolitana (lima_sf).

densidad_raster_cov <- raster(density(covid_ppp, bw.ppl)) %>%
  mask(lima_sf)

Por último, asignamos la proyección correcta de nuestro raster.

projection(densidad_raster_cov) <- CRS("+init=EPSG:4326")

La densidad puede ser representada de la siguiente forma:

m2 <- densidad_raster_cov %>%
  mapview(layer.name = "raster")

m2 + m1

25.7.1 Interpolación espacial

La interpolación espacial es una técnica utilizada en la geografía para estimar valores de variables, espacialmente continuas, en ubicaciones donde no se han tomado mediciones directas, a partir de valores conocidos en puntos cercanos. Esta técnica se basa en la premisa de que los puntos más cercanos tienen valores más similares que los más distantes (Primera ley de Tobler).

Dentro de los métodos para realizar interpolaciones espaciales tenemos los siguientes,

• Análisis de superficie de tendencia: método de interpolación polinómica global que es usado para producir una superficie suave que represente una tendencia gradual sobre el área de interés.

• Distancia inversa ponderada: método de interpolación que estima valores de celdas promediando los valores de puntos de datos de muestra en el vecindario de cada celda de procesamiento.

• Interpolación polinómica: método que utiliza polinomios para estimar valores en ubicaciones donde no se han tomado mediciones directas.

• Kriging: Esta técnica utiliza procedimientos geoestadísticos para generar una superficie estimada a partir de un conjunto disperso de puntos con valores z.

• Interpolación de vecinos naturales: La interpolación de vecino natural encuentra el subconjunto más cercano de muestras de entrada a un punto de consulta y les aplica pesos basados en áreas proporcionales para interpolar un valor.

• Interpolación spline: Este método estima valores utilizando una función matemática que minimiza la curvatura total de la superficie.

25.7.1.1 Kriging

Esta sección estará enfocada en el método de kriging para realizar la interpolación espacial. Recordemos que esta técnica avanzada consiste en utilizar métodos estadísticos para estimar valores desconocidos en ubicaciones no muestreadas, considerando la distancia y la variabilidad entre los puntos de datos. Es importante tener en cuenta que esta técnica solo puede ser utilizada con datos continuos.

Para este ejercicio, se utilizará una base de datos que contiene las incidencias de malaria a nivel de centro poblado en la provincia de Maynas del departamento de Loreto para el año 2022.

malaria_incidence <- st_read("data/malaria_incidence.gpkg",
                             layer = "incidencia_pfalciparum_1000hab_maynas")

Reading layer `incidencia_pfalciparum_1000hab_maynas' from data source 
  `D:\Github\r4pubh\data\malaria_incidence.gpkg' using driver `GPKG'
Simple feature collection with 610 features and 7 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: 432949.5 ymin: 9494089 xmax: 819741.2 ymax: 9904089
Projected CRS: WGS 84 / UTM zone 18S

Posteriormente, se cargará la grilla del área de estudio, la cual tiene una resolución de 5km2 por pixel.

malaria_grid <- st_read("data/malaria_incidence.gpkg",
                     layer = "grilla_regular_maynas_5km")

Reading layer `grilla_regular_maynas_5km' from data source 
  `D:\Github\r4pubh\data\malaria_incidence.gpkg' using driver `GPKG'
Simple feature collection with 3239 features and 7 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 413119.2 ymin: 9479153 xmax: 820324.8 ymax: 9929330
Projected CRS: WGS 84 / UTM zone 18S

A continuación, se visualizarán los dos objetos cargados en nuestro environment utilizando la función mapview.

m1 <- mapview(malaria_incidence, zcol = "INCIDENCI_MALARIA", layer.name = "Malaria Incidence")

m2 <- mapview(malaria_grid, zcol = NULL, layer.name = "grid")

m1 + m2

25.7.1.1.1 Kriging Ordinario

El kriging ordinario es una técnica de interpolación espacial que solo considera la variable de interés teniendo en cuenta su posición. Es importante tomar en cuenta el modelo de ajuste del semivariograma y que la distribución de la variable tiene que aproximarse a la normalidad.

A continuación, se evaluará la distribución de la variable de interés malaria_incidence.

malaria_incidence %>% 
  ggplot(aes(INCIDENCI_MALARIA)) +
  geom_histogram() +
  labs(x = "Incidencia de malaria - Maynas 2022") +
  theme_minimal()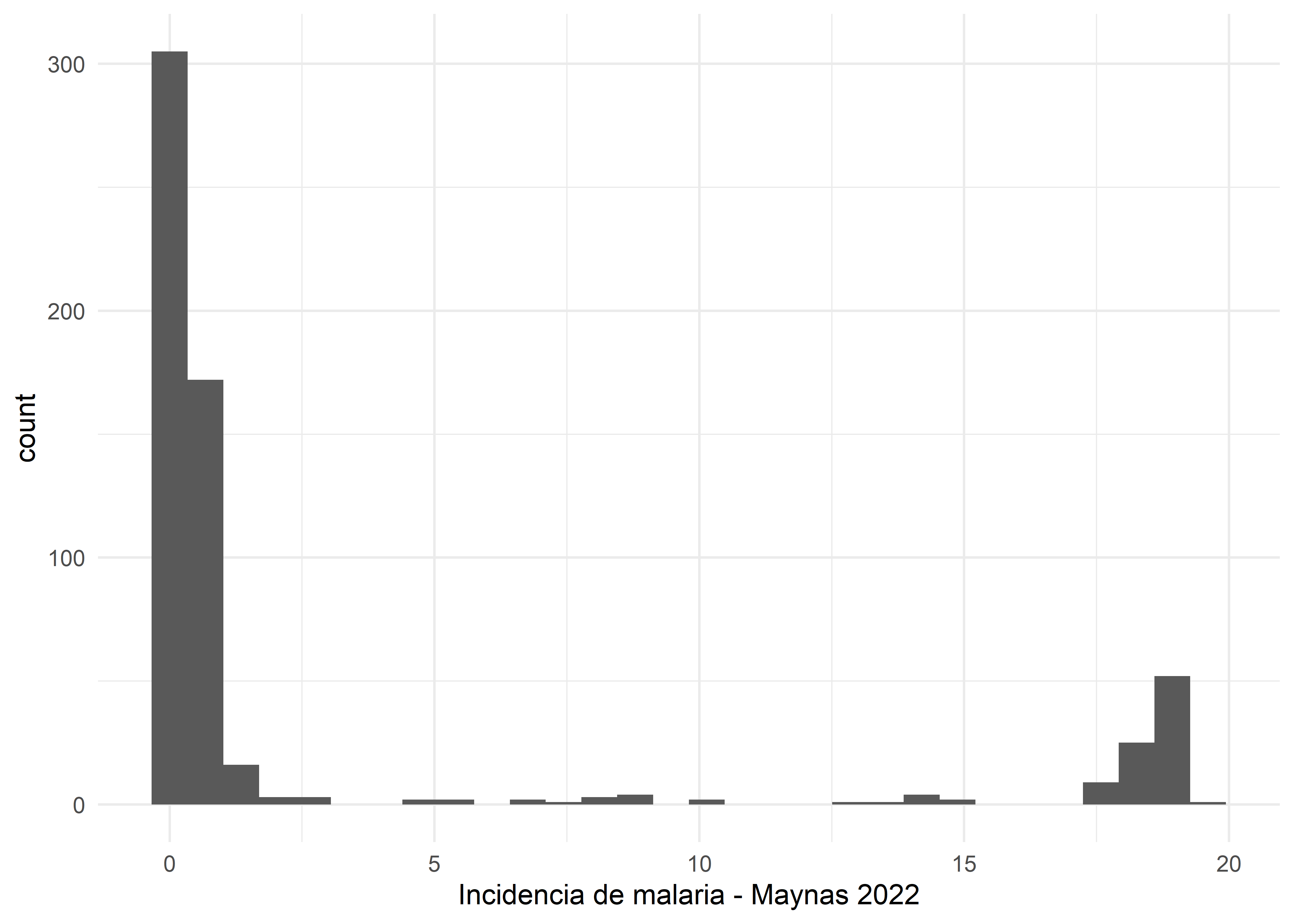

La distribución de la incidencia de malaria, visualmente, no parece acercarse a la normalidad, por lo que deberemos transformarla usando logaritmos.

malaria_incidence_log <- malaria_incidence %>% 
  mutate(incidence_log = log(INCIDENCI_MALARIA))

Una vez transformada la variable, se realizará el semivariograma. Para ello, utilizaremos la función variogram() del paquete gstat.

25.7.1.1.2 Semivariograma

Es una función de estructura que permite estudiar el fenómeno de correlación espacial en función de la distancia (Legendre & Fortin, 1989). En el eje de ordenadas se representa la semivarianza, y en las abscisas la distancia. Donde los pares de puntos mas próximos tienen menos variabilidad que los puntos más lejanos.

\[ \gamma(h) = \frac{1}{2N(h)} \sum_{i=1}^{N(h)} [Z(x_i) - Z(x_i + h)]^2 \]

donde:

• ( (h) ) es el semivariograma para el intervalo de distancia ( h ).
• ( N(h) ) es el número de pares de puntos separados por la distancia ( h ).
• ( Z(x_i) ) es el valor de la variable en el punto ( x_i ).
• ( Z(x_i + h) ) es el valor de la variable en el punto separado por la distancia ( h ) desde ( x_i ).

Existen dos tipos de semivariogramas: el experimental (o empírico) y el teórico. El experimental, es aquel obtenido de nuestros propios datos, mientras que el teórico es la función matemática que se ajusta al semivariograma empírico.

Ahora, se calculará el semivariograma empírico,

semivariograma <- variogram(
  object = malaria_incidence_log$incidence_log ~ 1,
  data = malaria_incidence_log,
  locations = st_centroid(malaria_grid),
  cutoff = 100*100)

plot(semivariograma)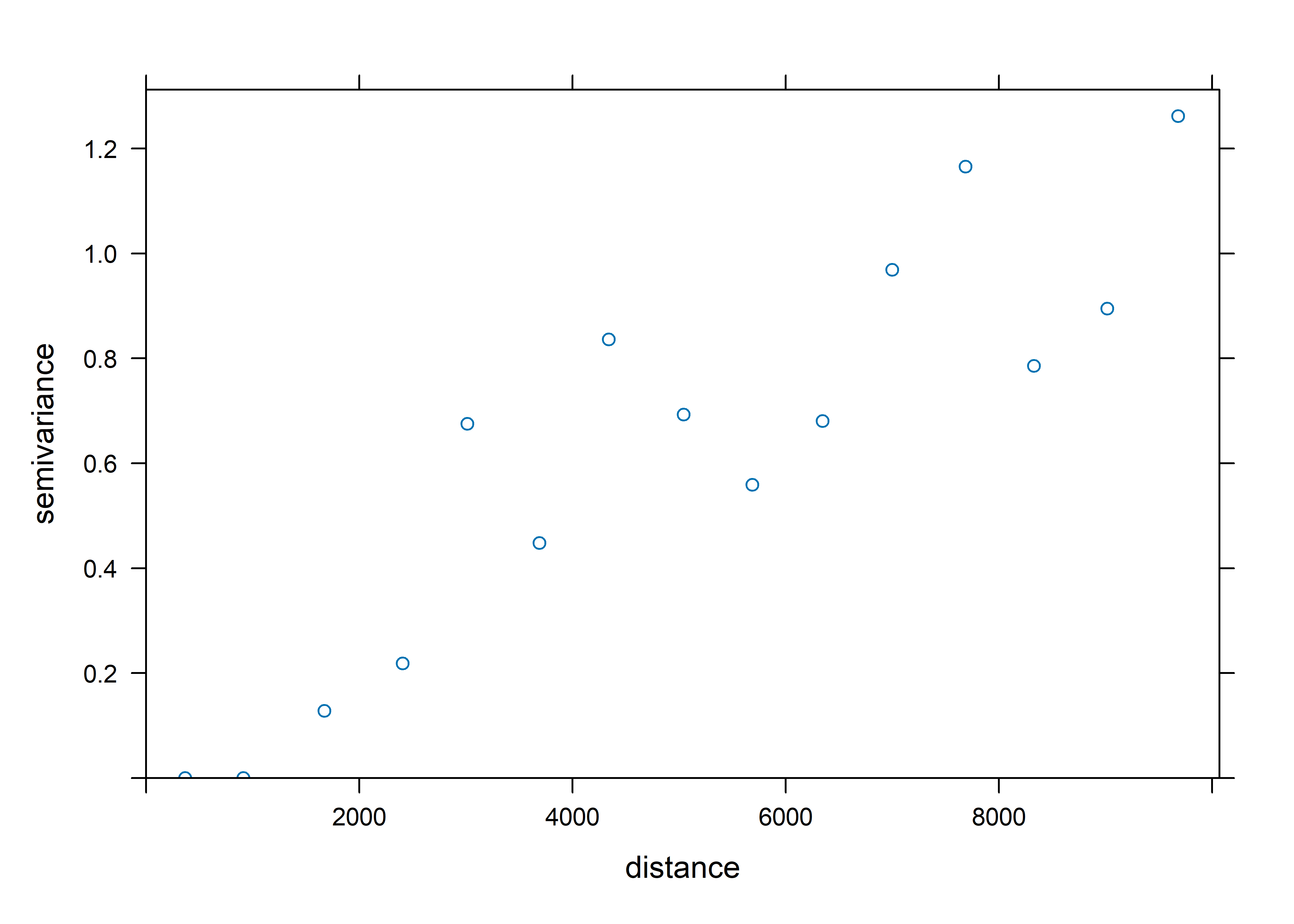

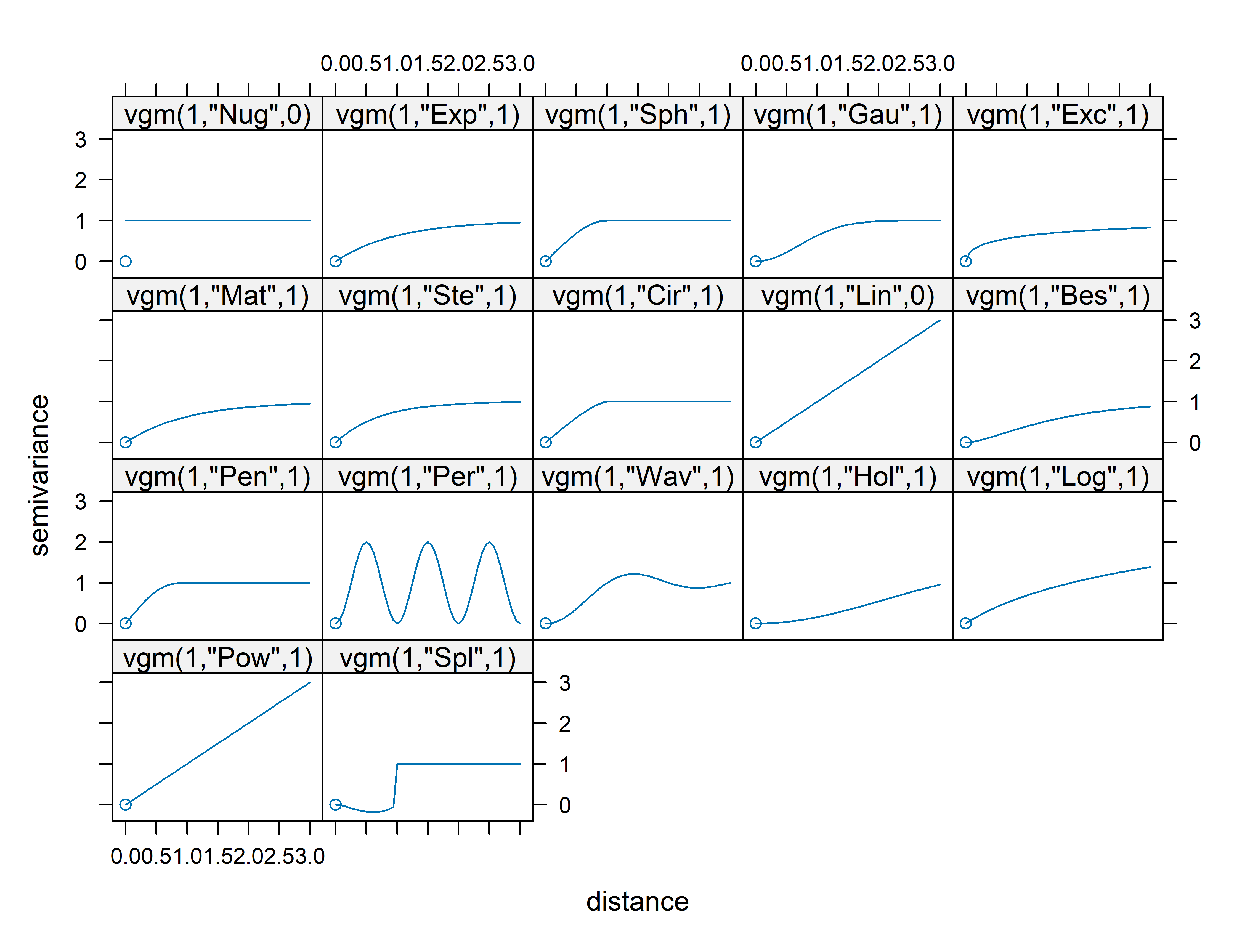
Podemos acceder a los semivariogramas teóricos con la función show.vgms() del paquete gstat.

show.vgms()

A continuación, ajustaremos el semivariograma con el mejor modelo teórico. Para ello, utilizaremos la función fit.variogram() y especificaremos cuáles son los modelos que se tienen que evaluar.

model_semivariograma <- fit.variogram(
  object = semivariograma,
  model = vgm(c("Exp","Sph","Gau","Lin")))

model_semivariograma

  model     psill    range
1   Nug 0.0000000    0.000
2   Gau 0.9376012 3817.428

Del resultado anterior, se puede concluir que el mejor modelo para ajustar el semivariograma es el modelo Gaussiano.

Ahora, se visualizará tanto el modelo empírico como el teórico.

plot(semivariograma,model_semivariograma)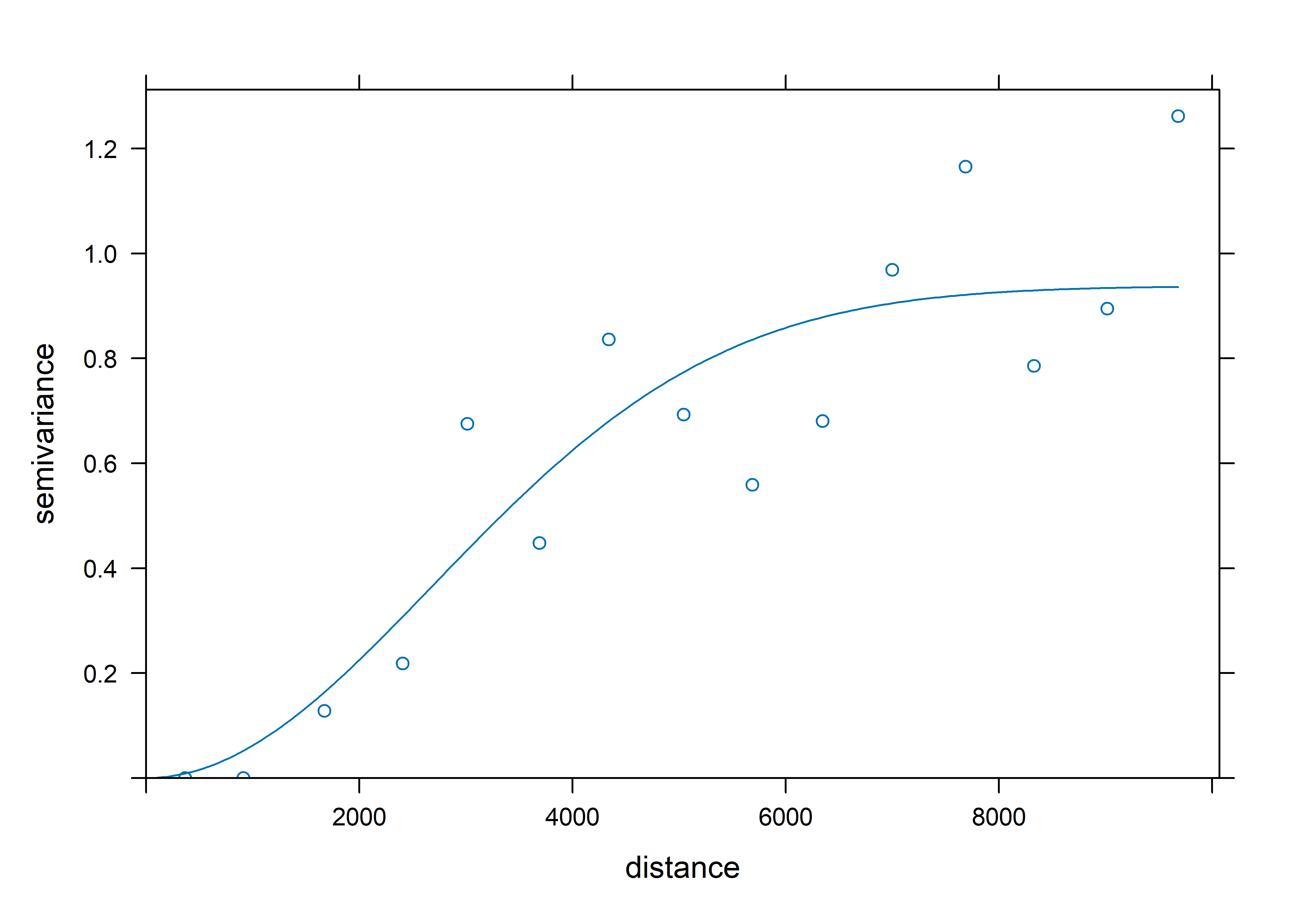

Una vez ajustado nuestro modelo, se procederá a realizar la estimación de valores en todas las grillas con la función krige() del paquete gstat.

kriging <- krige(
  incidence_log ~ 1,
  malaria_incidence_log,
  st_centroid(malaria_grid),
  model_semivariograma)

[using ordinary kriging]

head(kriging)

Simple feature collection with 6 features and 2 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: 414384.9 ymin: 9791323 xmax: 419392.1 ymax: 9807934
Projected CRS: WGS 84 / UTM zone 18S
   var1.pred  var1.var                 geometry
1 -0.9795884 0.9396279 POINT (414751.2 9802483)
2 -0.9795884 0.9396279 POINT (414384.9 9798967)
3 -0.9795884 0.9396279 POINT (414589.4 9794625)
4 -0.9795884 0.9396279 POINT (415318.5 9791323)
5 -0.9795894 0.9396279 POINT (419392.1 9807934)
6 -0.9795884 0.9396279 POINT (418125.1 9803929)

Las variable var1.pred son los valores predichos, mientras que la varibale var1.var es la varianza que permite cuantificar la incertidumbre de la predicción.

Ahora procederemos a visualizar de forma espacial los resultados. Para ello, vamos a agregar estas variables a nuestras grillas.

malaria_grid_pred_log <- malaria_grid %>% 
  mutate(
    var = kriging$var1.var,
    predicted = kriging$var1.pred
  )

Ahora se realizarán los mapas,

p1 <- malaria_grid_pred_log %>% 
  ggplot() +
  geom_sf(aes(fill = predicted), color = NA) +
  scale_fill_viridis_c() +
  labs(fill = "Incidencia Estimada") +
  theme_bw()

p2 <- malaria_grid_pred_log %>% 
  ggplot() +
  geom_sf(aes(fill = var), color = NA) +
  scale_fill_viridis_c() +
  labs(fill = "Varianza") +
  theme_bw()

p1 | p2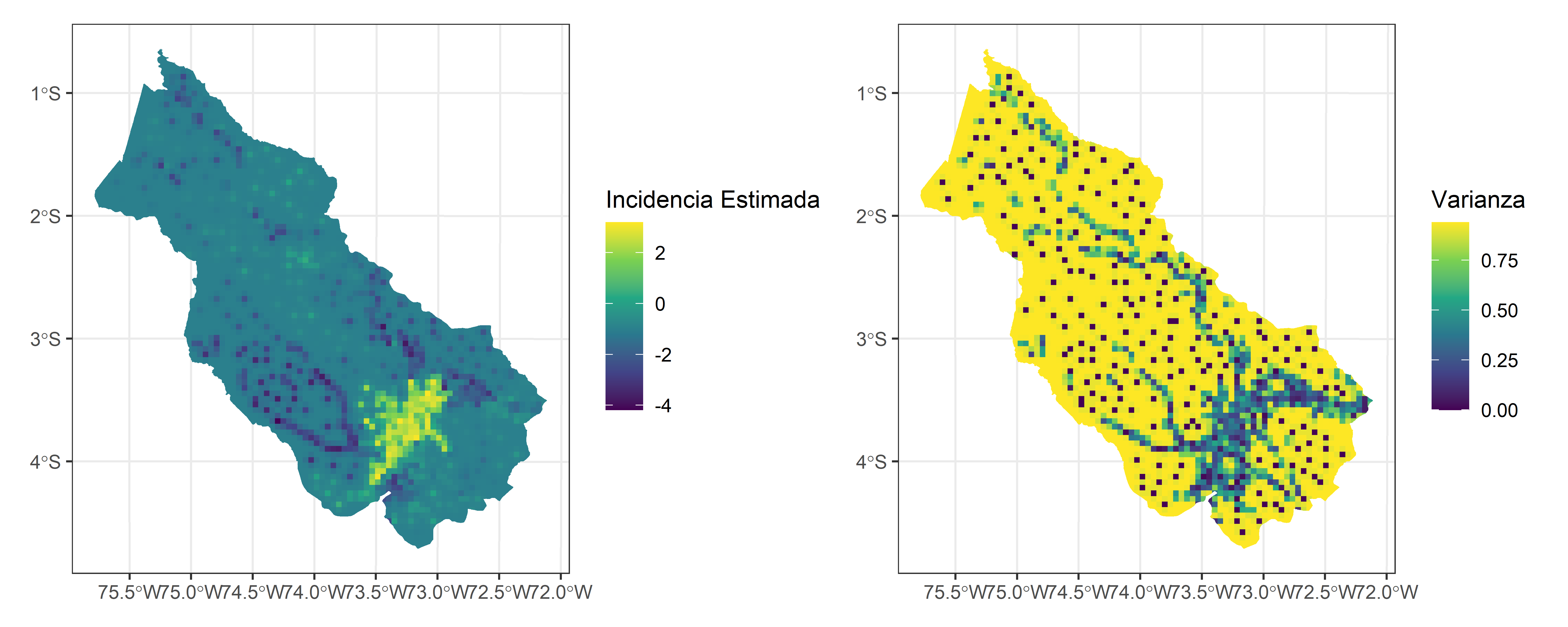

25.8 Análisis de Agrupamiento Espacial

25.8.1 Estadísticas de escaneo espacial (SSS)

Para realizar el cálculo de las estadísticas de escaneo espacial (o Spatial Scan Statistics - SSS), primero es necesario emplear datos de la clase patrones de puntos o ppp :

En este ejemplo, para definir una variable binaria, usaremos los casos detectados por PCR como infecciones recientes (positivo) y por otros métodos (ej. Prueba de Anticuerpos - PR) como infecciones pasadas (negativos).

library(rgeoda)

Loading required package: digest

Attaching package: 'rgeoda'

The following objects are masked from 'package:sfdep':

    local_g, local_gstar, local_moran

The following object is masked from 'package:spdep':

    skater

covid_subset_posi <- covid %>%
  filter(FECHA_RESULTADO == "2020-12-11") %>%
  mutate(positividad = ifelse(METODODX == "PCR", 1, 0))

covid_scan_ppp <- ppp(covid_subset_posi$lon, 
                      covid_subset_posi$lat,
                      range(covid_subset_posi$lon),
                      range(covid_subset_posi$lat),
                      marks = as.factor(covid_subset_posi$positividad))

Aplicaremos la prueba de escaneo espacial propuesto por M. Kulldorff en SatScan e implementada en R en el paquete smacpod.

Por motivos de costo computacional utilizaremos 10 simulaciones (nsim) de Monte Carlo para determinar el valor-p de la prueba de hipótesis. Para otros propósitos, se recomienda incrementar el número de simulaciones.

covid_scan_test <- spscan.test(covid_scan_ppp,
                               nsim = 10, case = 2, 
                               maxd=.15, alpha = 0.05)

El objeto de tipo spscan contiene información del clúster detectado:

• locids: las localizaciones incluidas en el clúster
• coords: las coordenadas del centroide del clúster
• r: el radio del clúster
• rr: el riesgo relativo (RR) dentro del clúster
• pvalue: valor-p de la prueba de hipótesis calculado por simulaciones de Monte Carlo

entre otros.

covid_scan_test

method: circular scan
distance upperbound:  0.15
realizations: 10

Para representar gráficamente el clúster detectado, el subconjunto de análisis es convertido a una clase adecuada para la representación espacial.

# Construimos el centroide del clúster
cent <- tibble(lon = covid_scan_test$clusters[[1]]$coords[,1],
               lat = covid_scan_test$clusters[[1]]$coords[,2]) %>%
  st_as_sf(coords = c("lon", "lat"),crs = 4326)

# Construimos el área del clúster en base al radio
clust <- cent %>%
  st_buffer(dist = covid_scan_test$clusters[[1]]$r*111110)

Graficaremos el clúster detectado empleando el paquete mapview:

cluster <- mapview(clust, alpha.regions = 0, color = "red")

points <- covid_subset_posi %>%
  st_as_sf(coords = c("lon", "lat"), crs = 4326) %>%
  mapview(zcol = "positividad", alpha.regions = .4, alpha = 0)

points + cluster

25.8.2 Agrupamiento espacial basado en densidad de aplicaciones con ruido (DBSCAN)

Funciona agrupando las regiones de alta densidad y separándolas de las regiones de baja densidad. Su algoritmo más conocido es el (DBSCAN).

• EPS: distancia mínima para considerarse vecinos.
• MinPts: mínimo número de vecinos
• Uso: Mapear el efecto de un nuevo brote o trazar la ubicación de las estaciones meteorológicas de una ciudad.

En esta sección, emplearemos la metodología DBSCAN para la creación de clusters. Para ello, usaremos la base de datos ccpp-10km.csv, la cual contiene información sobre casos de malaria, dengue, leptospirosis y algunas variables ambientales y sociodemográficas correspondientes a 60 centros poblados ubicados a lo largo de la carretera Iquitos - Nauta, Loreto, Perú.

cp <- read_csv("data/ccpp-10km.csv")

Recordemos que trabajaremos con datos espaciales, por lo tanto, es importante convertir el objeto cp a un objeto espacial.

cp_sf <- cp %>%
  st_as_sf(coords = c("lng","lat"),crs = 4326)

cp_sf

Simple feature collection with 60 features and 21 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: -73.60862 ymin: -4.542548 xmax: -73.31898 ymax: -3.822999
Geodetic CRS:  WGS 84
# A tibble: 60 × 22
   ubigeo nomcp        dep   prov  dist  ubigeocp group poblacion dengue malaria
 *  <dbl> <chr>        <chr> <chr> <chr>    <dbl> <chr>     <dbl>  <dbl>   <dbl>
 1 160113 PENA NEGRA   LORE… MAYN… SAN …   1.60e9 INNO…       736 0.0217 0.00543
 2 160113 PUERTO ALME… LORE… MAYN… SAN …   1.60e9 INNO…       201 0      0.139  
 3 160113 UNION PROGR… LORE… MAYN… SAN …   1.60e9 INNO…       216 0      0.00463
 4 160113 NINA RUMI    LORE… MAYN… SAN …   1.60e9 INNO…       672 0      0.109  
 5 160113 NUEVA ESPER… LORE… MAYN… SAN …   1.60e9 INNO…        36 0      0.0278 
 6 160113 MORALILLO    LORE… MAYN… SAN …   1.60e9 INNO…       201 0      0.0398 
 7 160113 BUENA ESPER… LORE… MAYN… SAN …   1.60e9 INNO…        17 0      0      
 8 160113 SANTA BARBA… LORE… MAYN… SAN …   1.60e9 INNO…        40 0      0.025  
 9 160113 SAN CARLOS   LORE… MAYN… SAN …   1.60e9 INNO…        86 0      0      
10 160113 EL DORADO    LORE… MAYN… SAN …   1.60e9 INNO…        90 0      0.0111 
# ℹ 50 more rows
# ℹ 12 more variables: leptospirosis <dbl>, pr_avg <dbl>, ro_avg <dbl>,
#   soil_avg <dbl>, tmmx_avg <dbl>, tmmn_avg <dbl>, etp_avg <dbl>,
#   humidity_avg <dbl>, def_avg <dbl>, ghsl_avg <dbl>, ln_avg <dbl>,
#   geometry <POINT [°]>

Ahora visualizaremos la distribución de centros poblados en el espacio, pero coloreándolos en función de la incidencia de malaria,

mapview(cp_sf, zcol = "malaria", layer.name = "Incidencia de malaria")

Una vez que se han cargado nuestros datos al environment, será necesario realizar la proyección cartográfica para trabajar sobre unidades métricas.

cp_sf_utm <- cp_sf %>% 
  st_transform(32718)

cp_sf_utm

Simple feature collection with 60 features and 21 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: 654357.7 ymin: 9497753 xmax: 686656.3 ymax: 9577256
Projected CRS: WGS 84 / UTM zone 18S
# A tibble: 60 × 22
   ubigeo nomcp        dep   prov  dist  ubigeocp group poblacion dengue malaria
 *  <dbl> <chr>        <chr> <chr> <chr>    <dbl> <chr>     <dbl>  <dbl>   <dbl>
 1 160113 PENA NEGRA   LORE… MAYN… SAN …   1.60e9 INNO…       736 0.0217 0.00543
 2 160113 PUERTO ALME… LORE… MAYN… SAN …   1.60e9 INNO…       201 0      0.139  
 3 160113 UNION PROGR… LORE… MAYN… SAN …   1.60e9 INNO…       216 0      0.00463
 4 160113 NINA RUMI    LORE… MAYN… SAN …   1.60e9 INNO…       672 0      0.109  
 5 160113 NUEVA ESPER… LORE… MAYN… SAN …   1.60e9 INNO…        36 0      0.0278 
 6 160113 MORALILLO    LORE… MAYN… SAN …   1.60e9 INNO…       201 0      0.0398 
 7 160113 BUENA ESPER… LORE… MAYN… SAN …   1.60e9 INNO…        17 0      0      
 8 160113 SANTA BARBA… LORE… MAYN… SAN …   1.60e9 INNO…        40 0      0.025  
 9 160113 SAN CARLOS   LORE… MAYN… SAN …   1.60e9 INNO…        86 0      0      
10 160113 EL DORADO    LORE… MAYN… SAN …   1.60e9 INNO…        90 0      0.0111 
# ℹ 50 more rows
# ℹ 12 more variables: leptospirosis <dbl>, pr_avg <dbl>, ro_avg <dbl>,
#   soil_avg <dbl>, tmmx_avg <dbl>, tmmn_avg <dbl>, etp_avg <dbl>,
#   humidity_avg <dbl>, def_avg <dbl>, ghsl_avg <dbl>, ln_avg <dbl>,
#   geometry <POINT [m]>

En este paso, se extraerán las coordenadas de los centros poblados con el objetivo de calcular posteriormente las distancias entre cada uno de estos puntos.

coords <- st_coordinates(cp_sf_utm)

head(coords, n = 5)

            X       Y
[1,] 684683.3 9572819
[2,] 680109.1 9576303
[3,] 684469.1 9573520
[4,] 679233.1 9574863
[5,] 676138.2 9568067

A continuación, se procederá a calcular las distancias entre los centros poblados y sus vecinos más cercanos. Para ello utilizaremos la función KNNdist del paquete dbscan.

neighbor_dist <- kNNdist(coords, k = 4)

neighbor_dist

 [1]  2829.908  4519.982  2969.048  3871.127  5591.642  3410.429  3924.928
 [8]  3749.028  3793.399  4913.686  3943.174  3749.028  3756.907  3415.046
[15]  4023.387  4179.682  5391.226  6145.627  3925.873  3345.656  4835.194
[22]  4082.764  5677.497  3774.615  5322.620  3577.404  4083.963  3716.882
[29]  3607.233  3733.194  2608.921  9048.243  3265.646  5724.873  4960.441
[36]  4050.707  3577.404  4083.963  8239.099 12043.791  3927.281  3792.038
[43]  5030.040  2969.048  2490.458  3293.295 21432.585 13651.588 12782.073
[50] 12782.073 16087.023  4064.697  3498.121  3680.286  3265.646  5362.926
[57]  3443.652  3110.797  3257.366  3989.725

En este caso, el argumento k hace referencia al número de vecinos más cercanos usados para el cálculo de las distancias.

kNNdistplot <- function(neighbor_dist, k = 4) {
  sorted_dists <- sort(neighbor_dist)
  plot(1:length(sorted_dists), sorted_dists, type = 'b', pch = 19, 
       xlab = "Puntos ordenados", ylab = paste(k, "-NN Distance", sep = ""))
  abline(h = mean(sorted_dists), col = "red", lty = 2)
  abline(h = median(sorted_dists), col = "blue", lty = 2)
}

kNNdistplot(neighbor_dist, k = 4)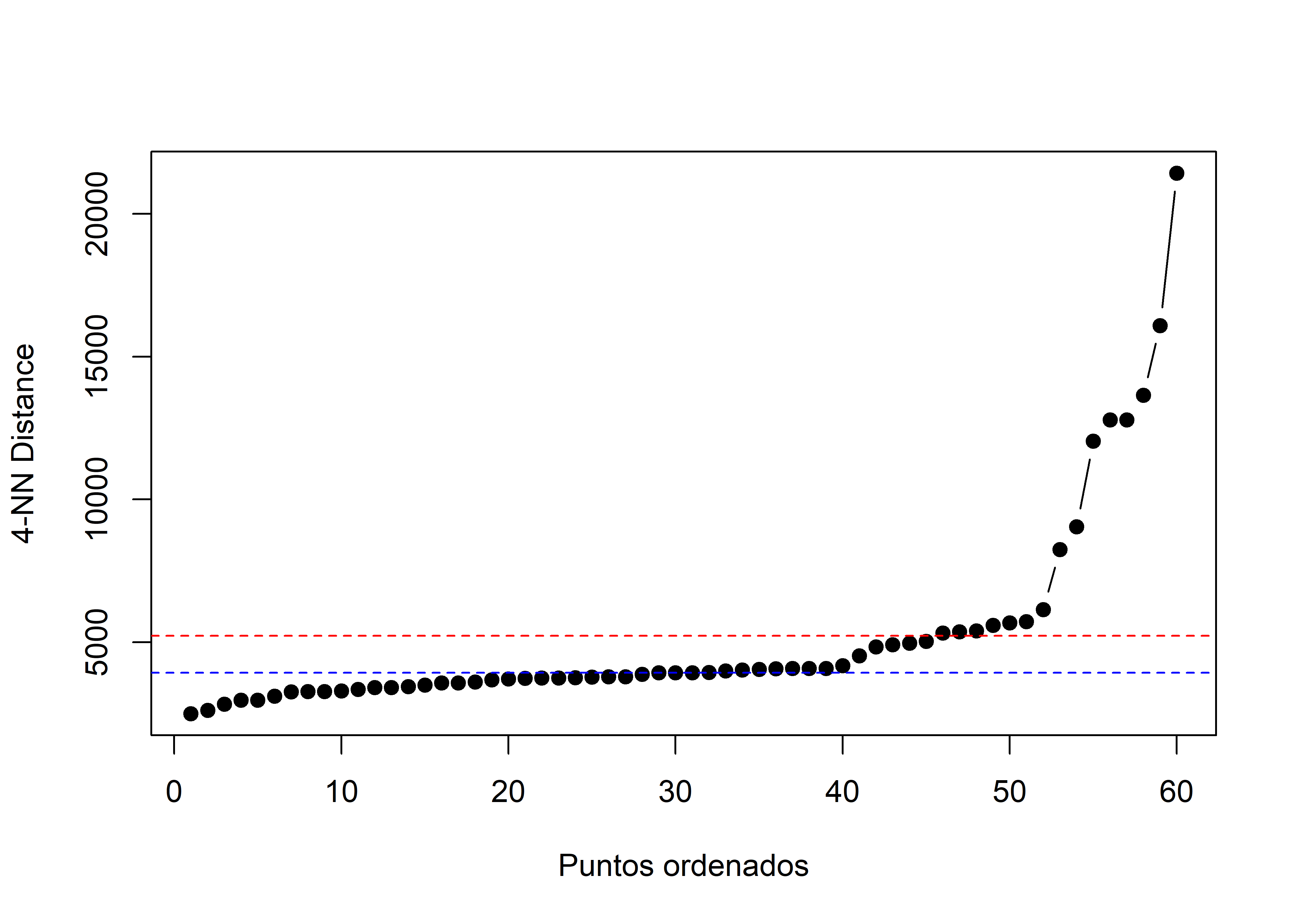

Del gráfico anterior, se puede concluir que el punto de quiebre en la curva ocurre en la posición 40.

neighbor_dist %>% 
  sort() %>% 
  nth(40)

[1] 4179.682

Entonces, este valor puede ser considerado como la distancia óptima para hacer el clustering,

optimal_eps <- 4179.682

Ahora, se realizará el cálculo del clustering. En este caso, el argumento minPts será configurado a 5, debido a que, hace referencia al número mínimo de puntos en la distancia requerida para el clustering, incluyendo el punto central. En el ejercicio anterior, se definieron 4 puntos como vecinos más cercanos.

c_dbscan <- dbscan(coords, eps = optimal_eps, minPts = 5)

Ahora, añadiremos los resultados de los clusters a los datos espaciales,

cp_dbscan <- cp_sf_utm %>% 
  mutate(dbscan_cluster = as.factor(c_dbscan$cluster))

Finalmente, visualizaremos los clusters utilizando ggplot,

cp_dbscan %>% 
  ggplot(aes(color = dbscan_cluster)) +
  geom_sf() +
  scale_color_viridis_d(option = "turbo") +
  theme_minimal() +
  labs(title = "Clusters - DBSCAN",
       color = "Clusters")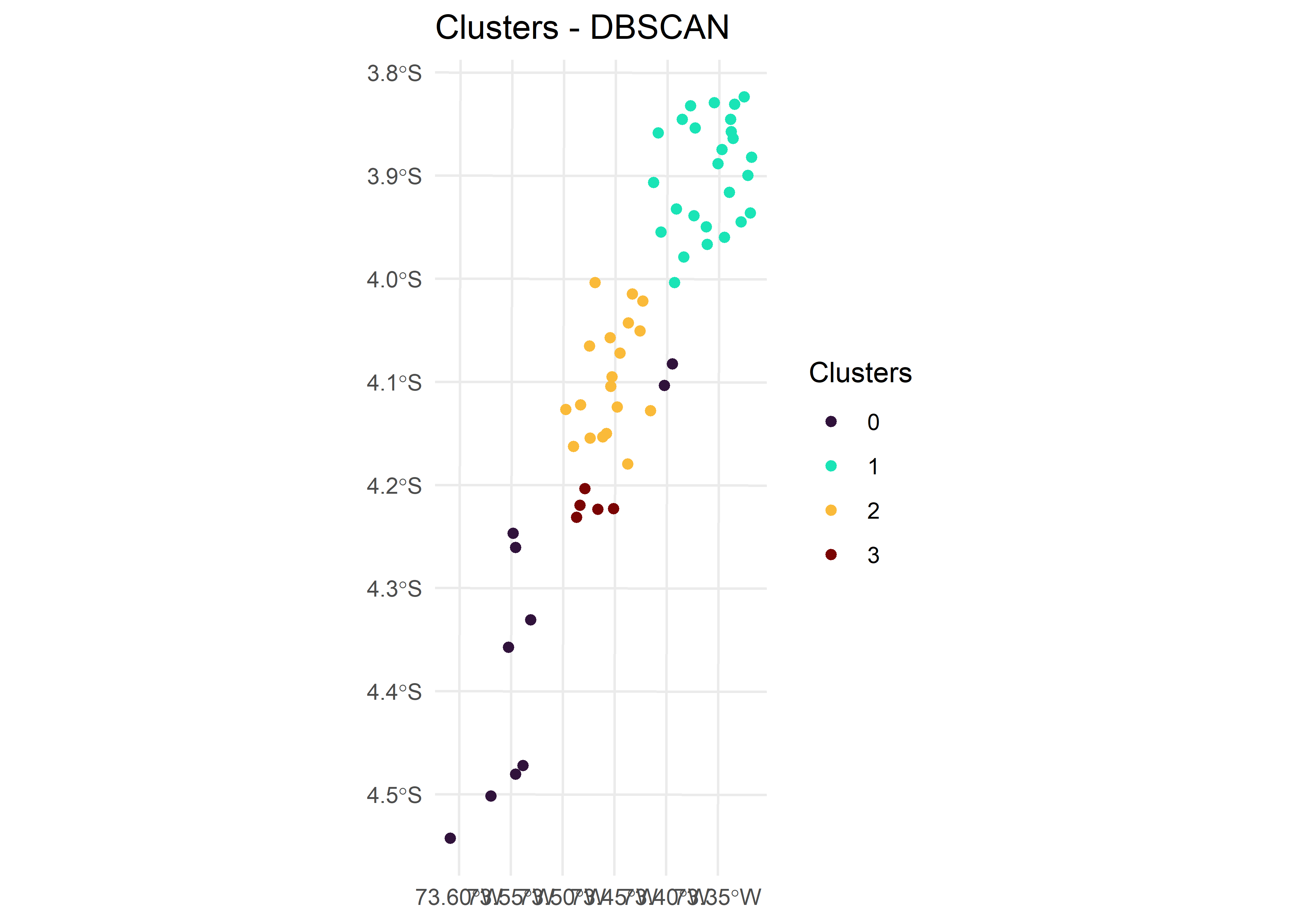

25.8.3 Análisis de “K”luster espacial por medio de eliminación de bordes del árbol (SKATER)

El algoritmo SKATER

El análisis espacial C(K)luster por eliminación de bordes de árboles (algoritmo SKATER) introducido por Assunção et al. (2006) se basa en la poda óptima de un árbol de mínima expansión que refleja la estructura de contigüidad entre las observaciones. Proporciona un algoritmo optimizado para podar el árbol en varios clústeres donde los valores de las variables seleccionadas sean lo más similares posible.

Para este ejercicio, consideraremos una matriz de vecindad de tipo reina y seguiremos utilizando el objeto cp_sf_utm.

queen_w <- queen_weights(cp_sf_utm)

Ahora, se generarán los clusters usando el algoritmo SKATER con la función skater del paquete `rgeoda. Primero, seleccionaremos todas las variables de interés y las almacenaremos en el objeto clust_vars.

clust_vars <- cp_sf_utm %>% 
  select(poblacion:ghsl_avg)

Luego de seleccionar nuestras variables de interés, correremos el algoritmo para la creación de clusters. El primer argumento de la función skater será el número de clusters, el segundo la matriz de vecindad y el tercero la base de datos.

c_skater <- skater(4, queen_w, clust_vars)

Ahora, añadiremos los resultados a la base de datos espacial.

cp_skater <- cp_sf_utm %>% 
  mutate(skater_cluster = as.factor(c_skater$Clusters) )

Finalmente, visualizaremos los resultados,

cp_skater %>% 
ggplot() +
  geom_sf(aes(color = skater_cluster)) +
  scale_color_viridis_d(option = "turbo") +
  theme_minimal() +
  labs(title = "Clusters - SKATER",
       color  = "Cluster")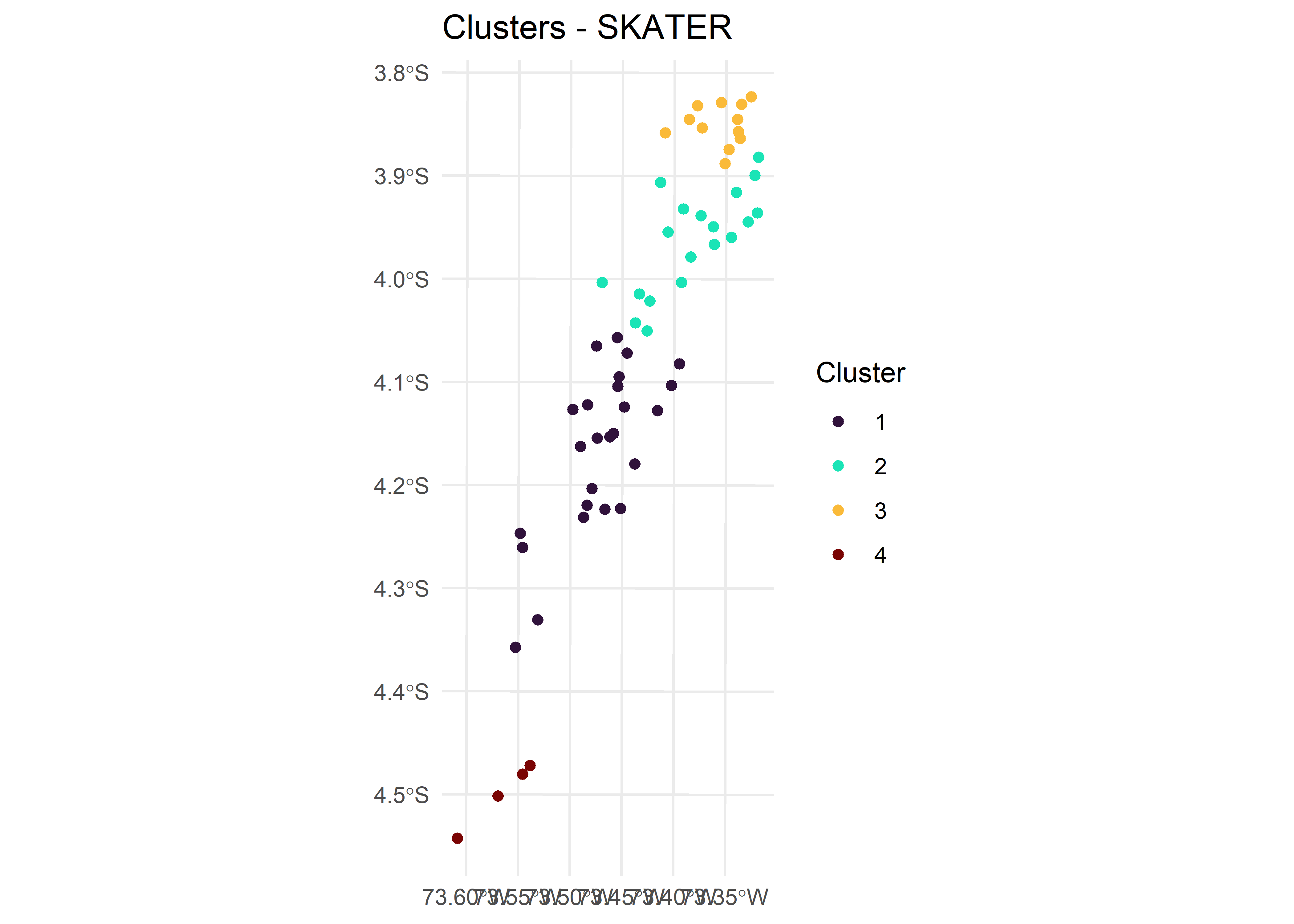

25.9 Modelos predictivos espaciales

Para este apartado usaremos algunos paquetes adicionales pertenecientes a tidymodels, además de los empleados al inicio de este capítulo:

library(tidymodels)
library(spatialsample)
library(randomForest)

Además, usaremmos los datos de un estudio sobre malaria en Oromia (Etiopía) en el 2009. Los datos se encuentran alojados en el repositorio de Malaria Atlas Project y podemos descargarlo también desde un repositorio en Github.

malaria_eth <- read_csv("data/mal_data_eth_2009_no_dups.csv")

Rows: 203 Columns: 17
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (8): country, country_id, continent_id, site_name, rural_urban, method, ...
dbl (9): site_id, latitude, longitude, year_start, lower_age, upper_age, exa...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

malaria_eth

# A tibble: 203 × 17
   country  country_id continent_id site_id site_name         latitude longitude
   <chr>    <chr>      <chr>          <dbl> <chr>                <dbl>     <dbl>
 1 Ethiopia ETH        Africa          6694 Dole School           5.90      38.9
 2 Ethiopia ETH        Africa          8017 Gongoma School        6.32      39.8
 3 Ethiopia ETH        Africa         12873 Buriya School         7.57      40.8
 4 Ethiopia ETH        Africa          6533 Arero School          4.72      38.8
 5 Ethiopia ETH        Africa          4150 Gandile School        4.89      37.4
 6 Ethiopia ETH        Africa          1369 Melka Amana Scho…     6.25      39.8
 7 Ethiopia ETH        Africa          5808 Ebisa School          7.17      40.6
 8 Ethiopia ETH        Africa          8922 Dhedecha Ferde S…     6.75      41.2
 9 Ethiopia ETH        Africa         19345 Kuni Oulaoulo Sc…     5.95      39.3
10 Ethiopia ETH        Africa           634 Halo Choma School     6.84      41.1
# ℹ 193 more rows
# ℹ 10 more variables: rural_urban <chr>, year_start <dbl>, lower_age <dbl>,
#   upper_age <dbl>, examined <dbl>, pf_pos <dbl>, pf_pr <dbl>, method <chr>,
#   title1 <chr>, citation1 <chr>

Usaremos la información de las coordenadas para crear un objeto sf que contenga la información de las geometrías (puntos). Además, la variable pf_pos estará dicotimizada en 1 (positivo) y 0 (negativo).

cases <- malaria_eth %>%
  st_as_sf(coords = c("longitude", "latitude"), 
           crs = 4326, remove = FALSE) %>%
  mutate(pf_pos = ifelse(pf_pos > 0, 1, 0),
         pf_pos = factor(pf_pos)) %>%
  select(pf_pos, longitude, latitude)
cases

Simple feature collection with 203 features and 3 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: 34.5418 ymin: 3.8966 xmax: 42.4915 ymax: 9.9551
Geodetic CRS:  WGS 84
# A tibble: 203 × 4
   pf_pos longitude latitude         geometry
   <fct>      <dbl>    <dbl>      <POINT [°]>
 1 0           38.9     5.90 (38.9412 5.9014)
 2 0           39.8     6.32 (39.8362 6.3175)
 3 0           40.8     7.57 (40.7521 7.5674)
 4 0           38.8     4.72  (38.765 4.7192)
 5 0           37.4     4.89  (37.3632 4.893)
 6 1           39.8     6.25 (39.7891 6.2461)
 7 0           40.6     7.17  (40.649 7.1657)
 8 0           41.2     6.75 (41.1559 6.7542)
 9 1           39.3     5.95 (39.2547 5.9471)
10 0           41.1     6.84 (41.0551 6.8386)
# ℹ 193 more rows

Para visualizar estos datos en un mapa, seleccionaremos la región de Oromia de Etiopía y usaremos la librería ggplot2 para crear la visualización:

Oromia <- gadm(country = "ETH", level = 1, path= ".", resolution = 2) %>%
  st_as_sf() %>%
  filter(NAME_1=="Oromia")

ggplot() + 
  geom_sf(data = Oromia, fill = NA) + 
  geom_sf(data = cases, aes(col = pf_pos)) +
  scale_color_manual(values = c("gray", "red")) + 
  theme_bw()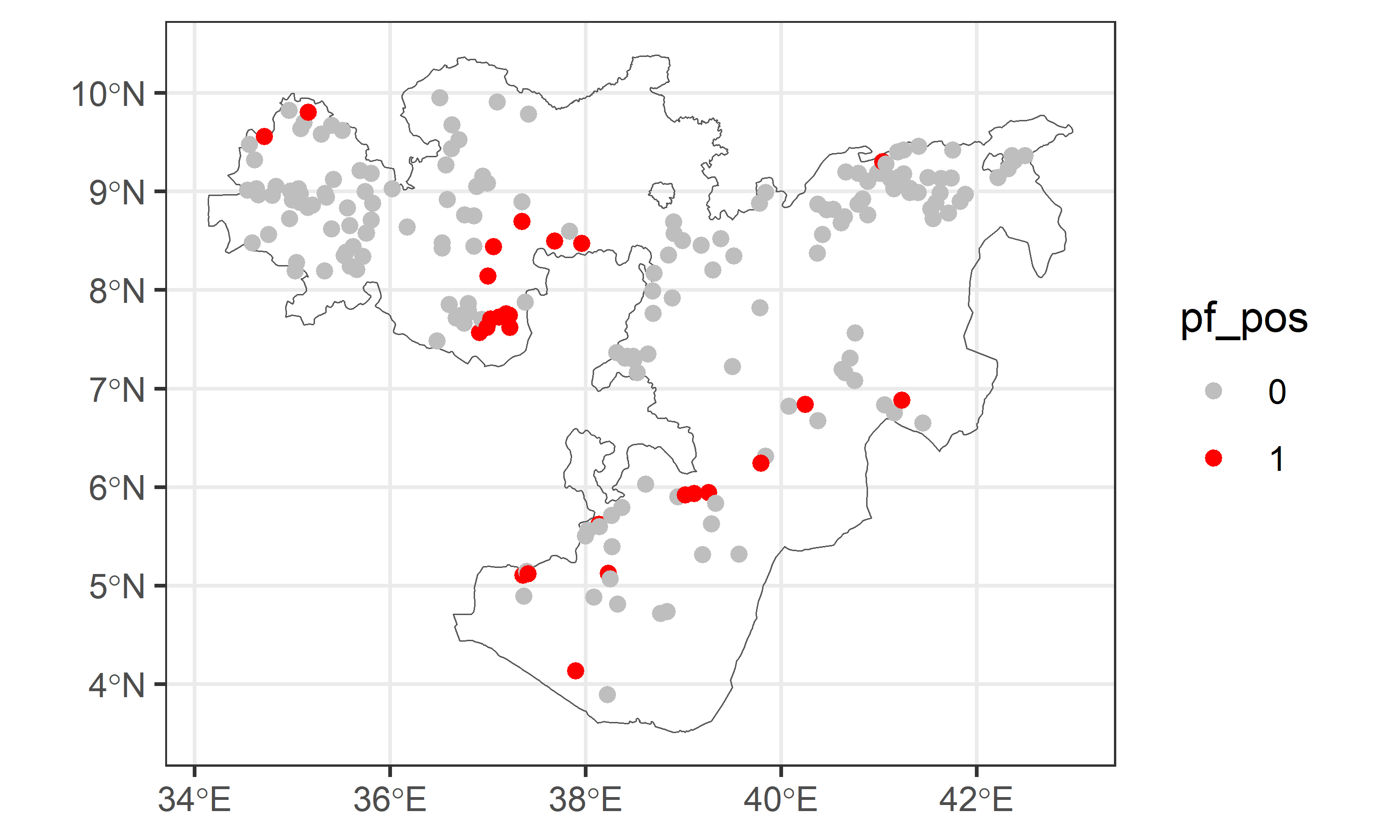

Utilizaremos los datos bioclimáticos para realizar un análisis predictivo. Estos datos se descargarán y se ajustarán a la región de Oromia:

bioclim <- geodata::worldclim_country(country = "ETH", var = "bio",
                                res = 10, path = ".") %>%
  mask(Oromia)

Para entender mejor las variables bioclimáticas, realizaremos una visualización interactiva con el paquete mapview. Esto permite identificar patrones y variaciones en las condiciones climáticas en la región de interés.

mapview(bioclim, maxpixels = 49248000)

En vista de lo anterior, integraremos los datos de los casos de malaria con los datos bioclimáticos para poder elaborar algunos modelos predictivos:

malaria_climate_cases <- bind_cols(cases,
                                   extract(bioclim, cases)) %>%
  drop_na() 

25.9.1 Validación cruzada

A fin de tener una estimación más robusta y estable, emplearemos una técnica de validación cruzada que consiste en obtener varias particiones de los datos para evaluar el rendimiento del modelo de manera más exhaustiva. Específicamente, utilizaremos dos enfoques de validación cruzada:

1. Validación Cruzada Aleatoria: Este método divide aleatoriamente los datos en varios subconjuntos (folds). Sin embargo, solo lo hace en función de un proceso aleatorio simple en el que cada observación tiene el mismo nivel de importancia. Así, información como la ubicación geográfica, no es tomada en consideración.

bad_folds <- malaria_climate_cases %>%
  vfold_cv(v = 5) 

2. Validación Cruzada con Agrupamiento Espacial: Dado que los datos de malaria y clima tienen una estructura espacial, este método agrupa los datos en función de su proximidad geográfica antes de realizar la partición en pliegues. Esto ayuda a evitar algún sesgo en el rendimiento del modelo al considerar las características espaciales de los datos.

good_folds <- malaria_climate_cases %>%
  spatial_clustering_cv(v = 5)

25.9.2 Configuración de los modelos

Para los modelos, configuramos 2 workflow que emplean 2 algoritmos diferentes de predicción: regresión logística y random forest (rf). La variable a explicar será la de pf_pos; y las predictoras, las de bioclima. Para poder emplearlas en los análisis, primero seleccionaremos las variables bioclimáticas y las almacenaremos en un vector:

predictors_malaria <- malaria_climate_cases %>%
  st_drop_geometry() %>%
  dplyr::select(starts_with("wc")) %>%
  names() %>%
  paste(collapse = " + ")
predictors_malaria

[1] "wc2.1_30s_bio_1 + wc2.1_30s_bio_2 + wc2.1_30s_bio_3 + wc2.1_30s_bio_4 + wc2.1_30s_bio_5 + wc2.1_30s_bio_6 + wc2.1_30s_bio_7 + wc2.1_30s_bio_8 + wc2.1_30s_bio_9 + wc2.1_30s_bio_10 + wc2.1_30s_bio_11 + wc2.1_30s_bio_12 + wc2.1_30s_bio_13 + wc2.1_30s_bio_14 + wc2.1_30s_bio_15 + wc2.1_30s_bio_16 + wc2.1_30s_bio_17 + wc2.1_30s_bio_18 + wc2.1_30s_bio_19"

1. Regresión Logística: Este modelo se puede usar para la predicción de la probabilidad de un outcome binario (por ejemplo, presencia o ausencia de malaria) a partir de varias variables independientes (las variables climáticas):

lr_recipe <- workflow() %>%
  add_formula(as.formula(paste("pf_pos ~", predictors_malaria))) %>%
  add_model(logistic_reg(mode = "classification", engine = "glm"))

2. Random Forest: Este modelo de aprendizaje automático utiliza múltiples árboles de decisión para mejorar la precisión y robustez de las predicciones:

rf_recipe <- workflow() %>%
  add_formula(as.formula(paste("pf_pos ~", predictors_malaria))) %>%
  add_model(boost_tree(mode = "classification", engine = "xgboost"))

25.9.3 Ejecución y evaluación del modelo

Para medir el desempeño de los modelos, se utilizan varias métricas, como el AUC del ROC, la precisión, el recall y la exactitud. Estas métricas proporcionan una visión integral de cómo los modelos predicen la incidencia de malaria. Para hacer esto, configuramos estas métricas de la siguiente manera:

metrics <- metric_set(roc_auc, accuracy, recall, precision)
metrics

A metric set, consisting of:
- `roc_auc()`, a probability metric | direction: maximize
- `accuracy()`, a class metric      | direction: maximize
- `recall()`, a class metric        | direction: maximize
- `precision()`, a class metric     | direction: maximize

Ahora, podemos evaluar las métricas de los modelos en los folds de validación cruzada creadas previamente y evaluarlas para seleccionar el modelo más adecuado:

1. Regresión Logística con Validación Aleatoria:

regular_lr <- fit_resamples(lr_recipe, bad_folds, metrics = metrics)
collect_metrics(regular_lr)

# A tibble: 4 × 6
  .metric   .estimator  mean     n std_err .config             
  <chr>     <chr>      <dbl> <int>   <dbl> <chr>               
1 accuracy  binary     0.816     5  0.0175 Preprocessor1_Model1
2 precision binary     0.887     5  0.0276 Preprocessor1_Model1
3 recall    binary     0.911     5  0.0360 Preprocessor1_Model1
4 roc_auc   binary     0.728     5  0.0465 Preprocessor1_Model1

2. Regresión Logística con Validación Espacial:

spatial_lr <- fit_resamples(lr_recipe, good_folds, metrics = metrics)
collect_metrics(spatial_lr)

# A tibble: 4 × 6
  .metric   .estimator  mean     n std_err .config             
  <chr>     <chr>      <dbl> <int>   <dbl> <chr>               
1 accuracy  binary     0.617     5  0.109  Preprocessor1_Model1
2 precision binary     0.815     5  0.0858 Preprocessor1_Model1
3 recall    binary     0.695     5  0.132  Preprocessor1_Model1
4 roc_auc   binary     0.333     5  0.0421 Preprocessor1_Model1

25.9.3.1 Random Forest con Validación Espacial:

spatial_rf <- fit_resamples(rf_recipe, good_folds, metrics = metrics)
collect_metrics(spatial_rf)

# A tibble: 4 × 6
  .metric   .estimator  mean     n std_err .config             
  <chr>     <chr>      <dbl> <int>   <dbl> <chr>               
1 accuracy  binary     0.745     5  0.0911 Preprocessor1_Model1
2 precision binary     0.851     5  0.0644 Preprocessor1_Model1
3 recall    binary     0.875     5  0.0990 Preprocessor1_Model1
4 roc_auc   binary     0.313     5  0.106  Preprocessor1_Model1

25.9.4 Modelos finales

Finalmente, se muestra los modelos tanto del modelo logístico como de random forest y el uso de sus predicciones mediante la visualización de las mismas.

25.9.4.1 Regresión logística:

fit_lr <- malaria_climate_cases %>%
  st_drop_geometry() %>% 
  dplyr::select(pf_pos, starts_with("wc")) %>%  
  glm(pf_pos ~ .,
      family = binomial(),
      data = .)

Mediante la función predict podemos calcular el resultado del modelo y asignarlo a los datos de origen (bioclim).

pred_lr <- predict(model = fit_lr, 
                   object = bioclim, 
                   typ = "response")
mapview(pred_lr)

25.9.4.2 Random forest:

fit_rf <- malaria_climate_cases %>%
  st_drop_geometry() %>% 
  dplyr::select(-c(longitude, latitude, ID)) %>%  
  randomForest(pf_pos ~ ., 
               data = .)

pred_rf <- 1 - predict(model = fit_rf, 
                       object = bioclim, 
                       type = "prob")
mapview(pred_rf)