20 Estudios de cohorte
20.1 Paquetes y data
En este capítulo utilizaremos un subconjunto de datos del estudio de Framingham, el cual se encuentra alojado en el objeto framingham. Es importante mencionar que dicha base de datos ha sido modificada por los autores con fines académicos.
framingham <- read_csv("data/framingham_cohort_dataset.csv")A continuación se proporciona una breve descripción sus variables.
| Descripción | Variable |
|---|---|
| Código individual del participante | RANDID |
| Fecha de enrolamiento | START_DATE |
| Periodo del estudio | PERIOD |
| Fecha de la visita | VISIT_DATE |
| Hipertensión al basal, 1 = Hipertenso Prevalente, 0 = No Hipertenso | PREVHYP |
| Hipertensión durante el seguimiento, 1 = Hipertenso, 0 = No Hipertenso | HYPERTEN |
| Fecha del evento o censura | EVENT_CENSOR_DATE |
| Sexo, 1 = Masculino, 2 = Femenino | SEX |
| Edad en años al momento de la evaluación | AGE |
| Número de cigarrilos fumados por día | CIGPDAY |
| Índice de masa corporal | BMI |
| Antecedente de diabetes, 1 = Diabético, 0 = No Diabético | DIABETES |
20.2 Diseño de estudio
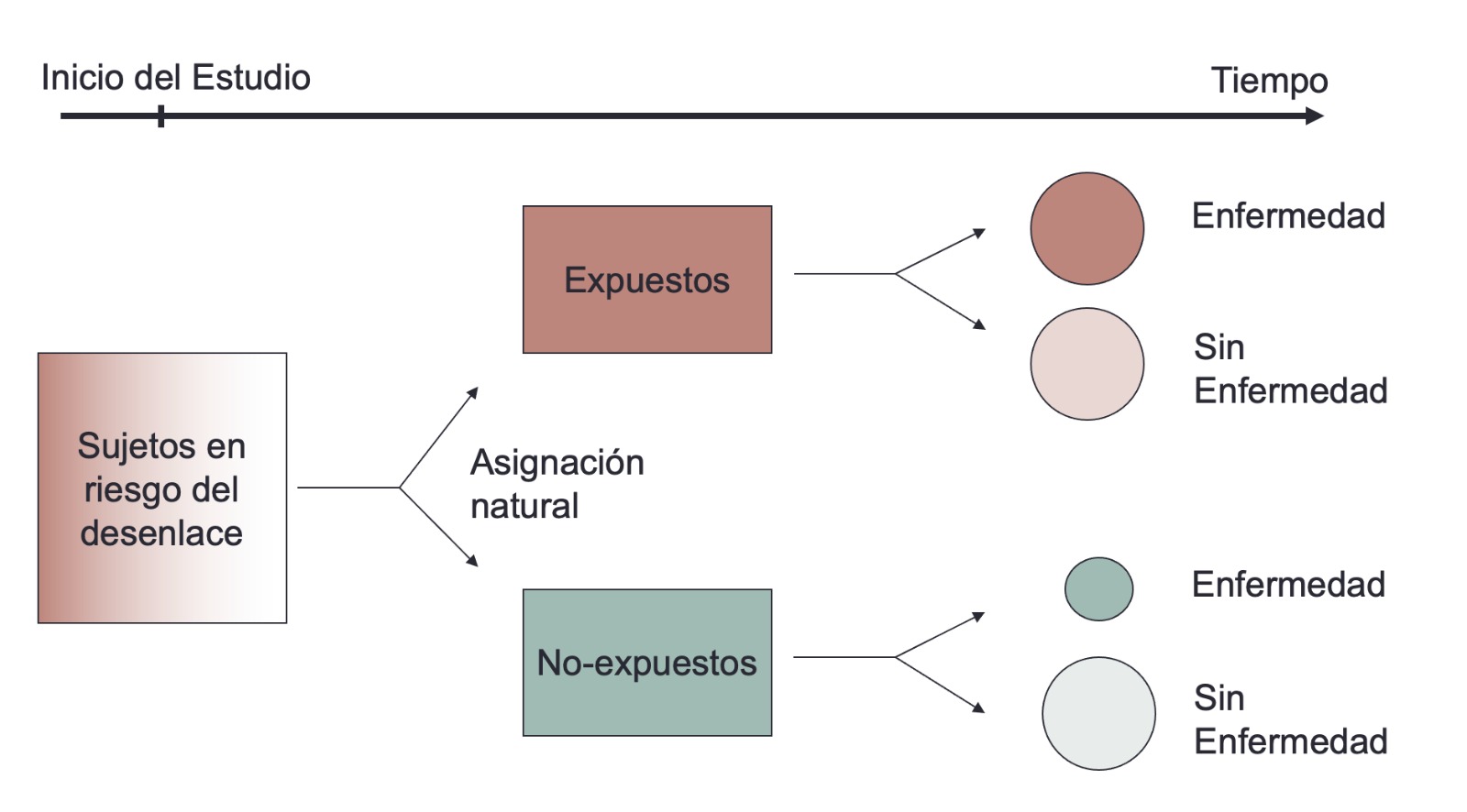
En este tipo de estudio observacional se selecciona a un grupo de individuos, estos son asignados naturalmente al grupo de expuestos y no expuestos a un factor de interés. Luego se realiza el seguimiento para comparar la incidencia de la enfermedad en ambos grupos. El diseño puede incluir más de dos grupos de comparación (no expuestos, expuestos a baja dosis, expuestos a alta dosis , etc.).
En este tipo de estudio se puede determinar una relación temporal entre la exposición y la enfermedad debido a que se estan identificando casos nuevos (incidentes).
20.3 Esquema básico:
- Se selecciona un grupo de sujetos para el seguimiento (cohorte).
- Se clasifican a los sujetos de estudio en expuestos y no expuestos a uno o varios factores de interés
- Se determina la incidencia de la enfermedad en el grupo expuesto y no expuesto y se comparan los riesgos de la enfermedad entre ellos.
- La razón del riesgo de enfermedad se interpreta como asociación positiva (riesgo) o negativa (protección) entre la exposición y la enfermedad.
20.4 Tipos de cohortes
20.4.1 Cohorte cerrada
Es aquella que tiene una cantidad fija de participantes. Una vez se tenga definida la cohorte y se haya dado inicio al seguimiento, ningún participante adicional puede ser añadido. Sin embargo, el número inicial de participantes incluidos en la cohorte puede verse reducido a medida que se presente el evento, los participantes se pierdan durante el seguimiento o mueran. En el mejor de los casos, los investigadores en este tipo de cohortes intentan localizar a los participantes si ellos han dejado la zona de estudio. Es así que, los participantes de una cohorte cerrada constituyen un grupo de personas que pueden pertenecer a la cohorte incluso aún si han abandonado el área de estudio.
20.4.2 Cohorte abierta
También conocida como cohorte dinámica o población dinámica, es aquella que puede recibir nuevos participantes a medida que pasa el tiempo. En este tipo de cohorte, la cual se encuentra definida geográficamente, los participantes dejan de pertenecer a la cohorte, y por ende dejan de ser seguidos, cuando abandonan los límites geográficos del área de estudio.
20.5 Tipos de estudios de cohortes
20.5.1 Estudios de cohorte prospectivo
También conocido como estudio longitudinal o estudio de cohortes concurrente. En este tipo de estudio, la población es identificada al inicio del estudio, y se siguen a todos los sujetos al mismo tiempo a lo largo del periodo de estudio hasta que se presente o no el evento de interés.
20.5.2 Estudios de cohorte retrospectivo
También conocido como estudio de cohortes prospectivo no concurrente o estudio de cohortes histórico. Este tipo de estudio mantiene el diseño de cohortes, es decir, aún estamos comparando un grupo expuesto versus un grupo no expuesto; sin embargo, la diferencia recae en que el estudio de cohorte retrospectivo utiliza datos del pasado (históricos) para poder reducir los tiempos y obtener resultados rápidos.
20.6 Selección de las poblaciones de estudio
Las estrategias para seleccionar a los grupos expuestos y no expuestos se pueden caracterizar de dos formas:
Se puede crear una población de estudio mediante la selección de grupos ya caracterizados como expuestos y no expuestos, por ejemplo, seleccionar a los trabajadores de una fábrica que están expuestos al mercurio y los que no están expuestos.
Se puede seleccionar una población definida antes de que cualquier de sus miembros se exponga a un factor de interés, luego mediante pruebas de laboratorio o cuestionarios de evaluación, se identifican los grupos expuestos y no expuestos. El ejemplo por excelencia es la cohorte de Framingham, donde se seleccionó a toda la población de un determinado lugar. En este caso, la exposición de interés puede no presentarse durante un largo tiempo, por lo tanto la duración del seguimiento será aún mayor que la primera estrategia.
Estamos interesados en evaluar la asociación entre la hipertensión arterial (HYPERTEN) y el número de cigarrillos consumidos por día (CIGPDAY), ajustando por sexo (SEX), edad (AGE), índice de masa corporal (BMI) y antecedente de diabetes (DIABETES).
Antes de ejecutar algún modelo de regresión, exploraremos rápidamente la base de datos.
glimpse(framingham)Rows: 11,627
Columns: 12
$ RANDID <dbl> 2448, 2448, 6238, 6238, 6238, 9428, 9428, 10552, 105…
$ START_DATE <date> 1956-01-26, 1956-01-26, 1956-05-08, 1956-05-08, 195…
$ PERIOD <dbl> 1, 3, 1, 2, 3, 1, 2, 1, 2, 1, 2, 3, 1, 2, 3, 1, 2, 1…
$ VISIT_DATE <date> 1962-01-24, 1974-01-21, 1962-05-07, 1968-05-05, 197…
$ PREVHYP <dbl> 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0…
$ HYPERTEN <dbl> 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ EVENT_CENSOR_DATE <date> 1980-01-26, 1980-01-26, 1980-05-08, 1980-05-08, 198…
$ SEX <dbl> 1, 1, 2, 2, 2, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2…
$ AGE <dbl> 39, 52, 46, 52, 58, 48, 54, 61, 67, 46, 51, 58, 43, …
$ CIGPDAY <dbl> 0, 0, 0, 0, 0, 20, 30, 30, 20, 23, 30, 30, 0, 0, 0, …
$ BMI <dbl> 26.97, NA, 28.73, 29.43, 28.50, 25.34, 25.34, 28.58,…
$ DIABETES <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0…Las variables Hipertensión al basal (PREVHYP), hipertensión durante el seguimiento (HYPERTEN), sexo (SEX) y antecedente de diabetes (DIABETES) tienen que ser factorizadas para poder continuar con nuestros análisis.
framingham_fct <- framingham %>%
mutate(SEX = case_when(SEX == 2 ~ 0,
TRUE ~ SEX),
SEX = factor(SEX,
levels = c(0, 1),
labels = c("Femenino", "Masculino")),
PREVHYP = factor(PREVHYP,
levels = c(0, 1),
labels = c("No hipertenso", "Hipertenso Prevalente")),
DIABETES = factor(DIABETES,
levels = c(0, 1),
labels = c("No Diabetico", "Diabetico"))
)Una vez que tengamos las variables convertidas a tipo factor, eliminaremos aquellos registros que tuvieron hipertensión al inicio del estudio, ya que, no formarán parte del análisis.
Adicionalmente, calcularemos los tiempos aportados por cada participante al estudio. Para ello, realizaremos la diferencia entre las columnas EVENT_CENSOR_DATE y START_DATE.
Ahora elaboraremos el gráfico de seguimiento de acuerdo a los periodos de los siguiente participantes de la cohorte de Framingham,
- Participantes ID: 2448, 6238, 43522, 123622, 33555
framingham_free_hyp %>%
filter(RANDID %in% c("2448", "6238", "43522", "123622", "33555")) %>%
mutate(RANDID = factor(RANDID),
HYPERTEN = factor(HYPERTEN,
levels = c(0, 1),
labels = c("No hipertenso", "Hipertenso"))) %>%
ggplot(aes(x = PERIOD, y = RANDID, group = RANDID, col = HYPERTEN)) +
geom_line(size = 1) +
geom_point(size = 4) +
scale_color_lancet() +
theme_bw() +
labs(x = "Periodos de Seguimiento",
y = "ID Participante",
title = "Seguimiento de pacientes del estudio de Framingham",
col = "Hipertensión")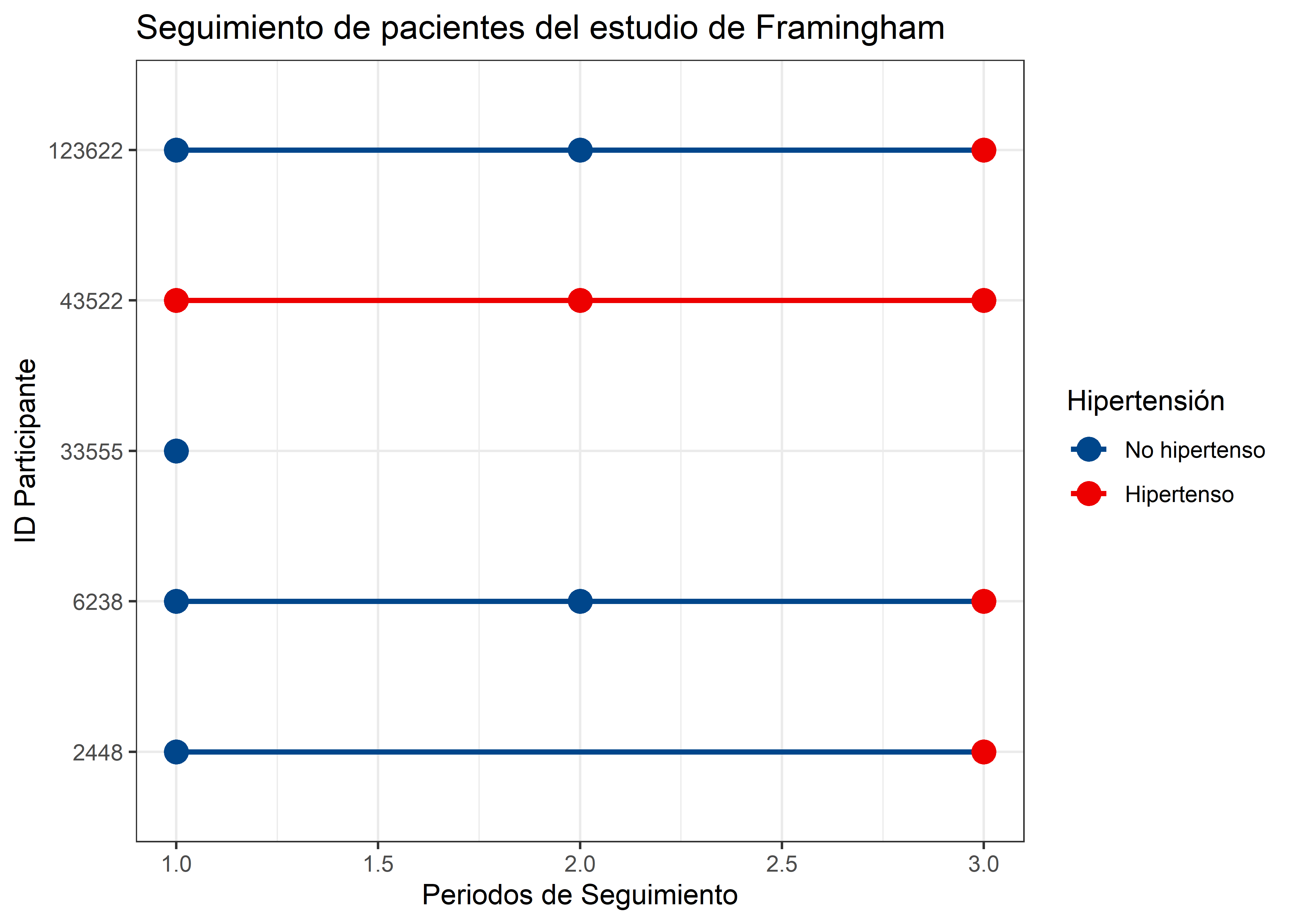
20.7 Regresión de Poisson
La regresión de Poisson es una técnica estadística utilizada para modelar datos de conteo, como el número de eventos que ocurren en un intervalo de tiempo o espacio dado. En el contexto de un estudio de cohortes, el riesgo relativo (RR) emerge como una medida de asociación fundamental y puede calcularse a partir de los coeficientes estimados en un modelo de regresión de Poisson.
Supongamos que tienes un modelo de regresión de Poisson simple con una variable predictora X de la siguiente manera:
Donde:
- n(λ) es el logaritmo de la tasa de incidencia (o el logaritmo del número de eventos esperados).
- β0 es el intercepto del modelo.
- β1, β2, …, βn son los coeficientes estimados para las variables predictoras X1, X2, …, Xn..
En el contexto de un modelo de regresión de Poisson, los coeficientes estimados se utilizan para calcular el logaritmo del riesgo relativo (RR). Recordemos del capítulo de Medidas de asociación, que el RR se calcula como la razón de incidencias entre el grupo con expuesto y sin exposición. Para obtener el RR, exponenciamos del coeficiente asociado a la variable de interés del modelo de poisson.
20.7.1 Modelo de regresión de Poisson sin offset
Debido a que el estudio de Framingham es una cohorte, debemos estimar las medidas correspondientes para este diseño. La primera medida que calcularemos será la razón de proporción de incidencias o razón de incidencias acumuladas. Para ello, utilizaremos la regresión de Poisson sin considerar el offset.
20.7.1.1 Tasas individuales: variable binaria y denominador.
El objeto hyper_cases contiene a cada sujeto del estudio de Framingham como una observación en la base de datos. Es por ello que, en estos casos, modelaremos la razón de incidencias acumuladas a nivel individual.
Sabemos que en un estudio de cohortes un individuo puede repetirse más de una vez en la base de datos debido a que se registran múltiples visitas/mediciones en el tiempo. Por tal motivo, para la estimación solo seleccionaremos al último registro de cada sujeto (RANDID) utilizando la función slice_tail() y configurando el argumento n=1.
El objeto hyper_cases contiene los registros/mediciones finales de cada individuo, por lo que ya podríamos utilizarlo para nuestros ejercicios.
Recordemos que nuestro objetivo es explorar la asociación entre la hipertensión arterial (HYPERTEN) y el número de cigarrillos consumidos por día (CIGPDAY), ajustando por sexo (SEX), edad (AGE), índice de masa corporal (BMI) y antecedente de diabetes (DIABETES). Es por ello que, con esa información podremos realizar el modelo de regresión de Poisson.
model_1 <- glm(HYPERTEN ~ CIGPDAY + AGE + BMI + SEX + DIABETES,
family = poisson(link="log"),
data = hyper_cases)
model_1_tidy <- tidy(model_1, conf.int = T, exponentiate = T) %>%
datatable(
options = list(
display = "compact",
pageLength = 10,
scrollX = TRUE
)
)
model_1_tidyInterpretación del coeficiente de CIGPDAY: En la población de estudio, la incidencia acumulada de hipertensión arterial es 0.996 (IC95%: 0.992 - 1.000) cuando el consumo de cigarrillos por día incrementa en una unidad, ajustando por edad, índice de masa corporal, sexo y condición de diabetes. Sin embargo, este resultado no es estadísticamente significativo (p=0.082).
20.7.1.2 Tasas agrupadas: variable de conteo y denominador
El objeto hyper_cases puede servir también para modelar tasas agrupadas si es que manipulamos los datos. Para este caso, agruparemos la base por Periodo (PERIOD), condición de diabetes (DIABETES) y sexo (SEX), y obtendremos el número de casos de hipertensión (HYPERTEN), la media de edad (EDAD), índice de masa corporal (BMI) y cigarrillos consumidos al día (CIGPDAY).
model_2 <- glm(hyperten_cases ~ CIGPDAY + AGE + BMI + SEX + DIABETES,
family = poisson(link="log"),
data = hyper_cases_grouped)
model_2_tidy <- tidy(model_2, conf.int = T, exponentiate = T) %>%
datatable(
options = list(
display = "compact",
pageLength = 10,
scrollX = TRUE
)
)
model_2_tidy`
Interpretación del coeficiente de CIGPDAY: En la población de estudio, la incidencia acumulada de hipertensión arterial es 0.941 (IC95%: 0.893 - 0.992) cuando el consumo de cigarrillos por día incrementa en una unidad, ajustando por edad, índice de masa corporal, sexo y condición de diabetes. Siendo este resultado estadísticamente significativo (p=0.023).
20.7.2 Modelo de regresión de Poisson con offset
En el contexto de análisis de datos de conteo, a menudo encontramos una variable de exposición que cuantifica la cantidad de veces que el evento de interés podría haber ocurrido. Para incorporar efectivamente esta variable en un modelo de regresión de Poisson, se utiliza lo que se conoce como unoffset.
Donde:
- λ es la tasa de incidencia o densidad de incidencia.
- β0, β1, β2, …, βn son los coeficientes estimados para las covariables.
- X1, X2, …, Xn son los valores de las covariables.
- ln(O) es el término de offset, que representa el logaritmo natural de la variable de exposición.
20.7.2.1 Tasas individuales: variable binaria y denominador.
A continuación, calcularemos la razón de tasas de incidencia a partir de los dos objetos previamente calculados. Para llevar a cabo este cálculo, emplearemos un modelo de regresión de Poisson en el que configuraremos adecuadamente el término de offset.
model_3 <- glm(HYPERTEN ~ CIGPDAY + AGE + BMI + SEX + DIABETES,
family = poisson(link="log"),
offset = log(time_follow_up),
data = hyper_cases)
model_3_tidy <- tidy(model_3, conf.int = T, exponentiate = T) %>%
datatable(
options = list(
display = "compact",
pageLength = 10,
scrollX = TRUE
)
)
model_3_tidyInterpretación del coeficiente de CIGPDAY: En la población de estudio, la tasa de incidencia de hipertensión arterial es 0.994 (IC95%: 0.990 - 0.998) cuando el consumo de cigarrillos por día incrementa en una unidad, ajustando por sexo, edad, índice de masa corporal y condición de diabetes. Siendo este resultado estadísticamente significativo (p=0.006).
20.7.2.2 Tasas agrupadas: variable de conteo y denominador
Para el cálculo de la tasas de incidencias agrupadas utilizaremos el objeto hyper_cases_grouped con el offest de la variable total.
model_4 <- glm(hyperten_cases ~ CIGPDAY + AGE + BMI + SEX + DIABETES,
family = poisson(link="log"),
offset = log(total),
data = hyper_cases_grouped)
model_4_tidy <- tidy(model_4, conf.int = T, exponentiate = T) %>%
datatable(
options = list(
display = "compact",
pageLength = 10,
scrollX = TRUE
)
)
model_4_tidyInterpretación del coeficiente de CIGPDAY: En la población de estudio, la tasa de incidencia de hipertensión arterial es 1.048 (IC95%: 0.990 - 1.109) cuando el consumo de cigarrillos por día incrementa en una unidad, ajustando por sexo, edad, índice de masa corporal y condición de diabetes. Sin embargo, este resultado no es estadísticamente significativo (p=0.105).
20.8 Visualización de Modelos
A continuación, visualizaremos los coeficientes de ambos modelos de regresión con la función plot_models del paquete sjPlot.
- Modelo 1: Regresión de Poisson sin offset
- Modelo 2: Regresión de Poisson con offset
library(sjPlot)
plot_models(model_1, model_2, model_3, model_4,
m.labels = c("Poisson Individual sin Offset",
"Poisson Agrupada sin Offset",
"Poisson Individual con Offset",
"Poisson Agrupada con Offset")) +
scale_y_continuous(limits = c(0.5, 2)) +
theme_bw()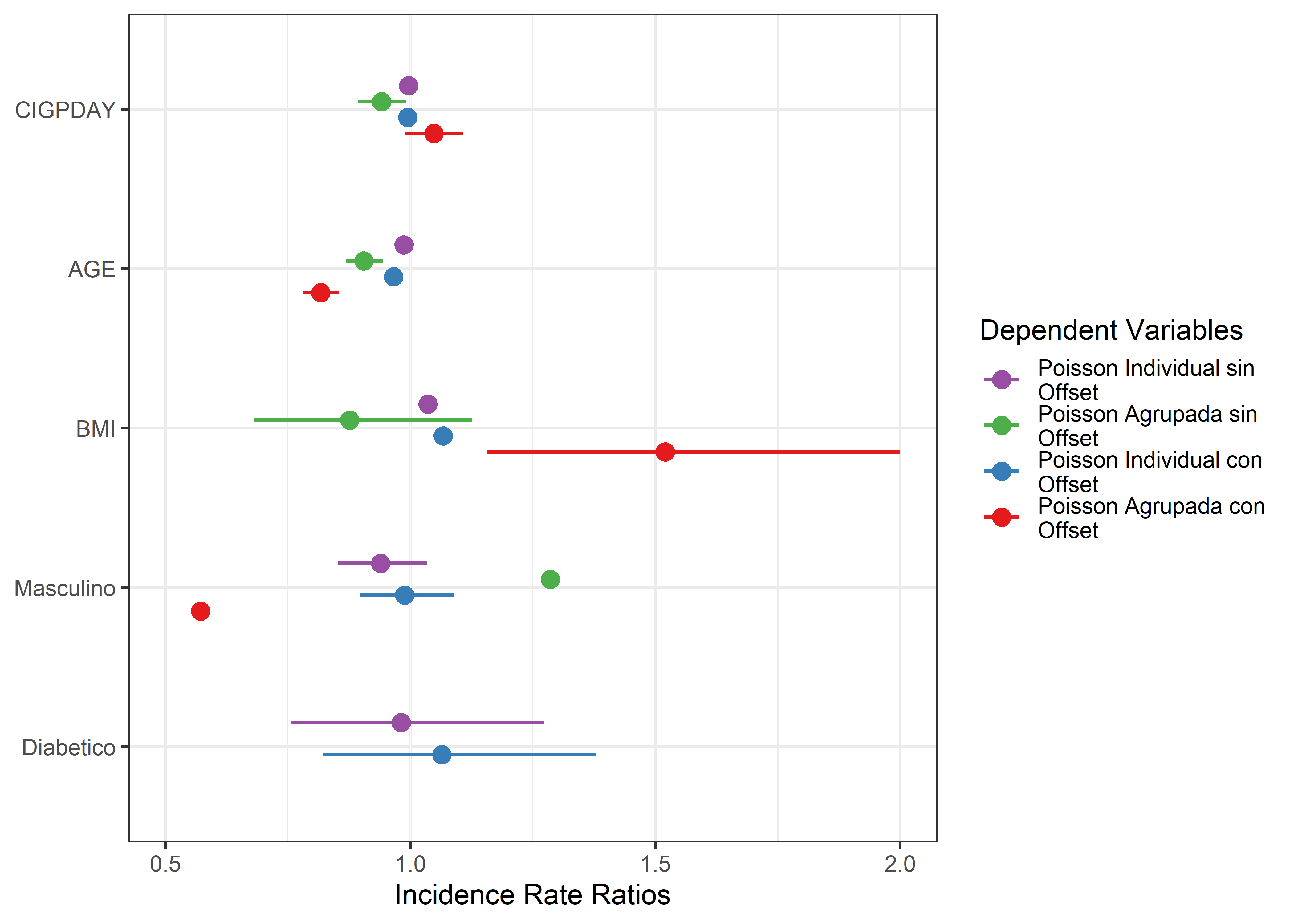
20.9 Sesgos en los estudios de cohortes
20.9.1 Sesgo de selección
La falta de respuesta y la no participación pueden introducir sesgos en los hallazgos del estudio. Es posible que las características de los participantes en la cohorte difieran significativamente de las de aquellos que optaron por no participar en el estudio. Por ejemplo, podría ocurrir que las personas que rechazaron participar en el estudio tengan una mayor probabilidad de ser fumadores en comparación con aquellos que decidieron participar. Además, es posible que los fumadores que no participaron tengan una mayor probabilidad de presentar alguna enfermedad en comparación con los que sí participaron, lo que podría sesgar la asociación hacia un valor nulo.
Adicionalmente, si las personas que se pierden durante el seguimiento difieren de aquellas que permanecen en el estudio, esto podría plantear un problema al calcular las tasas de incidencia, lo que, a su vez, podría afectar la estimación de la asociación.
20.9.2 Sesgo de información
Este sesgo surge cuando la información sobre la exposición no se recopila de manera precisa o es propensa a errores. Puede conducir a una clasificación errónea de los individuos en grupos expuestos y no expuestos, lo que distorsiona la relación entre la exposición y el resultado.
20.10 Ejercicios
20.10.1 Ejercicio 1
- Realizar un modelo de regresión de Poisson para estimar tasas individuales, considerando como desenlace a la variable casos de hipertensión
(HYPERTEN)y como covariables a edad(AGE), condición de fumador(CURSMOKE)y colesterol LDL(LDLC).
20.10.2 Ejercicio 2
- Visualice el modelo del ejercicio 1.