11 Contraste de variables categóricas
11.1 General
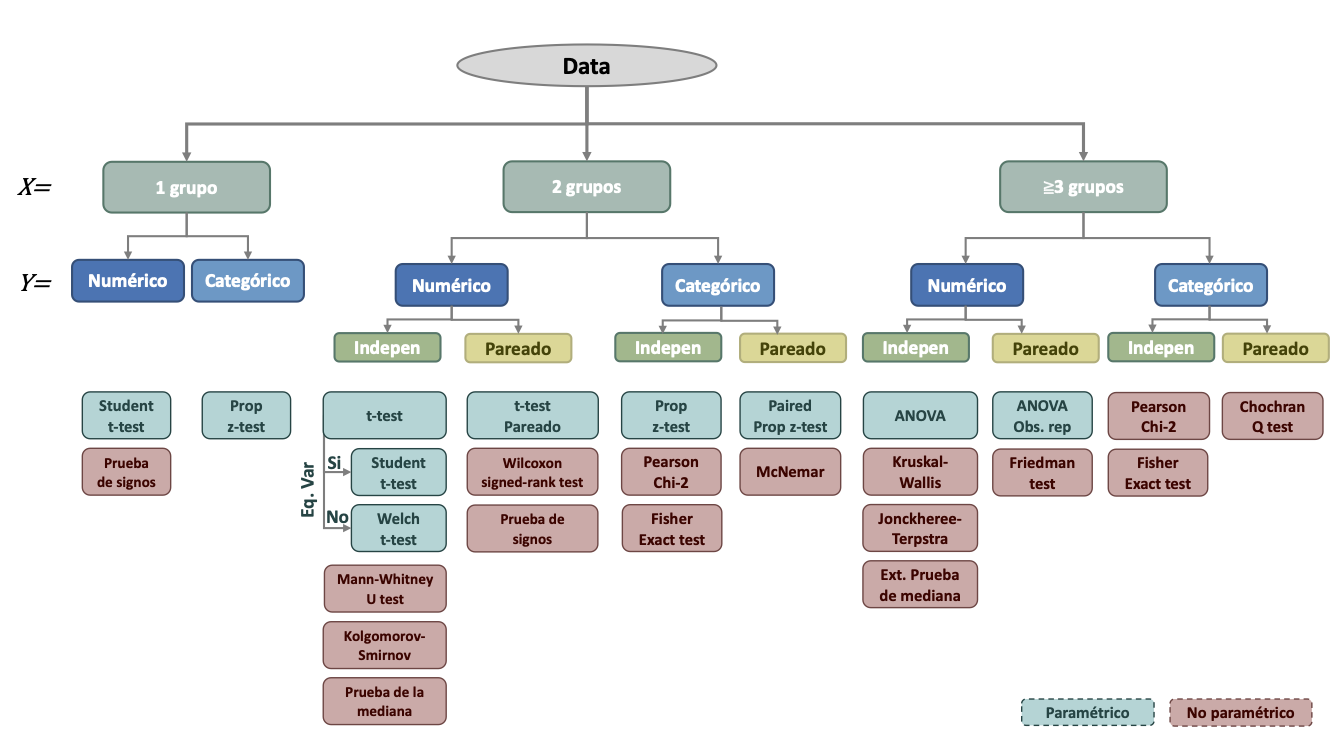
En esta sección, exploraremos múltiples funciones para hacer inferencia estadística. Estas pruebas se pueden dividir de acuerdo al número de grupos a comparar ( x ), al tipo (numérica o continua) de variable dependiente ( y ) y si las observaciones entre ambos grupos son independientes o relacionadas (pareadas). Usaremos este esquema general para organizar esta sección. Sin embargo, no representa una lista exhaustiva de todas las pruebas estadísticas disponibles en R y tampoco se abordarán todas las pruebas mencionadas.
11.2 Paquetes y Data
Los paquetes que se utilizarán son:
El archivo de datos dhs.csv contiene información relacionada a la salud materno-infantil y condiciones sociodemográficas en Perú. En este conjunto de datos, cada observación (una madre que tiene un hijo dentro del periodo de estudio) está agrupada en comunidades. Este conjunto de datos es una submuestra de la Encuesta Demográfica y de Salud Familiar (ENDES). Para esta sección, exploraremos algunos factores asociados a la muerte infantil en menores de 1 mes de nacidos (death_1m)
peru <- read_csv("data/dhs.csv")11.3 Medidas de Resumen
11.3.1 Tablas de frecuencias
Como se ha visto en secciones anteriores, el paquete janitor tiene la función tabyl que permite generar tablas de frecuencias y se integra en el ecosistema del tidyverse.
death_1m n percent valid_percent
0 13299 0.983581096 0.990835941
1 123 0.009096960 0.009164059
NA 99 0.007321944 NAObservamos que nuestro conjunto de datos tiene valores faltantes. Para motivos de esta práctica filtraremos todas las observaciones que contienen valores faltantes en alguna variable de nuestro conjunto de datos.
Para excluir observaciones de nuestro conjunto de datos, se debe primero hacer un análisis adecuado. Se debe revisar los mecanismos de generación de datos faltantes y si estos no afectan los análisis que se quieren realizar. Es importante reportar los criterios de exclusión de las observaciones al momento de publicar nuestro análisis.
Revisaremos nuestro nuevo conjunto de datos sin datos faltantes. Utilizaremos adorn_totals("row") para agregar el total de las filas y adorn_pct_formatting() para dar formato a la columna de porcentajes.
peru %>%
tabyl(death_1m) %>%
adorn_totals("row") %>%
adorn_pct_formatting()| death_1m | n | percent |
|---|---|---|
| 0 | 6585 | 99.0% |
| 1 | 65 | 1.0% |
| Total | 6650 | 100.0% |
11.3.2 Tablas de contingencia
Transformaremos nuestras variables de interés a factores.
Podemos realizar tablas de doble entrada (frecuencias de 2 variables) con tabyl.
| death_1m | No | Si |
|---|---|---|
| No | 2507 | 4078 |
| Si | 40 | 25 |
Al igual que con las frecuencias de una variable, podemos cambiar el formato de la tabla con adorn_*(). Podrán encontrar más información detallada de las opciones de formato en la documentación de janitor.
peru %>%
tabyl(death_1m, safe_water) %>%
adorn_percentages("col") %>%
adorn_pct_formatting(digits = 2) %>%
adorn_ns()| death_1m | No | Si |
|---|---|---|
| No | 98.43% (2,507) | 99.39% (4,078) |
| Si | 1.57% (40) | 0.61% (25) |
Otro paquete con funciones útiles para medidas descriptivas es pubh (enfocado en salud pública). La función cross_tbl() permite realizar también tablas de doble entrada.
|
No, N = 2,547 |
Si, N = 4,103 |
Overall, N = 6,650 |
|
|---|---|---|---|
| village | 1,050 (516, 1,566) | 1,003 (441, 1,542) | 1,011 (472, 1,551) |
| literacy | |||
| 0 = cannot read at all | 271 (11%) | 271 (6.6%) | 542 (8.2%) |
| 1 = able to read only parts of sentence | 150 (5.9%) | 176 (4.3%) | 326 (4.9%) |
| 2 = able to read whole sentence | 2,124 (83%) | 3,656 (89%) | 5,780 (87%) |
| 4 = blind/visually impaired | 2 (<0.1%) | 0 (0%) | 2 (<0.1%) |
| wealth_ind | |||
| 1 = poorest | 858 (34%) | 387 (9.4%) | 1,245 (19%) |
| 2 = poorer | 809 (32%) | 980 (24%) | 1,789 (27%) |
| 3 = middle | 617 (24%) | 1,115 (27%) | 1,732 (26%) |
| 4 = richer | 188 (7.4%) | 939 (23%) | 1,127 (17%) |
| 5 = richest | 75 (2.9%) | 682 (17%) | 757 (11%) |
| insurance | |||
| 0 = no | 1,189 (47%) | 1,838 (45%) | 3,027 (46%) |
| 1 = yes | 1,358 (53%) | 2,265 (55%) | 3,623 (54%) |
| age | 19.0 (17.0, 21.0) | 20.0 (17.0, 23.0) | 19.0 (17.0, 22.0) |
| partner_work | |||
| 0 = did not work | 0 (0%) | 6 (0.1%) | 6 (<0.1%) |
| 1 = prof., tech., manag. | 204 (8.0%) | 634 (15%) | 838 (13%) |
| 2 = clerical | 36 (1.4%) | 152 (3.7%) | 188 (2.8%) |
| 3 = sales | 162 (6.4%) | 270 (6.6%) | 432 (6.5%) |
| 4 = agric-self employed | 1,231 (48%) | 1,285 (31%) | 2,516 (38%) |
| 6 = household & domestic | 41 (1.6%) | 103 (2.5%) | 144 (2.2%) |
| 7 = services | 282 (11%) | 615 (15%) | 897 (13%) |
| 8 = skilled manual | 382 (15%) | 741 (18%) | 1,123 (17%) |
| 9 = unskilled manual | 203 (8.0%) | 295 (7.2%) | 498 (7.5%) |
| 99 | 6 (0.2%) | 2 (<0.1%) | 8 (0.1%) |
| partner_age | 32 (27, 38) | 34 (28, 39) | 33 (28, 39) |
| work | |||
| 0 = no | 784 (31%) | 1,334 (33%) | 2,118 (32%) |
| 1 = in the past year | 305 (12%) | 404 (9.8%) | 709 (11%) |
| 2 = currently working | 1,426 (56%) | 2,296 (56%) | 3,722 (56%) |
| 3 = have a job, but on leave last 7 days | 32 (1.3%) | 69 (1.7%) | 101 (1.5%) |
| decis_care | |||
| 0 | 1 (<0.1%) | 1 (<0.1%) | 2 (<0.1%) |
| 1 = respondent alone | 1,313 (52%) | 2,405 (59%) | 3,718 (56%) |
| 2 = respondent and husband/partner | 639 (25%) | 1,011 (25%) | 1,650 (25%) |
| 3 = respondent and other person | 8 (0.3%) | 14 (0.3%) | 22 (0.3%) |
| 4 = husband/partner alone | 574 (23%) | 642 (16%) | 1,216 (18%) |
| 5 = someone else | 12 (0.5%) | 30 (0.7%) | 42 (0.6%) |
| bw | 3,200 (2,850, 3,500) | 3,220 (2,900, 3,600) | 3,200 (2,900, 3,590) |
| num_child | |||
| 0 | 171 (6.7%) | 27 (0.7%) | 198 (3.0%) |
| 1 | 1,232 (48%) | 2,402 (59%) | 3,634 (55%) |
| 2 | 905 (36%) | 1,379 (34%) | 2,284 (34%) |
| 3 | 213 (8.4%) | 252 (6.1%) | 465 (7.0%) |
| 4 | 24 (0.9%) | 36 (0.9%) | 60 (0.9%) |
| 5 | 2 (<0.1%) | 5 (0.1%) | 7 (0.1%) |
| 6 | 0 (0%) | 1 (<0.1%) | 1 (<0.1%) |
| 7 | 0 (0%) | 1 (<0.1%) | 1 (<0.1%) |
| educ_yrs | 7.0 (5.0, 11.0) | 11.0 (6.0, 12.0) | 9.0 (6.0, 11.0) |
| death_1m | |||
| No | 2,507 (98%) | 4,078 (99%) | 6,585 (99%) |
| Si | 40 (1.6%) | 25 (0.6%) | 65 (1.0%) |
11.4 Visualización y AED
11.4.1 Frecuencias
Usaremos la geometría geom_bar() del paquete ggplot para generar un gráfico de barras de una variable (tabulación de un solo sentido).
En el siguiente ejemplo, exploraremos la variable Diet para visualizar la distribución de las frecuencias de dietas chow y hf.
11.4.2 Mosaicos
Los gráficos de mosaicos nos permiten comparar dos variables categóricas. Usaremos la geometría geom_mosaic() del paquete ggmosaic
peru %>%
ggplot() +
geom_mosaic(aes(x = product(safe_water, wealth_ind), fill = safe_water))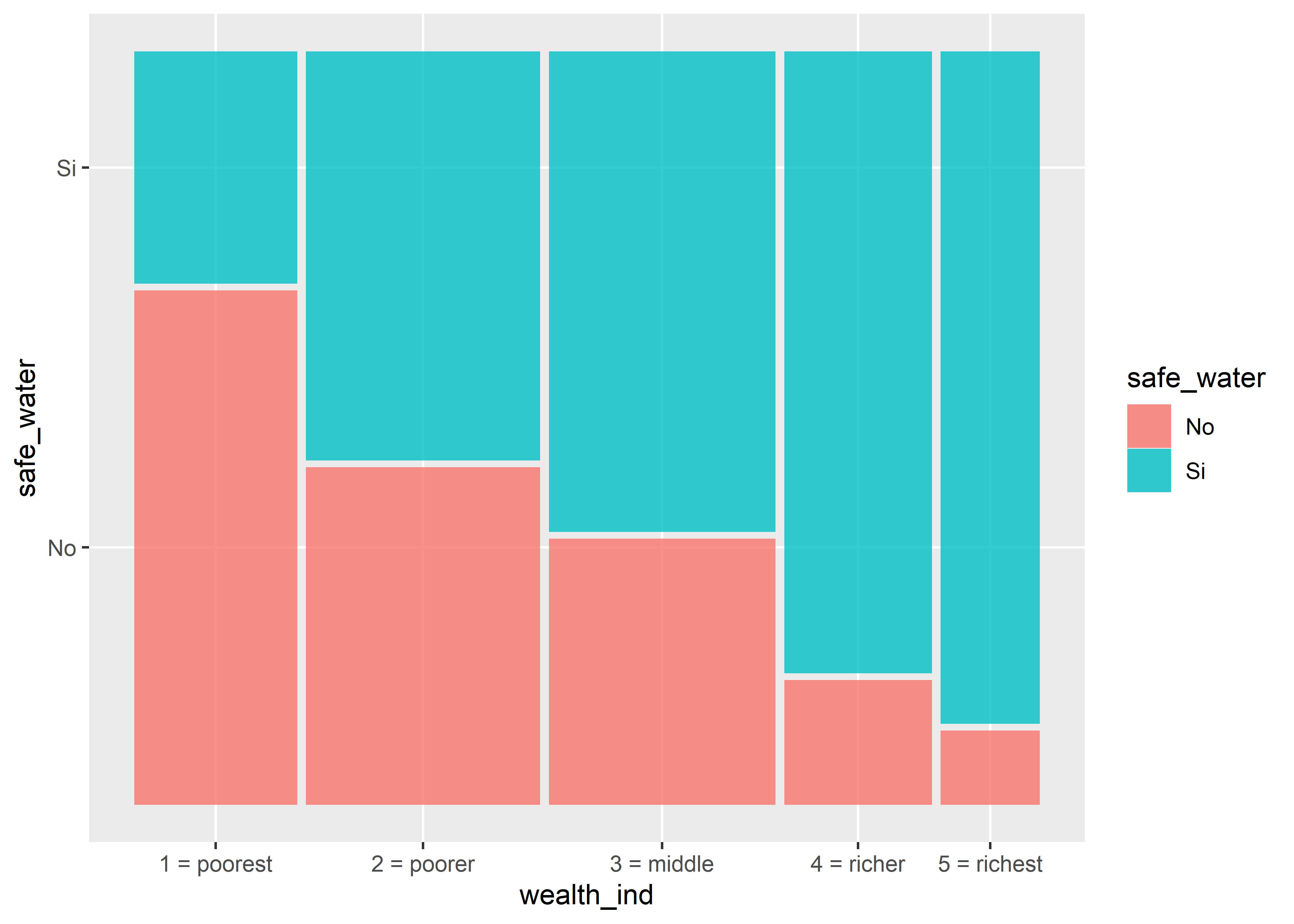
11.5 Pruebas de hipótesis
11.5.1 Chi2
11.5.1.1 Bondad de Ajuste (Goodness of fit)
Usaremos la prueba de chi-cuadrado con el paquete rstatix y las funciones chisq_test() para comparar los valores observados contra una probabilidad de referencia.
Si no se especifica la probabilidad de referencia,
chisq_test()utiliza un probabilidad homogénea entre las catagorías de la variable categórica. Para una variable binaria la probablidad usada es50%. Se puede especificar la probabilidad a ser analizada con el argumentop.
| n | statistic | p | df | method | p.signif |
|---|---|---|---|---|---|
| 2 | 6392.541 | 0 | 1 | Chi-square test | **** |
Podemos explorar a profundidad la prueba de chi-cuadrado con la función chisq_descriptives().
peru %>%
tabyl(death_1m) %>%
pull(n) %>%
chisq_test() %>%
chisq_descriptives() %>%
adorn_totals("row")| Var1 | observed | prop | expected | resid | std.resid |
|---|---|---|---|---|---|
| A | 6585 | 0.9902256 | 3325 | 56.53557 | 79.95337 |
| B | 65 | 0.0097744 | 3325 | -56.53557 | -79.95337 |
| Total | 6650 | 1.0000000 | 6650 | 0.00000 | 0.00000 |
El valor del estadístico de chi-cuadrado de Pearson es la suma de los residuos elevados al cuadrado.
chi2_summ <- peru %>%
tabyl(death_1m) %>%
pull(n) %>%
chisq_test() %>%
chisq_descriptives()
sum(chi2_summ$resid^2)[1] 6392.541También se puede usar la función goodnessOfFitTest() del paquete lsr
Chi-square test against specified probabilities
Data variable: .
Hypotheses:
null: true probabilities are as specified
alternative: true probabilities differ from those specified
Descriptives:
observed freq. expected freq. specified prob.
No 6585 3325 0.5
Si 65 3325 0.5
Test results:
X-squared statistic: 6392.541
degrees of freedom: 1
p-value: <.001 11.5.1.2 Independencia
Primero, creamos la tabla de contingencia que vamos a analizar.
| death_1m | No | Si |
|---|---|---|
| No | 2507 | 4078 |
| Si | 40 | 25 |
El paquete janitor tiene una extensión de la función chisq.test() para usar en objetos de clase tabyl.
chisq.test(tab1, cor = F)
Pearson's Chi-squared test
data: tab1
X-squared = 15, df = 1, p-value = 0.0001075Podemos también usar la función chisq_test() del paquete rstatix.
tab1 %>%
column_to_rownames("death_1m") %>%
chisq_test(cor = F)| n | statistic | p | df | method | p.signif |
|---|---|---|---|---|---|
| 6650 | 14.99957 | 0.000108 | 1 | Chi-square test | *** |
Podemos explorar a profundidad la prueba de chi-cuadrado con el paquete rstatix y la función chisq_descriptives()
chi2_summ <- tab1 %>%
column_to_rownames("death_1m") %>%
chisq_test(cor = F) %>%
chisq_descriptives()| Var1 | Var2 | observed | prop | row.prop | col.prop | expected | resid | std.resid |
|---|---|---|---|---|---|---|---|---|
| No | No | 2507 | 0.3769925 | 0.3807137 | 0.9842952 | 2522.10451 | -0.3007635 | -3.872927 |
| Si | No | 40 | 0.0060150 | 0.6153846 | 0.0157048 | 24.89549 | 3.0272365 | 3.872927 |
| No | Si | 4078 | 0.6132331 | 0.6192863 | 0.9939069 | 4062.89549 | 0.2369675 | 3.872927 |
| Si | Si | 25 | 0.0037594 | 0.3846154 | 0.0060931 | 40.10451 | -2.3851191 | -3.872927 |
El valor del estadístico de chi-cuadrado de Pearson es la suma de los residuos elevados al cuadrado.
sum(chi2_summ$resid^2)[1] 14.9995711.5.2 Fisher
El paquete janitor tiene una extensión de la función fisher.test() para usar en objetos de clase tabyl.
fisher.test(tab1)
Fisher's Exact Test for Count Data
data: tab1
p-value = 0.0001619
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.2228505 0.6509724
sample estimates:
odds ratio
0.3842822 Podemos también usar la función fisher_test() del paquete rstatix.
tab1 %>%
column_to_rownames("death_1m") %>%
fisher_test()| n | p | p.signif |
|---|---|---|
| 6650 | 0.000162 | *** |
11.6 Tablas epidemiológicas
También podemos usar la función contingency() del paquete pubh para generar una salida de datos más completa.
peru %>%
contingency(death_1m ~ safe_water) Outcome
Predictor Si No
Si 25 4078
No 40 2507
Outcome + Outcome - Total Inc risk *
Exposed + 25 4078 4103 0.61 (0.39 to 0.90)
Exposed - 40 2507 2547 1.57 (1.12 to 2.13)
Total 65 6585 6650 0.98 (0.76 to 1.24)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Inc risk ratio 0.39 (0.24, 0.64)
Inc odds ratio 0.38 (0.23, 0.63)
Attrib risk in the exposed * -0.96 (-1.50, -0.42)
Attrib fraction in the exposed (%) -157.75 (-323.78, -56.76)
Attrib risk in the population * -0.59 (-1.13, -0.06)
Attrib fraction in the population (%) -60.67 (-94.60, -32.66)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 15.000 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
Wald confidence limits
CI: confidence interval
* Outcomes per 100 population units
Pearson's Chi-squared test with Yates' continuity correction
data: dat
X-squared = 14.023, df = 1, p-value = 0.0001806Otro paquete útil para mostrar múltiples pruebas de hipótesis es table2x2() del paquete Publish.
tab1 %>%
column_to_rownames("death_1m") %>%
table2x2()_____________________________
2x2 contingency table
_____________________________
No Si Sum
No 2507 4078 6585
Si 40 25 65
-- -- -- --
Sum 2547 4103 6650
_____________________________
Statistics
_____________________________
a= 2507
b= 4078
c= 40
d= 25
p1=a/(a+b)= 0.3807
p2=c/(c+d)= 0.6154
_____________________________
Risk difference
_____________________________
Risk difference = RD = p1-p2 = -0.2347
Standard error = SE.RD = sqrt(p1*(1-p1)/(a+b)+p2*(1-p2)/(c+d)) = 0.06064
Lower 95%-confidence limit: = RD - 1.96 * SE.RD = -0.3535
Upper 95%-confidence limit: = RD + 1.96 * SE.RD = -0.1158
The estimated risk difference is -23.5% (CI_95%: [-35.4;-11.6]).
_____________________________
Risk ratio
_____________________________
Risk ratio = RR = p1/p2 = 0.6187
Standard error = SE.RR = sqrt((1-p1)/a+(1-p2)/c)= 0.09931
Lower 95%-confidence limit: = RR * exp(- 1.96 * SE.RR) = 0.5092
Upper 95%-confidence limit: = RR * exp(1.96 * SE.RR) = 0.7516
The estimated risk ratio is 0.619 (CI_95%: [0.509;0.752]).
_____________________________
Odds ratio
_____________________________
Odds ratio = OR = (p1/(1-p1))/(p2/(1-p2)) = 0.3842
Standard error = SE.OR = sqrt((1/a+1/b+1/c+1/d)) = 0.2562
Lower 95%-confidence limit: = OR * exp(- 1.96 * SE.OR) = 0.2325
Upper 95%-confidence limit: = OR * exp(1.96 * SE.OR) = 0.6349
The estimated odds ratio is 0.384 (CI_95%: [0.233;0.635]).
_____________________________
Chi-square test
_____________________________
Pearson's Chi-squared test with Yates' continuity correction
data: table2x2
X-squared = 14.023, df = 1, p-value = 0.0001806
_____________________________
Fisher's exact test
_____________________________
Fisher's Exact Test for Count Data
data: table2x2
p-value = 0.0001619
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.2228505 0.6509724
sample estimates:
odds ratio
0.3842822 11.7 Ejercicios
Para estos, ejercicios usaremos el conjunto de datos birthwt del paquete MASS.
Rows: 189
Columns: 10
$ low <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ age <int> 19, 33, 20, 21, 18, 21, 22, 17, 29, 26, 19, 19, 22, 30, 18, 18, …
$ lwt <int> 182, 155, 105, 108, 107, 124, 118, 103, 123, 113, 95, 150, 95, 1…
$ race <int> 2, 3, 1, 1, 1, 3, 1, 3, 1, 1, 3, 3, 3, 3, 1, 1, 2, 1, 3, 1, 3, 1…
$ smoke <int> 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0…
$ ptl <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0…
$ ht <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ ui <int> 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1…
$ ftv <int> 0, 3, 1, 2, 0, 0, 1, 1, 1, 0, 0, 1, 0, 2, 0, 0, 0, 3, 0, 1, 2, 3…
$ bwt <int> 2523, 2551, 2557, 2594, 2600, 2622, 2637, 2637, 2663, 2665, 2722…Este conjunto de datos contiene 189 observaciones para analizar factores de riesgo asociados al bajo peso de infantes al nacer. La variable low es el indicador de un peso al nacer menor que 2.5 kg. age es la edad de la madre en años, lwt es el peso de la madre en libras en el último periodo menstrual, race es la raza de la madre, smoke es el tabaquismo durante el embarazo, plt es el número de partos prematuros previos, ht es el historial de hipertensión, ui es la presencia de irritabilidad uterina, ftv es el número de visitas médicas durante el primer trimestre, y bwt es el peso en gramos al nacer.
Ejercicio 1
Realizar un análisis exploratorio para evaluar descriptivamente la asociación entre el indicador de bajo peso al nacer y el tabaquismo durante el embarazo y la raza de la madre. Crear tablas de contigencia y visualizaciones para cada caso.
Ejercicio 2
Evaluar la significancia de la asociación entre el indicador de bajo peso al nacer y el tabaquismo durante el embarazo y la raza de la madre. Usar las dos pruebas vistas en este capítulo.