15 Regresión logística: Evaluación y extensiones
En este capítulos veremos algunas herramientas y análisis adicionales concernientes a los modelos logísticos. Continuaremos usando los mismos datos:
15.1 Diagnóstico del modelo
15.1.1 General
Para generar gráficos de diagnóstico de modelos de regresión logística, podemos usar la función check_model() del paquete performance, que pertenece a la colección de paquetes easystats:
library(performance)
lrm_0 <- glm(diabetes ~ ., family = binomial, data = dm_data)
check_model(lrm_0)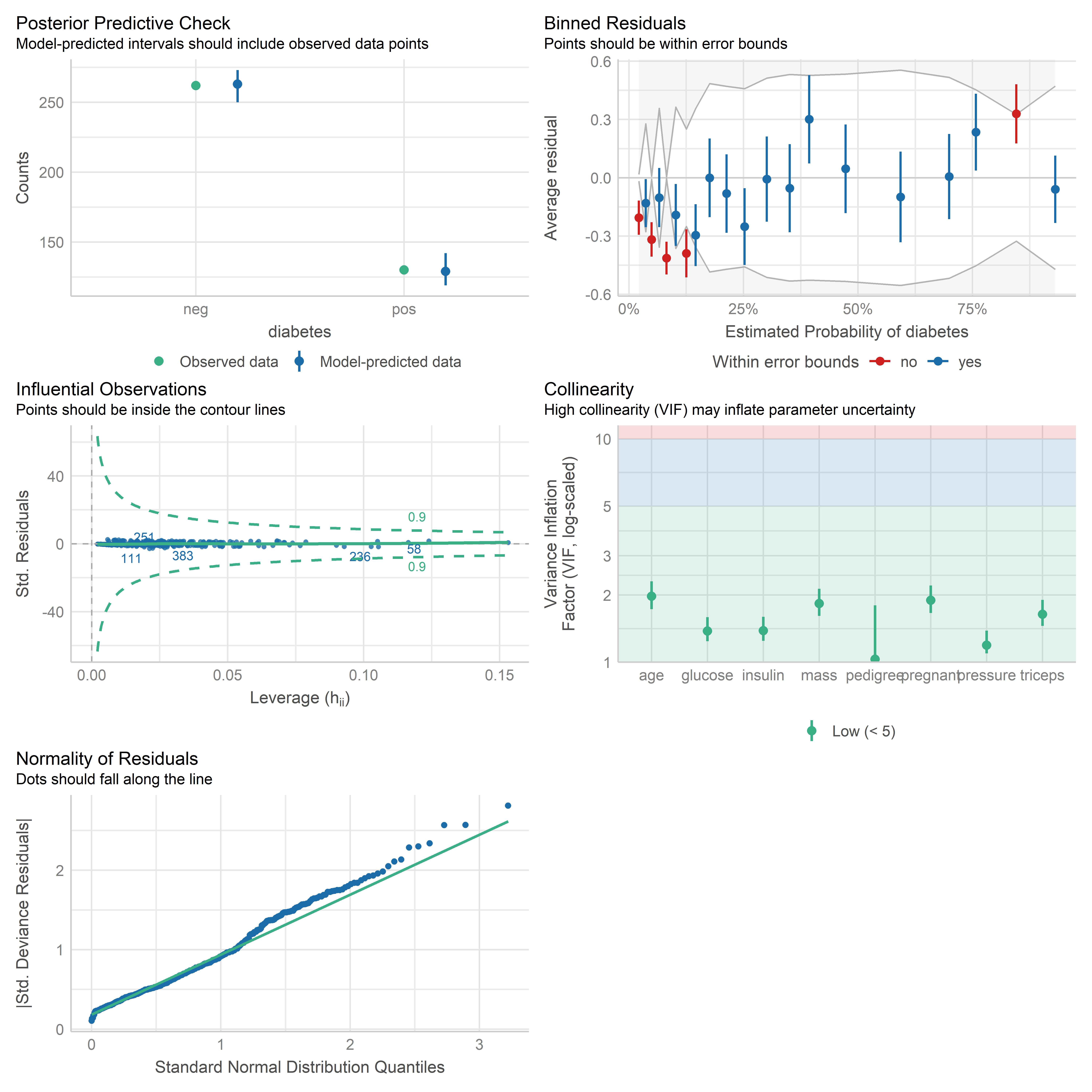
Esta función utiliza los residuales de Pearson estandarizados para elaborar los gráficos. Hay que tener en cuenta que estos residuales son adecuados solo cuando el número de observaciones es grande, ya que están basados en una aproximación normal. En otro caso, es mejor investigar los residuales de devianza.
Los gráficos que se muestran son los siguientes:
- Posterior Predictive Check: Nos indica qué tan bien el modelo predice la data observada usando simulaciones de la data bajo el modelo ajustado.
- Binned Residuals: Agrupa los residuales según diferentes niveles de la probabilidad estimada y calcula el promedio en cada grupo. Estos promedios no deberían salir de las bandas de error. En este caso no se aprecian los puntos que están dentro de las bandas (azules). Si esto pasara, podemos construir gráficos individuales para cada predictor.
- Influential Observations: Muestra posibles observaciones influyentes. Las observaciones no deberían sobrepasar los contornos.
- Collinearity: Muestra los valores del factor de inflación de la varianza (VIF) para los predictores.
- Normality of Residuals: No es tan relevante para los modelos de regresión logística, ya que no se asume normalidad de errores. Sin embargo, sirve de referencia para evaluar la distribución de los residuales.
Lo que más podemos rescatar de estos gráficos es la presencia de residuales bastante grandes. Si bien el gráfico de Posterior Predictive Check muestra que en general hay una concordancia entre la distribución de la variable de respuesta y las predicciones de la data, la presencia de residuales demasiado grandes nos indica que el modelo no está ajustando bien para algunas observaciones.
15.1.2 Bondad de ajuste
Si un modelo de regresión logística tiene un buen ajuste, se esperaría que las probabilidades predichas del modelo coincidan en distribución con las proporciones observadas de la variable de respuesta. Una prueba de significancia para verificar esto es la prueba de Hosmer-Lemeshow. La prueba a contrastar es que no hay asociación entre las probabilidades predichas y las proporciones observadas, lo cual indicaría una falta de ajuste.
Una implementación de esta prueba se encuentra en la función performance_hosmer() del paquete performance:
performance_hosmer(lrm_0)# Hosmer-Lemeshow Goodness-of-Fit Test
Chi-squared: 3.013
df: 8
p-value: 0.934Vemos que el p-valor es bastante grande, por lo que no hay evidencia para decir que no hay concordancia entre las probabilidades predichas y las proporciones observadas. Es decir, no hay evidencia para decir que no hay buen ajuste. Sin embargo, esto no quiere decir que necesariamente el modelo ajusta bien, solo que no se puede decir lo contrario.
15.1.3 Especificación de los términos
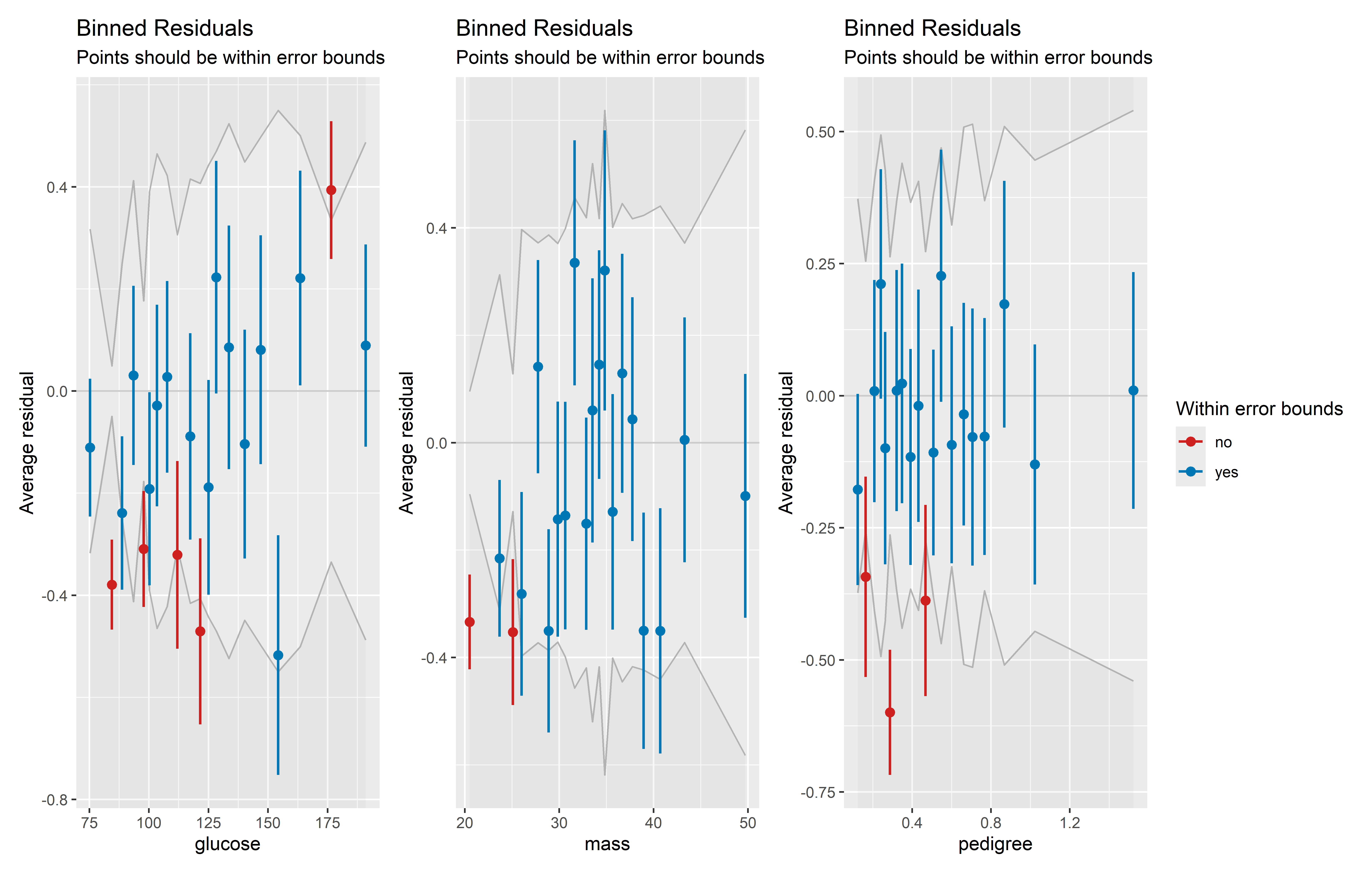
Podemos generar gráficos de binned residuals para cada predictor para detectar en qué niveles de estos hay residuales grandes en promedio. Además, un patrón no lineal muy evidente de los residuales promedios podría indicar una mala especificación del predictor.
Veamos los gráficos para las variables glucose, mass, pedigree y age, que resultaron significativos en el modelo. Primero obtengamos los gráficos individuales usando la función binned_residuals() y especificando el predictor en el parámetro term:
binned_glucose <- plot(binned_residuals(lrm_0, term = "glucose"))
binned_mass <- plot(binned_residuals(lrm_0, term = "mass"))
binned_pedigree <- plot(binned_residuals(lrm_0, term = "pedigree"))Ahora, usemos la función wrap_plots() del paquete patchwork para juntar los gráficos en uno solo. Incluiremos los argumentos ncol = 2 y nrow = 2 para que hayan dos filas y dos columnas de gráficos, y el argumento guides = "collect" para que coleccione las leyendas y muestre solo una:
library(patchwork)
wrap_plots(
binned_glucose, binned_mass, binned_pedigree, ncol = 3, nrow = 1,
guides = "collect"
)
Una mejor forma de analizar si existe un una mala especificación de un predictor en el modelo es usando gráficos de efectos marginales junto con residuales parciales. Los efectos marginales son valores predichos de la respuesta que se calculan al margen de los valores o niveles de un predictor específico, es decir, manteniendo constantes los valores o niveles de los demás predictores en el modelo. Por otro lado, los residuales parciales de un predictor son residuales que se calculan luego de haber “retirado” el efecto de las otros predictores en el modelo. Por lo tanto, son ideales para identificar si es que la asociación entre la variable de respuesta y un predictor se está capturando correctamente en el modelo.
Para calcular los efectos marginales de un predictor, podemos usar la función ggpredict() del paquete ggeffects. A esta función le pasamos el modelo y el predictor para el cual queremos calcular los efectos marginales. Para especificar el predictor usamos el parámetro terms y añandimos [all] al nombre del predictor para que se calculen los valores predichos para todos los valores del predictor. Por ejemplo, veamos para glucose:
Esta función nos devuelve los valores predichos (efectos marginales) y los valores para los cuales se han mantenido constantes los demás predictores.
Para generar el gráfico de efectos marginales, simplemente usamos la función plot() sobre el objeto que contiene las predicciones:
plot(pred_glucose)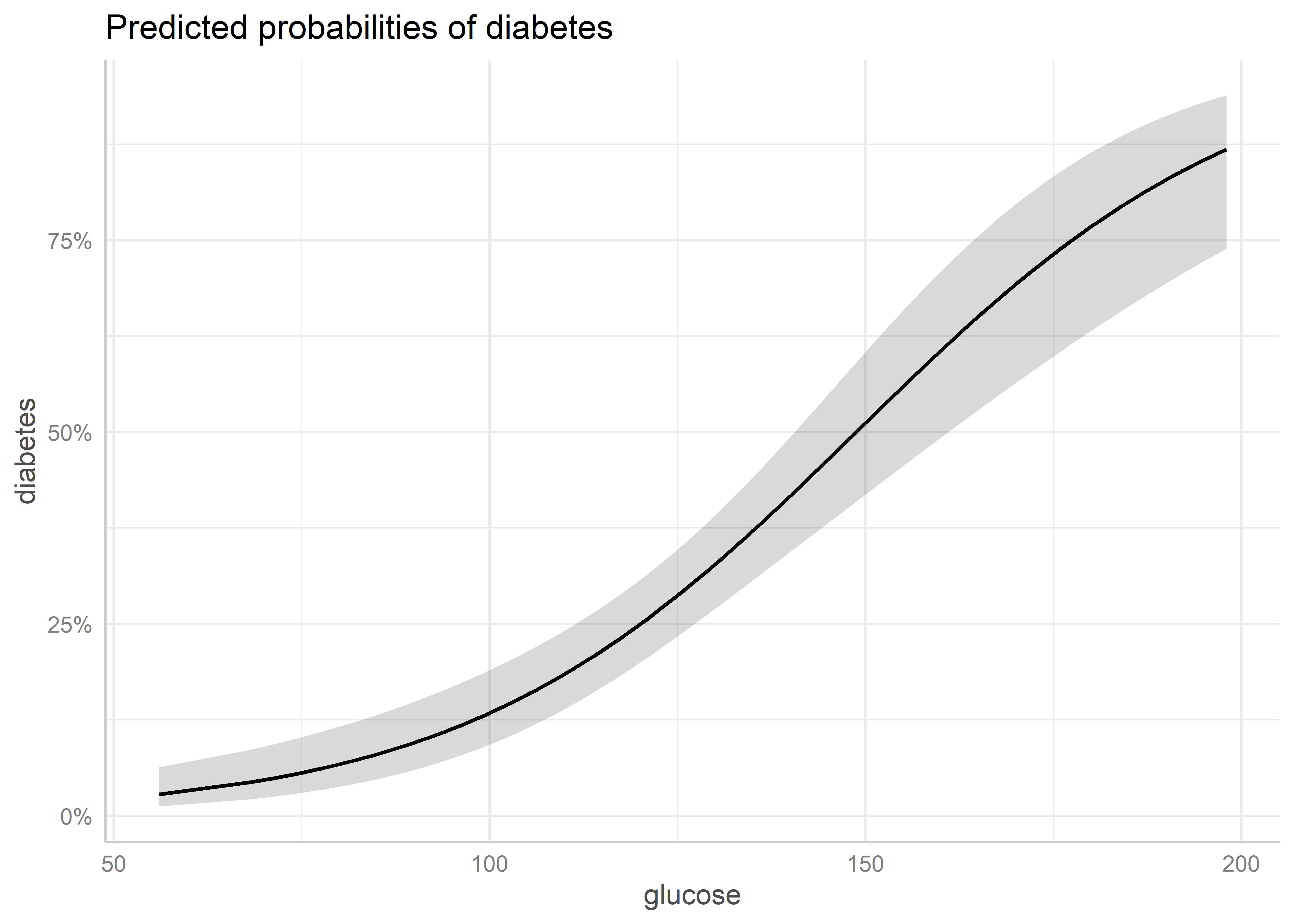
Agregaremos ahora los argumentos residuals = TRUE y residuals.line = TRUE para que se grafiquen los residuales parciales y una curva de tendencia para ellos:
plot_pred_glucose <- plot(pred_glucose, residuals = TRUE, residuals.line = TRUE)
plot_pred_glucose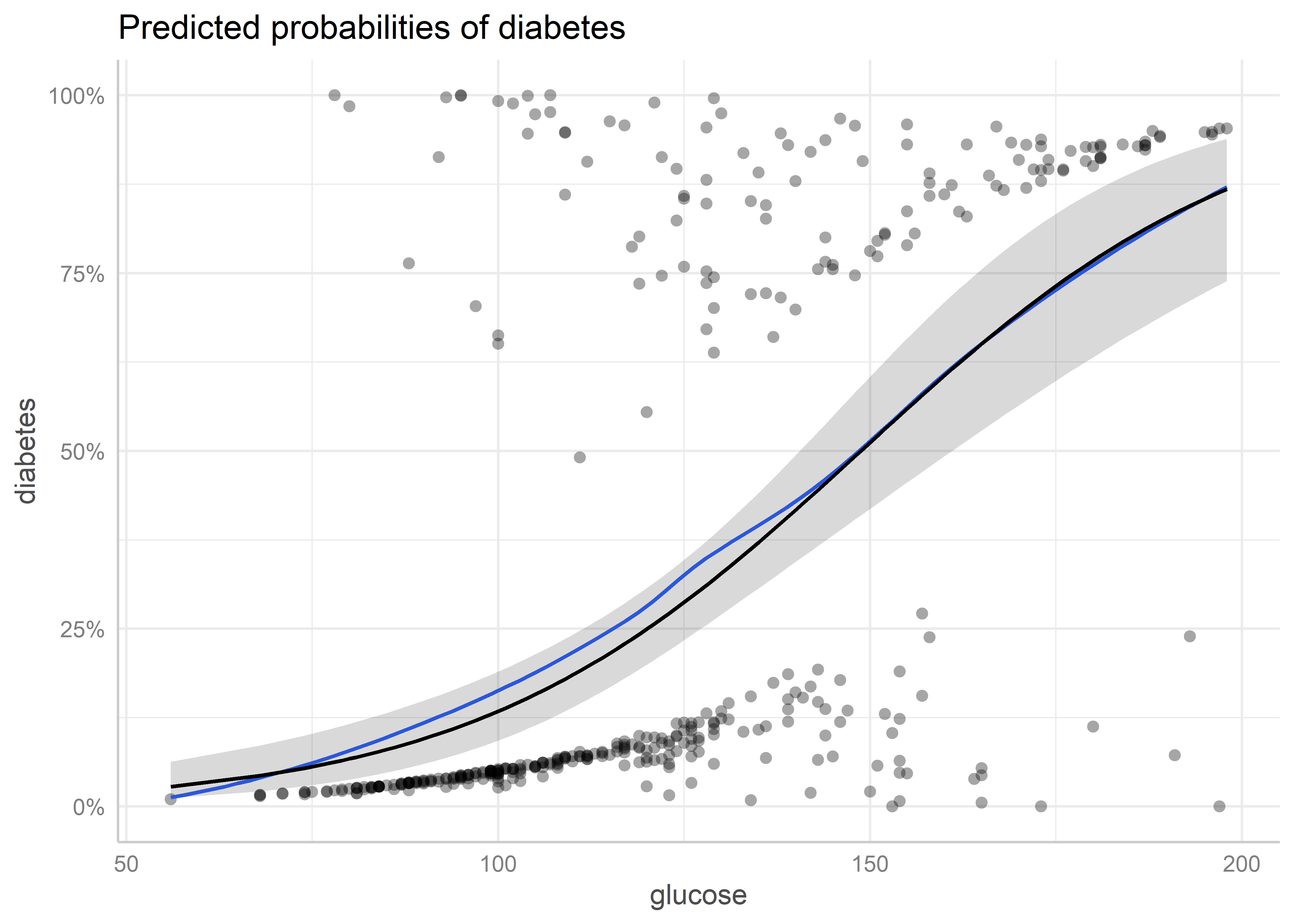
A mayor discrepancia entre la curva de tendencia de los residuales parciales y la curva de los efectos marginales, mayor evidencia de que el predictor puede estar mal especificado en el modelo. En este caso, vemos que no existe mucha discrepancia.
Veamos los gráficos para mass, pedigree y age:
pred_mass <- ggpredict(lrm_0, terms = "mass [all]")
pred_pedigree <- ggpredict(lrm_0, terms = "pedigree [all]")
pred_age <- ggpredict(lrm_0, terms = "age [all]")
plot_pred_mass <- plot(pred_mass, residuals = TRUE, residuals.line = TRUE)Data points may overlap. Use the `jitter` argument to add some amount of
random variation to the location of data points and avoid overplotting.plot_pred_pedigree <- plot(pred_pedigree, residuals = TRUE, residuals.line = TRUE)Data points may overlap. Use the `jitter` argument to add some amount of
random variation to the location of data points and avoid overplotting.plot_pred_age <- plot(pred_age, residuals = TRUE, residuals.line = TRUE)Data points may overlap. Use the `jitter` argument to add some amount of
random variation to the location of data points and avoid overplotting.Ahora, juntemos todos:
wrap_plots(
plot_pred_glucose, plot_pred_mass, plot_pred_pedigree, plot_pred_age,
ncol = 2, nrow = 2, guides = "collect"
)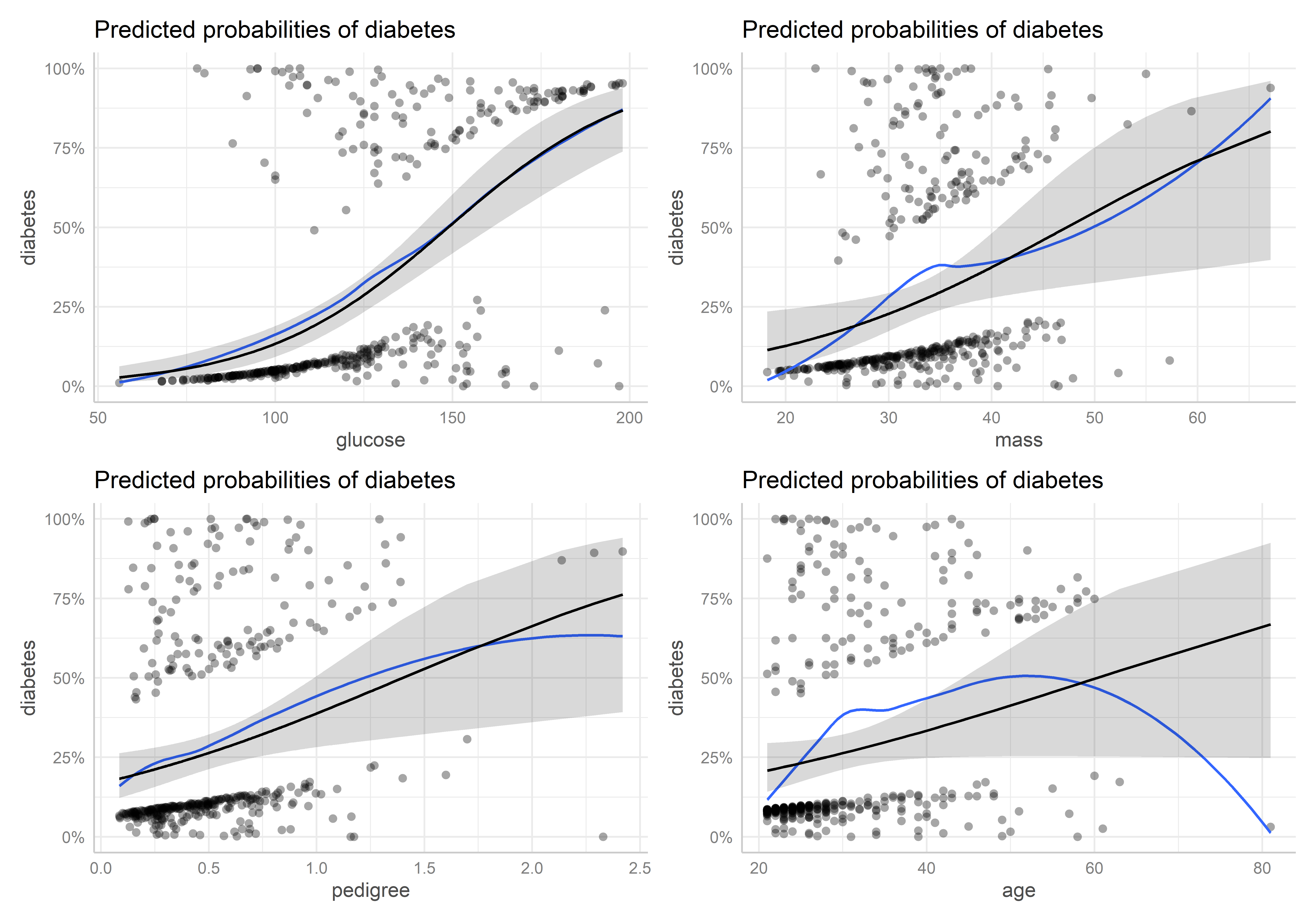
En los gráficos de las variables mass, pedigree y age se evidencia que existen valores extremos que distorsionan o fuerzan demasiado los efectos marginales de estos predictores y, por tanto, su asociación con la variable de respuesta en el modelo. Esto pone en tela de juicio los efectos significativos encontrados para estos predictores en el modelo. La magnitud de estos valores extremos nos hace pensar que tal vez estas variables no se han recolectado correctamente o ha habido mucho error en las mediciones, entre otras cosas.
15.2 Modelos anidados
Al igual que en el análisis de regresión lineal, podemos usar la función anova() para generar una tabla de significancia de los modelos anidados. Usemos los modelos lrm_3, lrm_4 y lrm_5:
lrm_2 <- glm(diabetes ~ ., family = binomial, data = dm_std)
lrm_3 <- glm(
diabetes ~ glucose + mass + pedigree + age,
family = binomial, data = dm_std
)
lrm_4 <- glm(
diabetes ~ glucose*mass + pedigree + age,
family = binomial, data = dm_std
)
anova(lrm_2, lrm_3, lrm_4, test = "Chisq")Analysis of Deviance Table
Model 1: diabetes ~ pregnant + glucose + pressure + triceps + insulin +
mass + pedigree + age
Model 2: diabetes ~ glucose + mass + pedigree + age
Model 3: diabetes ~ glucose * mass + pedigree + age
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 383 344.02
2 387 347.23 -4 -3.2138 0.5227
3 386 344.80 1 2.4349 0.1187Vemos que no existen diferencias estadísticamente significativas entre el modelo lrm_3 sobre lrm_2 y tampoco de lrm_4 sobre lrm_3.
15.3 Selección de variables
Para realizar la selección por pasos, podemos usar la función stepAIC() del paquete MASS:
Esta función utiliza el Akaike information criterion (AIC) para seleccionar el mejor modelo.
15.3.0.1 Búsqueda hacia adelante
Para realizar la búsqueda hacia adelante con stepAIC(), tenemos que primero crear el modelo nulo que servirá como modelo inicial para la función:
lrm_null <- glm(diabetes ~ 1, family = binomial, data = dm_std)Luego, en la función stepAIC() añadimos el argumento direction = "forward" y en scope definimos el rango de modelos que queremos probar:
lrm_forward <- stepAIC(
lrm_null, direction = "forward",
scope = list(lower = diabetes ~ 1, upper = diabetes ~ glucose * mass * pedigree * age)
)Start: AIC=500.1
diabetes ~ 1
Df Deviance AIC
+ glucose 1 386.67 390.67
+ age 1 450.67 454.67
+ mass 1 469.03 473.03
+ pedigree 1 481.37 485.37
<none> 498.10 500.10
Step: AIC=390.67
diabetes ~ glucose
Df Deviance AIC
+ age 1 370.69 376.69
+ mass 1 372.12 378.12
+ pedigree 1 376.34 382.34
<none> 386.67 390.67
Step: AIC=376.69
diabetes ~ glucose + age
Df Deviance AIC
+ mass 1 354.37 362.37
+ pedigree 1 361.73 369.73
<none> 370.69 376.69
+ glucose:age 1 370.17 378.17
Step: AIC=362.37
diabetes ~ glucose + age + mass
Df Deviance AIC
+ pedigree 1 347.23 357.23
<none> 354.37 362.37
+ glucose:mass 1 352.76 362.76
+ mass:age 1 353.55 363.55
+ glucose:age 1 354.27 364.27
Step: AIC=357.23
diabetes ~ glucose + age + mass + pedigree
Df Deviance AIC
+ glucose:pedigree 1 340.80 352.80
+ glucose:mass 1 344.80 356.80
<none> 347.23 357.23
+ mass:pedigree 1 345.75 357.75
+ mass:age 1 346.50 358.50
+ pedigree:age 1 347.06 359.06
+ glucose:age 1 347.18 359.18
Step: AIC=352.8
diabetes ~ glucose + age + mass + pedigree + glucose:pedigree
Df Deviance AIC
<none> 340.80 352.80
+ glucose:mass 1 339.04 353.04
+ mass:age 1 339.99 353.99
+ mass:pedigree 1 340.49 354.49
+ glucose:age 1 340.60 354.60
+ pedigree:age 1 340.64 354.64Para ver los resultados del ajuste usamos la función summary():
summary(lrm_forward)
Call:
glm(formula = diabetes ~ glucose + age + mass + pedigree + glucose:pedigree,
family = binomial, data = dm_std)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.0249 0.1465 -6.996 2.63e-12 ***
glucose 1.1883 0.1608 7.390 1.47e-13 ***
age 0.5373 0.1389 3.869 0.000109 ***
mass 0.5533 0.1448 3.822 0.000132 ***
pedigree 0.4787 0.1399 3.423 0.000620 ***
glucose:pedigree -0.3224 0.1164 -2.769 0.005620 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 498.1 on 391 degrees of freedom
Residual deviance: 340.8 on 386 degrees of freedom
AIC: 352.8
Number of Fisher Scoring iterations: 5En este caso, el algoritmo selecciona el modelo con solo los efectos principales de glucose, age, mass, pedigree y la interacción entre glucose y pedigree.
15.3.0.2 Búsqueda hacia atrás
Para realizar la búsqueda hacia atrás, primero tenemos que construir el modelo completo:
lrm_full <- glm(
diabetes ~ glucose * mass * pedigree * age, family = binomial, data = dm_std
)Para hacer la selección para atrás necesitamos incluir direction = "backward":
lrm_backward <- stepAIC(
lrm_full, direction = "backward",
scope = list(lower = diabetes ~ 1, upper = diabetes ~ glucose * mass * pedigree * age)
)Start: AIC=358.35
diabetes ~ glucose * mass * pedigree * age
Df Deviance AIC
- glucose:mass:pedigree:age 1 328.29 358.29
<none> 326.35 358.35
Step: AIC=358.29
diabetes ~ glucose + mass + pedigree + age + glucose:mass + glucose:pedigree +
mass:pedigree + glucose:age + mass:age + pedigree:age + glucose:mass:pedigree +
glucose:mass:age + glucose:pedigree:age + mass:pedigree:age
Df Deviance AIC
- glucose:mass:age 1 328.43 356.43
- glucose:mass:pedigree 1 328.70 356.70
<none> 328.29 358.29
- glucose:pedigree:age 1 331.40 359.40
- mass:pedigree:age 1 331.70 359.70
Step: AIC=356.43
diabetes ~ glucose + mass + pedigree + age + glucose:mass + glucose:pedigree +
mass:pedigree + glucose:age + mass:age + pedigree:age + glucose:mass:pedigree +
glucose:pedigree:age + mass:pedigree:age
Df Deviance AIC
- glucose:mass:pedigree 1 328.94 354.94
<none> 328.43 356.43
- glucose:pedigree:age 1 331.40 357.40
- mass:pedigree:age 1 331.73 357.73
Step: AIC=354.94
diabetes ~ glucose + mass + pedigree + age + glucose:mass + glucose:pedigree +
mass:pedigree + glucose:age + mass:age + pedigree:age + glucose:pedigree:age +
mass:pedigree:age
Df Deviance AIC
- glucose:mass 1 330.71 354.71
<none> 328.94 354.94
- glucose:pedigree:age 1 331.77 355.77
- mass:pedigree:age 1 332.74 356.74
Step: AIC=354.71
diabetes ~ glucose + mass + pedigree + age + glucose:pedigree +
mass:pedigree + glucose:age + mass:age + pedigree:age + glucose:pedigree:age +
mass:pedigree:age
Df Deviance AIC
<none> 330.71 354.71
- glucose:pedigree:age 1 334.13 356.13
- mass:pedigree:age 1 334.39 356.39Veamos el resumen:
summary(lrm_backward)
Call:
glm(formula = diabetes ~ glucose + mass + pedigree + age + glucose:pedigree +
mass:pedigree + glucose:age + mass:age + pedigree:age + glucose:pedigree:age +
mass:pedigree:age, family = binomial, data = dm_std)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.0325 0.1491 -6.923 4.41e-12 ***
glucose 1.2438 0.1674 7.430 1.09e-13 ***
mass 0.6396 0.1520 4.208 2.58e-05 ***
pedigree 0.5630 0.1487 3.786 0.000153 ***
age 0.6163 0.1582 3.895 9.83e-05 ***
glucose:pedigree -0.3498 0.1270 -2.756 0.005859 **
mass:pedigree -0.1879 0.1454 -1.292 0.196348
glucose:age 0.1074 0.1919 0.560 0.575535
mass:age 0.3003 0.1672 1.796 0.072508 .
pedigree:age 0.1180 0.1860 0.634 0.525890
glucose:pedigree:age -0.3227 0.1851 -1.744 0.081205 .
mass:pedigree:age -0.3408 0.1845 -1.847 0.064722 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 498.10 on 391 degrees of freedom
Residual deviance: 330.71 on 380 degrees of freedom
AIC: 354.71
Number of Fisher Scoring iterations: 515.3.0.3 Búsqueda en ambas direcciones
Para hacer una búsqueda en ambas direcciones, usamos el argumento direction = "both":
lrm_both <- stepAIC(
lrm_null, direction = "both",
scope = list(lower = diabetes ~ 1, upper = diabetes ~ glucose * mass * pedigree * age)
)Start: AIC=500.1
diabetes ~ 1
Df Deviance AIC
+ glucose 1 386.67 390.67
+ age 1 450.67 454.67
+ mass 1 469.03 473.03
+ pedigree 1 481.37 485.37
<none> 498.10 500.10
Step: AIC=390.67
diabetes ~ glucose
Df Deviance AIC
+ age 1 370.69 376.69
+ mass 1 372.12 378.12
+ pedigree 1 376.34 382.34
<none> 386.67 390.67
- glucose 1 498.10 500.10
Step: AIC=376.69
diabetes ~ glucose + age
Df Deviance AIC
+ mass 1 354.37 362.37
+ pedigree 1 361.73 369.73
<none> 370.69 376.69
+ glucose:age 1 370.17 378.17
- age 1 386.67 390.67
- glucose 1 450.67 454.67
Step: AIC=362.37
diabetes ~ glucose + age + mass
Df Deviance AIC
+ pedigree 1 347.23 357.23
<none> 354.37 362.37
+ glucose:mass 1 352.76 362.76
+ mass:age 1 353.55 363.55
+ glucose:age 1 354.27 364.27
- mass 1 370.69 376.69
- age 1 372.12 378.12
- glucose 1 422.65 428.65
Step: AIC=357.23
diabetes ~ glucose + age + mass + pedigree
Df Deviance AIC
+ glucose:pedigree 1 340.80 352.80
+ glucose:mass 1 344.80 356.80
<none> 347.23 357.23
+ mass:pedigree 1 345.75 357.75
+ mass:age 1 346.50 358.50
+ pedigree:age 1 347.06 359.06
+ glucose:age 1 347.18 359.18
- pedigree 1 354.37 362.37
- mass 1 361.73 369.73
- age 1 363.70 371.70
- glucose 1 413.23 421.23
Step: AIC=352.8
diabetes ~ glucose + age + mass + pedigree + glucose:pedigree
Df Deviance AIC
<none> 340.80 352.80
+ glucose:mass 1 339.04 353.04
+ mass:age 1 339.99 353.99
+ mass:pedigree 1 340.49 354.49
+ glucose:age 1 340.60 354.60
+ pedigree:age 1 340.64 354.64
- glucose:pedigree 1 347.23 357.23
- age 1 356.68 366.68
- mass 1 356.73 366.73Veamos el resumen:
summary(lrm_both)
Call:
glm(formula = diabetes ~ glucose + age + mass + pedigree + glucose:pedigree,
family = binomial, data = dm_std)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.0249 0.1465 -6.996 2.63e-12 ***
glucose 1.1883 0.1608 7.390 1.47e-13 ***
age 0.5373 0.1389 3.869 0.000109 ***
mass 0.5533 0.1448 3.822 0.000132 ***
pedigree 0.4787 0.1399 3.423 0.000620 ***
glucose:pedigree -0.3224 0.1164 -2.769 0.005620 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 498.1 on 391 degrees of freedom
Residual deviance: 340.8 on 386 degrees of freedom
AIC: 352.8
Number of Fisher Scoring iterations: 515.4 Selección de modelos
Ahora veremos cómo evaluar un conjunto de modelos y los criterios para seleccionar un modelo final basados en medidas de performance, es decir, qué tan buena es la bondad de ajuste del modelo y qué tan bien predice.
Podemos usar la función compare_performance() del paquete performance para comparar múltiples modelos en base a diferentes indicadores de ajuste:
compare_performance(lrm_2, lrm_3, lrm_4, lrm_both)# Comparison of Model Performance Indices
Name | Model | AIC (weights) | AICc (weights) | BIC (weights) | Tjur's R2 | RMSE | Sigma | Log_loss | Score_log | Score_spherical | PCP
----------------------------------------------------------------------------------------------------------------------------------------------
lrm_2 | glm | 362.0 (0.008) | 362.5 (0.007) | 397.8 (<.001) | 0.364 | 0.376 | 1.000 | 0.439 | -74.015 | 0.009 | 0.718
lrm_3 | glm | 357.2 (0.087) | 357.4 (0.089) | 377.1 (0.411) | 0.359 | 0.377 | 1.000 | 0.443 | -73.555 | 0.008 | 0.716
lrm_4 | glm | 356.8 (0.108) | 357.0 (0.108) | 380.6 (0.070) | 0.361 | 0.376 | 1.000 | 0.440 | -72.291 | 0.010 | 0.717
lrm_both | glm | 352.8 (0.797) | 353.0 (0.796) | 376.6 (0.519) | 0.367 | 0.375 | 1.000 | 0.435 | -72.230 | 0.010 | 0.719Los indicadores más comunes son el AIC, BIC y el pseudo-R2 (Tjur’s R2 o R2 de Tjur). En este caso vemos que el modelo lrm_2 tiene un un mayor AIC y BIC. . El R2 de Tjur (también llamado coeficiente de discriminación) nos permite ver que tan bien los valores predichos del modelo discriminan las clases de respuesta. Mientras más se acerque a 1, mayor es la discriminación del modelo. Vemos que el modelo lrm_both tiene un mayor R2 de Tjur, seguido del modelo lrm_2.
Otra forma de medir el performance de los modelos de regresión logística es viendo qué tan bien clasifican las observaciones. Luego de hallar las probabilidades predichas, se toma la decisión de clasificar a una observación dependiendo de un valor de probabilidad de corte, que comúnmente es 0.5. Por ejemplo, en este caso, si una observación tiene una probabilidad predicha mayor a 0.5, entonces se le clasifica como positivo (tiene diabetes), de lo contrario se le clasifica como negativo (no tiene diabetes). Podemos evaluar que tan bien clasifica el modelo comparando la clase dada con las probabilidades predicha con la clase observada.
Para evaluar que tan bien clasifica el modelo a través de todos los posibles valores de corte, se utiliza el área bajo la curva ROC (Receiver Operating Characteristic), o AUC (Area Under ROC curve). A mayor el AUC, mayor el performance de clasificación del modelo.
Para calcular el AUC, primero tenemos que usar la función performance_roc() para obtener los valores de sensibilidad y especificidad por cada modelo y convertir el output en un data frame:
roc_values <- performance_roc(lrm_2, lrm_3, lrm_4, lrm_both) %>%
as_tibble()Luego, podemos usar la función area_under_curve() del paquete bayestestR para calcular el AUC por modelo:
library(bayestestR)
roc_values %>%
group_by(Model) %>%
summarise(auc = area_under_curve(Specificity, Sensitivity))# A tibble: 4 × 2
Model auc
<chr> <dbl>
1 lrm_2 0.862
2 lrm_3 0.860
3 lrm_4 0.860
4 lrm_both 0.862Vemos que el modelo lrm_both tiene mayor AUC, seguido de lrm_2.
También podemos graficar las curvas ROC usando plot():
plot(performance_roc(lrm_2, lrm_3, lrm_4, lrm_both))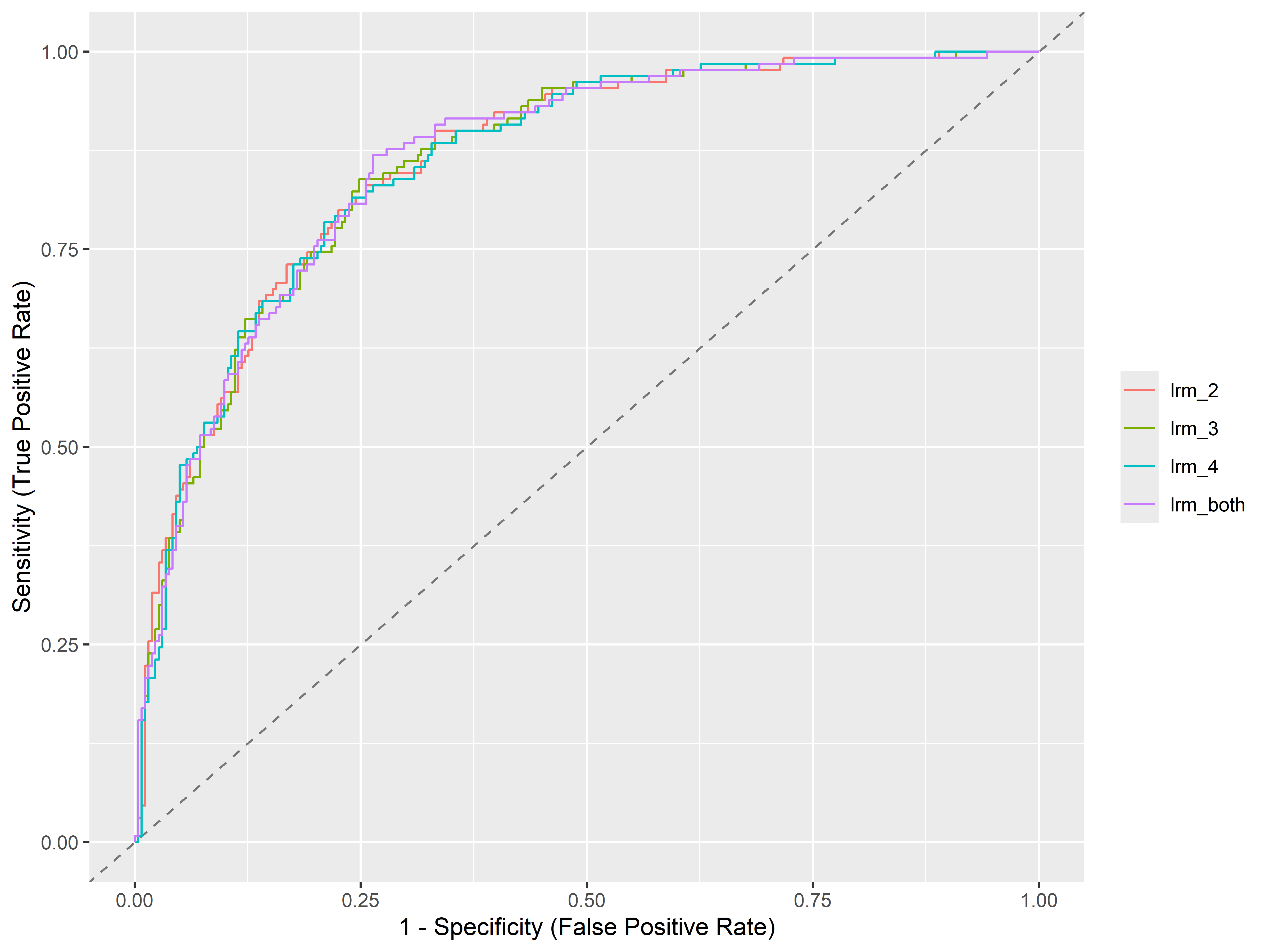
Para ver más métricas de evaluación de clasificación podemos usar las funciones del paquete yardstick. Para esto, debemos obtener las clases predichas y las clases observadas. Para mayor practicidad, podemos crear una función que extraiga las probabilidades predichas de un modelo con la función predict() y que luego transforme esas probabilidades en clases dependiendo si son mayores a 0.5 (pos) o no (neg). Por último, podemos extraer las clases observadas de la data del modelo y juntar las clases predichas y observadas en un data frame:
get_classes <- function(model) {
pred <- predict(model, type = "response")
pred_class <- ifelse(pred > 0.5, "pos", "neg")
truth_class <- model$model$diabetes
classes <- tibble(truth_class, pred_class)
classes <- classes %>%
mutate(
pred_class = factor(pred_class, levels = c("neg", "pos")),
truth_class = factor(truth_class, levels = c("neg", "pos"))
)
classes
}Por ejemplo, extraigamos las clases predichas y observadas de los modelos lrm_2 y lrm_both:
classes_lrm_2 <- get_classes(lrm_2)
classes_lrm_both <- get_classes(lrm_both)Ahora, pongamos estos data frames en una lista con el nombre de cada modelo:
models_classes_list <- list("lrm_2" = classes_lrm_2, "lrm_both" = classes_lrm_both)Por último, unamos los data frames usando la función bind_rows y agreguemos el argumento .id = "model" para que se cree una columna llamada model con los nombres de los modelos:
models_classes <- bind_rows(models_classes_list, .id = "model")Podemos definir múltiples métricas de evaluación usando la función metric_set(). Por ejemplo, incluyamos la exactitud (accuracy), el coeficiente Kappa (kap), la especificidad (spec) y la sensibilidad (sens):
Attaching package: 'yardstick'The following objects are masked from 'package:performance':
mae, rmseThe following object is masked from 'package:readr':
specmulti_metric <- metric_set(accuracy, kap, spec, sens)Ahora, para calcular estas métricas para ambos modelos, agrupamos por cada uno de ellos y pasamos las clases observadas (truth) y predichas (estimate) a multi_metric. Además, le decimos que el evento de interés es el segundo nivel (yes) de la variable de respuesta agregando el argumento event_level = "second":
models_classes %>%
group_by(model) %>%
multi_metric(truth = truth_class, estimate = pred_class, event_level = "second")# A tibble: 8 × 4
model .metric .estimator .estimate
<chr> <chr> <chr> <dbl>
1 lrm_2 accuracy binary 0.783
2 lrm_both accuracy binary 0.793
3 lrm_2 kap binary 0.484
4 lrm_both kap binary 0.518
5 lrm_2 spec binary 0.889
6 lrm_both spec binary 0.878
7 lrm_2 sens binary 0.569
8 lrm_both sens binary 0.623Para ver qué otras métricas se pueden utilizar, podemos revisar la referencia de funciones para métricas de clasificación del paquete yardstick.
La función diag_test() del paquete pubh también permite obtener un conjunto de métricas más sus intervalos de confianza para cada uno de los modelos. Por ejemplo, para el modelo lrm_2:
Outcome + Outcome - Total
Test + 74 29 103
Test - 56 233 289
Total 130 262 392
Point estimates and 95% CIs:
--------------------------------------------------------------
Apparent prevalence * 0.26 (0.22, 0.31)
True prevalence * 0.33 (0.29, 0.38)
Sensitivity * 0.57 (0.48, 0.66)
Specificity * 0.89 (0.84, 0.92)
Positive predictive value * 0.72 (0.62, 0.80)
Negative predictive value * 0.81 (0.76, 0.85)
Positive likelihood ratio 5.14 (3.54, 7.48)
Negative likelihood ratio 0.48 (0.40, 0.59)
False T+ proportion for true D- * 0.11 (0.08, 0.16)
False T- proportion for true D+ * 0.43 (0.34, 0.52)
False T+ proportion for T+ * 0.28 (0.20, 0.38)
False T- proportion for T- * 0.19 (0.15, 0.24)
Correctly classified proportion * 0.78 (0.74, 0.82)
--------------------------------------------------------------
* Exact CIsPor último, podemos usar la función confusionMatrix() del paquete caret. A esta función hay que pasarle la tabulación cruzada de las clases predichas y observadas. Por ejemplo, para el modelo lrm_2:
tbl_lrm_2 <- table(classes_lrm_2$pred_class,
classes_lrm_2$truth_class)
tbl_lrm_2
neg pos
neg 233 56
pos 29 74Ahora, pasamos esta tabla a la función confusionMatrix() e incluimos el argumento positive = "pos" para que tome la clase pos como el evento de interés:
library(caret)
confusionMatrix(tbl_lrm_2, positive = "pos")Confusion Matrix and Statistics
neg pos
neg 233 56
pos 29 74
Accuracy : 0.7832
95% CI : (0.739, 0.823)
No Information Rate : 0.6684
P-Value [Acc > NIR] : 3.836e-07
Kappa : 0.4839
Mcnemar's Test P-Value : 0.004801
Sensitivity : 0.5692
Specificity : 0.8893
Pos Pred Value : 0.7184
Neg Pred Value : 0.8062
Prevalence : 0.3316
Detection Rate : 0.1888
Detection Prevalence : 0.2628
Balanced Accuracy : 0.7293
'Positive' Class : pos
Podemos utilizar la función tidy() del paquete broom para generar un tibble con los resultados:
library(broom)
conf_mat_lrm_2 <- confusionMatrix(tbl_lrm_2, positive = "pos")
tidy(conf_mat_lrm_2)# A tibble: 14 × 6
term class estimate conf.low conf.high p.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl>
1 accuracy <NA> 0.783 0.739 0.823 0.000000384
2 kappa <NA> 0.484 NA NA NA
3 mcnemar <NA> NA NA NA 0.00480
4 sensitivity pos 0.569 NA NA NA
5 specificity pos 0.889 NA NA NA
6 pos_pred_value pos 0.718 NA NA NA
7 neg_pred_value pos 0.806 NA NA NA
8 precision pos 0.718 NA NA NA
9 recall pos 0.569 NA NA NA
10 f1 pos 0.635 NA NA NA
11 prevalence pos 0.332 NA NA NA
12 detection_rate pos 0.189 NA NA NA
13 detection_prevalence pos 0.263 NA NA NA
14 balanced_accuracy pos 0.729 NA NA NA