10  Contraste de variables continuas

Autores/as

Carrasco Escobar, Gabriel

Villa Almeyda, Diego

10.1 General

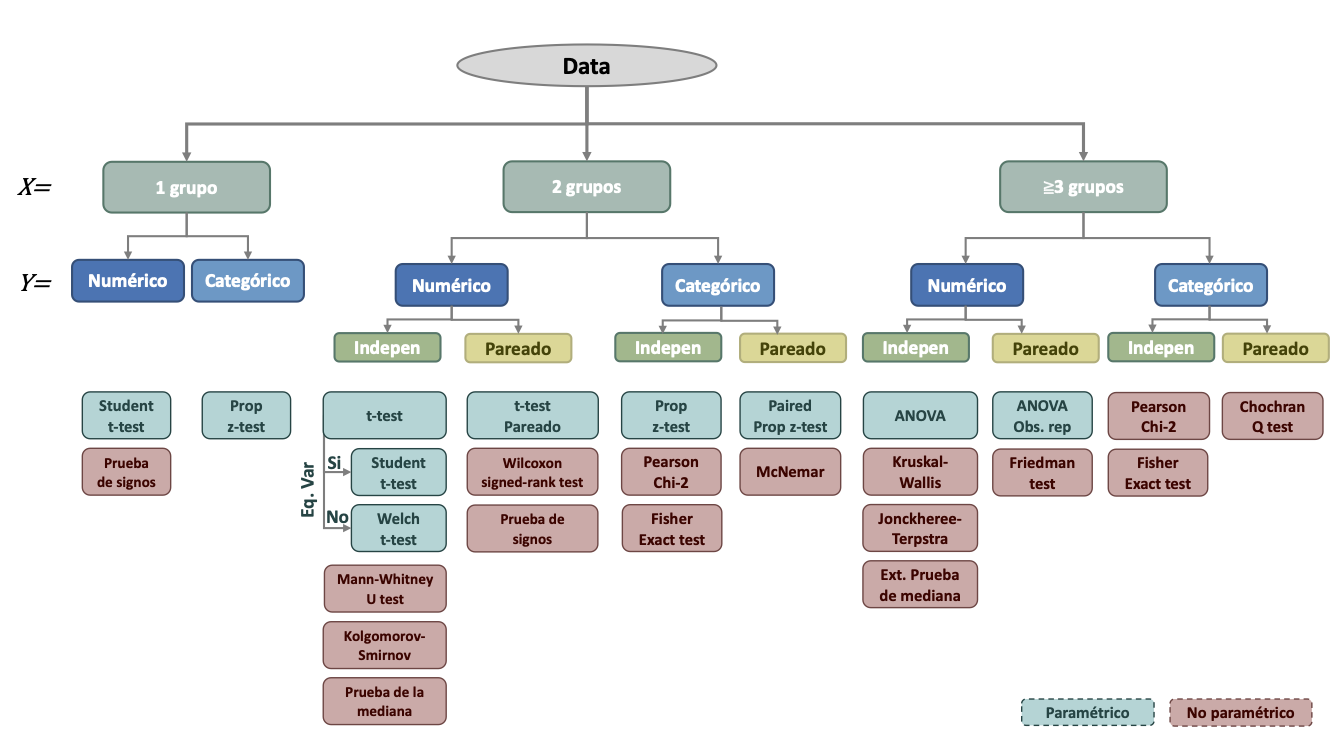
En esta sección exploraremos múltiples funciones para hacer inferencia estadística. Estas pruebas se pueden dividir de acuerdo al número de grupos a comparar ( x ), al tipo (numérica o continua) de variable dependiente ( y ) y si las observaciones entre ambos grupos son independientes o realacionadas (pareadas). Usaremos este esquema general para organizar esta sección. Sin embargo, no representa una lista exhaustiva de todas las pruebas estadísticas disponibles en R y tampoco se abordarán todas las pruebas mencionadas.

10.2 Paquetes y data

Los paquetes y conjuntos de datos a ser utilizados en esta sección son:

Efectos de la exposición al plomo en la función neurológica y psicológica de los niños

Landrigan et al. (1975) estudiaron los efectos de la exposición a plomo en el bienestar psicológico y neurológico en niños. Se midió el nivel de plomo en la sangre de niños que vivían cerca a lugares donde se realizaba fundición de plomo en El Paso, Texas. 124 niños entraron al estudio, los cuales fueron separados en 2 grupos según su nivel de plomo en la sangre. En el primer grupo se incluyó a niños con niveles de plomo en la sangre \(<40 \mu\)g/100ml (78 casos), mientras que en el segundo a niños con niveles de plomo en la sangre \(\geq40 \mu\)g/100ml (76 casos). Diversos indicadores psicológicos y neurológicos se midieron en los niños, siendo los dos más importantes el número de taps con los dedos y muñeca en la mano dominante (Finger-Wrist tapping test) y el puntaje IQ de escala completa de Wechsler.

El data set de este estudio fue recuperado de Rosner (2015) y se encuentra en el archivo lead.csv de la carpeta de datos. Algunos nombres de variables se modificaron para mayor claridad en la lectura.

lead <- read_csv("data/lead.csv")

10.3 Pruebas de una muestra

La variable que contiene la última medición de niveles de plomo en la sangre es ld73. Landrigan et al. (1975) sostienen que en investigaciones pasadas se ha encontrado una prevalencia de niveles de plomo en la sangre en el rango de 40 a 80\(\mu\)g/100ml en la población de estudio. Usaremos este dato para corroborar si la muestra nos evidencia que el nivel medio del nivel de plomo en la sangre de los niños es mayor a 40\(\mu\)g/100ml.

10.3.1 Prueba t

Supuestos:

Caso 1:

  • Distribución de la población es aproximadamente normal.
  • Varianza poblacional desconocida.

Caso 2:

  • Distribución de la población no es aproximadamente normal o se desconoce.
  • Tamaño de muestra grande.

Para realizar la prueba t, es necesario verificar que la distribución de la muestra sea aproximadamente normal. En la práctica, rara vez se da el caso de que la distribución es exactamente normal, por eso hablamos en términos de aproximación. Se recomienda utilizar métodos gráficos para evaluar la distribución. En principio, podemos usar un histograma o un Q-Q plot.

Veamos primero un resumen descriptivo de esta variable con summary().

summary(lead$ld73)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  15.00   24.00   30.50   31.71   37.00   58.00

La media muestral es de 31.71\(\mu\)g/100ml, un poco alejado del valor de prueba de 40\(\mu\)g/100ml, pero aún no sabemos si estadísticamente esta diferencia es significativa. Vemos que la mediana es un poco menor que la media, por lo que podríamos esperar que la distribución esté algo sesgada (hacia la derecha). Analicemos ahora el histograma.

lead %>% 
  ggplot(aes(ld73)) +
  geom_histogram(bins = 10)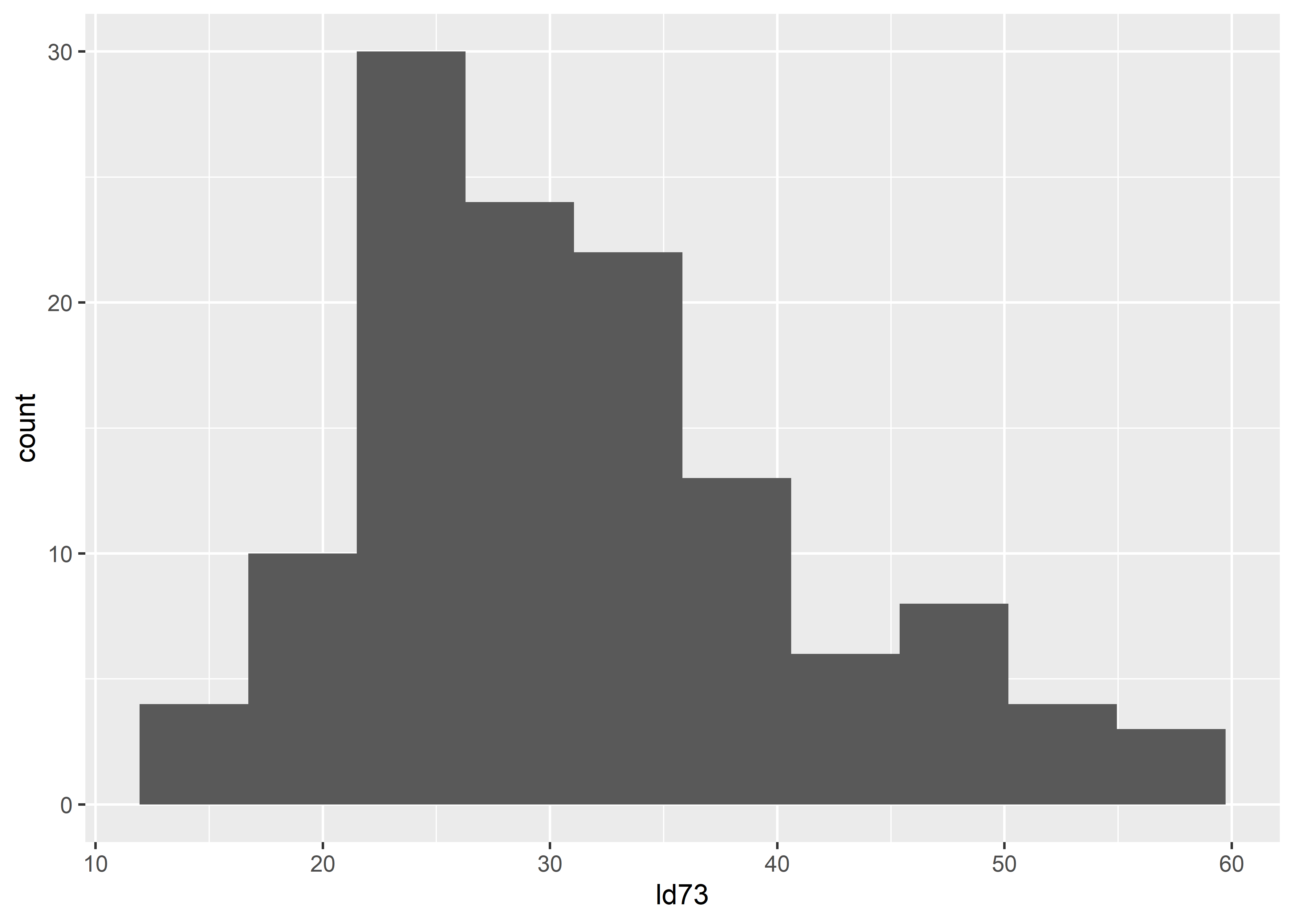

Vemos que la distribución de la muestra efectivamente está un poco sesgada a la derecha, pero pareciera no están tan lejos de tener aproximadamente una distribución normal. Si añadimos el valor de prueba de 40\(\mu\)g/100ml podremos ver gráficamente la diferencia entre el promedio muestra y el valor de prueba.

lead %>% 
  ggplot(aes(ld73)) +
  geom_histogram(bins = 10) +
  geom_vline(aes(xintercept = mean(ld73), color = "Promedio"), 
             size = 1) +
  geom_vline(aes(xintercept = 40, color = "Valor de prueba"), size = 1) +
  guides(color = guide_legend( title = "Referencias"))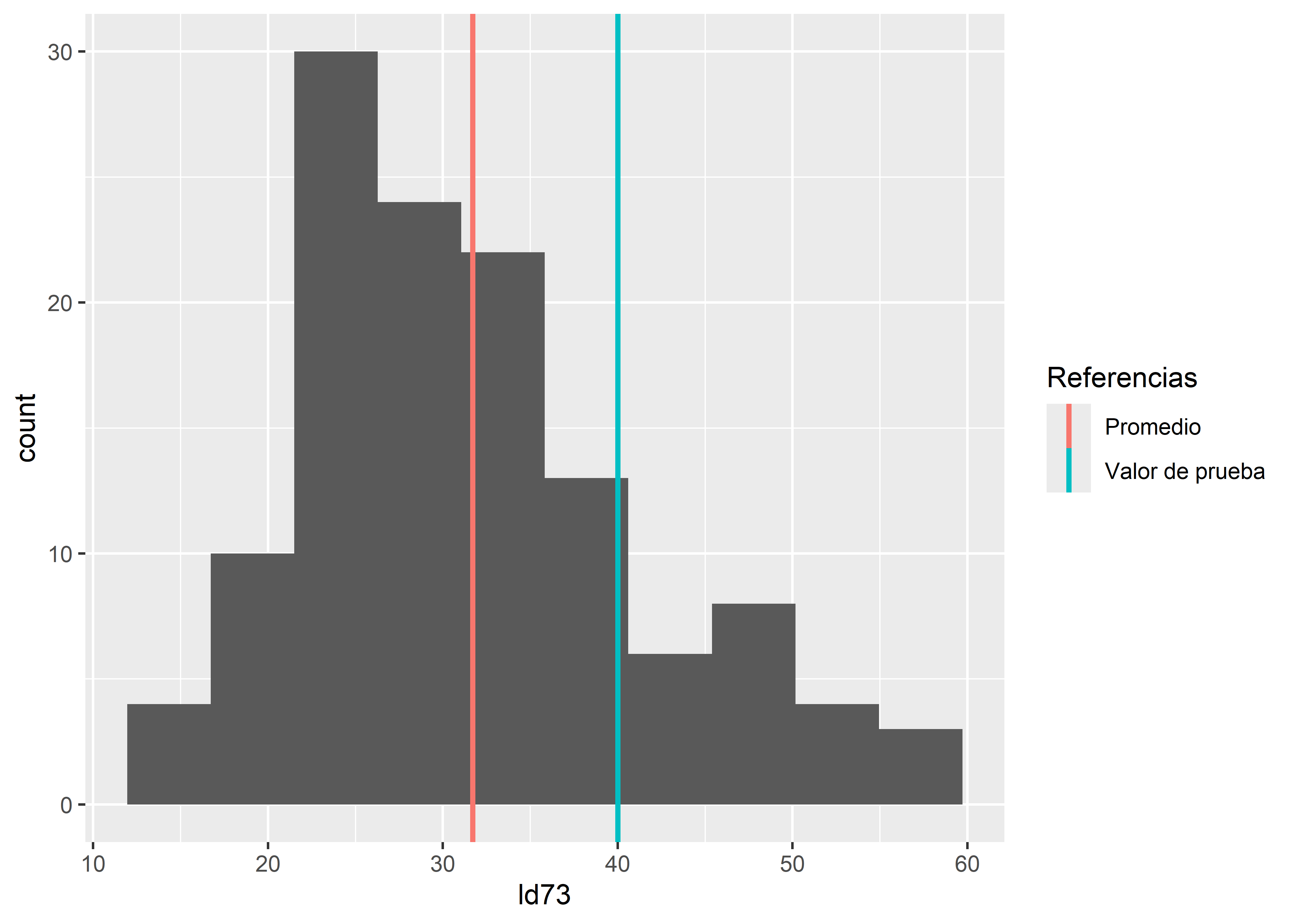

Una mejor forma de corroborar que la distribución de la muestra es aproximadamente normal, es utilizando el Q-Q plot. En un Q-Q plot se comparan los cuantiles muestrales de la data con los cuantiles teóricos de la distribución normal.

lead %>% 
  ggplot(aes(sample = ld73)) +
  stat_qq() +
  stat_qq_line()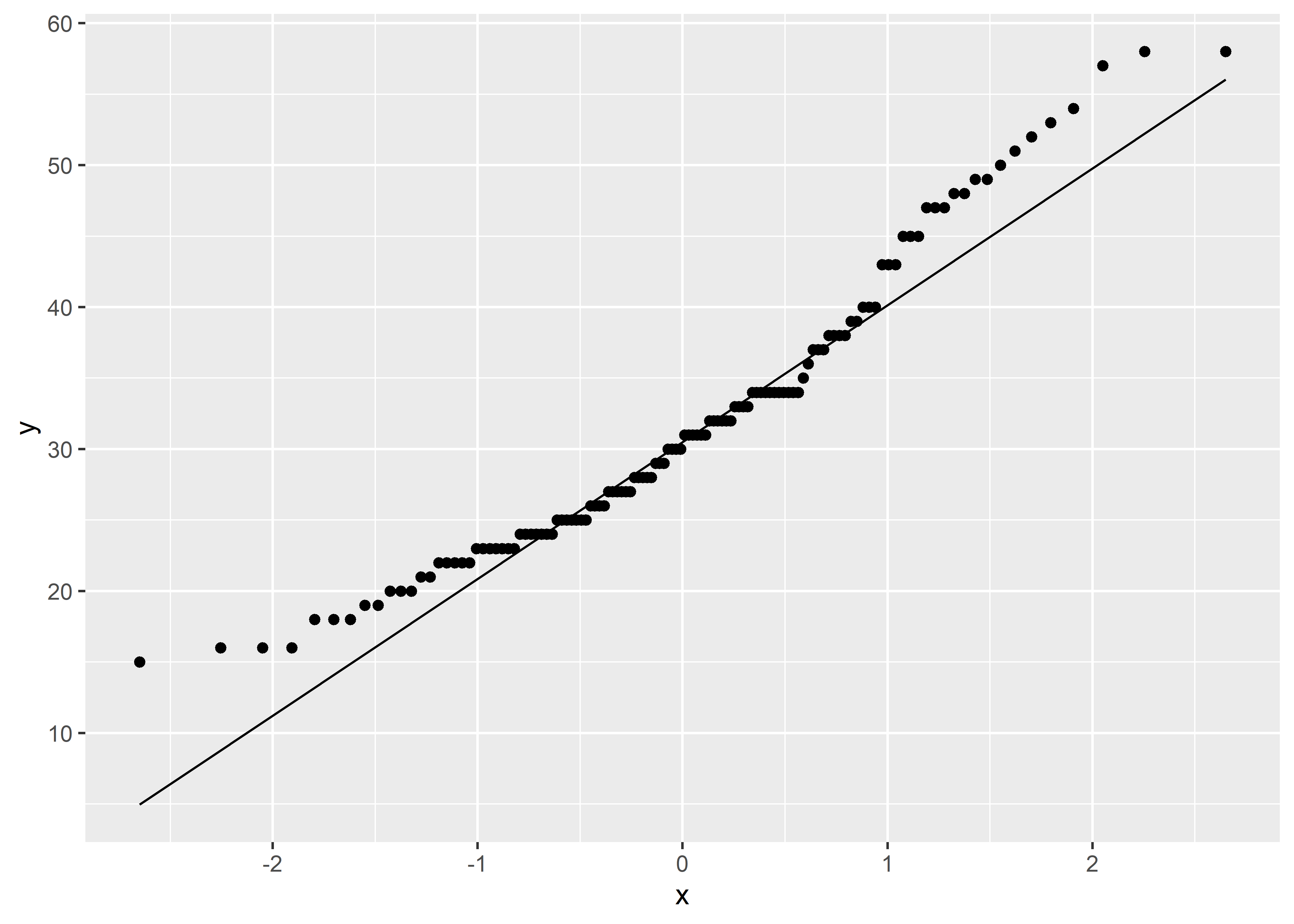

La línea nos da una referencia de qué tanto son equivalentes los cuantiles muestrales y los cuantiles teóricos. En este caso podemos ver que existe una disparidad entre los cuantiles en las colas de la distribución. Esto evidencia mejor que la data no sigue exactamente una distribución normal. Pero, de nuevo, en la práctica esto casi nunca se cumple y tenemos que evaluar este supuesto en base a aproximaciones. En este sentido, pareciera plausible asumir una distribución normal ya que los gráficos nos muestran que si bien existe una diferencia entre la distribución real y la teórica, esta no es muy excesiva como para descartar este supuesto. Además, algunos resultados teóricos indican que la prueba t es relativamente robusta al supuesto de normalidad, especialmente para muestras grandes. Robustness

Puede ser tentador transformar los datos de la muestra para que la distribución se aproxime mejor a la distribución normal, por ejemplo utilizar una transformación logarítmica. Sin embargo, esto no siempre es recomendable, ya que, entre otras razones, las inferencias que se hagan sobre la data transformada no necesariamente van a ser relevantes para la data original o no-transformada. Transformations

Habiendo ya discutido sobre la distribución de la muestra, procederemos a realizar la prueba t. En R, el paquete base stats provee de casi todas las pruebas de significancia estadística más usadas en la práctica. La función t.test() de este paquete permite realizar la prueba t y nos arroja los resultados correspondientes.

t.test(ld73 ~ 1, alternative = "greater", mu = 40, data = lead)

    One Sample t-test

data:  ld73
t = -9.2956, df = 123, p-value = 1
alternative hypothesis: true mean is greater than 40
95 percent confidence interval:
 30.23157      Inf
sample estimates:
mean of x 
 31.70968

Según la prueba, no hay alguna evidencia en contra de la hipótesis nula de que la media es menor o igual 40\(\mu\)g/100ml. En otras palabras, la media del nivel de plomo en la sangre en los niños no es significativamente mayor a 40\(\mu\)g/100ml.

Un paquete que ofrece una implementación tidy de la prueba t es rstatix mediante la función t_test().

lead %>%
  t_test(formula = ld73 ~ 1, alternative = "greater", mu = 40)
# A tibble: 1 × 7
  .y.   group1 group2         n statistic    df     p
* <chr> <chr>  <chr>      <int>     <dbl> <dbl> <dbl>
1 ld73  1      null model   124     -9.30   123     1

Para ver a mayor detalle los resultados de la inferencia, incluyendo el intervalo de confianza, debemos agregar el argumento detailed = TRUE.

lead %>%
  t_test(formula = ld73 ~ 1, alternative = "greater", mu = 40, 
         detailed = TRUE)
# A tibble: 1 × 12
  estimate .y.   group1 group2        n statistic     p    df conf.low conf.high
*    <dbl> <chr> <chr>  <chr>     <int>     <dbl> <dbl> <dbl>    <dbl>     <dbl>
1     31.7 ld73  1      null mod…   124     -9.30     1   123     30.2       Inf
# ℹ 2 more variables: method <chr>, alternative <chr>

10.3.2 Prueba de signos

Supuestos:

  • Distribución de la población aproximadamente no normal.
  • Tamaño de muestra es pequeña.

La prueba de signos es una alternativa no-paramétrica de la prueba t. En otras palabras, para realizar la prueba de signos, no es necesario asumir alguna distribución paramétrica para la muestra. Recordemos que en el caso de la prueba t era necesario demostrar que la muestra tenía una distribución aproximadamente normal.

Las pruebas no-paramétricas, generalmente, trabajan con la distribución de alguna transformación de los datos de la muestra, de manera que no tengamos que asumir alguna distribución para la muestra original. Esto hace que se usen otros parámetros para evaluar las hipótesis. En el caso de la prueba de signos, y de otras pruebas que se generan de esta, se utiliza la mediana. La media, que se utilizaba en la prueba t, como la mediana, son parámetros de locación de una distribución. Por esta razón, en general a este tipo de pruebas se les llama pruebas de locación.

Una primera implementación de la prueba de signos se encuentra en el paquete BSDA. La función se llama SIGN.test(). En este prueba, se tiene que especificar como valor de prueba a la mediana en el argumento md.

SIGN.test(lead$ld73, md = 40, alternative = "greater")

    One-sample Sign-Test

data:  lead$ld73
s = 21, p-value = 1
alternative hypothesis: true median is greater than 40
95 percent confidence interval:
  28 Inf
sample estimates:
median of x 
       30.5 

Achieved and Interpolated Confidence Intervals: 

                  Conf.Level L.E.pt U.E.pt
Lower Achieved CI     0.9367     28    Inf
Interpolated CI       0.9500     28    Inf
Upper Achieved CI     0.9562     28    Inf

El paquete DescTools también ofrece una implementación de la prueba de signos mediante la función SignTest().

SignTest(lead$ld73, mu = 40, alternative = "greater")

    One-sample Sign-Test

data:  lead$ld73
S = 21, number of differences = 121, p-value = 1
alternative hypothesis: true median is greater than 40
95.6 percent confidence interval:
  28 Inf
sample estimates:
median of the differences 
                     30.5

Una implementación más tidy se encuentra en el paquete rstatix. Similar a la función t_test(), la función sign_test() devuelve los resultados en un tibble.

lead %>%
  sign_test(formula = ld73 ~ 1, alternative = "greater", mu = 40, 
            detailed = TRUE)
# A tibble: 1 × 12
  estimate .y.   group1 group2        n statistic     p    df conf.low conf.high
*    <dbl> <chr> <chr>  <chr>     <int>     <dbl> <dbl> <dbl>    <dbl>     <dbl>
1     30.5 ld73  1      null mod…   124        21     1   121       28       Inf
# ℹ 2 more variables: method <chr>, alternative <chr>

10.4 Pruebas de dos muestras independientes

Regresando al caso de estudio de niveles de plomo en sangre de niños, recordemos que el objetivo era evaluar si en el grupo más expuesto al plomo los indicadores psicológicos y neurológicos eran peores que el grupo menos expuesto. En la data, la variable de agrupación es la variable Group. En esta sección analizaremos la diferencia entre las puntuaciones de la prueba psicológica entre los dos grupos. En este caso, se usó el puntaje IQ de escala completa de Wechsler, cuyas mediciones se encuentran en la variable iqf.

Veamos un box-plot para analizar gráficamente la diferencia entre los puntajes de IQ entre los grupos. Primero, convertiremos la variable Group en un factor para un mejor manejo.

lead <- lead %>%
  mutate(group_fct = factor(Group))

Ahora, construyamos el box-plot.

lead %>% 
  ggplot(aes(group_fct, iqf)) +
  geom_boxplot()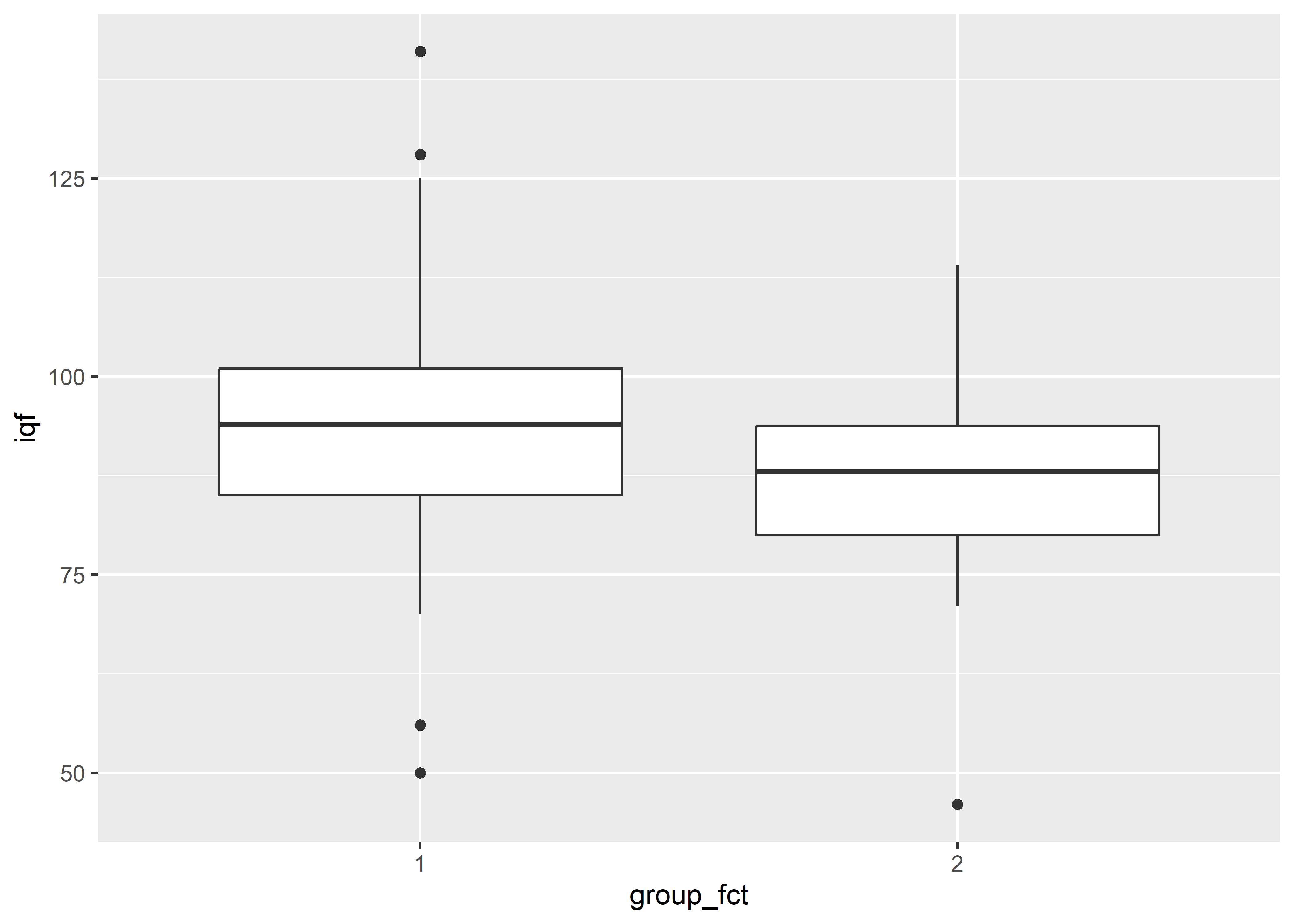

Observamos que los puntajes de IQ del segundo grupo con mayores niveles de plomo en la sangre parecen ser menores que los del primer grupo. Para enriquecer este gráfico, se disminuirá el ancho de las cajas y se agregará una capa de gráfico de violín.

lead %>% 
  ggplot(aes(group_fct, iqf)) +
  geom_violin() +
  geom_boxplot(width = 0.2)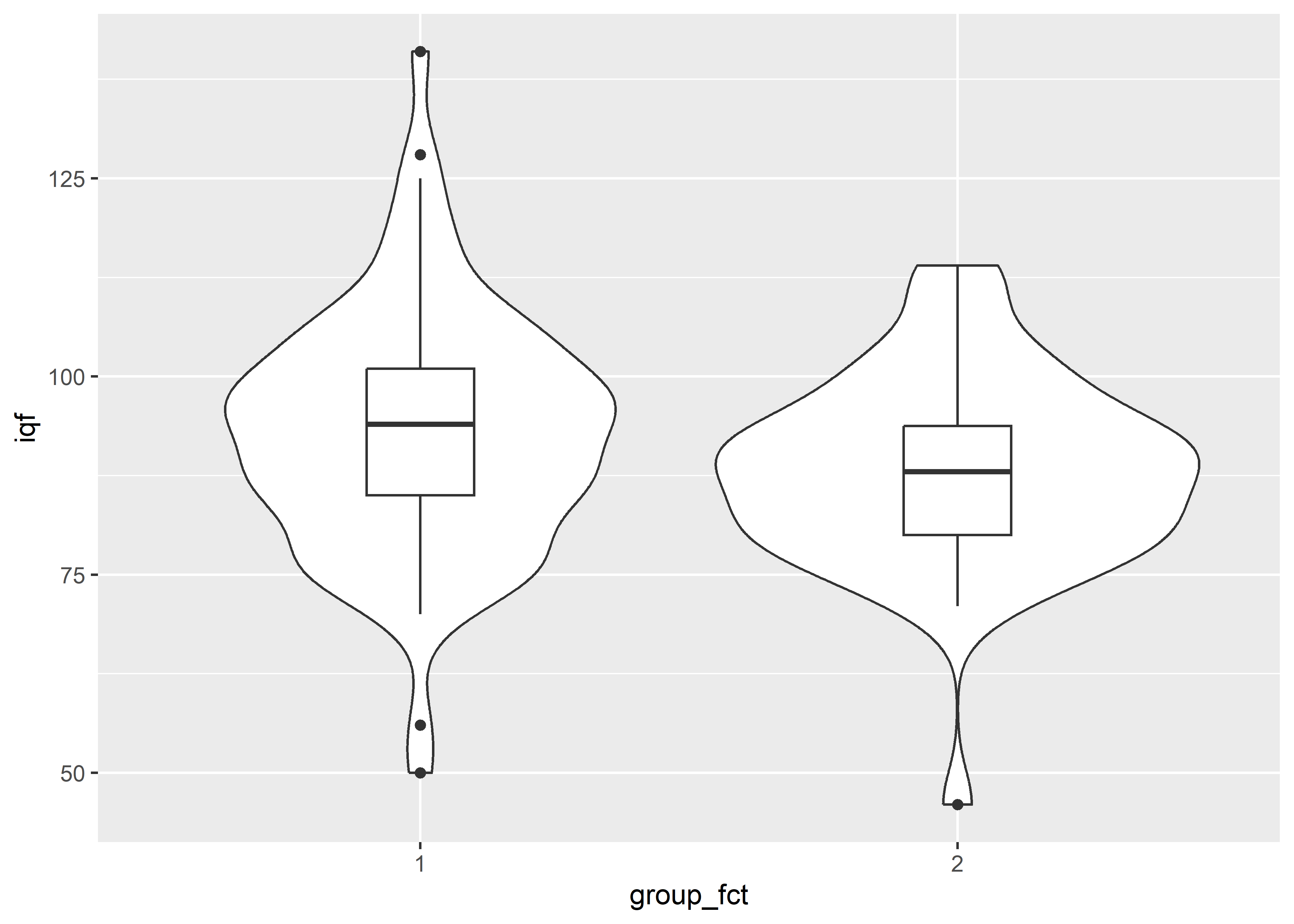

Los gráficos de violín muestran la forma de la densidad de la distribución de las variables. Los picos representan regiones de alta densidad, es decir, donde se concentra una gran cantidad de observaciones. Los gráficos de violín están relacionados con los histogramas. Estos últimos trabajan con la frecuencia de observaciones dentro de cada intervalo, mientras que los gráficos de violín utilizan una técnica llamada kernel density estimation para mostrar estas frecuencias de manera relativa y de forma continua.

Vemos en el gráfico anterior que la distribución del IQ en el segundo grupo tiene un menor rango y un pico más alto (mayor densidad en la zona central) y, por tanto, mayor curtosis que en el primer grupo. Además, no parece haber un problema de asimetría en alguno de los grupos.

10.4.1 Prueba t

Prueba t de Student

Supuestos:

  • Variables independientes.
  • Distribución de la muestra aproximadamente normal.
  • Varianzas poblacionales desconocidas.
  • Varianzas de las muestras iguales, se asume si n < 50 en cada grupo.

Prueba t de Welch o de varianzas diferentes

Supuestos:

  • Variables independientes.
  • Distribución de la muestra aproximadamente normal.
  • Varianzas poblacionales desconocidas.
  • Varianzas de las muestras diferentes, se asume si n > 50 en cada grupo.

Para la prueba t para dos muestras independientes tenemos que evaluar que la distribución de las muestras sea aproximadamente normal.

lead %>% 
  ggplot(aes(sample = ld73)) +
  facet_wrap(vars(group_fct)) +
  stat_qq() +
  stat_qq_line()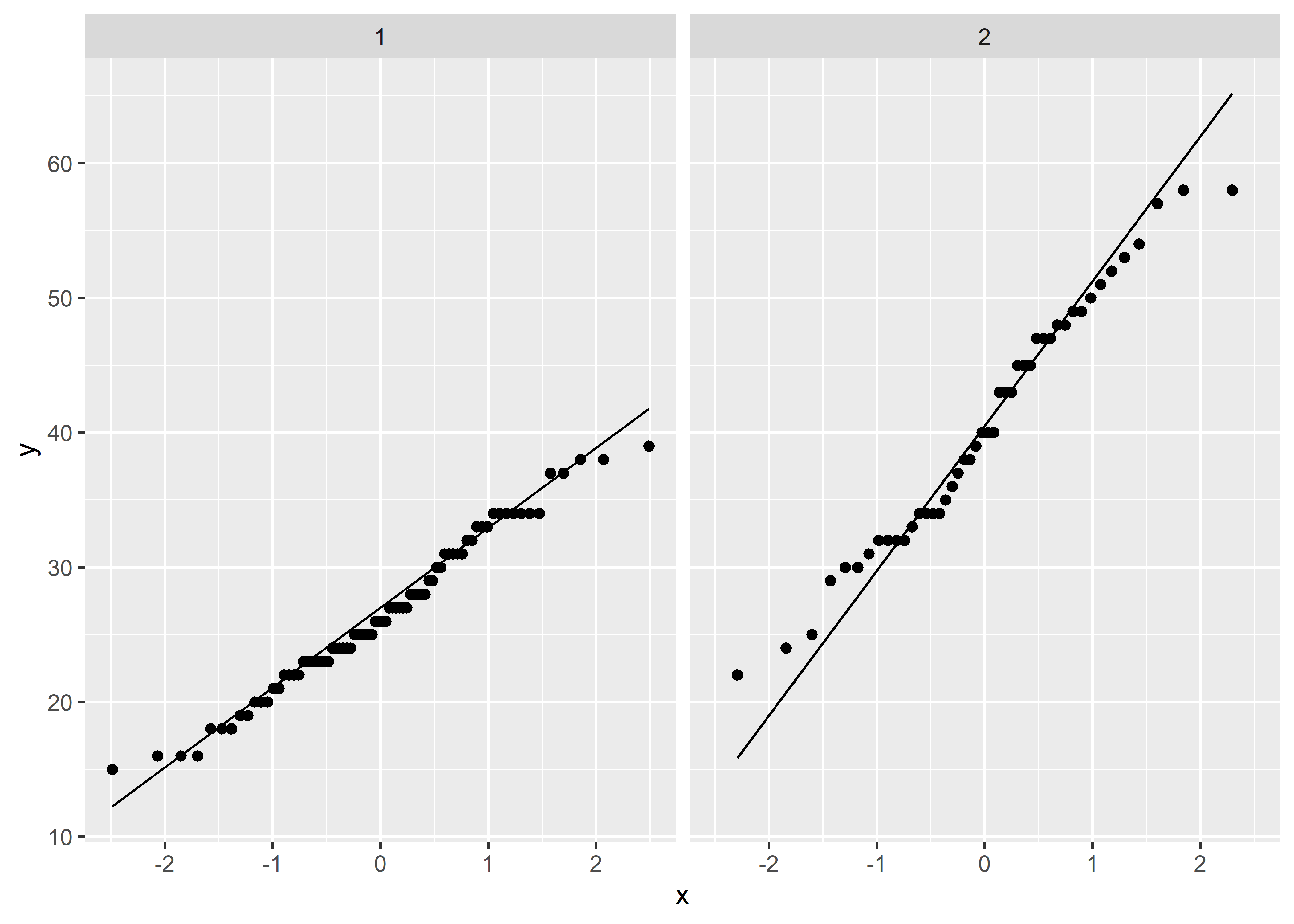

Por los Q-Q plots, pareciera que las muestras de cada grupo no están lejos de tener una distribución aproximadamente normal.

Existen dos versiones de la prueba t para dos muestras independientes. Se diferencian en que una asume que las varianzas de las muestras son iguales (prueba t de Student) y la otra no (prueba t de Welch). Para determinar si las varianzas son iguales utilizamos var.test().

var.test(iqf ~ group_fct, data = lead)

    F test to compare two variances

data:  iqf by group_fct
F = 1.5802, num df = 77, denom df = 45, p-value = 0.09817
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.9172764 2.6245411
sample estimates:
ratio of variances 
          1.580234

Al no rechazar la hipótesis nula, tenemos poca evidencia de que las varianzas de ambos grupos son diferentes.

La prueba t para dos muestras se realiza con la función base t.test() añadiendo la variable de grupos en la formula. En este caso, tenemos que especificar que es una prueba con varianzas iguales agregando el argumento var.equal = TRUE

t.test(iqf ~ group_fct, alternative = "two.sided", mu = 0, var.equal = TRUE, data = lead)

    Two Sample t-test

data:  iqf by group_fct
t = 1.8334, df = 122, p-value = 0.06918
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
 -0.3877812 10.1135337
sample estimates:
mean in group 1 mean in group 2 
       92.88462        88.02174

Por defecto, t.test() asume que las varianzas no son iguales y se estiman las varianzas separadamente para cada grupos. A esta versión se le llama la prueba t de Welch.

t.test(iqf ~ group_fct, alternative = "two.sided", mu = 0, data = lead)

    Welch Two Sample t-test

data:  iqf by group_fct
t = 1.9439, df = 111.41, p-value = 0.05442
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
 -0.09391511  9.81966762
sample estimates:
mean in group 1 mean in group 2 
       92.88462        88.02174

De los resultados, podemos ver que si bien la media muestral del grupo con menores niveles de concentración de plomo es mayor que la del grupo con menor concentración, no hay una fuerte evidencia para asegurar que la diferencia sea significativa.

Veamos ahora cómo realizar esta prueba con el paquete rstatix.

# Varianzas iguales
lead %>% 
  t_test(iqf ~ group_fct, alternative = "two.sided", mu = 0, 
                detailed = TRUE, var.equal = TRUE)
# A tibble: 1 × 15
  estimate estimate1 estimate2 .y.   group1 group2    n1    n2 statistic      p
*    <dbl>     <dbl>     <dbl> <chr> <chr>  <chr>  <int> <int>     <dbl>  <dbl>
1     4.86      92.9      88.0 iqf   1      2         78    46      1.83 0.0692
# ℹ 5 more variables: df <dbl>, conf.low <dbl>, conf.high <dbl>, method <chr>,
#   alternative <chr>
# Varianzas diferentes
lead %>% 
  t_test(iqf ~ group_fct, alternative = "two.sided", mu = 0, 
                detailed = TRUE)
# A tibble: 1 × 15
  estimate estimate1 estimate2 .y.   group1 group2    n1    n2 statistic      p
*    <dbl>     <dbl>     <dbl> <chr> <chr>  <chr>  <int> <int>     <dbl>  <dbl>
1     4.86      92.9      88.0 iqf   1      2         78    46      1.94 0.0544
# ℹ 5 more variables: df <dbl>, conf.low <dbl>, conf.high <dbl>, method <chr>,
#   alternative <chr>

10.4.2 Prueba U de Mann-Whitney

Supuestos:

  • Variables independientes.
  • Distribución no normal.
  • Tamaño de muestra pequeña.

El equivalente no-paramétrico para la prueba t para muestras independientes es la prueba U de Mann-Whitney. A esta prueba también se le conoce como la prueba de suma de rangos de Wilcoxon. En R, la función base es wilcox.test().

wilcox.test(iqf ~ group_fct, alternative = "two.sided", mu = 0, data = lead)

    Wilcoxon rank sum test with continuity correction

data:  iqf by group_fct
W = 2147.5, p-value = 0.0677
alternative hypothesis: true location shift is not equal to 0

Al igual que en la prueba t, no hay suficiente evidencia para concluir que hay diferencia entre los dos grupos.

Una versión tidy se encuentra en el paquete rstatix mediante la función wilcox_test().

lead %>%
  wilcox_test(formula = iqf ~ group_fct, alternative = "two.sided", 
              mu = 0, detailed = TRUE)
# A tibble: 1 × 12
  estimate .y.   group1 group2    n1    n2 statistic      p   conf.low conf.high
*    <dbl> <chr> <chr>  <chr>  <int> <int>     <dbl>  <dbl>      <dbl>     <dbl>
1     5.00 iqf   1      2         78    46     2148. 0.0677 -0.0000294      9.00
# ℹ 2 more variables: method <chr>, alternative <chr>

10.5 Pruebas de dos muestras pareadas

En esta sección utilizaremos el caso de estudio de los efectos del consumo de tabaco en la densidad ósea en gemelas. Hopper, J.L. y Seeman (1994) realizaron un estudio en gemelas sobre la relación entre densidad ósea y consumo de cigarros. Cuarenta y un pares de gemelas de mediana edad que no tenían el mismo hábito de consumo de tabaco fueron invitadas a un hospital en Victoria, Australia, para una medición de densidad ósea. Además, se obtuvo detalles acerca del uso de tabaco, consumo de alcohol, café y té, ingesta de calcio, historia menopáusica, reproductiva y de fracturas, uso de anticonceptivos orales o terapia de reemplazo de estrógenos, y se evaluo su actividad física.

Las muestras, en este caso, son pareadas porque las gemelas tienen características (genéticas, sociales, ambientales, etc.) similares, y la única diferencia se está midiendo a nivel de consumo de tabaco. Este tipo de pruebas también suelen ser utilizadas cuando se mide múltiples veces a un individuo. En este caso, las mediciones están relacionadas por pertenecer al mismo participante.

Leamos la data que se encuentra en el archivo boneden.csv.

boneden <- read_csv("data/boneden.csv")

Analizaremos la densidad ósea de la espina lumbar que se encuentra en la variable ls1 para gemela que no fuma y en la variable ls2 para la que fuma.

10.5.1 Prueba t

Supuestos:

  • Variables pareadas.
  • La distribución de las diferencias entre las observaciones es aproximadamente normal o tamaño de muestra es grande.
  • Varianzas poblacionales desconocidas.

Como en los casos anteriores, la prueba t asume una distribución aproximadamente normal para la muestra. En este caso, este supuesto se aplica a la diferencia entre las observaciones de la densidad ósea. Construyamos un Q-Q plot para evaluar este supuesto.

boneden %>% 
  ggplot(aes(sample = ls2 - ls1)) +
  stat_qq() +
  stat_qq_line()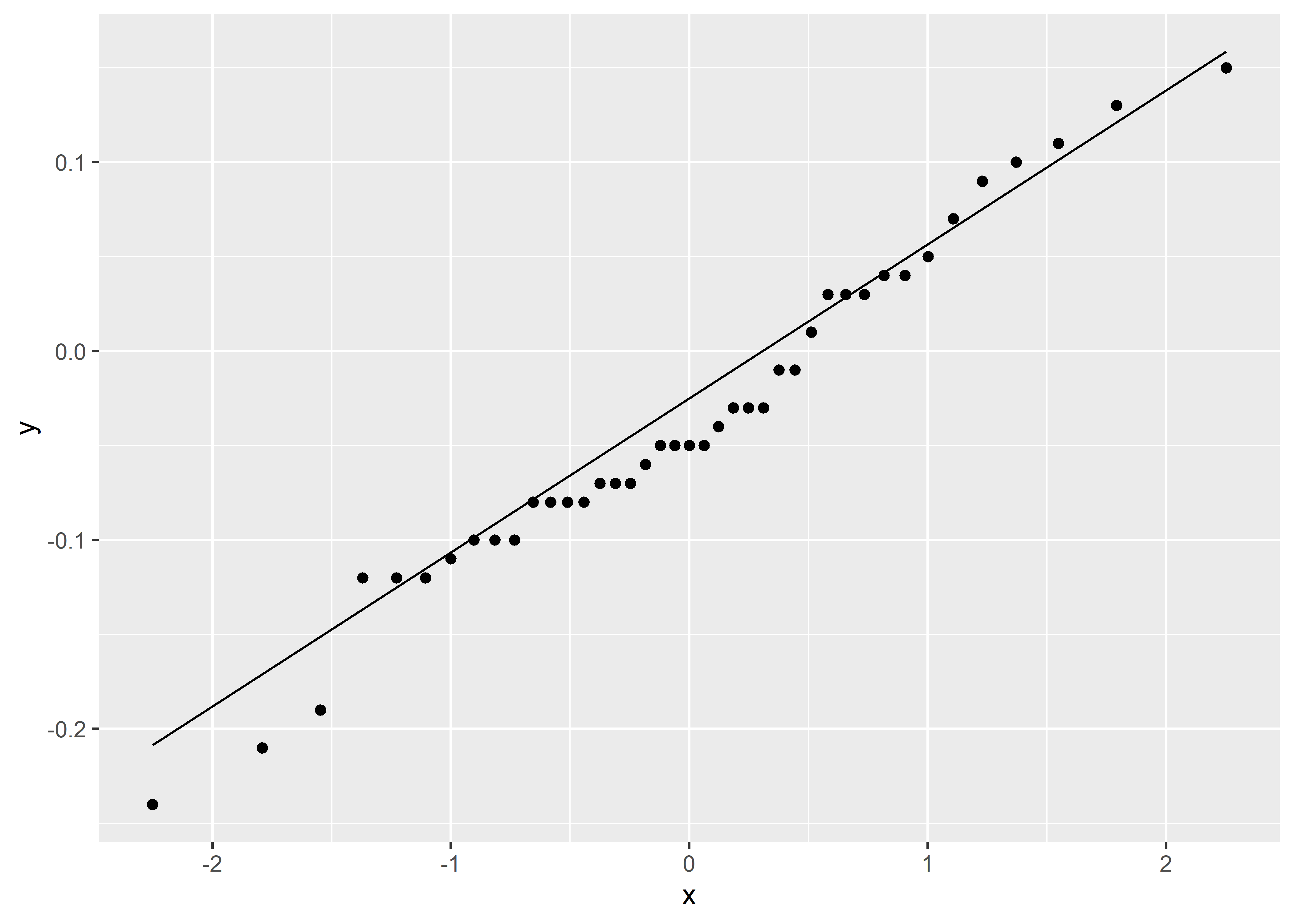

Vemos del gráfico que el supuesto de normalidad es bastante plausible para esta muestra.

Para un mejor manejo, necesitamos poner la data en formato largo (long) y cambiar el formato de la variable grupo a un factor.

boneden_long <- boneden %>%
  pivot_longer(cols = c("ls1", "ls2"), names_to = "group", values_to = "ls") %>%
  mutate(group = factor(group))

Para realizar la prueba t pareada, solo necesitamos agregar el argumento paired = TRUE en las funciones de prueba t que hemos visto antes. Por ejemplo, en la función base:

t.test(
  ls ~ group, alternative = "two.sided", mu = 0, paired = TRUE, 
  data = boneden_long
)

    Paired t-test

data:  ls by group
t = 2.6003, df = 40, p-value = 0.01299
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 0.007986336 0.063720981
sample estimates:
mean difference 
     0.03585366

Los resultados de la prueba nos indican que la muestra proporciona evidencia que hay una diferencia significativa entre la densidad ósea en la espina lumbar de las gemelas que bastante tabaco y las que no.

La función t_test() del paquete rstatix permite también realizar pruebas pareadas utilizando el argumento paired = TRUE.

boneden_long %>% 
  t_test(ls ~ group, paired = TRUE, alternative = "two.sided", mu = 0,
         detailed = TRUE)
# A tibble: 1 × 13
  estimate .y.   group1 group2    n1    n2 statistic     p    df conf.low
*    <dbl> <chr> <chr>  <chr>  <int> <int>     <dbl> <dbl> <dbl>    <dbl>
1   0.0359 ls    ls1    ls2       41    41      2.60 0.013    40  0.00799
# ℹ 3 more variables: conf.high <dbl>, method <chr>, alternative <chr>

10.5.2 Prueba de rango con signo de Wilcoxon

Supuestos:

  • Variables pareadas.
  • La distribución de las diferencias entre las observaciones no es normal o el tamaño de muestra es pequeño.

Esta prueba es el equivalente no-paramétrico para la prueba t pareada. Para usarla, en la función base wilcox.test() necesitamos agregar el parámetro paired = TRUE.

wilcox.test(ls ~ group, alternative = "two.sided", mu = 0, paired = TRUE, 
            data = boneden_long)

    Wilcoxon signed rank test with continuity correction

data:  ls by group
V = 617.5, p-value = 0.0156
alternative hypothesis: true location shift is not equal to 0

Como vemos, hay un problema con algunos datos que se encuentran empatados. Esta prueba utiliza rangos para calcular la estadística de prueba, y cuando se presentan empates en estos rangos suelen saltar estas advertencias. La función wilcoxsign_test() del paquete coin permite realizar esta prueba con correción para empates.

library(coin)

wilcoxsign_test(ls ~ as.numeric(group), data = boneden_long)

    Asymptotic Wilcoxon-Pratt Signed-Rank Test

data:  y by x (pos, neg) 
     stratified by block
Z = -7.834, p-value = 4.725e-15
alternative hypothesis: true mu is not equal to 0

Vemos que los resultados cambian porque se ha usado otra versión de la prueba para manejar los empates.

También podemos realizar esta prueba usando el paquete rstatix.

boneden_long %>% 
  wilcox_test(
    ls ~ group, paired = TRUE, alternative = "two.sided", mu = 0, detailed = TRUE
  )
# A tibble: 1 × 12
  estimate .y.   group1 group2    n1    n2 statistic      p conf.low conf.high
*    <dbl> <chr> <chr>  <chr>  <int> <int>     <dbl>  <dbl>    <dbl>     <dbl>
1   0.0400 ls    ls1    ls2       41    41      618. 0.0156  0.00998    0.0650
# ℹ 2 more variables: method <chr>, alternative <chr>

Un problema con esta función es que no bota la advertencia de empates. Si bien es solo una advertencia y no quiere decir que la prueba esté mal, es importante estar al tanto de las limitaciones en nuestro análisis.

10.6 Pruebas de más de dos
muestras independientes

Para este caso usaremos la data del caso de estudio de niveles de plomo en la sangre de niños, pero usaremos la variable lead_group que separa a los muestreados en tres grupos. Primero, transformaremos nuestra variable lead_group en un factor.

lead <- lead %>%
  mutate(lead_grp = factor(lead_grp))

10.6.1 ANOVA

Supuestos:

  • Más de 2 muestras aleatorias simples.
  • La variable dependiente tiene una distribución normal en cada población.
  • La varianza de la variable dependiente es igual en todas las poblaciones (homocedasticidad).

En el caso de más de dos muestras independientes, se utiliza la técnica del análisis de varianza (ANOVA). Se puede pensar esta técnica como la generalización para más de dos muestras de la prueba t. También asume normalidad, pero sobre los residuales luego de haber ajustado las fuentes de variabilidad, además de homogeneidad de varianzas (homocedasticidad).

Graficaremos los datos del puntaje de IQ (de performance de codificación) (iqp_cod) para comprender la distribución de datos.

lead %>%
  ggplot(aes(x = lead_grp, y = iqp_cod)) +
  geom_boxplot() + 
  stat_summary(fun = mean, color = "red")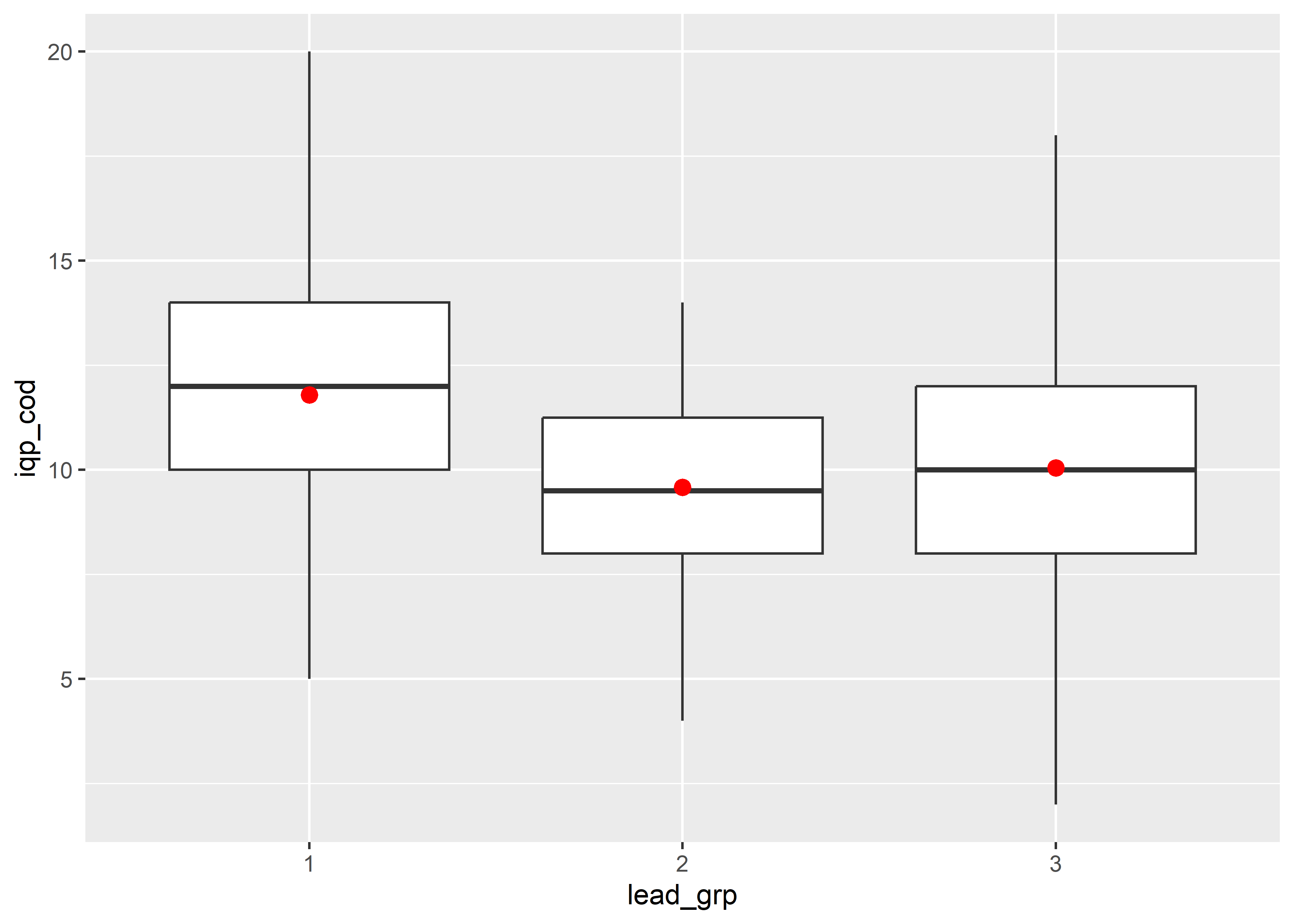

La función base en R para realizar el ANOVA es aov().

iqf_aov <- aov(iqp_cod ~ lead_grp, data = lead)
summary(iqf_aov)
             Df Sum Sq Mean Sq F value  Pr(>F)   
lead_grp      2  117.1   58.55   5.554 0.00492 **
Residuals   121 1275.5   10.54                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

También podemos usar la función anova_test() del paquete rstatix.

lead %>% 
  anova_test(iqp_cod ~ lead_grp)
ANOVA Table (type II tests)

    Effect DFn DFd     F     p p<.05   ges
1 lead_grp   2 121 5.554 0.005     * 0.084

Vemos de los resultados que existe evidencia suficiente para decir que las medias del puntaje de IQ (de performance de codificación) entre los grupos (al menos 1) son diferentes.

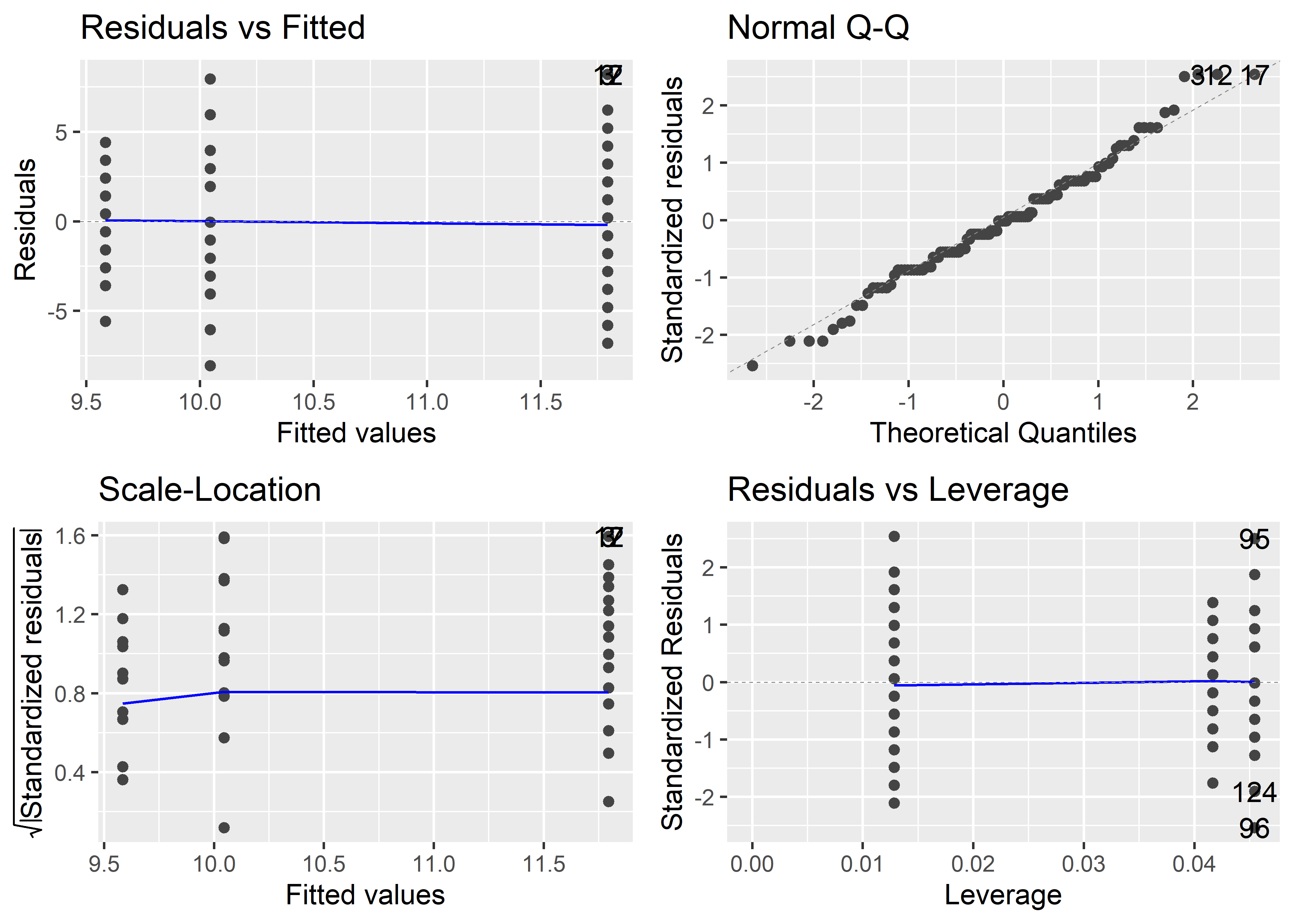
Podemos evaluar los supuestos llamando al paquete ggfortify y usando la función autoplot(), que genera gráficos al estilo de gplot2.

Se observa que los residuales parecen cumplir con los supuestos de normalidad y homocedasticidad anteriormente comentados.

10.6.1.1 Prueba de comparación entre pares

Para determinar cuál de los tres grupos difiere significativamente de los demás utilizamos la prueba post-hoc de Bonferroni. El paquete rstatix provee la función emmeans_test.

lead %>% 
  emmeans_test(iqp_cod ~ lead_grp, p.adjust.method = "bonferroni")
# A tibble: 3 × 9
  term     .y.     group1 group2    df statistic       p  p.adj p.adj.signif
* <chr>    <chr>   <chr>  <chr>  <dbl>     <dbl>   <dbl>  <dbl> <chr>       
1 lead_grp iqp_cod 1      2        121     2.92  0.00420 0.0126 *           
2 lead_grp iqp_cod 1      3        121     2.23  0.0275  0.0824 ns          
3 lead_grp iqp_cod 2      3        121    -0.482 0.631   1      ns

Podemos observar diferencias significativas entre el grupo 1 y 2.

El paquete rstatix provee la función tukey_hsd para un ajuste de pruebas multiples menos conservador.

lead %>% 
  tukey_hsd(iqp_cod ~ lead_grp)
# A tibble: 3 × 9
  term  group1 group2 null.value estimate conf.low conf.high  p.adj p.adj.signif
* <chr> <chr>  <chr>       <dbl>    <dbl>    <dbl>     <dbl>  <dbl> <chr>       
1 lead… 1      2               0   -2.21     -4.01    -0.413 0.0116 *           
2 lead… 1      3               0   -1.75     -3.61     0.110 0.0699 ns          
3 lead… 2      3               0    0.462    -1.81     2.74  0.88   ns

10.6.2 Kruskal-Wallis

Si alguno de los supuestos de ANOVA de un solo sentido no se cumple, se suele usar la prueba no paramétrica de Kruskal-Wallis.

lead %>%
  ggplot(aes(x = lead_grp, y = iqf)) +
  geom_boxplot() + 
  stat_summary(fun = mean, color = "red")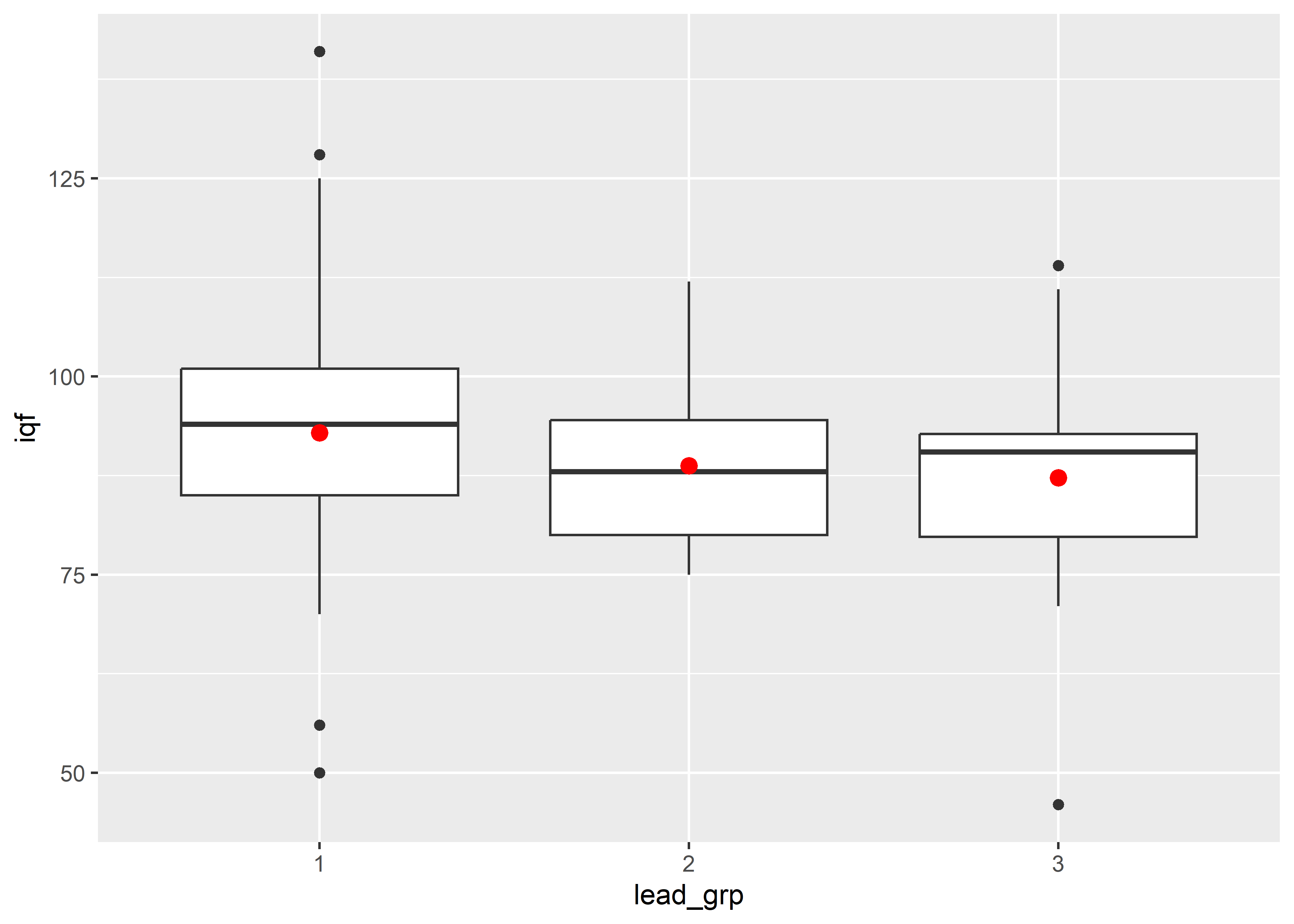

Para realizar esta prueba, podemos usar la función kruskal_test() del paquete rstatix.

lead %>% 
  kruskal_test(iqf ~ lead_grp)
# A tibble: 1 × 6
  .y.       n statistic    df     p method        
* <chr> <int>     <dbl> <int> <dbl> <chr>         
1 iqf     124      3.36     2 0.187 Kruskal-Wallis

10.6.2.1 Prueba de comparación entre pares

En el caso no-paramétrico, podemos usar la prueba de Dunn para hacer comparaciones entre pares. Podemos realizar esta prueba con la función dunn_test() del paquete rstatix.

lead %>% 
  dunn_test(iqf ~ lead_grp)
# A tibble: 3 × 9
  .y.   group1 group2    n1    n2 statistic     p p.adj p.adj.signif
* <chr> <chr>  <chr>  <int> <int>     <dbl> <dbl> <dbl> <chr>       
1 iqf   1      2         78    24    -1.40  0.163 0.421 ns          
2 iqf   1      3         78    22    -1.47  0.140 0.421 ns          
3 iqf   2      3         24    22    -0.102 0.919 0.919 ns

10.7 Análisis de correlación

La correlación se refiere a cualquier relación o asociación estadística entre variables. La más sencilla de definir, y también la más útil, es la correlación lineal. La correlación lineal describe qué tanto la relación entre dos variables puede representarse gráficamente con una línea.

La medida más comunmente usada es el coeficiente de correlación de Pearson, el cual se define como la razón entre la covarianza y el producto de las desviaciones estándar entre dos variables. Usando datos observados, el coeficiente de correlación de Pearson suele representarse por la letra \(r\). Sus valores varían de -1 a 1, donde los valores negativos indican una asociación inversa y los valores positivos una asociación directa. La magnitud del coeficiente de correlación, \(|r|\), indica qué tan fuerte es la relación. Una magnitud de 0 indica que no existe relación alguna, mientras que una magnitud de 1 indica una asociación perfectamente lineal.

Una versión no paramétrica del coeficiente de correlación de Pearson es el coeficiente de correlación de rangos de Spearman, el cual está basado, como su nombre lo dice, en la asociación de los rangos de las variables. No obstante, el coeficiente de correlación de Spearman no mide si la asociación es lineal, solo si es monótona. Suele representarse, para muestras, como \(r_{s}\) y, al igual que \(|r|\), varía de -1 a 1.

10.7.1 Análisis descriptivo

Para esta sección de análisis de correlación usaremos el conjunto de datos mtcars que viene con el paquete base de R.

La función base cor() permite calcular la matriz de correlación de un conjunto de datos:

mtcars %>% 
  select(mpg, disp, hp, drat, wt, qsec) %>% 
  cor()
            mpg       disp         hp        drat         wt        qsec
mpg   1.0000000 -0.8475514 -0.7761684  0.68117191 -0.8676594  0.41868403
disp -0.8475514  1.0000000  0.7909486 -0.71021393  0.8879799 -0.43369788
hp   -0.7761684  0.7909486  1.0000000 -0.44875912  0.6587479 -0.70822339
drat  0.6811719 -0.7102139 -0.4487591  1.00000000 -0.7124406  0.09120476
wt   -0.8676594  0.8879799  0.6587479 -0.71244065  1.0000000 -0.17471588
qsec  0.4186840 -0.4336979 -0.7082234  0.09120476 -0.1747159  1.00000000

Otra función que permite obtener matrices más al estilo de tidyverse es la función cor_mat() del paquete rstatix:

mtcars %>% 
  select(mpg, disp, hp, drat, wt, qsec) %>% 
  cor_mat()
# A tibble: 6 × 7
  rowname   mpg  disp    hp   drat    wt   qsec
* <chr>   <dbl> <dbl> <dbl>  <dbl> <dbl>  <dbl>
1 mpg      1    -0.85 -0.78  0.68  -0.87  0.42 
2 disp    -0.85  1     0.79 -0.71   0.89 -0.43 
3 hp      -0.78  0.79  1    -0.45   0.66 -0.71 
4 drat     0.68 -0.71 -0.45  1     -0.71  0.091
5 wt      -0.87  0.89  0.66 -0.71   1    -0.17 
6 qsec     0.42 -0.43 -0.71  0.091 -0.17  1

Es posible también pasar las variables que se van a analizar a la misma función cor_mat():

mtcars %>% 
  cor_mat(mpg, disp, hp, drat, wt, qsec)
# A tibble: 6 × 7
  rowname   mpg  disp    hp   drat    wt   qsec
* <chr>   <dbl> <dbl> <dbl>  <dbl> <dbl>  <dbl>
1 mpg      1    -0.85 -0.78  0.68  -0.87  0.42 
2 disp    -0.85  1     0.79 -0.71   0.89 -0.43 
3 hp      -0.78  0.79  1    -0.45   0.66 -0.71 
4 drat     0.68 -0.71 -0.45  1     -0.71  0.091
5 wt      -0.87  0.89  0.66 -0.71   1    -0.17 
6 qsec     0.42 -0.43 -0.71  0.091 -0.17  1

Para génerar gráficos a partir de la matriz de correlación, podemos usar la función cor_plot(). Primero podemos guardar la matriz en un objeto, y luego pasarlo a cor_plot():

corr_mat <- mtcars %>% 
  cor_mat(mpg, disp, hp, drat, wt, qsec)

corr_mat %>% cor_plot()

Si queremos graficar solo el triángulo superior o inferior de la matriz, podemos usar las funciones pull_upper_triangle() y pull_lower_triangle(), respectivamente. Por ejemplo:

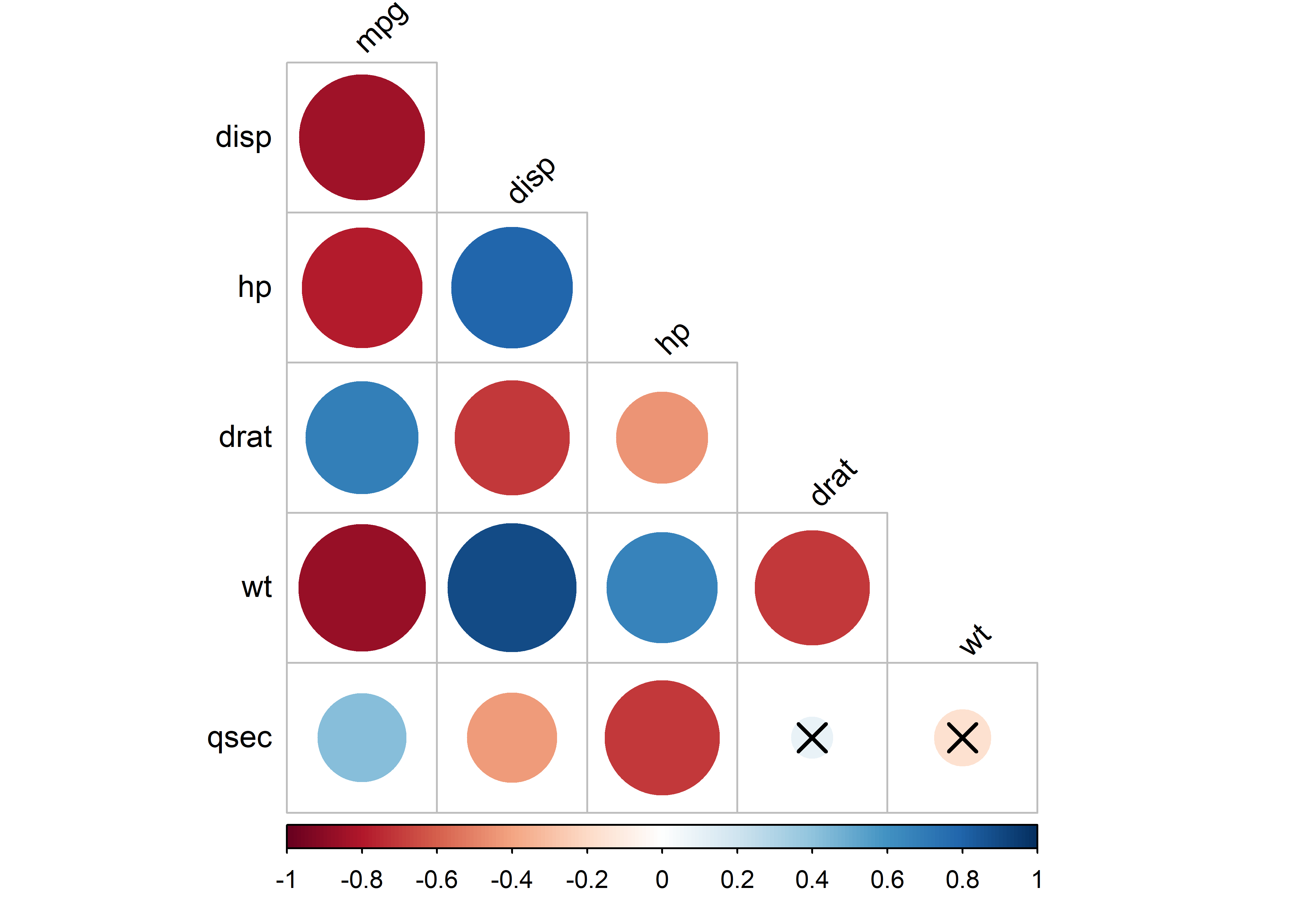
Si queremos mostrar los valores de correlación en el gráfico, podemos incluir el argumento method = "number" en la función cor_plot():

corr_mat %>% 
  pull_lower_triangle() %>% 
  cor_plot(method = "number")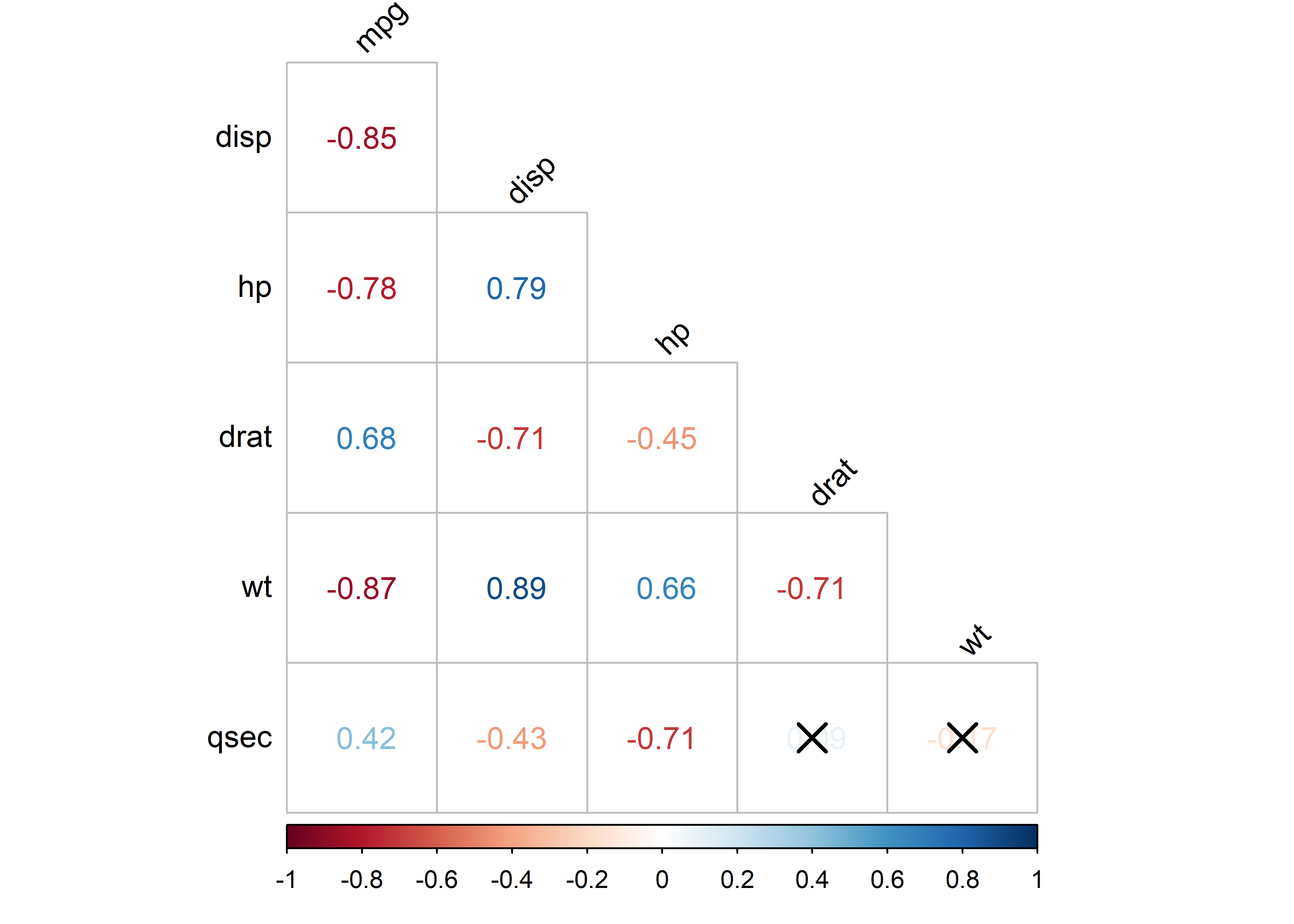

Para describir la asociación de un conjunto de datos usando la correlación lineal (de Pearson), es recomendable usar una ayuda gráfica, ya que como mencionamos esta mide qué tanto la asociación entre variables se puede representar por una línea.

Para usar la correlación de Spearman, podemos pasar el argumento method = "spearman" a la función cor_mat():

corr_mat_spear <- mtcars %>% 
  cor_mat(mpg, disp, hp, drat, wt, qsec, method = "spearman")

corr_mat_spear %>% 
  pull_lower_triangle() %>% 
  cor_plot(method = "number")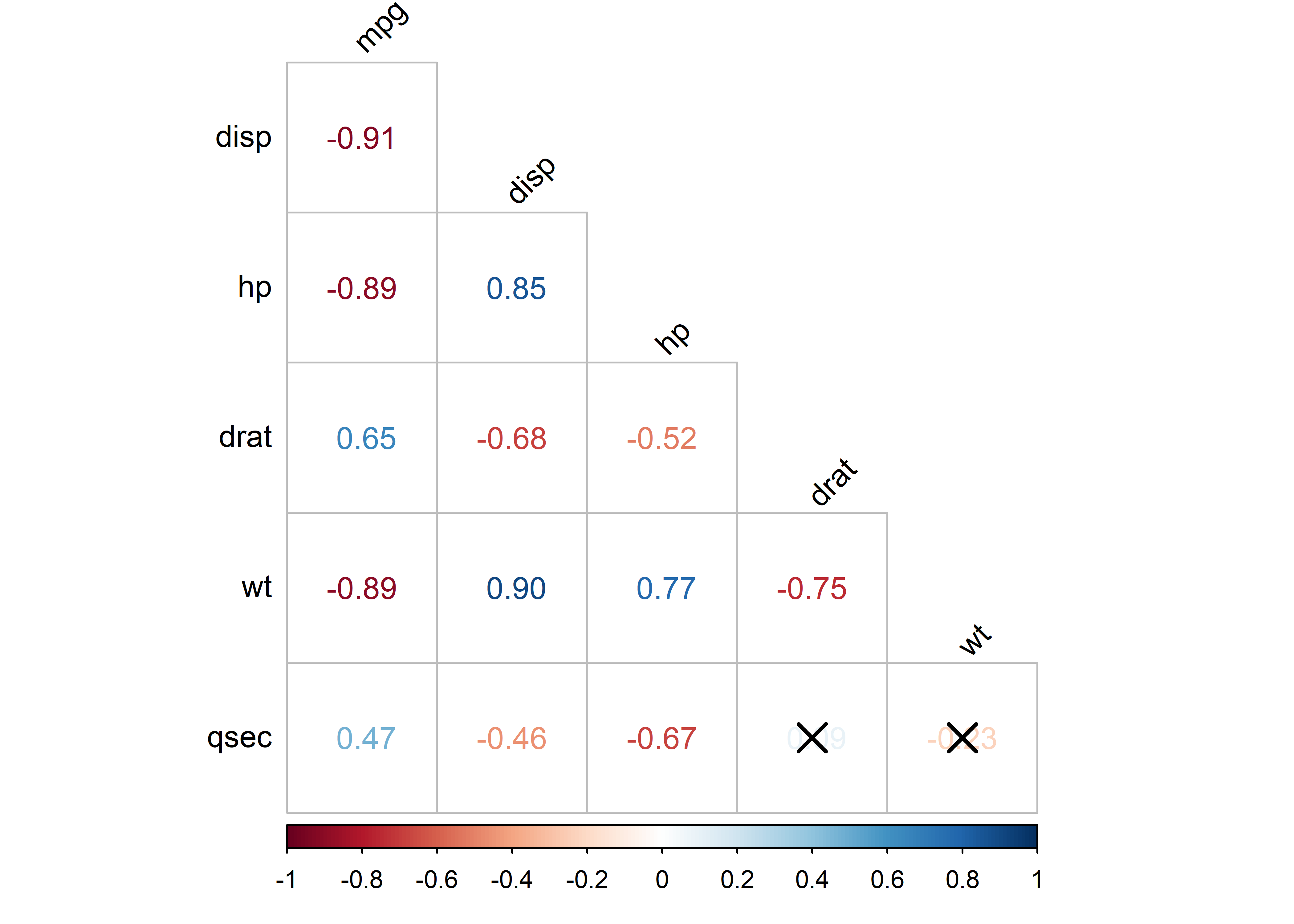

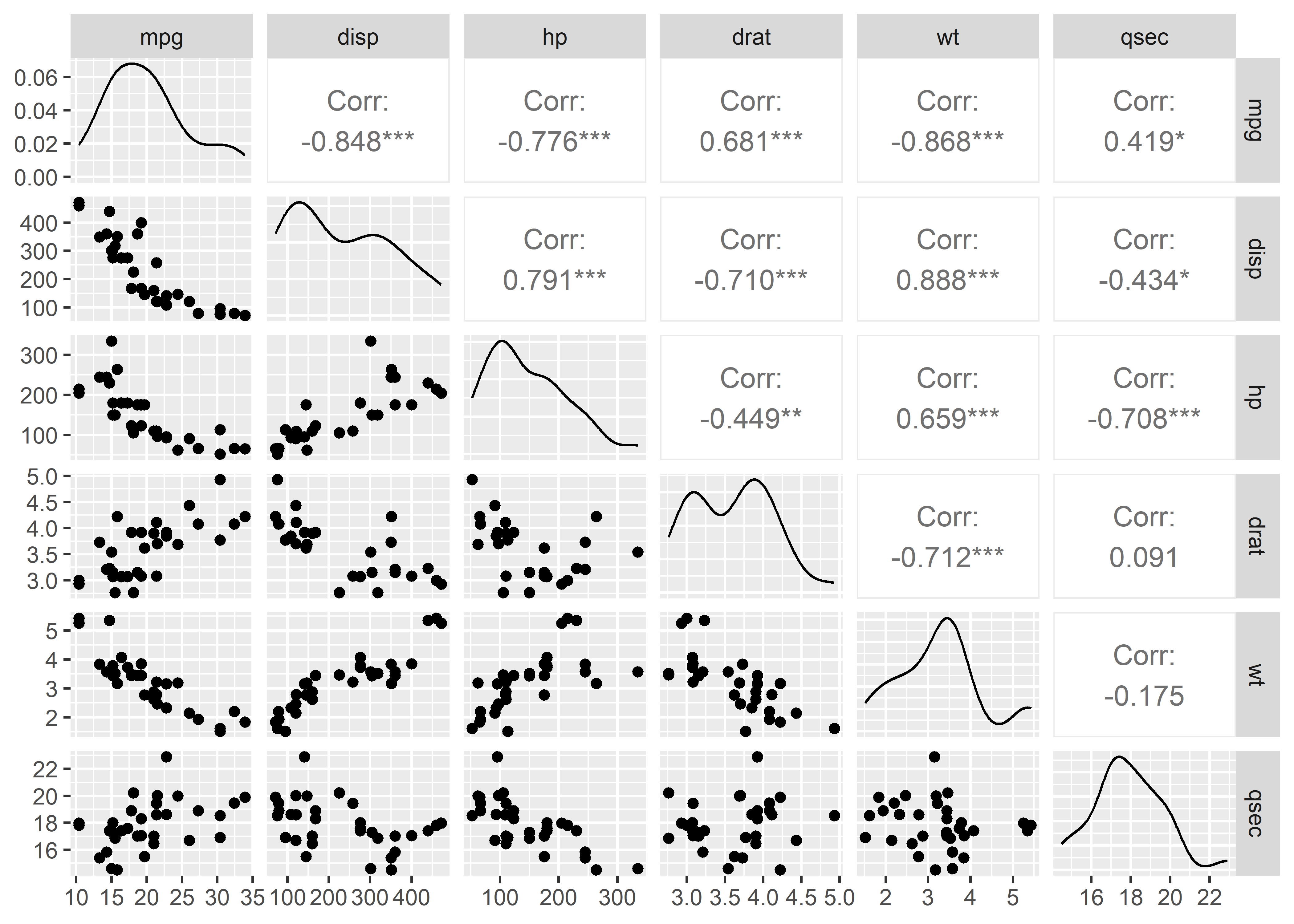
Otra función bastante útil que permite generar gráficos de matriz de correlaciones es la función ggpairs() del paquete GGally. Esta función genera también gráficos de dispersión entre las variables para así poder evaluar visualmente si la asociación entre ellas parece ser lineal o no:

library(GGally)

mtcars %>%
  select(mpg, disp, hp, drat, wt, qsec) %>% 
  ggpairs(progress = FALSE)

Además, muestra los coeficientes de correlación y sus códigos de significancia (*).

10.7.2 Prueba de significancia

La prueba de significancia del coeficiente de correlación de Pearson se usa para verificar que la asociación lineal sea estadísticamente significativa. Esta prueba asume que las dos muestras provienen de distribuciones normales.

Para realizar la prueba de significancia para el coeficiente de correlación de Pearson podemos usar la función base cor.test() de la siguiente manera:

cor.test(mtcars$mpg, mtcars$hp)

    Pearson's product-moment correlation

data:  mtcars$mpg and mtcars$hp
t = -6.7424, df = 30, p-value = 1.788e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.8852686 -0.5860994
sample estimates:
       cor 
-0.7761684

Por su lado, la función cor_test() del paquete rstatix nos permite realizar la prueba sobre todas las combinaciones de variables del data frame que le pasemos:

mtcars %>% 
  cor_test(mpg, disp, hp, drat, wt, qsec)
# A tibble: 36 × 8
   var1  var2    cor statistic        p conf.low conf.high method 
   <chr> <chr> <dbl>     <dbl>    <dbl>    <dbl>     <dbl> <chr>  
 1 mpg   mpg    1       Inf    0          1          1     Pearson
 2 mpg   disp  -0.85     -8.75 9.38e-10  -0.923     -0.708 Pearson
 3 mpg   hp    -0.78     -6.74 1.79e- 7  -0.885     -0.586 Pearson
 4 mpg   drat   0.68      5.10 1.78e- 5   0.436      0.832 Pearson
 5 mpg   wt    -0.87     -9.56 1.29e-10  -0.934     -0.744 Pearson
 6 mpg   qsec   0.42      2.53 1.71e- 2   0.0820     0.670 Pearson
 7 disp  mpg   -0.85     -8.75 9.38e-10  -0.923     -0.708 Pearson
 8 disp  disp   1       Inf    0          1          1     Pearson
 9 disp  hp     0.79      7.08 7.14e- 8   0.611      0.893 Pearson
10 disp  drat  -0.71     -5.53 5.28e- 6  -0.849     -0.481 Pearson
# ℹ 26 more rows

Por otro lado, si queremos realizar pruebas de significancia para el coeficiente de correlación de Spearman, podemos pasar el argumento method = "spearman":

mtcars %>% 
  cor_test(mpg, disp, hp, drat, wt, qsec, method = "spearman")
# A tibble: 36 × 6
   var1  var2    cor statistic        p method  
   <chr> <chr> <dbl>     <dbl>    <dbl> <chr>   
 1 mpg   mpg    1           0  0        Spearman
 2 mpg   disp  -0.91    10415. 6.37e-13 Spearman
 3 mpg   hp    -0.89    10337. 5.09e-12 Spearman
 4 mpg   drat   0.65     1902. 5.38e- 5 Spearman
 5 mpg   wt    -0.89    10292. 1.49e-11 Spearman
 6 mpg   qsec   0.47     2908. 7.06e- 3 Spearman
 7 disp  mpg   -0.91    10415. 6.37e-13 Spearman
 8 disp  disp   1           0  0        Spearman
 9 disp  hp     0.85      813. 6.79e-10 Spearman
10 disp  drat  -0.68     9186. 1.61e- 5 Spearman
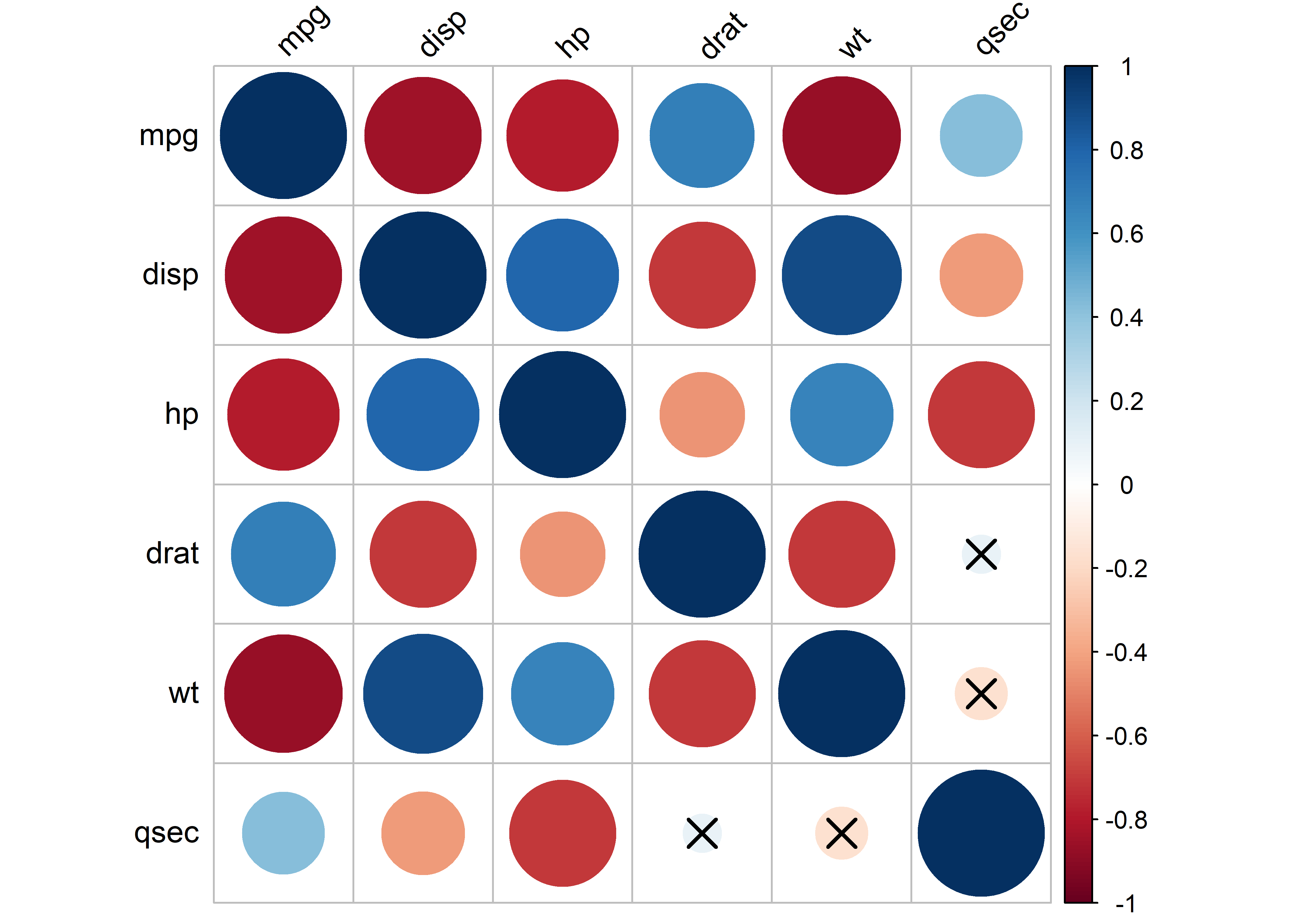
# ℹ 26 more rows

En los gráficos, las correlaciones que no son significativas se marcan con una X. Por ejemplo, generemos otro gráfico para las correlaciones de Spearman. En este caso, pasaremos el argumento method = "color" a la función cor_plot() para que rellene cada cuadrado de color:

corr_mat_spear %>% 
  pull_lower_triangle() %>% 
  cor_plot(method = "color")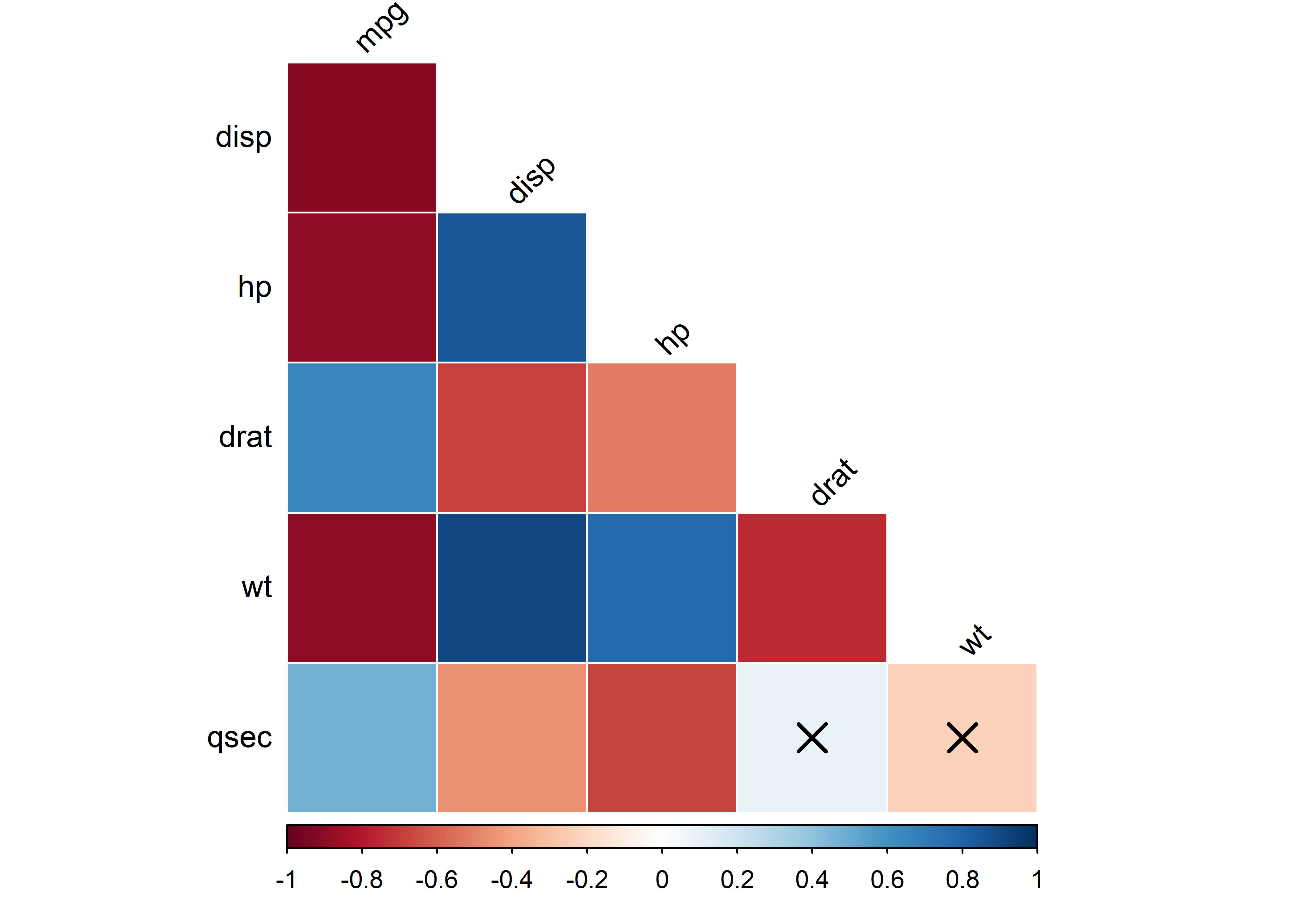

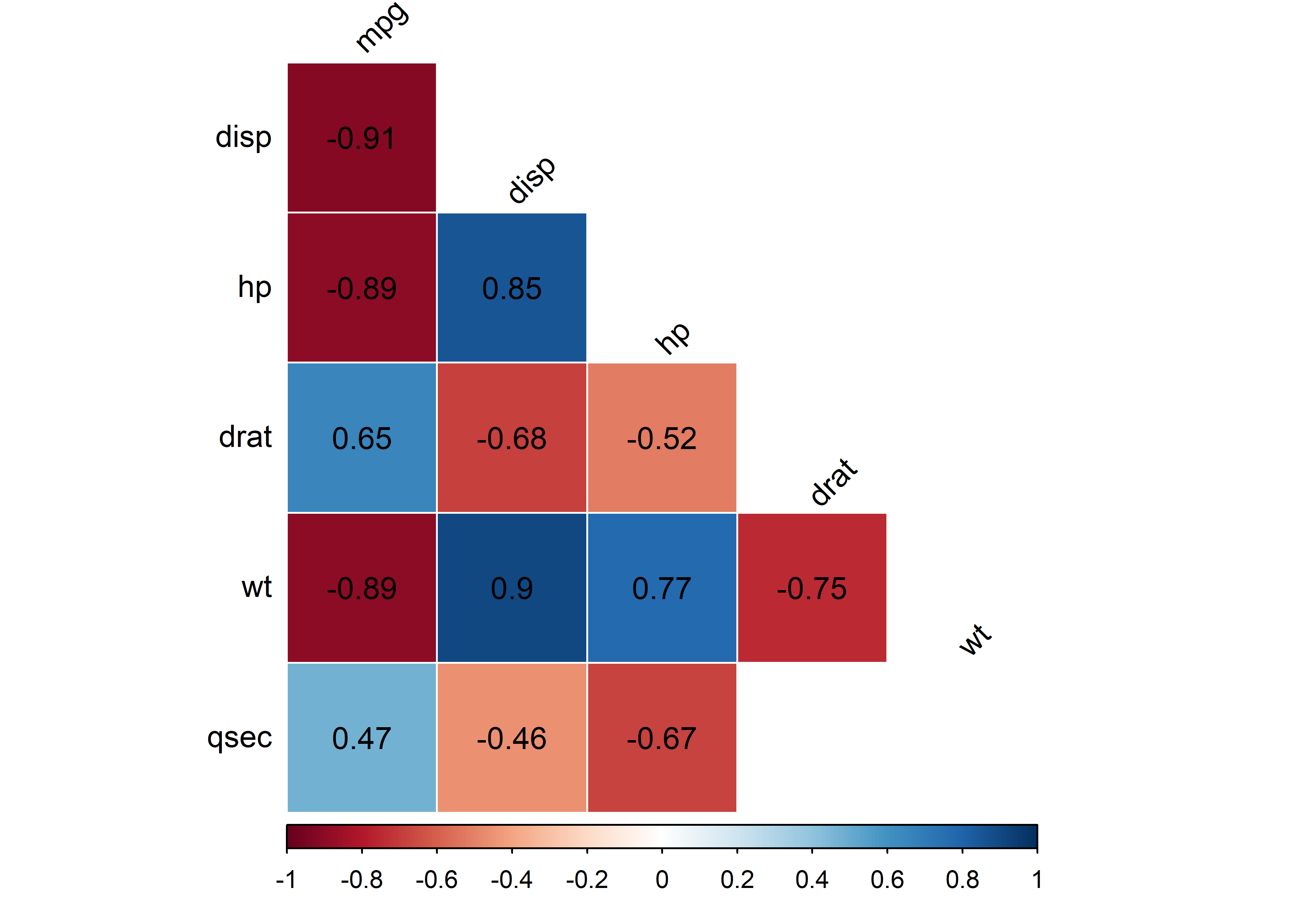
También podemos agregar el coeficiente de correlación pasando label = TRUE. Si queremos que en vez de tachar pinte de blanco las correlaciones no significativamos, podemos pasar insignificant = "blank":

corr_mat_spear %>% 
  pull_lower_triangle() %>% 
  cor_plot(
    method = "color",
    label = TRUE,
    insignificant = "blank"
  )

Otro paquete que podría ser de utilidad para la generación de gráficos de correlación dinámicos es heatmaply.

10.8 Ejercicios

Para los ejercicios 1 y 2 usaremos el conjunto de datos ToothGrowth. Cargaremos este conjunto de datos en un objeto llamado tooth usando las siguientes línea:

tooth <- ToothGrowth

Con la función glimpse, podemos darle un vistazo a la data:

glimpse(tooth)
Rows: 60
Columns: 3
$ len  <dbl> 4.2, 11.5, 7.3, 5.8, 6.4, 10.0, 11.2, 11.2, 5.2, 7.0, 16.5, 16.5,…
$ supp <fct> VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, VC, V…
$ dose <dbl> 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 1.0, 1.0, 1.0, …

Este conjunto de datos proviene de una investigación en donde se quería medir el efecto de la vitamina C en el crecimiento de los dientes de los conejillos de indias. La variable de respuesta es la longitud (len) del odontoblasto en 60 conejillos de indias. Cada uno de ellos recibió un de las tres dosis (dose) de vitamina C (0.5, 1, and 2 mg/día) mediante uno de dos métodos de suplementación (supp), jugo de naranja (OJ) o ácido ascórbico (VC).

Ejercicio 1

Usar las pruebas de dos muestras independientes para verificar si la longitud del odontoblasto de los conejillos de indias fue significativamente diferente entre los recibieron la suplementación por jugo de naranja y los que recibieron suplementación por ácido ascórbico. En el caso que corresponda, realizar el análisis respectivo de los supuestos de la prueba.

Ejercicio 2

Usar las pruebas de más de dos muestras independientes para verificar si la longitud del odontoblasto de los conejillos de indias difiere significativamente según la dosis de vitamina C que se les administró. En el caso que corresponda, realizar el análisis respectivo de los supuestos de la prueba. Además, comparar los grupos usando pruebas por pares.

Ejercicio 3

Para este ejercicio usaremos el conjunto de datos anorexia del paquete MASS.

library(MASS)
glimpse(anorexia)
Rows: 72
Columns: 3
$ Treat  <fct> Cont, Cont, Cont, Cont, Cont, Cont, Cont, Cont, Cont, Cont, Con…
$ Prewt  <dbl> 80.7, 89.4, 91.8, 74.0, 78.1, 88.3, 87.3, 75.1, 80.6, 78.4, 77.…
$ Postwt <dbl> 80.2, 80.1, 86.4, 86.3, 76.1, 78.1, 75.1, 86.7, 73.5, 84.6, 77.…

En este conjunto de datos, se evalúa el cambio en peso en libras de 72 mujeres jóvenes con anorexia antes (Prewt) y después (Postwt) de uno de tres posibles tratamientos (Treat).

Transformar la data en formato long y evaluar si hay una diferencia significativa entre el peso antes y después del tratamiento usando la prueba correspondiente. Si fuera el caso, examinar los supuestos de la prueba.