23  Análisis de inequidad

Autores/as

Carrasco Escobar, Gabriel

Quispe Quispe, Jesus

23.1 Motivación

En este capítulo abordaremos métricas de la ausencia de igualdad ( desigualdad) y equidad ( inequidad). La igualdad significa que cada individuo o grupo de personas recibe los mismos recursos u oportunidades. La equidad reconoce que cada persona tiene circunstancias diferentes y asigna los recursos y oportunidades exactos necesarios para alcanzar un resultado igualitario. En el contexto de la salud, estas diferencias pueden manifestarse en términos de morbilidad, mortalidad, acceso a tratamientos médicos, prevención de enfermedades, etc. (Wagstaff et al. 2007).

Equidad e Igualdad. Adaptado de Robert Wood Johnson Foundation.

23.1.1 Desigualdad

Podemos entender la igualdad de la siguiente manera. Imaginemos un grupo de distritos (con la misma cantidad de población cada uno) donde todos tienen la misma cantidad de casos de una enfermedad.

library(tidyverse)

g1 <- tibble(id = paste("A", 11:60, sep = ""), 
             cases = 30)

g1 %>%
  ggplot(aes(x = id, y = cases)) +
  geom_bar(stat="identity") +
  theme_bw()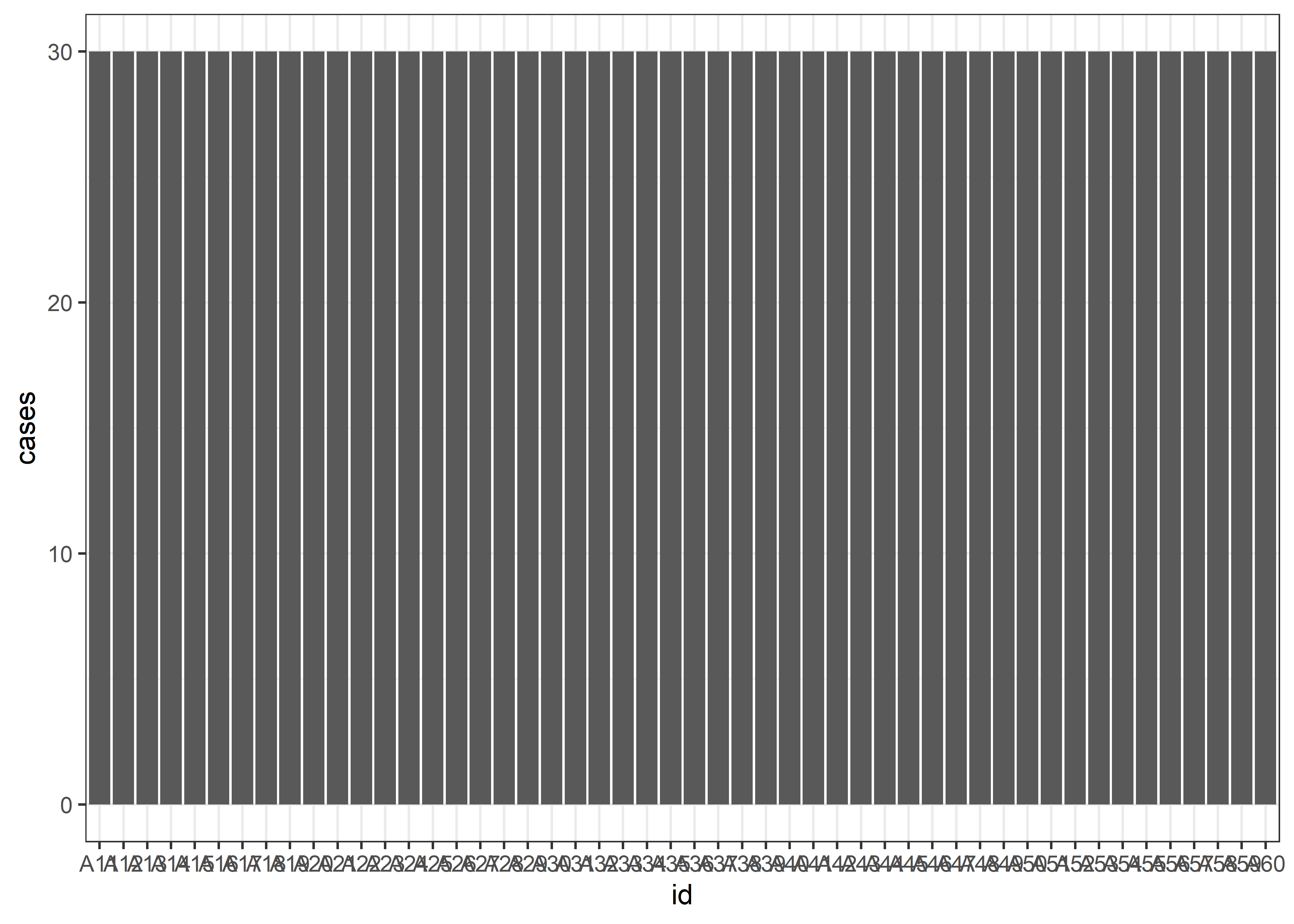

En este caso, cada distrito equivale al 2% de la población (1/50). Bajo el supuesto de que exite igualdad esperamos que el numero de casos de cada distrito corresponda al 2% del total de casos.

Las métricas de desigualdad buscan expresar las diferencias en asignación de una caracteristica (riqueza, enfermedad, etc.) y en consecuencia se hace un ranking de individuos (o pueden ser otras unidad como ciudades, paises, etc.) de menor a mayor asignación de la caracteristica de interés. Esto lo realizaremos con la función arrange() para posteriormente calcular la acumulación relativa de los individuos y la característica. En este escenario calcularemos la acumulación relativa de los distritos y los casos.

g1_s <- g1 %>%
  arrange(cases) %>%
  mutate(pop = 1,
         r_cum_pop = cumsum(pop) / sum(pop) ,
         r_cum_cases  = cumsum(cases) / sum(cases))

tibble(r_cum_pop = 0, r_cum_cases = 0) %>% # agregamos el punto de partida
  bind_rows(g1_s) %>% 
  ggplot(aes(x = r_cum_pop, y = r_cum_cases)) +
  geom_point(col = "red") +
  geom_path(col="red") +
  geom_abline() + # linea de igualdad
  theme_bw() + 
  labs(y = "Proporción acumulada de casos",
       x = "Proporción acumulada de población rankeado por casos")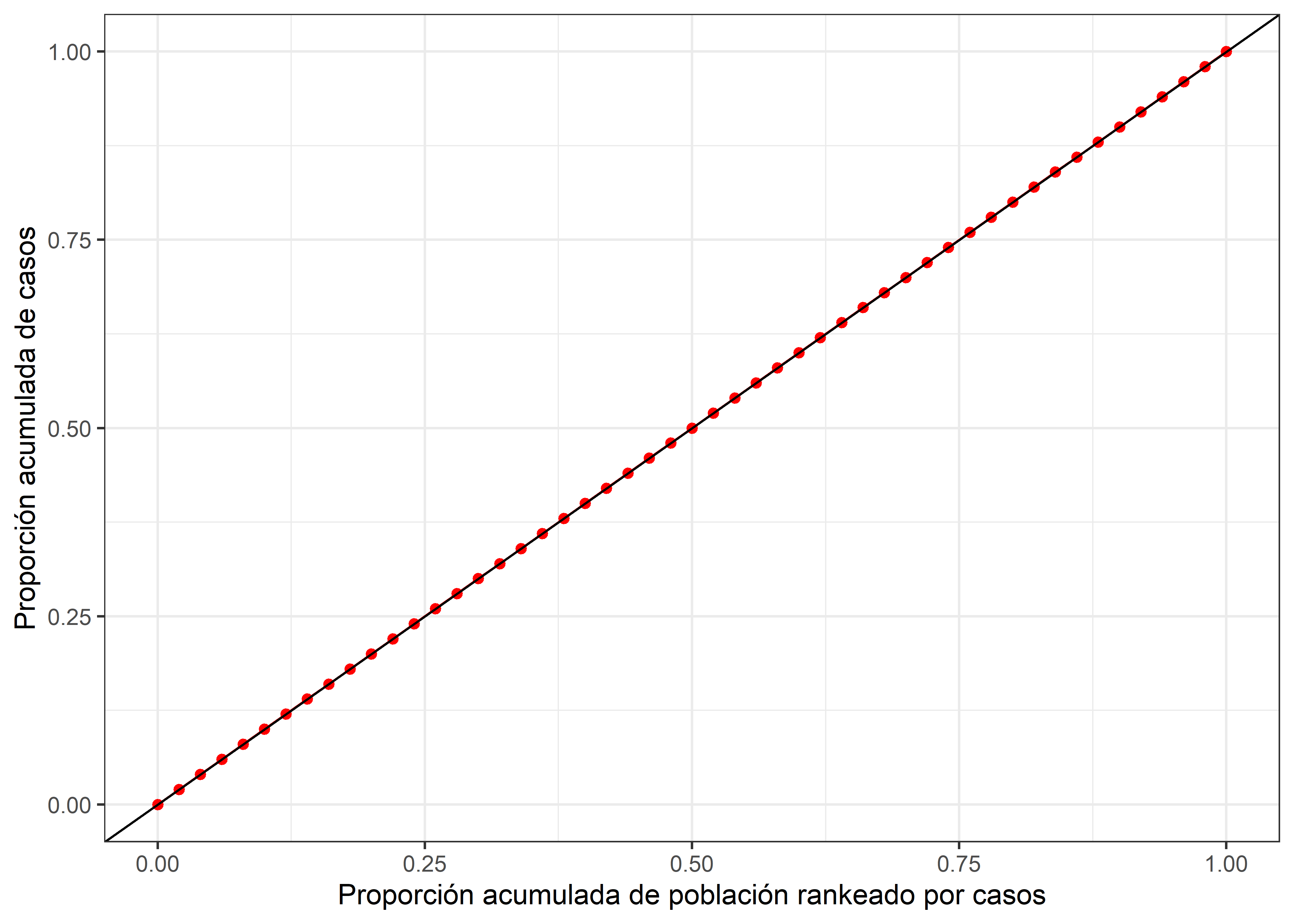

Como observamos, un aumento porcentual en la acumulación de distritos equivale al mismo aumento porcentual en la acumulación de casos. Es decir, sigue la linea de igualdad. En este caso podemos decir que en esta población de distritos existe igualdad de la cantidad de casos.

Ahora, exploraremos un escenario donde no todos los distritos tienen la misma cantidad de casos.

g2 <- tibble(id = paste("A", 11:60, sep=""),
             cases = round(rbeta(50, .1, 1),3)*1000)
g2 %>%
  ggplot(aes(x = id, y = cases)) +
  geom_bar(stat="identity") +
  theme_bw()

g2_s <- g2 %>%
  arrange(cases) %>%
  mutate(pop = 1,
         r_cum_pop = cumsum(pop) / sum(pop) ,
         r_cum_cases  = cumsum(cases) / sum(cases))

tibble(r_cum_pop = 0, r_cum_cases = 0) %>% # agregamos el punto de partida
  bind_rows(g2_s) %>% 
  ggplot(aes(x = r_cum_pop, y = r_cum_cases)) +
  geom_point(col = "red") +
  geom_path(col="red") +
  geom_abline() + # linea de igualdad
  theme_bw() +
  labs(y = "Proporción acumulada de casos",
       x = "Proporción acumulada de población rankeado por casos")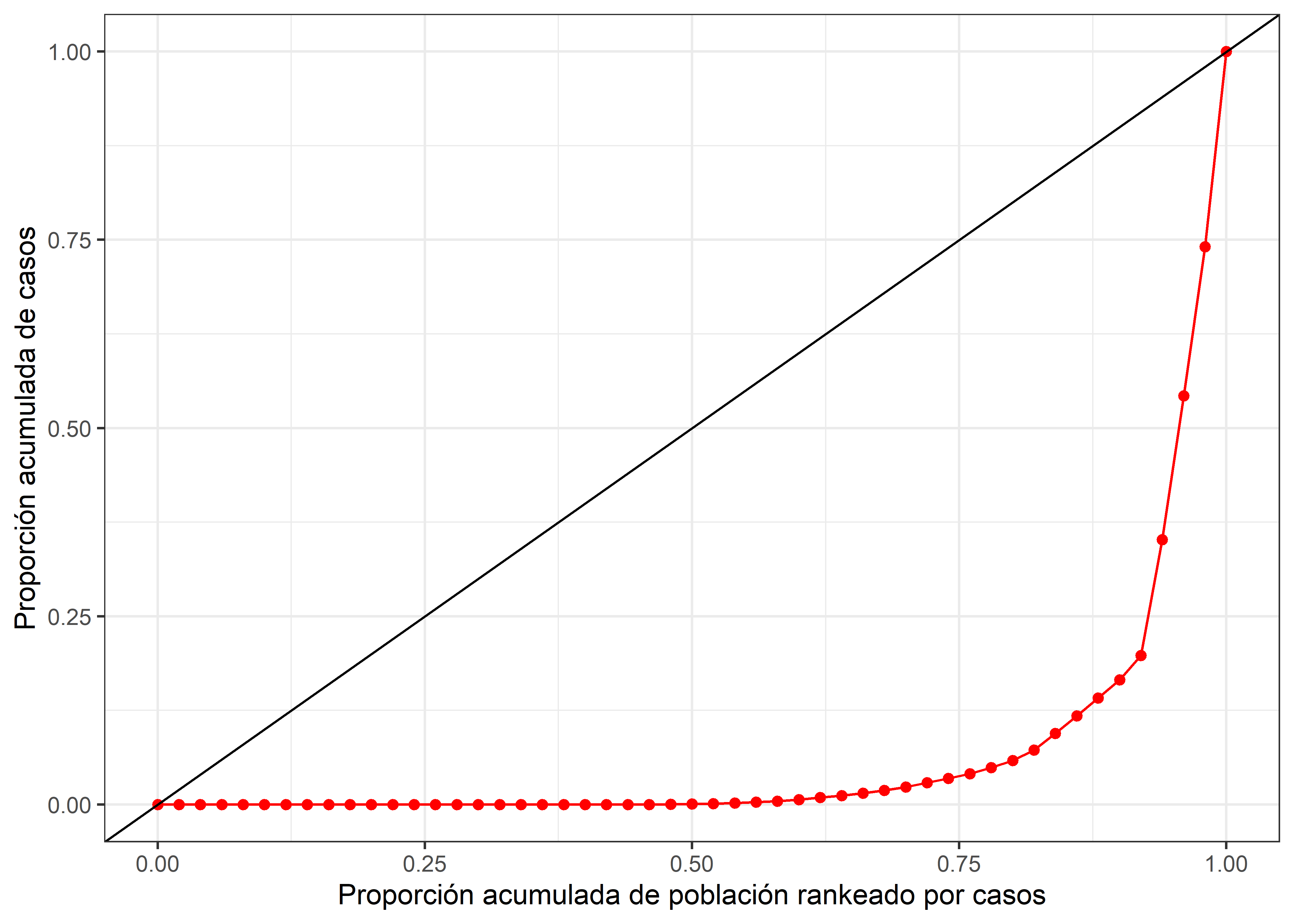

En este caso observamos que la acumulación de población no sigue el mismo patron de acumulación de casos La línea roja se aleja de la linea de igualdad. En este capítulo calcularemos indicadores para determinar la magnitud de esta brecha (área entre la linea de igual y nuestra curva).

tibble(r_cum_pop = 0, r_cum_cases = 0) %>% # agregamos el punto de partida
  bind_rows(g2_s) %>% 
  ggplot(aes(x = r_cum_pop, y = r_cum_cases)) +
  geom_point(col = "red") +
  geom_path(col="red") +
  geom_ribbon(aes(ymin = r_cum_pop, ymax = r_cum_cases), fill = "red", alpha = 0.3) +
  geom_abline() + # linea de igualdad
  theme_bw() +
  labs(y = "Proporción acumulada de casos",
       x = "Proporción acumulada de población rankeado por casos")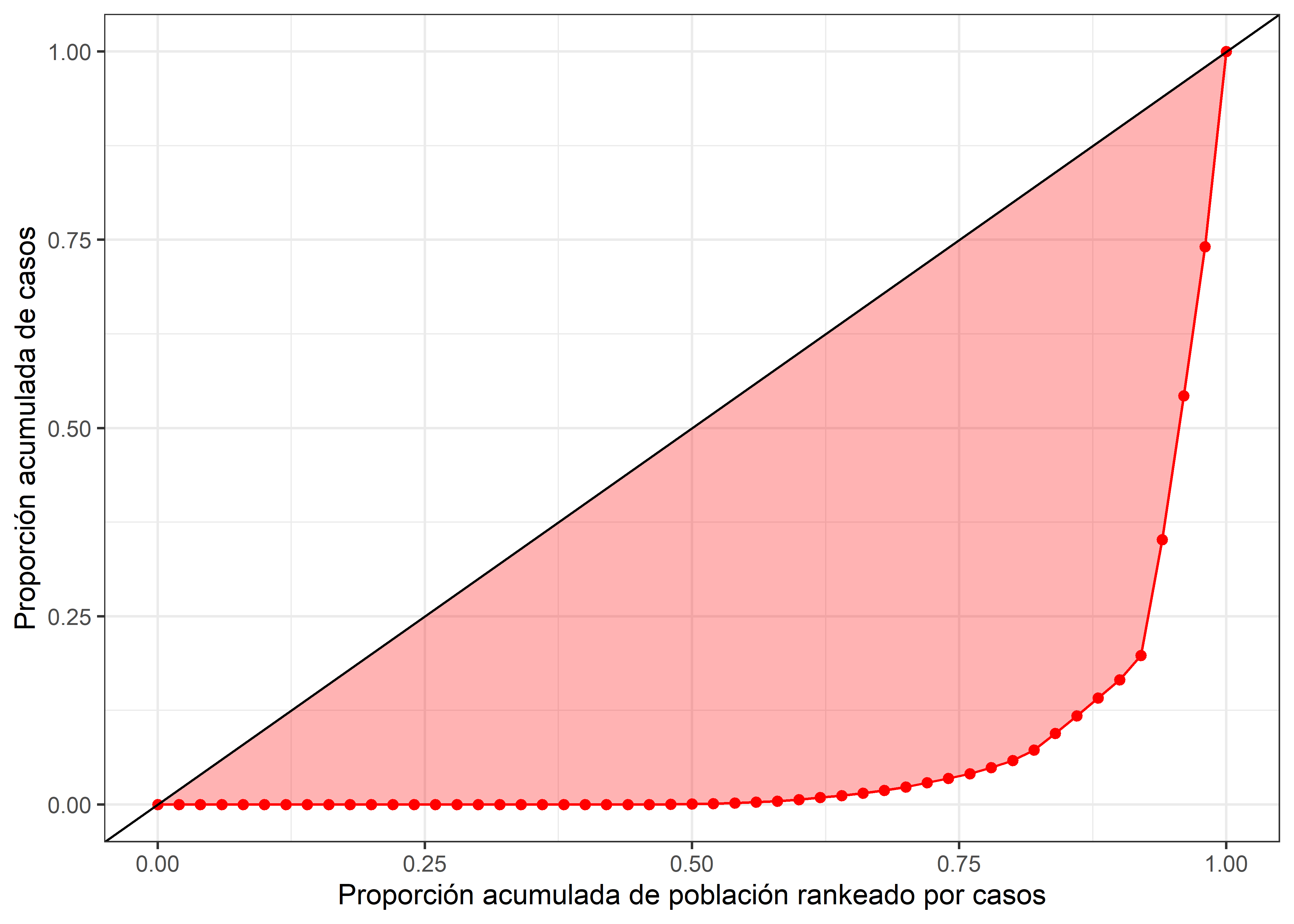

23.1.2 Inequidad

En la sección anterior hemos visto la intuición para medir la desigualdad. Sin embargo, las diferencias en asignación de una caracteristica pueden estar influenciados por otras variables. Cuando la característica de interés está relacionada con salud y las variables influyentes estan relacionadas a características socio-económicas, debemos considerar si estas diferencias son justas.

Para analizar equidad, el ranking no se hace en función a la asignación de la caracteristica de interés. En su lugar, el raking se hace en función a la variable socio-económica que influye es esas diferencias.

g3_s <- g2 %>%
  arrange(educ_yrs) %>%
  mutate(pop = 1,
         r_cum_pop = cumsum(pop) / sum(pop) ,
         r_cum_cases  = cumsum(cases) / sum(cases))

tibble(r_cum_pop = 0, r_cum_cases = 0) %>% # agregamos  punto de partida
  bind_rows(g3_s) %>%
  ggplot(aes(x = r_cum_pop, y = r_cum_cases)) +
  geom_point(col = "red") +
  geom_path(col="red") +
  geom_ribbon(aes(ymin = r_cum_pop, ymax = r_cum_cases), fill = "red", alpha = 0.3) +
  geom_abline() + # linea de igualdad
  theme_bw() +
  labs(y = "Proporción acumulada de casos",
       x = "Proporción acumulada de población rankeado por NSE")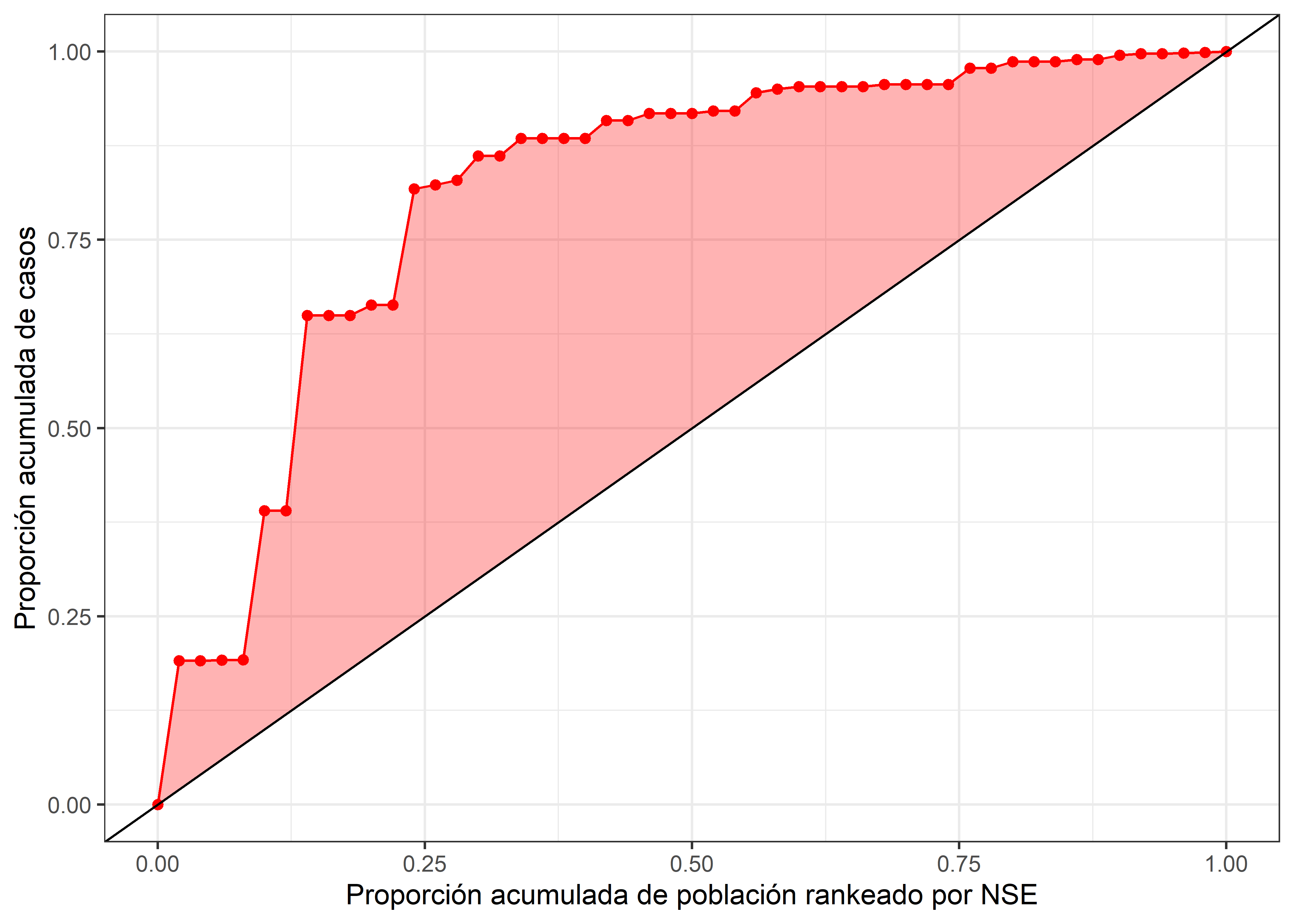

Con este análisis además de saber que los casos no estan distribuidos de forma homogenea en los distritos (igualdad), observamos que los casos estan concentrados en un grupo de distritos de bajo nivel socioeconomico (NSE). El 25% de los distritos con menor NSE concentran el 80% de casos.

Hay que reconocer que existe aún un debate sobre el uso de medidas que evalúan diferencias de salud entre diferentes categorías o valores de una característica socioeconómica porque implican, a su vez, un juicio moral. (Murray C. et al.)[https://pubmed.ncbi.nlm.nih.gov/10444876/]

23.1.3 Indicadores

Diferentes herramientas se han desarrollado para medir la desigualdad y la inequidad (Regidor 2004). Los indicadores que se revisarán en este capítulo son:

  1. Indicadores de desigualdad (en sentido estricto)

  2. Indicadores de Inequidad (Indicadores de desigualdad relativos a niveles socioeconomicos)

23.2 Caso de Estudio

Los anteriores indicadores seran reproducidos a traves del uso de una muestra de datos de la tasa de mortalidad materna recopilada para paises de América, compuesta del siguiente modo:

Etiqueta Descripcion
pobnv Número de nacidos vivos
pdbpc producto doméstico bruto per cápita, en $ internacionales constantes a un año base
rmm razón de mortalidad materna por 100.000 nacidos vivos
accsani % Personas que utilizan al menos servicios básicos de saneamiento
rtedu Tasa de finalización de educacion superior
capsalud Gasto en capital de salud (% PBI) 
library(tidyverse)

db <- read_csv("data/MortMaterna_latam.csv")

23.3 Indicadores de desigualdad (en sentido estricto)

23.3.1 Indice o Coeficiente de Gini

Mide la desigualdad en la distribucion de una determinada variable, y se calcula a partir de la curva de Lorenz.

La Curva de Lorenz: La curva de Lorenz es una representación gráfica de la distribución de la riqueza en una sociedad. En esta mediante una diagonal se representa la equidistribucion de la variable que se quiere analizar. Visualmente cuanto más lejos de la diagonal está la curva, mayor es la desigualdad.

Se requiere el cálculo de las frecuencias relativas acumuladas de los individuos ordenados según la variable bajo estudio, y la frecuencia relativa acumulada de la variable misma.

library(ineq)

db.lorenz <- db %>% 
  # 1)  Ordenar los datos por la variable a analizar de manera ascendente
  arrange(rmm) %>%
  # 2)  Calcular la fr's acumulada de la poblacion y la variable a analizar
  mutate(rmm.fr = cumsum(rmm) / sum(rmm) ,
         pobnv.fr = cumsum(pobnv) / sum(pobnv) )

Para posteriomente graficarlos.

# 3)  Graficar ambas frecuencias relativas
db.lorenz %>%
  ggplot(aes(pobnv.fr, rmm.fr)) +
  geom_path(color  = "darkorange") + 
  geom_point(color = "darkorange") + 
  geom_abline() + # linea de igualdad
  labs(title = " Curva de Lorenz ",
       x = "Proporción acumulada de la poblacion",
       y = "Proporción acumulada del indicador de Salud") +
  theme_bw()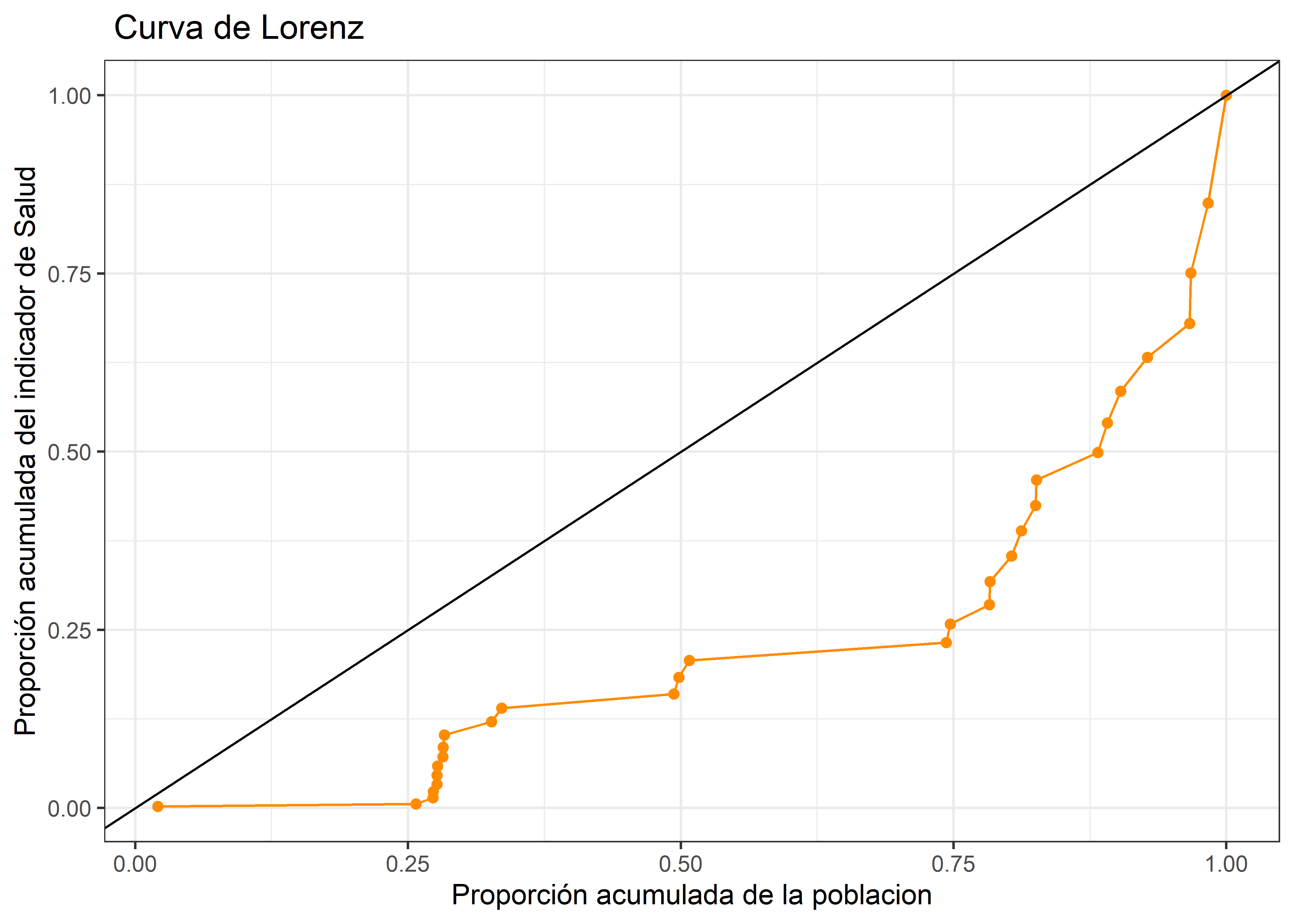

Calculada la curva de lorenz, el coeficiente de gini vendría a ser el área comprendida entre la diagonal de equidad perfecta y la curva de lorenz.

db.lorenz %>%
  ggplot(aes(pobnv.fr, rmm.fr)) +
  geom_path(color  = "darkorange") + 
  geom_point(color = "darkorange") + 
  geom_abline() + # linea de igualdad
  geom_ribbon(aes(ymin = pobnv.fr, ymax = rmm.fr), fill = "darkorange", alpha = 0.3) +
  labs(
    title = " Curva de Lorenz ",
    x = "Proporción acumulada de la poblacion",
    y = "Proporción acumulada del indicador de Salud"
  ) +
  theme_bw()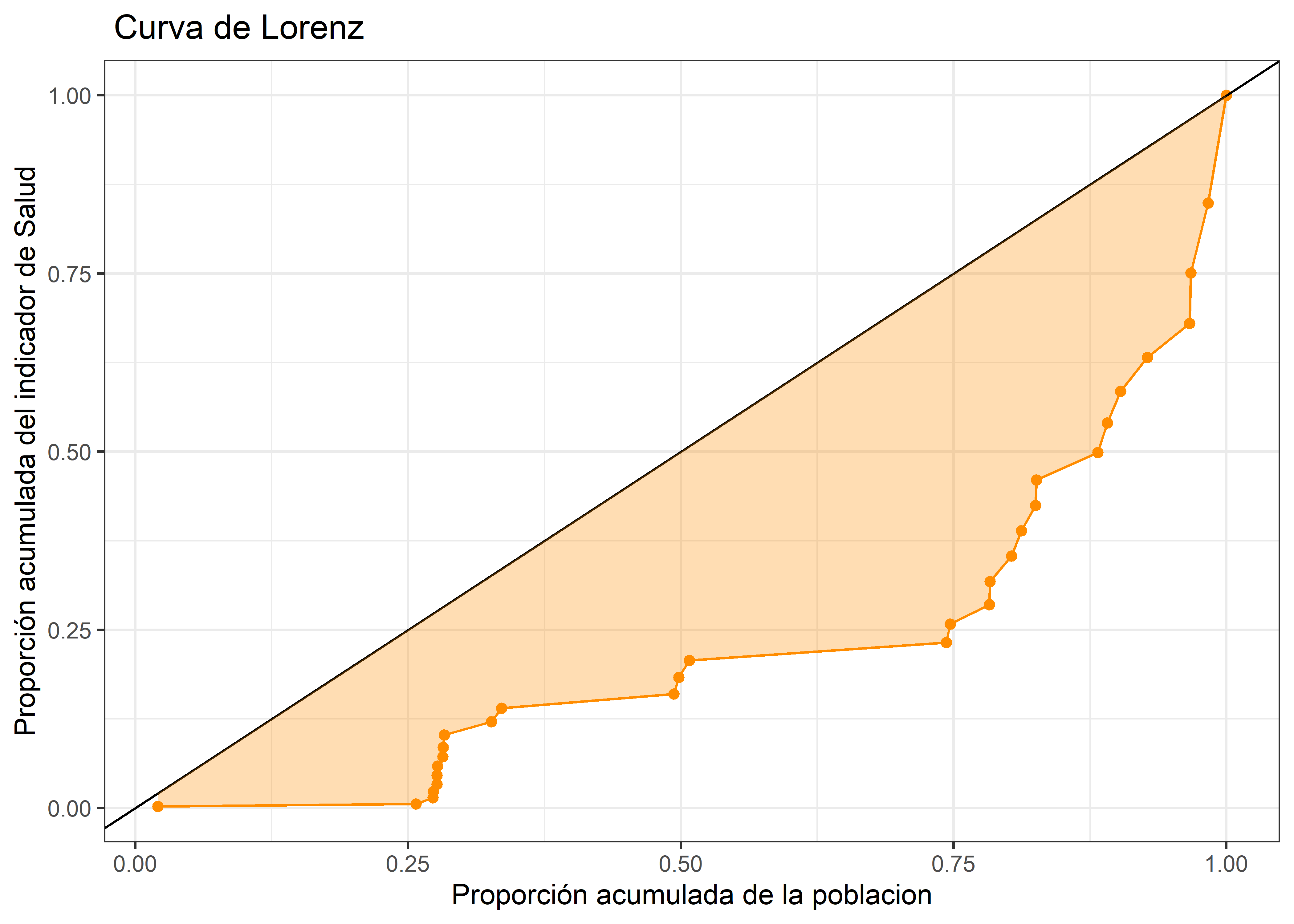

Sin embargo, propiamente su calculo se puede obtener usando la siguiente expresión:

\[ G = \frac{1}{n} ( \frac{2 \sum_{i=1}^{n} i x_i}{\sum_{i=1}^{n} x_i} - (n + 1)) \]

Donde:

  • \(n\) es el número individuos o grupos.

  • \(x_i\) representa el valor del indicador del \(i\) -simo individuo o grupo

gini_coefficient <- function(x) {
  # Ordenamos los datos segun el peor nivel del indicador de salud al mejor 
  x <- sort(x)
  # Indexamos cada registro
  index <- 1:length(x)
  # Calculamos el numero de datos del indicador
  n <- length(x)
  # calculamos el coeficiente de gini  
  return ((sum((2 * index - n  - 1) * x)) / (n * sum(x)))
}

gini_coefficient(db.lorenz$rmm.fr)
[1] 0.4844171

Asimismo, R cuenta con el paquete ineq con el cual podemos facilitar el calculo del índice de Gini y muchos otros más:

Gini(db.lorenz$rmm.fr)
[1] 0.4844171

Este indicador varía entre 0 y 1, correspondiendo el 0 a una distribución perfectamente igualitaria respecto de la variable de bajo analisis, y el 1 a una distribución perfectamente desigual. Así, cuanto mayor sea el índice, mayor será la desigualdad.

Dado lo anterior en el presente caso de estudio, se observo un índice de Gini de 0.4, lo cual da cuenta que la razón de mortalidad materna tiende a estar más concentrada en algunos países, sin embargo un Gini de 0.4 no es extremadamente alto, lo que sugiere que si bien existe desigualdad, no es de la magnitud más extrema posible.

23.3.2 Indice de Theil

El indice de Theil tambien es una medida de desigualdad que se utiliza para evaluar la distribución del indicador. Sin embargo emplea el concepto de la entropía de la información para medir la discrepancia entre los valores observados y los valores promedio. El índice de Theil se calcula mediante la siguiente expresión:

\[ T = \sum_{i=1}^{n} ( \frac{x_i}{\bar{x}}) \cdot \ln ( \frac{x_i}{\bar{x}}) \]

Donde:

  • \(n\) es el número individuos o grupos.

  • \(x_i\) representa el valor del indicador del \(i\) -simo individuo o grupo

theil_index <- function(x) {
  n        <- length(x)
  mean_x   <- mean(x)
  theil    <- sum((x/mean_x) * log(x/mean_x))
  return(theil/n)
}

theil_index(db.lorenz$rmm)
[1] 0.3134856

Esta expresión también puede ser calculada empleando el paquete ineq.

Theil(db.lorenz$rmm)
[1] 0.3134856

Este indicador varía entre 0 y ∞+, correspondiendo el 0 a una distribución perfectamente equitativa respecto de la variable de bajo analisis, y el ∞+ a una distribución perfectamente desigual. Así, cuanto mayor sea el índice, mayor será la desigualdad.

El indice de Theil (0.31) en este caso sugiere que hay una cantidad moderada de desigualdad en los datos, lo que indicaría que no son muchos los paises que tienen una distribución de valores que difiere significativamente de la media poblacional ponderada.

23.3.3 Indice de Atkinson

Es otro indicador para medir la desigualdad, pero a diferencia del Coeficiente de Gini y el Índice de Theil, el Índice de Atkinson toma en cuenta tanto el nivel de desigualdad como la aversión de la sociedad hacia esa desigualdad (Atkinson 1970).

\[ A(\epsilon) = 1 - \frac{1}{\bar{x}} \left( \frac{1}{n} \sum_{i=1}^{n} x_i^{1-\epsilon} \right)^{\frac{1}{1-\epsilon}} \]

Donde:

  • \(n\) es el número individuos o grupos.

  • \(x_i\) representa el valor del indicador del \(i\) -simo individuo o grupo.

  • \(\epsilon\) es el parámetro que refleja la adversión de la sociedad a la desigudad. Mayores valores de \(\epsilon\) indicaran mayor adversión por la desigualdad y viceversa.

atkinson_index <- function(x, epsilon) {
  n <- length(x)
  mean_x   <- mean(x)
  atkinson <- 1 - (1 / mean_x) * ((1 / n) * sum(x^(1 - epsilon)))^(1 / (1 - epsilon))
  return(atkinson)
}

atkinson_index(db.lorenz$rmm,0.5)
[1] 0.1484191

Se puede facilitar el calculo con el paquete ineq.

Atkinson(db.lorenz$rmm,0.5)
[1] 0.1484191

De manera similar al indice de Gini, este indicador varía entre 0 y 1, correspondiendo el 0 a una distribución perfectamente igualitaria respecto de la variable bajo análisis, y 1 a una distribución desigual. Asi dado el anterior cálculo, con un indice de Atkinson de 0.14, se observaría que ante una adversión a la desigualdad moderada \(\epsilon = 0.5\) existiría, en realidad, una desigualdad baja en la razón de mortalidad materna.

23.4 Indicadores de Inequidad (Indicadores de desigualdad relativos a niveles socioeconomicos)

23.4.1 Indice de concentración (IC)

Este indicador, de manera similar al indice de Gini, calcula la desigualdad pero incorporando la dimension socio-económica. Ello lo logra, en principio, al ordenar la variable bajo estudio según el atributo socio-económico. (Wagstaff et al. 2007)

db.eco <- db %>% 
  # 1)  Ordenar los datos por el componente socioeconomico 
  arrange(pdbpc)

Posteriormente, se calculan las frecuencias relativas acumuladas, para generar la Curva de concentración, el homólogo de la Curva de Lorenz.

db.concetracion <- db.eco %>% 
  # 2)  Calcular la frecuencia acumulada de la poblacion y la variable a analizar
  mutate(rmm.fr = cumsum(rmm) / sum(rmm),
         pobnv.fr = cumsum(pobnv) / sum(pobnv))

# 3)  Graficar ambas frecuencias relativas
db.concetracion %>%
  ggplot(aes(pobnv.fr, rmm.fr)) +
  geom_path(color  = "darkorange") + 
  geom_point(color = "darkorange") +
  geom_abline() + # linea de igualdad
  labs(
    title = " Curva de Concentración ",
    x = "Proporción acumulada de la poblacion",
    y = "Proporción acumulada del indicador de Salud"
  ) +
  theme_bw()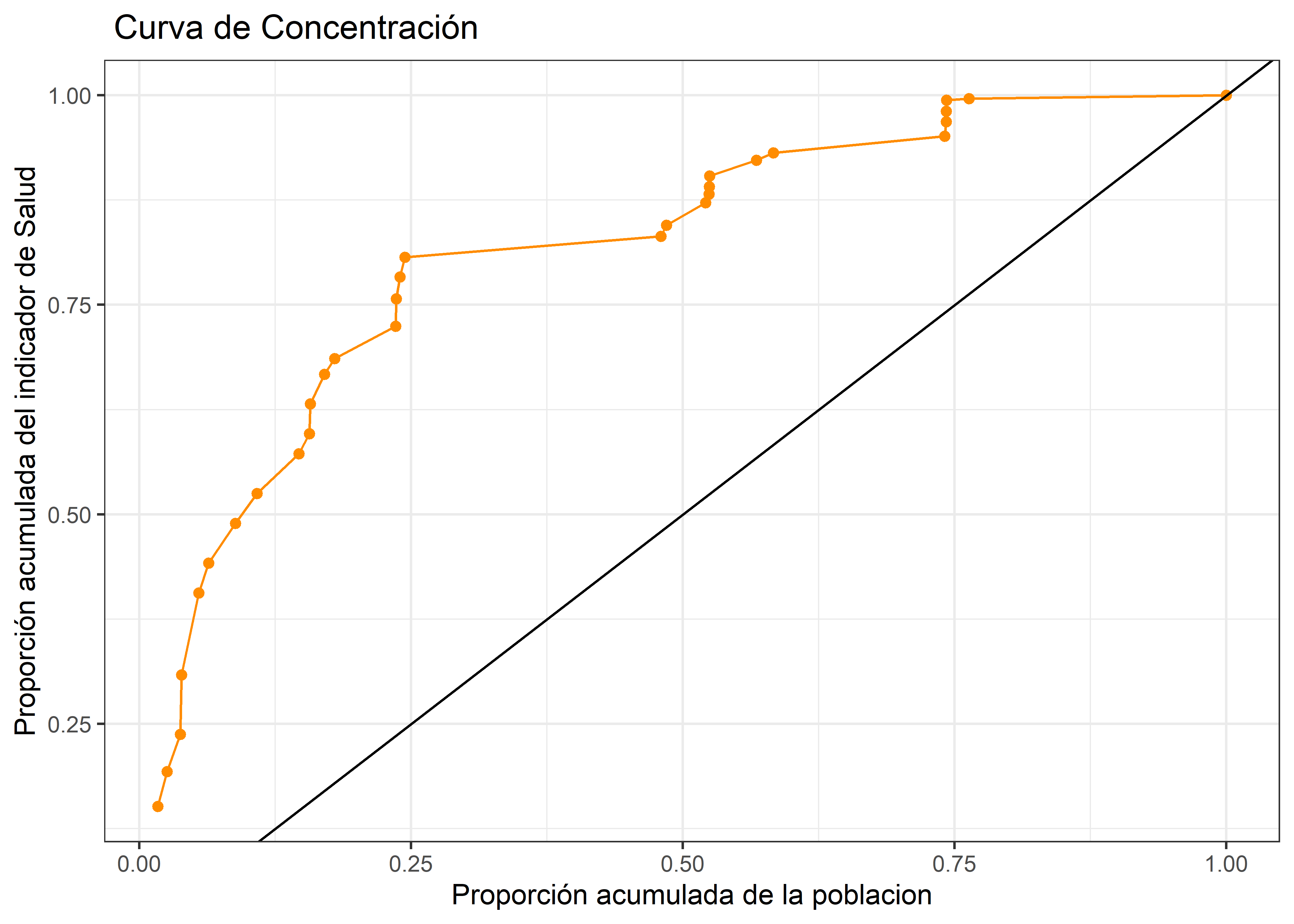

Luego, el índice de concentración sería equivalente al área comprendida entre la curva de concentración y la diagonal de igualdad.

db.concetracion %>%
  ggplot(aes(pobnv.fr, rmm.fr)) +
  geom_path(color  = "darkorange") + 
  geom_point(color = "darkorange") +
  geom_abline() + # linea de igualdad
  geom_ribbon(aes(ymin = pobnv.fr, ymax = rmm.fr), fill = "darkorange", alpha = 0.3) +
  labs(
    title = " Curva de Concentración ",
    x = "Proporción acumulada de la poblacion",
    y = "Proporción acumulada del indicador de Salud"
  ) +
  theme_bw()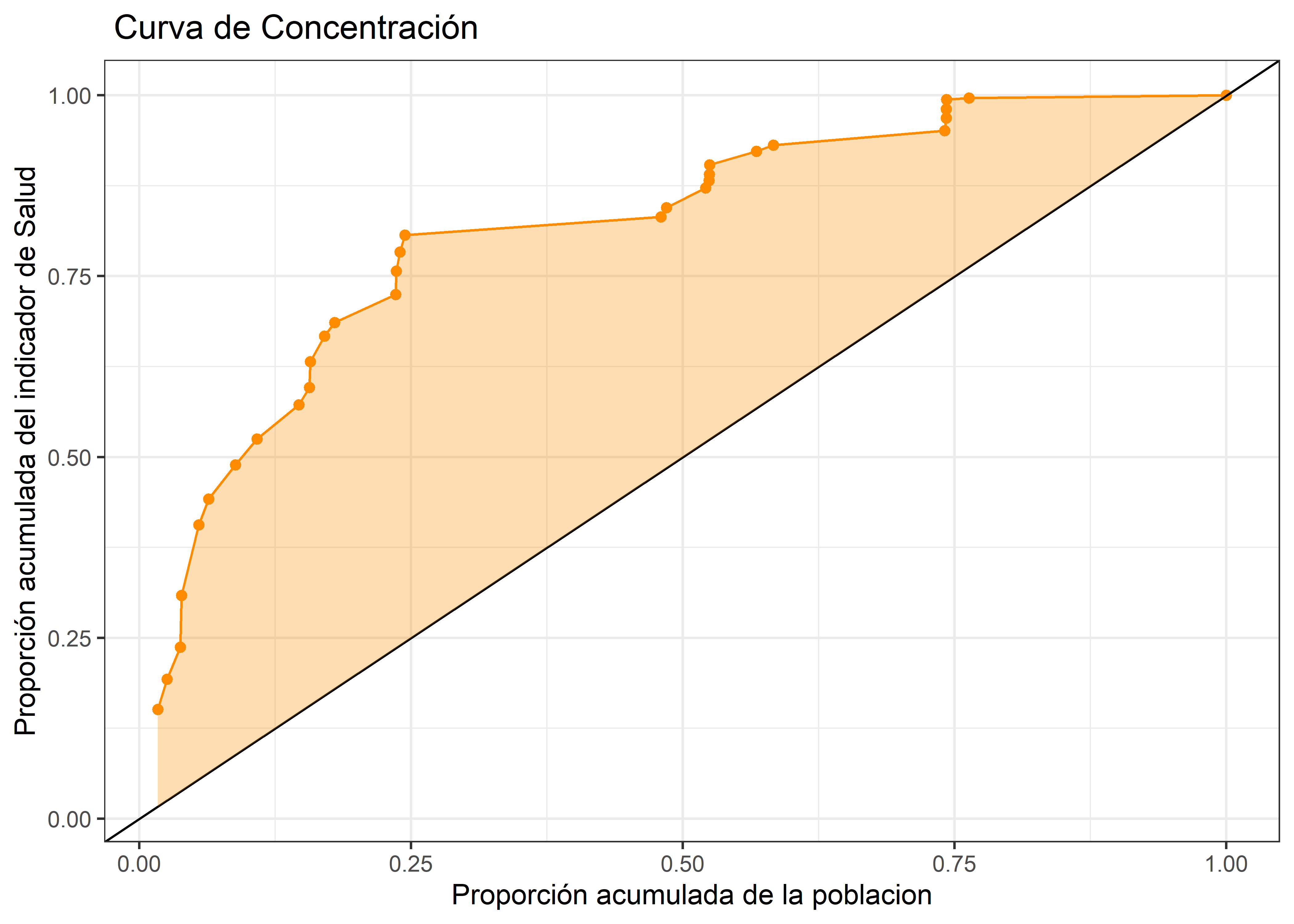

Sin embargo, calcular dicha area deacuerdo a Kakwani(Kakwani y Bank 1980) equivaldría a calcular lo siguiente:

\[ C = \frac{2}{\mu}cov(h,r) \] donde:

  • \(\mu\): Es el promedio de la variable bajo estudio (El atributo asociado a salud)
  • \(h\): La variable bajo estudio
  • \(r\): Frecuencia relativa de la poblacion ordenada segun el atributo socioeconomico
mu <- mean(db.concetracion$rmm)
(CI <- ((2) * cov(db.concetracion$rmm, db.concetracion$pobnv.fr))/mu)
[1] -0.3394782

El índice de concentración tiene un rango de -1 a 1. Un índice de concentración de -1 indica que el atributo bajo estudio está perfectamente concentrado en el grupo con el nivel socio-económico más bajo, mientras que un índice de concentración de 1 indica que la variable está perfectamente concentrada en el grupo con el nivel socioeconomico más alto.

Asi en el caso de estudio, el índice de concentración de desigualdad de -0.33 indicaría que la razón de mortalidad materna está concentrada en los países con el menor PBI percapita. Es decir, los países con la peor situacion económica tienen una razón de mortalidad materna considerablente mayor que aquellos países con mayor PBI percapita.

23.4.2 Indice de pendiente de desigualdad (IPD)

El índice de pendiente de desigualdad (IPD) o SII (por sus siglas en ingles, Slope Index of inequality), es la pendiente de un modelo de regresión, en el cual la variable dependiente o variable objetivo \(Y\) del modelo es el valor del indicador del individuo, grupo o clase; mientras que la independiente \(X\) hace referencia a la posición relativa que ocupan las unidad de análisis, previamente ordenadas según una variable de estratificación socioeconomica (esto es, el gradiente o jerarquía socioeconomica). Esta última variable suele denominarse ridit y es, debido a su definición, una variable comprendida entre 0 (extremo inferior del ordenamiento socioeconómico) y 1 (extremo superior)(Schneider et al. 2005). De este modo, este indice tiene la propiedad de referir las desigualdades de la variable bajo analisis a una dimensión socio-económica.

Dado el planteamiento anterior, el IPD o \(\beta\) asociado al ridit expresa el efecto que tiene sobre una caracteristica (en nuestro caso una asociada a la salud), el desplazarse desde la posición de mayor desventaja social(ridit = 0) a la posición de mayor ventaja social(ridit = 1).

Para su cálculo, ordenamos la base de datos por el indicador socio-económico, de modo tal que el orden sea desde aquellos con menor ventaja socioeconomica a aquellos con la mayor posible.

db.sii <- db %>% 
  arrange(pdbpc)

Calculamos la frecuencia relativa de la poblacion y la acumulamos

db.sii <- db.sii %>% 
  mutate(wpop = pobnv/sum(pobnv),
         Wpop = cumsum(wpop))

Se procede a calcular el ridit

library(zoo)

db.sii <- db.sii %>%  
  mutate(ridit  = ifelse(row_number() == 1, Wpop/2,
                         rollapply(Wpop,width = 2, FUN = sum, fill = NA, 
                                   align = "right")/2) )

Posteriomente, dada la base de datos, planteamos el siguiente modelo de regresion ponderada:

\[WY = \beta_{1} W + \beta_{2} WX\]

En el cual destaca la ausencia del intercepto, debido a que el objetivo es estimar el IPD de manera tal que muestre el cambio en la variable objetivo ( Variable asociada a la Salud), cuando el atributo socioeconomico varie en una unidad desde la peor situacion socioeconomica (ridit = 0), punto de referencia que se veria alterado si se establece un intercepto.

Una vez definido el modelo, calculamos el primer y segundo regresor ponderado; así como la variable objetivo ponderada, en este caso la variable de salud

db.sii.reg <- db.sii  %>% 
  mutate(W  = sqrt(pobnv),
         WX = W * ridit,
         WY = W * rmm)

Finalmente, estimamos el modelo con los regresores y variable objetivo ponderados:

library(broom)

model.sii <- lm(WY ~ WX + W - 1, data = db.sii.reg)
tidy(model.sii)
term estimate std.error statistic p.value
WX -204.6425 34.01947 -6.015451 1.5e-06
W 184.7297 19.56569 9.441512 0.0e+00

Resultado, el cual tambien lo podemos visualizar del siguiente modo:

db.sii.reg.fit <- db.sii.reg %>% 
  # Reescalando
  mutate(fit.values = model.sii$fitted.values/W )

db.sii.reg.fit %>% 
  ggplot() +
  geom_line(aes(x = ridit , y = fit.values), color = "orange") +
  geom_point(aes(x = ridit , y = rmm), shape = 21) +
  geom_text(x = 0.4, y = 200, 
            label = paste("IPD =",round(coef(model.sii)[[1]],2)), 
            color = "orange") +
  labs(x = "Posicion socioeconomica relativa segun pdbpc ",
       y = "Mortalidad materna(x 100 mil nacidos vivos)") +
  theme_bw()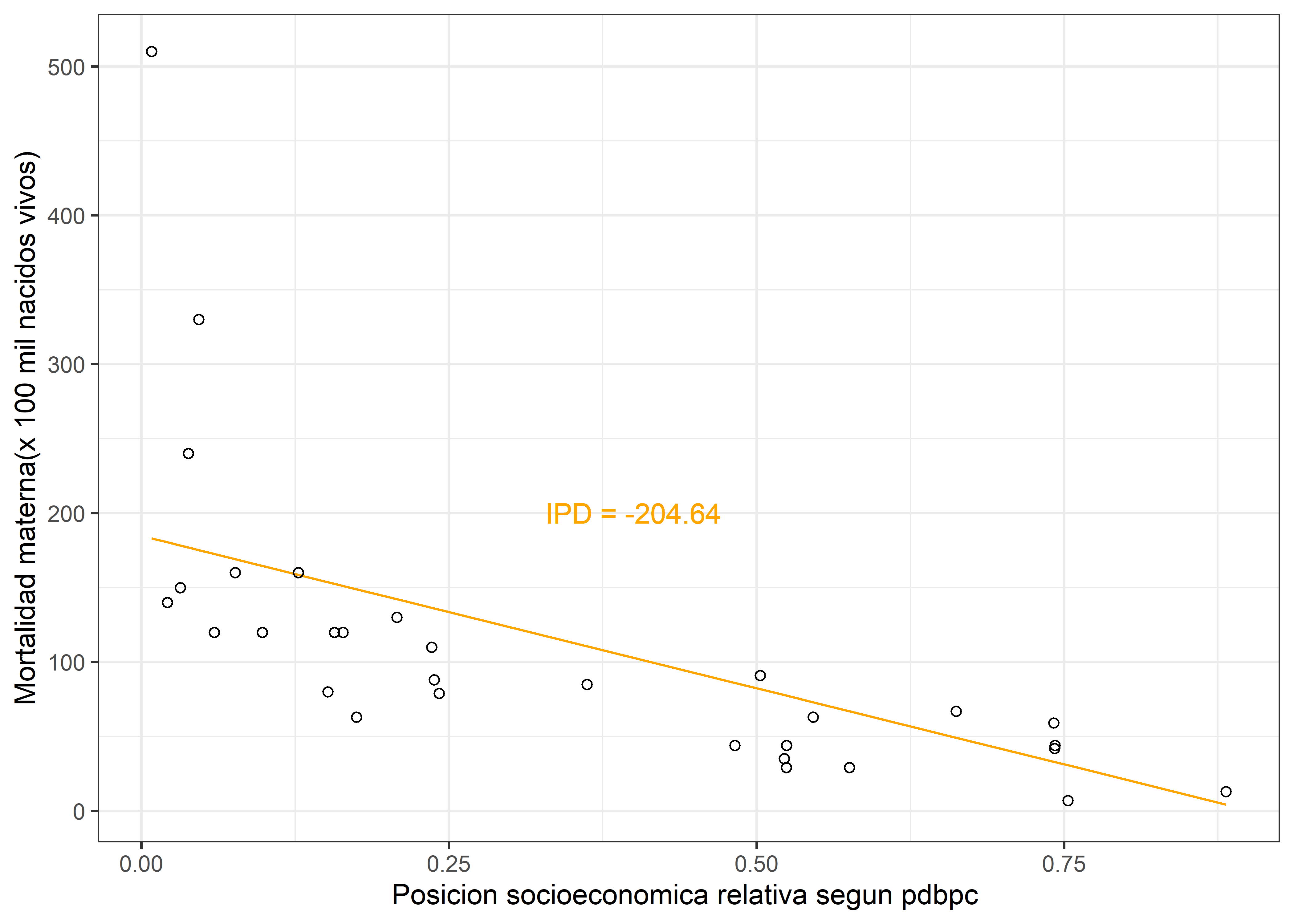

El coeficiente asociado a WX es el valor del indice la pendiente, este indica que habria una tasa de mortalidad de aproximadamente 205 mujeres por cada 100 000 nacidos vivos a traves de la gradiente social (dado el orden que establecimos seria del sector menos aventajado al que más), y ya que la pendiente es negativa, en el presente caso de estudio, una peor situacion economica estaria asociada a un aumento de la tasa mortalidad materna.

23.4.3 Indice relativo de desigualdad (IRD)

Para el cálculo del IRD o RII (Relative index of inequality) deacuerdo a Mackenbach et al. (Mackenbach y Kunst 1997) se establece un cociente entre el IDP (SII) y el valor estimado del indicador asociado a la mejor situacion socioeconomica (mayor valor de ridit)

\[ IRD = \frac{IPD}{\hat{y}_{best}} \]

(RII <- db.sii.reg.fit %>% 
        filter(ridit == max(ridit)) %>% 
        pull(fit.values) %>%   # para emplear expresiones curly-curly
        .[[1]] %>% 
        {coef(model.sii)[[1]] / .} # Calculo RII
 )
[1] -47.42105

El valor así obtenido representa una razón, el atributo del grupo socio-económico más bajo es mayor o menor que la del grupo socioeconómico más alto. Así, en el ejemplo, la razón de mortalidad materna de Haiti (menor nivel socio-económico) se infiere que es aproximadamente 47 veces la de Estados Unidos (mayor nivel socio-económico).

23.5 Otros indicadores de desigualdad

Indicadores de desigualdad Indicadores de Inequidad
Indice de disimilitud (Cowell 2011) Indice de concentración relativa (Kakwani, Wagstaff, y Van Doorslaer 1997)
Medida de kolm (Kolm 1976) Indice de concentración generalizada (Clarke et al. 2002)
Coeficiente Richi-Shutz (Rosenbluth 1951) Indice de Wagstaff (O’Donnell et al. 2016)

Todos los indicadores detallados solo representan los principales de una larga lista que conforman la evolucion de la literatura de indicadores de desigualdad. Al respecto,para profundizar en ello el banco mundial realizo una recopilación de indicadores de desigualdad, asi mismo los paquetes ineq, wINEQ rineq cuentan con funciones para replicar el calculo de muchos otros indicadores.

23.6 Explicacion de la desigualdad: Metodologia Oaxaca-Blinder

Los indicadores antes expuestos proporcionan una medida de la desigualdad, pero no ofrecen detalles sobre las causas o los factores específicos que contribuyen a esa desigualdad. Al respecto, existen metodologías de descomposición como aquella propuesta por Ronald Oaxaca y Alan Blinder, la cual permite lidear con esta tarea.

EL modelo conocido como descomposición de Oaxaca-Blinder permite explicar la diferencia entre 2 poblaciones/muestras de estudio, de modo tal que afirma que la brecha promedio en una determinada variable bajo estudio entre ambas poblaciones se explicaria por:

  • Caracteristicas observables de los dos grupos (componente endowment: los niveles de variables exogenas explicativas).

  • Caracteristicas no observables de los dos grupos (componente coefficient: magnitud de los coeficientes de regresión).

  • La interaccion de ambos componentes (componente interaction) (Oaxaca y Ransom 1994).

Dado lo anterior, para implementar dicha metodología se calculará una variable para clasificar los paises en 2 grupos: bajos ingresos o altos ingresos. Para tal distinción emplearemos la definición de pais de bajos ingresos del banco mundial (Fantom y Serajuddin 2016)

db.oaxaca <- db %>%
  # el umbral del banco mundial para clasificar un pais como de bajos ingresos: $4125 (percapita)
  mutate(alto_ingreso = case_when(
    pdbpc >= 4125 ~ 1,  # altos ingresos
    pdbpc <= 4125 ~ 0,  # bajos ingresos
    FALSE ~ NaN))

Dispuesta asi la agrupación de los paises, podemos observar descriptivamente cual es la diferencia promedio en el atributo objetivo que la metodologia oaxaca-blinder pretender explicar.

db.oaxaca %>% 
  group_by(alto_ingreso) %>% 
  summarise(mean(rmm))
alto_ingreso mean(rmm)
0 248.3333
1 75.2800

Se puede observar que en promedio la diferencia entre ambos grupos es de 173 puntos. Diferencia la cual se explicara al estimar el modelo de oaxaca-blinder empleando para ello el paquete oaxaca (Hlavac 2014).

library(oaxaca)

# estimacion
resultados_oaxaca <- oaxaca(formula = rmm ~ accsani + rtedu + capsalud | alto_ingreso, 
                            # ecuacion oaxaca-blinder
                            data=db.oaxaca,
                            R=100) # numero muestreos bootstrapping

Hecha la estimación del modelo, el objeto resultante de la clase oaxaca contiene el vectoroverall, el cual a su vez dispone de la estimación de la contribución de cada uno de los 3 componentes a la brecha observada entre los 2 grupos antes señalados.

threefold_overall <- resultados_oaxaca$threefold$overall %>%
  enframe(name = "Parametro", value = "valor") %>% # tranfomracion en data.frame
  filter(str_starts(Parametro, "coef")) # selecciona los coeficientes
Resultados descomposicion Threefold Oaxaca-Blinder
Parametro valor
coef(endowments) 85.57098
coef(coefficients) -104.44556
coef(interaction) 191.92792

Así se observa que las variables observadas explican 85.5 puntos de la diferencia promedio entre paises de bajos ingresos y altos ingresos, mientras que aquellas relacionadas con parte no observada (coefficients e interaction) explica 87.5 puntos (191 puntos - 104 puntos) de dicha variación. Es decir, un poco menos de la mitad de las diferencias en el promedio de la razon de muertes maternas estaría explicada por la inversión en capital en salud , la educación, o el acceso a saneamiento mientras que más de la mitad de la diferencias entre paises de bajos y altos ingresos devendria de factores no observados.