17 Medidas de asociación
17.1 Paquetes y data
Los paquetes que se utilizarán son:
La base de datos se deriva del Estudio de Framingham, un estudio de cohorte observacional basado en la población, iniciada en 1948 en Framingham, Massachusetts, EE.UU., cuyo objetivo es identificar los factores de riesgo cardiovascular.
Las variables de interés para el capítulo son las siguientes,
- Condición de angina de pecho al basal:
PREVAP - Condición de Stroke al basal:
PREVSTRK - Condición de Fumador:
CURSMOKE - Casos Incidentes de Hipertensión Arterial:
HYPERTEN - Tiempo hasta desarrollar hipertensión:
TIMEHYP - Sexo del individuo:
SEX - Condición de diabetes:
DIABETES
framingham <- read_csv("./data/framingham_freq_final.csv")17.2 Tabla de contingencia
Los cálculos de Odds Ratio (OR), Relative Risk (RR) y Prevalence Ratio (PR) son herramientas fundamentales en epidemiología para evaluar la asociación entre la exposición a un factor determinado y el resultado. Estos cálculos se fundamentan en una tabla de contingencia que clasifica los resultados según la exposición al factor de interés y el desarrollo de la enfermedad. A continuación se visualiza una tabla cruzada de una población definida por la exposición y el desarrollo de la enfermedad.
| Outcome + | Outcome - | Total | |
|---|---|---|---|
| Expose + | a | b | a + b |
| Expose - | c | d | c + d |
| Total | a + c | b + d | a + b + c + d |
| 1 | Prevalence Ratio (PR) | ||
| 2 | Odds Ratio (OR) | ||
| 3 | Relative Risk (RR) |
17.3 Razón de Prevalencias
La razón de prevalencias (RP) es una medida de asociación que se puede calcular en estudios de diseño transversal. Se calcula dividiendo la prevalencia de la enfermedad en los expuestos (P1) entre la prevalencia de la enfermedad en los no expuestos (P0).
framingham), calcularemos la RP de angina de pecho (PREVAP) al basal (TIME==0) de acuerdo al sexo (SEX).
Calculando la razón de prevalencias con epi.2by2
Para este ejercicio se utilizará la función epi.2by2 del paquete epiR para estimar la razón de prevalencia de angina de pecho al basal.
Es importante mencionar que para el uso adecuado de la función epi.2by2, se debe ingresar un objeto de tipo tabla table como primer argumento. De lo contrario, no se obtendrá ningún resultado. Adicionalmente, se deben factorizar las variables para que puedan ser ingresadas en el orden correcto y epi.2by2 pueda entender los grupos tanto de expuestos como de enfermos.
Al momento de factorizar las dos variables que construirán la tabla de contigencia, se debe considerar que la primera categoría será interpretada por la función epi.2by2 como el grupo de expuestos (SEX = male) o enfermos (PREVAP = Sí).
A continuación, se procederá a crear el objeto tab_angina_sex que contendrá los conteos de ambas variables.
tab_angina_sex <- table(framingham_2$SEX, framingham_2$PREVAP)
tab_angina_sex
Sí No
male 92 1852
female 55 2435Donde:
- Male: Grupo de expuestos
- Female: Grupo de no expuestos o de referencia
- Sí: Grupo de enfermos o que presenta el evento de interés
- No: Grupo de no enfermos o que no presenta el evento de interés
Nota: Es importante tener presente la estructura de la tabla para identificar los grupos y realizar adecuadamente las interpretaciones.
Con la tabla obtenida calcularemos la RP, especificando el diseño del estudio en el argumento method de la función epi.2by2.
Dado que se desea calcular una RP, el argumento method debe especificar que estamos frente a un estudio de diseño transversal (method = cross.sectional). De lo contrario, la función calculará otra medida epidemiológica.
Sabemos que el estudio de Framingham es originalmente una cohorte. Sin embargo, al calcular la RP de angina de pecho al basal, estamos simulando un estudio transversal, ya que solo utilizamos los registros en el tiempo 0, sin posterior seguimiento. Por lo tanto, es correcto estimar esta medida epidemiológica ajustando el parámetro method a cross.sectional.
epi.2by2(tab_angina_sex, method = "cross.sectional") Outcome + Outcome - Total Prev risk *
Exposed + 92 1852 1944 4.73 (3.83 to 5.77)
Exposed - 55 2435 2490 2.21 (1.67 to 2.87)
Total 147 4287 4434 3.32 (2.81 to 3.89)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Prev risk ratio 2.14 (1.54, 2.98)
Prev odds ratio 2.20 (1.57, 3.09)
Attrib prev in the exposed * 2.52 (1.42, 3.63)
Attrib fraction in the exposed (%) 53.33 (35.16, 66.40)
Attrib prev in the population * 1.11 (0.32, 1.89)
Attrib fraction in the population (%) 33.37 (18.13, 45.78)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 21.691 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
Wald confidence limits
CI: confidence interval
* Outcomes per 100 population units Interpretación de la razón de prevalencia
En la población de Framingham, la prevalencia de angina de pecho al basal en hombres es 2.14 (IC 95%: 1.54 - 2.98) veces la prevalencia de angina de pecho al basal en las hombres.
Como podemos observar en la salida de la tabla de contingencia, el intervalo de confianza asociado a la razón de prevalencias no contiene a la unidad (1.00), por lo que podemos afirmar que la razón es estadísticamente significativa.
Adicionalmente, la función epi.2by2 también puede interpretar el resultado de la medida epidemiológica si es que ajustamos el argumento interpret a true.
epi.2by2(tab_angina_sex, method = "cross.sectional", interpret = TRUE) Outcome + Outcome - Total Prev risk *
Exposed + 92 1852 1944 4.73 (3.83 to 5.77)
Exposed - 55 2435 2490 2.21 (1.67 to 2.87)
Total 147 4287 4434 3.32 (2.81 to 3.89)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Prev risk ratio 2.14 (1.54, 2.98)
Prev odds ratio 2.20 (1.57, 3.09)
Attrib prev in the exposed * 2.52 (1.42, 3.63)
Attrib fraction in the exposed (%) 53.33 (35.16, 66.40)
Attrib prev in the population * 1.11 (0.32, 1.89)
Attrib fraction in the population (%) 33.37 (18.13, 45.78)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 21.691 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
Wald confidence limits
CI: confidence interval
* Outcomes per 100 population units
Measures of association strength:
The outcome prevalence risk among the exposed was 2.14 (95% CI 1.54 to 2.98) times greater than the outcome prevalence risk among the unexposed.
The outcome prevalence odds among the exposed was 2.2 (95% CI 1.57 to 3.09) times greater than the outcome prevalence odds among the unexposed.
Measures of effect in the exposed:
Exposure changed the outcome prevalence risk in the exposed by 2.71 (95% CI 1.53 to 3.89) per 100 population units. 54.5% of outcomes in the exposed were attributable to exposure (95% CI 35.8% to 68.1%).
Number needed to treat for benefit (NNTB) and harm (NNTH):
The number needed to treat for one subject to benefit (NNTB) is 40 (95% CI 28 to 71).
Measures of effect in the population:
Exposure changed the outcome prevalence risk in the population by 1.17 (95% CI 0.36 to 1.98) per 100 population units. 34.1% of outcomes in the population were attributable to exposure (95% CI 27.1% to 41.3%). NOTA: En caso se desee modificar la categoría de referencia, se deberá factorizar la variable y colocar la nueva categoría de referencia como segundo nivel.
El objeto framingham_3 ya contiene la nueva variable factorizada con el nivel “male” como categoría de referencia. Ahora se creará la tabla con dicha modificación.
tab_angina_sex_2 <- table(framingham_3$SEX, framingham_3$PREVAP)
tab_angina_sex_2
Sí No
female 55 2435
male 92 1852Es importante recordar que epi.2by2() entiende a la primera fila de la tabla como el grupo expuesto. De acuerdo a los resultados del objeto table_prevalence_2, nuestra categoría de referencia es female.
epi.2by2(tab_angina_sex_2, method = "cross.sectional") Outcome + Outcome - Total Prev risk *
Exposed + 55 2435 2490 2.21 (1.67 to 2.87)
Exposed - 92 1852 1944 4.73 (3.83 to 5.77)
Total 147 4287 4434 3.32 (2.81 to 3.89)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Prev risk ratio 0.47 (0.34, 0.65)
Prev odds ratio 0.45 (0.32, 0.64)
Attrib prev in the exposed * -2.52 (-3.63, -1.42)
Attrib fraction in the exposed (%) -114.25 (-197.65, -54.22)
Attrib prev in the population * -1.42 (-2.50, -0.34)
Attrib fraction in the population (%) -42.75 (-61.51, -26.16)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 21.691 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
Wald confidence limits
CI: confidence interval
* Outcomes per 100 population units Calculando la razón de prevalencia con contingency
La función epi.2by2() requiere de una ligera modificación al objeto que entrará como primer argumento para realizar los cálculos, es decir, este tiene que ser específicamente una tabla. Con la función contingency() del paquete pubh se puede calcular la medida epidemiológica directamente desde la base de datos. Sin embargo, es importante conocer que al momento de la factorización, contingency considera al segundo nivel de las variables como los grupos expuestos y enfermos.
framingham_2 %>%
mutate(PREVAP = fct_rev(PREVAP),
SEX = fct_rev(SEX)) %>%
contingency(PREVAP ~ SEX, method = "cross.sectional") Outcome
Predictor Sí No
male 92 1852
female 55 2435
Outcome + Outcome - Total Prev risk *
Exposed + 92 1852 1944 4.73 (3.83 to 5.77)
Exposed - 55 2435 2490 2.21 (1.67 to 2.87)
Total 147 4287 4434 3.32 (2.81 to 3.89)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Prev risk ratio 2.14 (1.54, 2.98)
Prev odds ratio 2.20 (1.57, 3.09)
Attrib prev in the exposed * 2.52 (1.42, 3.63)
Attrib fraction in the exposed (%) 53.33 (35.16, 66.40)
Attrib prev in the population * 1.11 (0.32, 1.89)
Attrib fraction in the population (%) 33.37 (18.13, 45.78)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 21.691 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
Wald confidence limits
CI: confidence interval
* Outcomes per 100 population units
Pearson's Chi-squared test with Yates' continuity correction
data: dat
X-squared = 20.911, df = 1, p-value = 4.811e-0617.4 Razón de Odds
La razón de Odds u Odds ratio (OR) indica si distintos grupos de exposición tienen distintos odds de ocurrencia de un evento.
Utilizando la base de datos del estudio de Framingham, calcularemos el OR de stroke prevalente (PREVSTRK) al basal (TIME==0) de acuerdo a la condición de fumador (CURSMOKE) usando epi.2by2 y contingency.
Calculando el Odds Ratio con epi.2by2
Procedemos a crear la tabla 2x2 para calcular posteriormente el OR.
stroke_table <- table(stroke_data$CURSMOKE, stroke_data$PREVSTRK)
stroke_table
Stroke Prevalente Sin Stroke
Fumador 12 2169
No Fumador 20 2233Finalmente, calcularemos el OR con el objeto stroke_table ajustando el argumento method de la función epi.2by2 a case.control.
epi.2by2(stroke_table, method = "case.control") Outcome + Outcome - Total Odds
Exposed + 12 2169 2181 0.01 (0.00 to 0.01)
Exposed - 20 2233 2253 0.01 (0.01 to 0.01)
Total 32 4402 4434 0.01 (0.00 to 0.01)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Exposure odds ratio 0.62 (0.30, 1.27)
Attrib fraction (est) in the exposed (%) -61.87 (-264.12, 24.85)
Attrib fraction (est) in the population (%) -23.21 (-61.39, 5.94)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 1.762 Pr>chi2 = 0.184
Fisher exact test that OR = 1: Pr>chi2 = 0.216
Wald confidence limits
CI: confidence intervalInterpretación:
En la población de Framingham, los odds de stroke en el grupo de fumadores es 0.62 (IC 95%: 0.30 - 1.27) veces los odds de stroke en el grupo de no fumadores. Este resultado no es estadísticamente significativo, pues el intervalo de confianza contiene a la unidad (1.00).
Calculando el Odds Ratio con contingency
stroke_data %>%
mutate(PREVSTRK = fct_rev(PREVSTRK),
CURSMOKE = fct_rev(CURSMOKE)) %>%
contingency(PREVSTRK ~ CURSMOKE, method = "case.control") Outcome
Predictor Stroke Prevalente Sin Stroke
Fumador 12 2169
No Fumador 20 2233
Outcome + Outcome - Total Odds
Exposed + 12 2169 2181 0.01 (0.00 to 0.01)
Exposed - 20 2233 2253 0.01 (0.01 to 0.01)
Total 32 4402 4434 0.01 (0.00 to 0.01)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Exposure odds ratio 0.62 (0.30, 1.27)
Attrib fraction (est) in the exposed (%) -61.87 (-264.12, 24.85)
Attrib fraction (est) in the population (%) -23.21 (-61.39, 5.94)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 1.762 Pr>chi2 = 0.184
Fisher exact test that OR = 1: Pr>chi2 = 0.216
Wald confidence limits
CI: confidence interval
Pearson's Chi-squared test with Yates' continuity correction
data: dat
X-squared = 1.3222, df = 1, p-value = 0.250217.5 Razón de incidencias acumuladas
La razón de los riesgos (o de las tasas de incidencia) se puede definir como la probabilidad de que un evento (el desarrollo de una enfermedad) se produzca en personas expuestas en comparación con la probabilidad del evento en personas no expuestas, o como el cociente de estas dos probabilidades. En un estudio de cohortes, el riesgo relativo puede calcularse directamente.
Para este ejercicio, seguiremos utilizando la base del estudio de Framingham framingham, pero esta vez nos enfocaremos en los casos incidentes de hipertensión arterial (HYPERTEN) para el periodo 3 del estudio (PERIOD == 3). Calcularemos el riesgo de hipertensión arterial por condición de diabetes (DIABETES).
Nota: Recordemos que cuando hablamos de incidencia, nos estamos refiriendo a todos los casos nuevos. Por tal motivo, debemos eliminar a todos aquellos sujetos que hayan sido positivos al basal.
Calculando la razón de incidencias con epi.2by2
Una vez que los individuos con hipertensión prevalente han sido retirados, se creará la tabla que ingresará a la función epi.2by2. Pero antes, se deberá factorizar las variables correctamente para obtener el cálculo adecuado.
Luego de factorizar en el orden correcto los niveles de las variables, se podrá crear la tabla para el cálculo de la razón de incidencias.
tab_incience <- table(incident_hyperten$DIABETES, incident_hyperten$HYPERTEN)
tab_incience
Hipertension Incidente Sin Hipertension
Diabetico 24 28
No diabetico 477 781Una vez que hemos obtenido la tabla de contingencia, procederemos a calcular el RR, configurando el argumento method a cohort.count.
epi.2by2(tab_incience, method = "cohort.count") Outcome + Outcome - Total Inc risk *
Exposed + 24 28 52 46.15 (32.23 to 60.53)
Exposed - 477 781 1258 37.92 (35.23 to 40.66)
Total 501 809 1310 38.24 (35.60 to 40.94)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Inc risk ratio 1.22 (0.90, 1.65)
Inc odds ratio 1.40 (0.80, 2.45)
Attrib risk in the exposed * 8.24 (-5.58, 22.05)
Attrib fraction in the exposed (%) 17.85 (-11.12, 39.26)
Attrib risk in the population * 0.33 (-3.43, 4.08)
Attrib fraction in the population (%) 0.85 (-0.61, 2.30)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 1.434 Pr>chi2 = 0.231
Fisher exact test that OR = 1: Pr>chi2 = 0.246
Wald confidence limits
CI: confidence interval
* Outcomes per 100 population units Interpretación
En la población de Framingham, el riesgo de hipertensión arterial en el grupo de diabéticos es 1.22 (IC 95%: 0.90 - 1.65) veces el riesgo de hipertensión arterial en el grupo de los no diabéticos.
Como se puede observar en la salida de la tabla de contingencia, el intervalo de confianza contiene a la unidad (1.00), es decir, la asociación no es estadísticamente significativa.
Calculando la razón de incidencias con contingency
incident_hyperten %>%
mutate(HYPERTEN = fct_rev(HYPERTEN),
DIABETES = fct_rev(DIABETES)) %>%
contingency(HYPERTEN ~ DIABETES, method = "cohort.count") Outcome
Predictor Hipertension Incidente Sin Hipertension
Diabetico 24 28
No diabetico 477 781
Outcome + Outcome - Total Inc risk *
Exposed + 24 28 52 46.15 (32.23 to 60.53)
Exposed - 477 781 1258 37.92 (35.23 to 40.66)
Total 501 809 1310 38.24 (35.60 to 40.94)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Inc risk ratio 1.22 (0.90, 1.65)
Inc odds ratio 1.40 (0.80, 2.45)
Attrib risk in the exposed * 8.24 (-5.58, 22.05)
Attrib fraction in the exposed (%) 17.85 (-11.12, 39.26)
Attrib risk in the population * 0.33 (-3.43, 4.08)
Attrib fraction in the population (%) 0.85 (-0.61, 2.30)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 1.434 Pr>chi2 = 0.231
Fisher exact test that OR = 1: Pr>chi2 = 0.246
Wald confidence limits
CI: confidence interval
* Outcomes per 100 population units
Pearson's Chi-squared test with Yates' continuity correction
data: dat
X-squared = 1.1068, df = 1, p-value = 0.292817.6 Razón de tasas de incidencia
En epidemiología, los cálculos de Razón de Tasa de Incidencia (RTI) son esenciales para evaluar cómo la exposición a un factor puede influir en la incidencia de una enfermedad en una población. La tabla a continuación muestra una representación de la relación entre la exposición (expuestos y no expuestos) y el tiempo-persona, que es una medida de la cantidad de tiempo durante el cual cada individuo está expuesto a un riesgo de desarrollar la enfermedad de interés.
| Outcome + | Tiempo-persona | |
|---|---|---|
| Expose + | a | b |
| Expose - | c | d |
| 1 | Razón de taza de incidencia (RTI) |
Las RTI también son llamadas como razón de densidad de incidencia (RDI) y pueden ser resumidas en la siguiente ecuación,
Para este ejercicio, se estimará la razón de tasas de incidencia de hipertensión arterial (HYPERTEN) según la condición de diabetes (DIABETES) durante el periodo 3 (PERIOD==3) del estudio.
Se utilizará el objeto incident_hyperten, el cual ya contiene a todos los individuos libres de hipertensión y que forman parte del periodo 3. Al ser una razón de tasas de incidencia, solo importan los casos. Por tal motivo se aplicará ese filtro antes de realizar el conteo de casos y la suma de tiempos de seguimientos estratificados por la condición de diabetes.
rti_data <- incident_hyperten %>%
filter(HYPERTEN == "Hipertension Incidente") %>%
group_by(DIABETES) %>%
summarise(cases = n(),
personas_tiempo = sum(TIMEHYP, na.rm = T)
) %>%
column_to_rownames("DIABETES")
rti_data cases personas_tiempo
Diabetico 24 154783
No diabetico 477 3132359El objeto rti_data tiene que ser convertido a matriz para que pueda ser utilizado en la función epi.2by2.
matrix_data <- as.matrix(rti_data)Finalmente, se procederá a ejecutar el cálculo de la razón de tasas de incidencias.
epi.2by2(matrix_data, method = "cohort.time", units = 100) Outcome + Time at risk Inc rate *
Exposed + 24 154783 0.02 (0.01 to 0.02)
Exposed - 477 3132359 0.02 (0.01 to 0.02)
Total 501 3287142 0.02 (0.01 to 0.02)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Inc rate ratio 1.02 (0.65, 1.53)
Attrib rate in the exposed * 0.00 (-0.01, 0.01)
Attrib fraction in the exposed (%) 1.79 (-54.82, 34.79)
Attrib rate in the population * 0.00 (-0.00, 0.00)
Attrib fraction in the population (%) 0.09 (-0.13, 0.31)
-------------------------------------------------------------------
Wald confidence limits
CI: confidence interval
* Outcomes per 100 units of population time at risk Interpretación:
En la población de Framingham, la tasa de incidencia de hipertensión arterial en el grupo de diabéticos es 1.02 (IC 95%: 0.65 - 1.53) veces la tasa de incidencia de hipertensión arterial en el grupo de no diabéticos.
Otra forma de poder calcular la razón de tasas de incidencias utilizando el objeto rti_data es a través de la función contingency2, la cual permite ingresar los valores de cada uno de nuestros grupos.
La sintaxis de la función sería la siguiente,
contingency2(a, b, c, d, method = "")Donde,
- a: Número de casos donde la exposición y el outcome están presentes
- b: Número de casos donde la exposición está presente y el outcome está ausente
- c: Número de casos donde la exposición está ausente y el outcome está presente
- d: Número de casos donde la exposición y el outcome están ausentes
- method: Diseño de estudio a tener presente para el cálculo
En este caso, ya que estamos frente a un cálculo de razón de tasas de incidencias, los argumentos serían los siguientes,
- a: Casos expuestos cuando el outcome está presente
- b: Tiempo de seguimiento para a
- c: Casos no expuestos cuando el outcome está presente
- d: Tiempo de seguimiento para c
- method: cohort.time
rti_data cases personas_tiempo
Diabetico 24 154783
No diabetico 477 3132359contingency2(24, 154783, 477, 3132359, method = "cohort.time")
Yes No
Yes 24 154783
No 477 3132359
Outcome + Time at risk Inc rate *
Exposed + 24 154783 0.02 (0.01 to 0.02)
Exposed - 477 3132359 0.02 (0.01 to 0.02)
Total 501 3287142 0.02 (0.01 to 0.02)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Inc rate ratio 1.02 (0.65, 1.53)
Attrib rate in the exposed * 0.00 (-0.01, 0.01)
Attrib fraction in the exposed (%) 1.79 (-54.82, 34.79)
Attrib rate in the population * 0.00 (-0.00, 0.00)
Attrib fraction in the population (%) 0.09 (-0.13, 0.31)
-------------------------------------------------------------------
Wald confidence limits
CI: confidence interval
* Outcomes per 100 units of population time at risk
Pearson's Chi-squared test with Yates' continuity correction
data: dat
X-squared = 2.6257e-25, df = 1, p-value = 1NOTA GENERAL: Hasta el momento solo se están calculando medidas de asociación crudas, es decir, la relación entre el evento y la exposición no está siendo ajustada por el efecto confusor de otras variables. En los capítulos de diseño de estudios se aprenderá a controlar por confusión utilizando modelos lineales generalizados.
17.7 Odds ratio y Riesgo Relativo
El Odds Ratio (OR) y el Riesgo Relativo (RR) pueden ser similares en situaciones en las que la enfermedad o el resultado de interés son poco frecuentes en la población en general. Cuando la incidencia de la enfermedad o evento en la población no expuesta es baja (<10%), es posible que el OR y el RR produzcan estimaciones numéricamente cercanas. Cuando la suposición de enfermedad rara no se cumple, el OR no ajustado sobrestima el RR.
Si la incidencia de la enfermedad en el grupo de no expuestos es 25%, en los siguientes ejemplos observaremos cómo los valores del OR varían según el incremento del RR.
17.7.1 Caso 1: RR=1
En un estudio de cohortes se determinó que la incidencia del evento en pacientes expuestos y no expuestos a una sustancia X fue igual al 25%, considerando un tamaño de muestra de 2000 sujetos, tendremos la siguiente tabla 2x2.
tab_equal <- as.table(rbind(c(250,750), c(250,750)))
dimnames(tab_equal) <- list( c("Expuestos", "No expuestos"),
c("Evento", "No evento"))
tab_equal Evento No evento
Expuestos 250 750
No expuestos 250 750Dado esto podemos realizar el cálculo del OR y RR usando el comando epi.2by2
caso_01 <- epi.2by2(dat = tab_equal, method = "cohort.count")
caso_01 Outcome + Outcome - Total Inc risk *
Exposed + 250 750 1000 25.00 (22.34 to 27.81)
Exposed - 250 750 1000 25.00 (22.34 to 27.81)
Total 500 1500 2000 25.00 (23.12 to 26.96)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Inc risk ratio 1.00 (0.86, 1.16)
Inc odds ratio 1.00 (0.82, 1.22)
Attrib risk in the exposed * 0.00 (-3.80, 3.80)
Attrib fraction in the exposed (%) 0.00 (-16.39, 14.09)
Attrib risk in the population * 0.00 (-3.29, 3.29)
Attrib fraction in the population (%) 0.00 (-7.89, 7.31)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 0.000 Pr>chi2 = 1.000
Fisher exact test that OR = 1: Pr>chi2 = 1.000
Wald confidence limits
CI: confidence interval
* Outcomes per 100 population units De acuerdo a la salida del epi.2by2, comprobamos que para incidencias iguales en el grupo de expuestos y no expuestos, el RR y el OR son iguales a 1.
17.7.2 Caso 2: RR=2
Supongamos que la frecuencia del evento en los expuestos incrementó a 500, manteniéndose la frecuencia del evento en los no expuestos. Entonces tendremos la siguiente tabla 2x2:
tab_dif1 <- as.table(rbind(c(500,500), c(250,750)))
dimnames(tab_dif1) <- list( c("Expuestos", "No expuestos"),
c("Evento ocurre", "Evento no ocurre"))
tab_dif1 Evento ocurre Evento no ocurre
Expuestos 500 500
No expuestos 250 750Realicemos el cálculo del OR y RR para este caso:
caso_02 <- epi.2by2(dat = tab_dif1, method = "cohort.count")
caso_02 Outcome + Outcome - Total Inc risk *
Exposed + 500 500 1000 50.00 (46.85 to 53.15)
Exposed - 250 750 1000 25.00 (22.34 to 27.81)
Total 750 1250 2000 37.50 (35.37 to 39.66)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Inc risk ratio 2.00 (1.77, 2.26)
Inc odds ratio 3.00 (2.48, 3.63)
Attrib risk in the exposed * 25.00 (20.90, 29.10)
Attrib fraction in the exposed (%) 50.00 (43.40, 55.83)
Attrib risk in the population * 12.50 (9.08, 15.92)
Attrib fraction in the population (%) 33.33 (27.50, 38.70)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 133.333 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
Wald confidence limits
CI: confidence interval
* Outcomes per 100 population units Podemos observar que para un RR de 2, el OR incrementa a 3. Es decir, el OR sobrestimaría al RR en el caso en que se aumente en una unidad el RR, cuando mantenemos la Incidencia de no expuestos constantes.
17.7.3 Caso 3: RR=3
Ahora evaluemos la diferencia de los estimados cuando la frecuencia del evento en los expuestos incrementa a 750, manteniéndose la frecuencia del evento en los no expuestos. Tendremos la siguiente tabla 2x2:
tab_dif2 <- as.table(rbind(c(750,250), c(250,750)))
dimnames(tab_dif2) <- list( c("Expuestos", "No expuestos"),
c("Evento ocurre", "Evento no ocurre"))
tab_dif2 Evento ocurre Evento no ocurre
Expuestos 750 250
No expuestos 250 750Realicemos el cálculo del OR y RR para este caso:
caso_03 <- epi.2by2(dat = tab_dif2, method = "cohort.count")
caso_03 Outcome + Outcome - Total Inc risk *
Exposed + 750 250 1000 75.00 (72.19 to 77.66)
Exposed - 250 750 1000 25.00 (22.34 to 27.81)
Total 1000 1000 2000 50.00 (47.79 to 52.21)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Inc risk ratio 3.00 (2.68, 3.36)
Inc odds ratio 9.00 (7.35, 11.02)
Attrib risk in the exposed * 50.00 (46.20, 53.80)
Attrib fraction in the exposed (%) 66.67 (62.67, 70.23)
Attrib risk in the population * 25.00 (21.54, 28.46)
Attrib fraction in the population (%) 50.00 (45.42, 54.20)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 500.000 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
Wald confidence limits
CI: confidence interval
* Outcomes per 100 population units Podemos ver que al variar la incidencia de los casos en el grupo de expuestos, el OR sobrestima en mayor medida al RR.
En general podemos decir que, cuando la incidencia del evento en el grupo de los expuestos aumenta, manteniendo una incidencia en no expuestos constante, el OR sobrestimará más al RR.
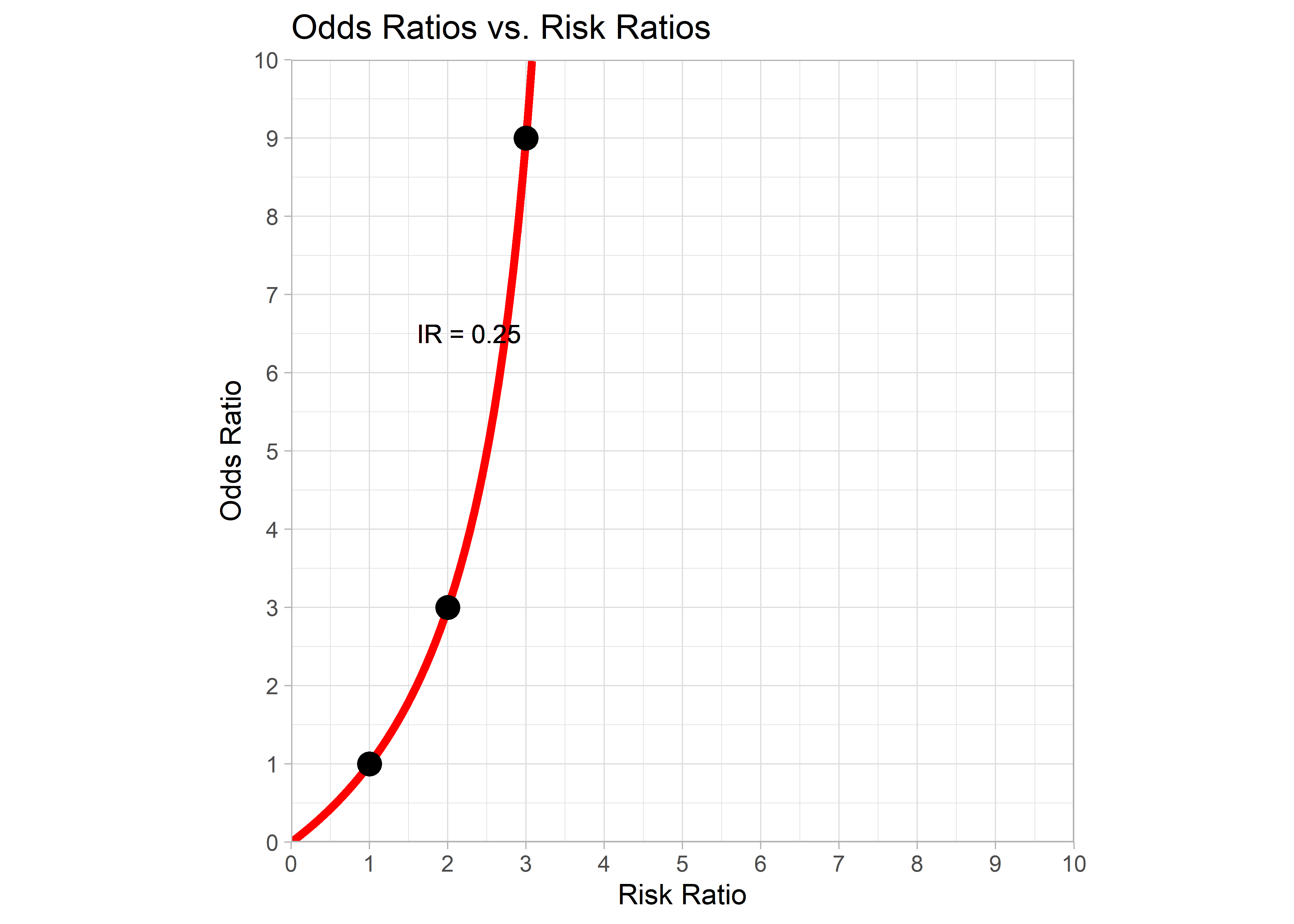
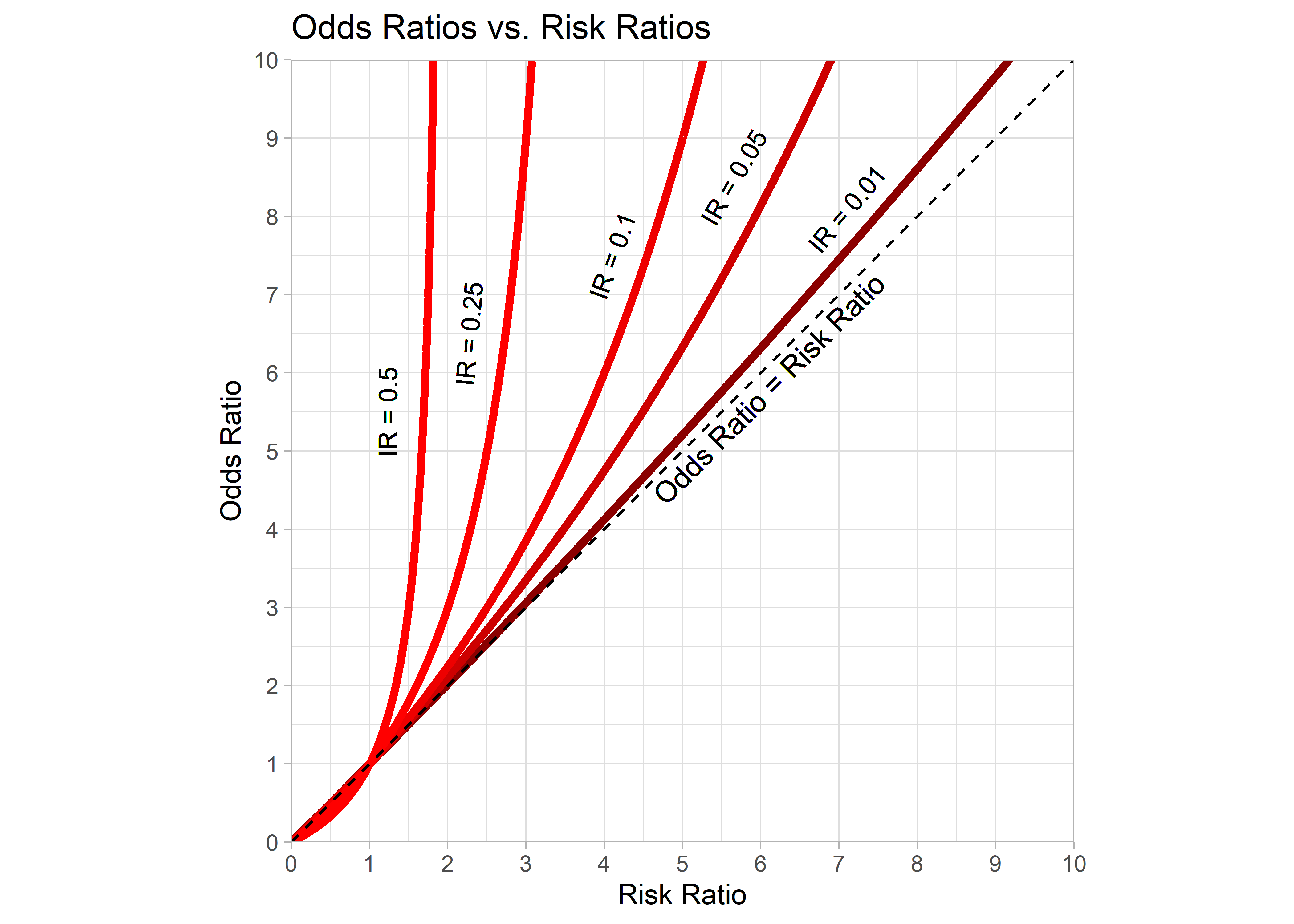
Si analizamos las diferencias entre el OR y RR en los distintos niveles de incidencia de casos en individuos no expuestos, podemos notar que a medida que esta última aumenta (25% vs 50%), la diferencia se hace más grande, mientras que cuando disminuye (25% vs 20% o menores), la diferencia entre el OR y RR se hace más pequeña, haciéndose semejante cuando la incidencia en no expuestos es menor a 1% e igual cuando es 0%.
17.8 Ejercicios
17.8.1 Ejercicio 1
Utilizando la base de datos de Framingham, para la variable cardiopatía coronaria prevalente (PREVCHD) calcule:
- Razón de prevalencia al basal y sexo como factor de exposición.
- Razón de Odds al basal y condición de fumador como factor de exposición.
- Razón de incidencias acumuladas en el segundo periodo y diabetes como factor de exposición.
Para la variable PREVCHD, “0” representa a los pacientes libres de enfermedad y “1”, a los pacientes diagnosticados con Angina de Pecho preexistente, Infarto de Miocardio (hospitalizado, silencioso o no reconocido) o Insuficiencia Coronaria (angina inestable).
17.8.2 Ejercicio 2
- Razón de tasa de incidencias para la variable Enfermedad Coronaria (ANYCHD) en función de la condición de diabetes. Hacer el cálculo para el segundo periodo de estudio.