14 Regresión logística: Conceptos básicos

Autores/as

Peña Calero, Brian Norman

Villa Almeyda, Diego

Carrasco Escobar, Gabriel

El análisis de regresión logística permite evaluar a las variables explicativas en función de una variable explicada/predicha que tiene una consideración categórica dicotómica, a diferencia de la regresión lineal en el que su variable explicada tiene una naturaleza contínua. Algunos ejemplos clásicos podrían serlo enfermo/sano, riesgo/sin riesgo, contagio/sin contagio, diabetes/sin diabetes, etc. Dicho de otra manera, se estudia de que manera una o más variables pueden contribuir para entender las probabilidades de que las observaciones pertenezcan a una categoría u otra.

Para ello, la regresión logística usa la función logística o sigmoidea para resolver el estudio de esta probabilidad de que una variable tome el valor de 0 o 1, mediante la siguiente formulación:

\[ P(Y = 1|x_1,x_2,...) = \frac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_{2}x_{2} + ... )}} \tag{14.1}\]

Donde:

\(P(Y = 1|x_1,x_2,...)\) es la probabilidad de que la observación pertenezca a la categoría 1 (estar enfermo por ejemplo) dado el valor en sus variables \(x_1\), \(x_2\), \(...\)
\(\beta_0\) es el intercepto
\(\beta_1\), \(beta_2\), \(...\) son los coeficientes de las variables \(x_1\), \(x_2\), \(...\)
\(e\) es la base del logaritmo natural

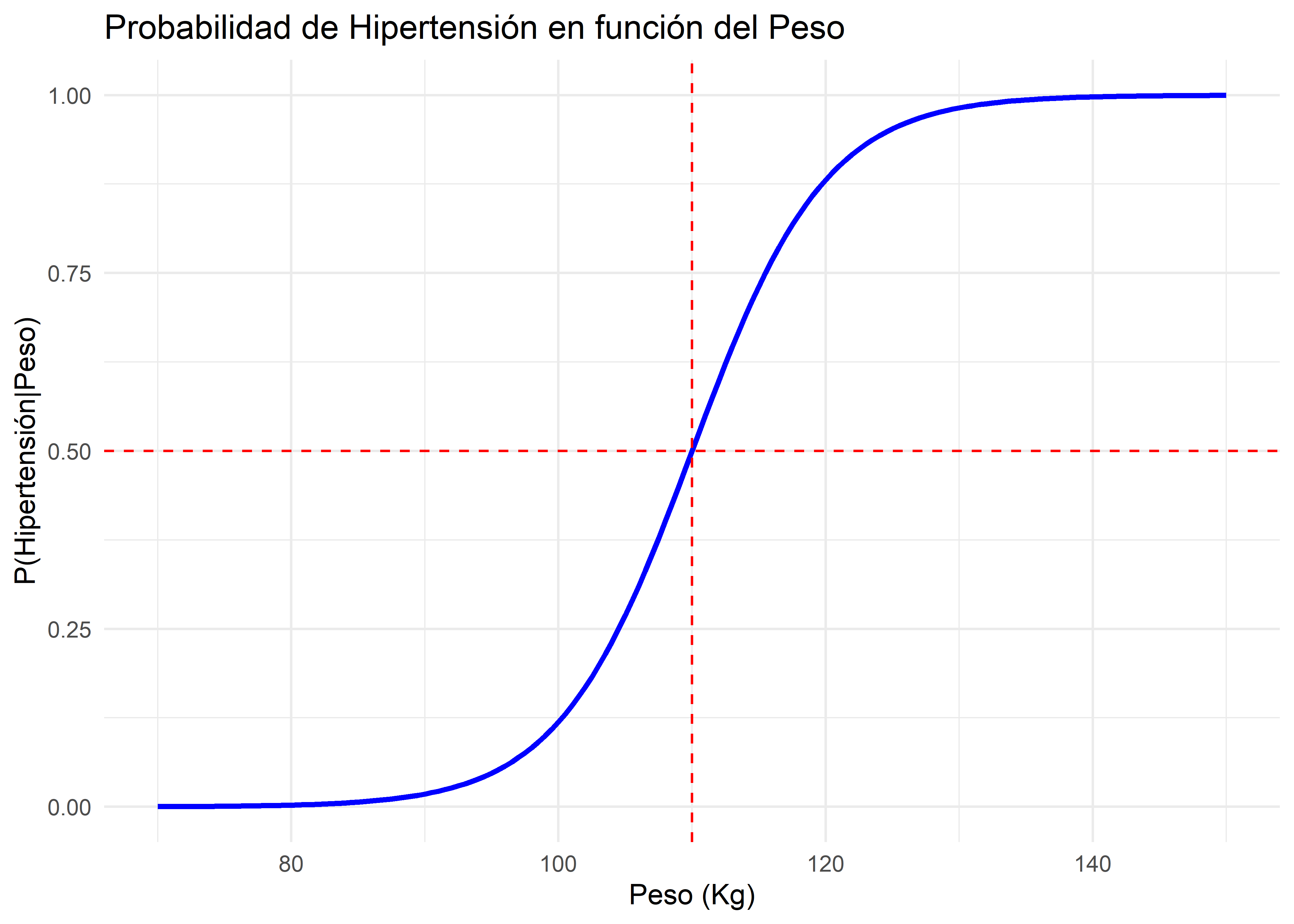
Por ejemplo, si estuviésemos relacionando como el peso en kg de las personas puede estar asociado a un mayor riesgo de hipertensión, la formulación anterior centrado en una sola variable explicativa podría verse de la siguiente manera:

Si bien es cierto, los coeficientes no guardan una relación lineal con respecto a la probabilidad, si lo hacen con respecto a los log-odds de la variable explicada:

\[ \mathrm{ln}\left(\frac{P(Y = 1|x_1,x_2,...)}{1-P(Y = 1|x_1,x_2,...)}\right) = ln(odds) = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + ... \tag{14.2}\]

Así, cada coeficiente de las variables explicativas (\(\beta_1\), \(beta_2\), \(...\)) estará representando el cambio log-odds o logits cuando haya un aumento en la unidad de sus respectivas variables (\(x_1\), \(x_2\), \(...\)). Veamos el desarrollo aplicado de este modelo con una base de datos real.

14.1 Paquetes y data

Los paquetes y bases de datos a ser utilizados en esta sección son:

library(tidyverse)
library(mlbench)
library(GGally)
library(broom)
library(jtools)

Usaremos el data set PimaIndiansDiabetes2 del paquete mlbench. Este data set contiene observaciones de 768 mujeres de más de 21 años del pueblo Pima que fueron parte de un estudio de cohorte realizado por el National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK) de los Estados Unidos en 1975. Este data set ha sido usado extensivamente para evaluar modelos de predicción de respuestas binarias. La variable de respuesta binaria en este caso es el diagnóstico de diabetes.

Una vez llamado el package mlbench, podemos cargar el data set usando la función data():

data("PimaIndiansDiabetes2")

También podemos importar la data del archivo diabetes.csv. Lo guardaremos en un objeto llamado diabetes:

diabetes <- read_csv("data/diabetes.csv")

Este data set contiene las siguientes variables:

pregnant: Número de veces que estuvo embarazada.
glucose: Concentración de glucosa en plasma (prueba de tolerancia a la glucosa).
pressure: Presión arterial diastólica (mm Hg).
triceps: Grosor del pliegue cutáneo del tríceps (mm).
insulin: Insulina sérica de 2 horas (mu U/ml).
mass: Índice de masa corporal (peso en kg/(altura en m)^2).
pedigree: Función de pedigrí de diabetes. Es una puntuación de la probabilidad de tener diabetes en función de los antecedentes familiares.
age: Edad en años.
diabetes: Diagnóstico de la prueba de diabetes.

La variable dependiente es diabetes, la cual toma los valores pos y neg si la mujer tenía diabetes o no, respectivamente. Transformaremos esta variable en un factor. Adicionalmente, con fines de la sesión vamos a eliminar las filas que contienen NA’s. Guarderemos estas transformaciones en un objeto llamado dm_data, por diabetes mellitus (DM):

dm_data <- diabetes %>%
  mutate(diabetes = factor(diabetes, 
                           levels = c("neg", "pos"))) %>%
  drop_na()

Revisar cuidadosamente los criterios para eliminar observaciones durante su proyecto de análisis.

14.2 Análisis exploratorio

Empecemos viendo la tabla de resumen de cada variable:

dm_data %>% 
  group_by(diabetes) %>% 
  skimr::skim()

Data summary
Name	Piped data
Number of rows	392
Number of columns	9
_______________________
Column type frequency:
numeric	8
________________________
Group variables	diabetes

Variable type: numeric

skim_variable	diabetes	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
pregnant	neg	1	2.72	2.62	0.00	1.00	2.00	4.00	13.00	▇▃▁▁▁
pregnant	pos	1	4.47	3.92	0.00	1.00	3.00	7.00	17.00	▇▂▃▁▁
glucose	neg	1	111.43	24.64	56.00	94.00	107.50	126.00	197.00	▂▇▅▂▁
glucose	pos	1	145.19	29.84	78.00	124.25	144.50	171.75	198.00	▂▅▇▇▆
pressure	neg	1	68.97	11.89	24.00	60.00	70.00	76.00	106.00	▁▂▇▆▁
pressure	pos	1	74.08	13.02	30.00	66.50	74.00	82.00	110.00	▁▂▇▅▁
triceps	neg	1	27.25	10.43	7.00	18.25	27.00	34.00	60.00	▅▇▆▃▁
triceps	pos	1	32.96	9.64	7.00	26.00	33.00	39.75	63.00	▂▆▇▅▁
insulin	neg	1	130.85	102.63	15.00	66.00	105.00	163.75	744.00	▇▂▁▁▁
insulin	pos	1	206.85	132.70	14.00	127.50	169.50	239.25	846.00	▇▅▁▁▁
mass	neg	1	31.75	6.79	18.20	26.13	31.25	36.10	57.30	▅▇▆▂▁
mass	pos	1	35.78	6.73	22.90	31.60	34.60	38.35	67.10	▃▇▂▁▁
pedigree	neg	1	0.47	0.30	0.09	0.26	0.41	0.62	2.33	▇▃▁▁▁
pedigree	pos	1	0.63	0.41	0.13	0.33	0.55	0.79	2.42	▇▅▂▁▁
age	neg	1	28.35	8.99	21.00	22.00	25.00	30.00	81.00	▇▂▁▁▁
age	pos	1	35.94	10.63	21.00	27.25	33.00	43.00	60.00	▇▇▅▃▂

Lo que más podemos destacar es que la mayoría de predictores tienen una dispersión bastante amplia, especialmente la variable insulin, que tiene un rango (p0 a p100) de 14 a 846 y una desviación estándar de 119. Esta gran dispersión en los predictores podría afectar la precisión de las estimaciones del modelo. Algunas soluciones para este caso son la estandarización (normalización) o categorización de los predictores. Además, podemos observar que la mayoría de las mujeres no tenían diabetes (67%).

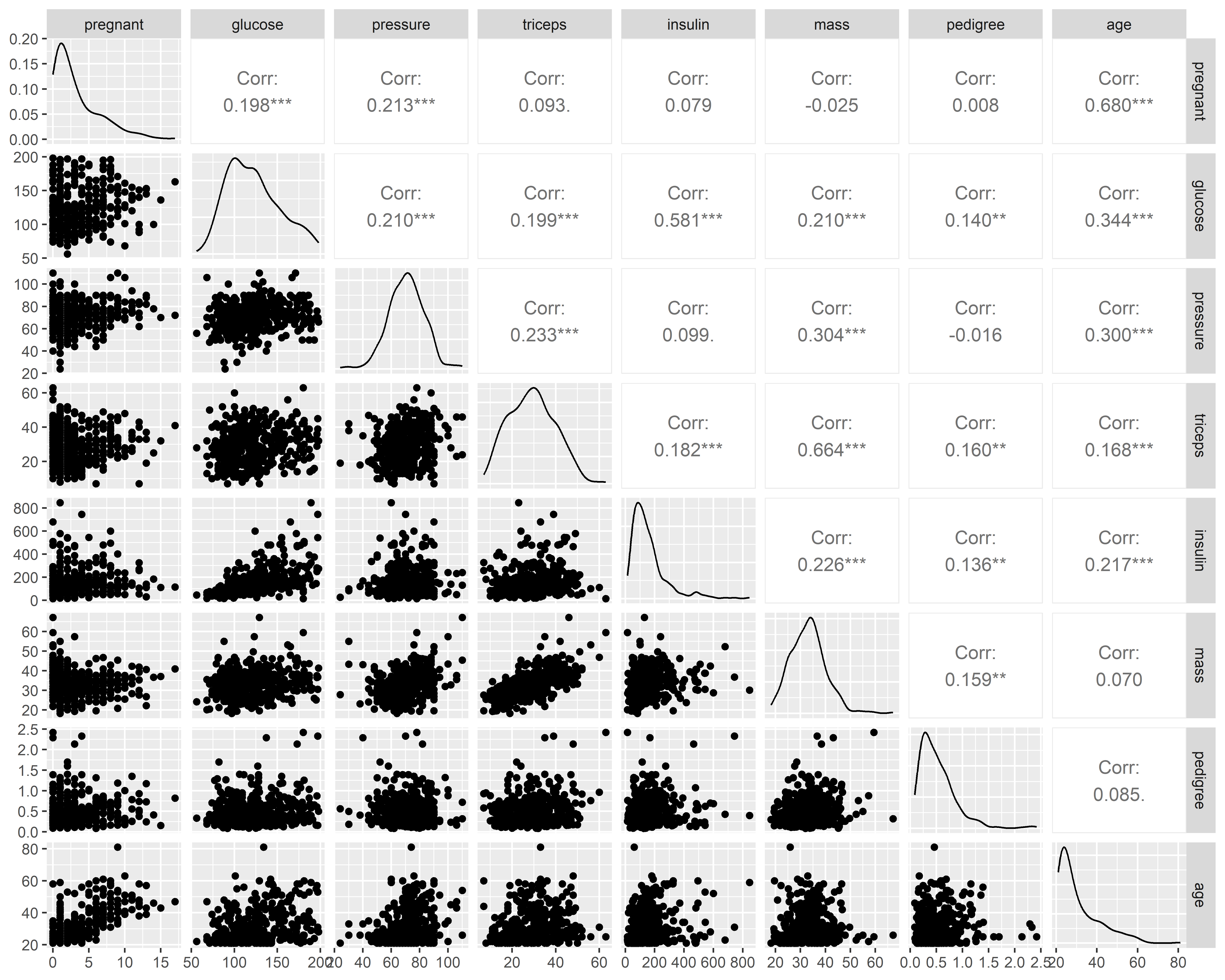
Veamos ahora un matriz gráfica de correlación para analizar la asociación entre los predictores usando la función ggpairs() del paquete GGally:

dm_data %>% 
  dplyr::select(-diabetes) %>% 
  ggpairs()

Vemos que las distribuciones de pregnant, insulin, mass, pedigree y age son bastante sesgadas hacia la derecha, lo cual podrían indicar la presencia de valores extremos. Las variables más correlacionadas son age y pregnant (0.68) y mass y triceps (0.664).

Veamos ahora la distribución de los predictores en cada clase de variable de respuesta. Usaremos gráficos de violín y box-plots para comparar las distribuciones en cada clase:

dm_data %>% 
  pivot_longer(-diabetes) %>% 
  ggplot(aes(diabetes, value, fill = diabetes)) +
  geom_violin() +
  geom_boxplot(aes(fill = diabetes), width = 0.1) +
  facet_wrap(~name, ncol = 2, scales = "free_y")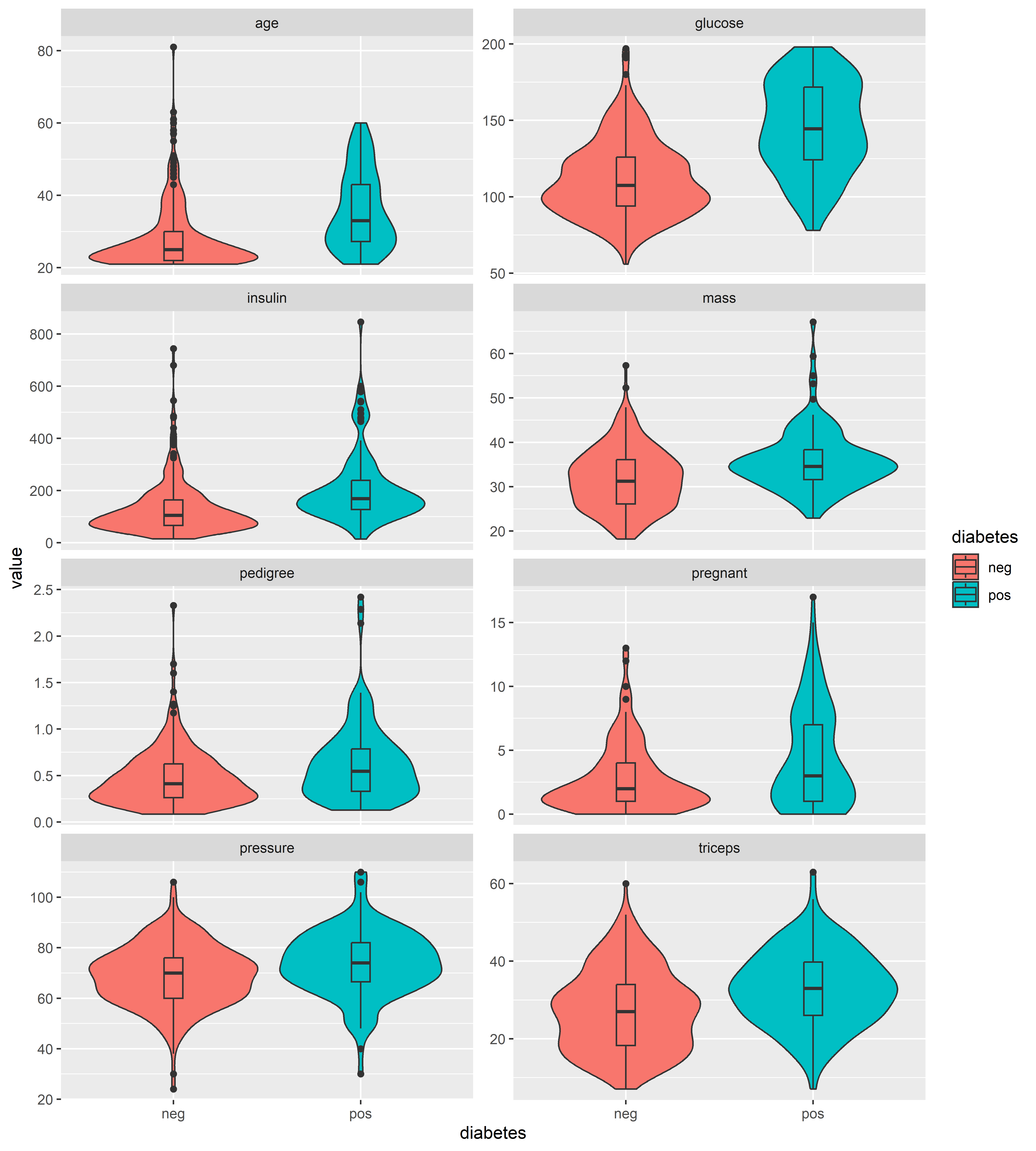

Confirmamos la presencia de valores extremos en los predictores mencionados anteriormente. En el caso de age, los outliers están presentes sobre todo en el grupo que no tiene diabetes. Exceptuando estos outliers, las mujeres con diabetes parecen tener en general mayor edad que las que no tienen. Esta misma tendencia se puede observar en la variable glucose. Para otras variables, no parece haber mucha diferencia en la distribución entre las que tienen y no diabetes.

14.3 Ajuste de un modelo de regresión logística

Para ajustar un modelo de regresión logística utilizamos la función base glm() de modelos lineales generalizados (generalized linear models en inglés). Al igual que con lm() para modelos de regresión lineal, en glm() especificamos la fórmula y la data a utilizar. La diferencia está que en el caso de glm() tenemos que especificar la familia de la distribución de la variable de respuesta usando el parámetro family. Para la regresión logística, el argumento que ingresemos debería ser family = binomial(link = 'logit') que usará el enlace logístico, sin embargo, si solo se especifica family = binomial, glm entenderá de forma predeterminada que el enlace a usar es el logit, por lo que se puede optar por no especificarlo.

El primer modelo consistirá en un modelo usando a todas las variables de dm_data como predictores sin transformar (~ .):

lrm_0 <- glm(diabetes ~ ., family = binomial, data = dm_data)
summary(lrm_0)


Call:
glm(formula = diabetes ~ ., family = binomial, data = dm_data)

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -1.004e+01  1.218e+00  -8.246  < 2e-16 ***
pregnant     8.216e-02  5.543e-02   1.482  0.13825    
glucose      3.827e-02  5.768e-03   6.635 3.24e-11 ***
pressure    -1.420e-03  1.183e-02  -0.120  0.90446    
triceps      1.122e-02  1.708e-02   0.657  0.51128    
insulin     -8.253e-04  1.306e-03  -0.632  0.52757    
mass         7.054e-02  2.734e-02   2.580  0.00989 ** 
pedigree     1.141e+00  4.274e-01   2.669  0.00760 ** 
age          3.395e-02  1.838e-02   1.847  0.06474 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 498.10  on 391  degrees of freedom
Residual deviance: 344.02  on 383  degrees of freedom
AIC: 362.02

Number of Fisher Scoring iterations: 5

Podemos observar que la evaluación de las variables pregnant, pressure, triceps y insulin no resultan significativos bajo un 0.05 de significancia en el modelo. Pese a ello, la residual deviance (cuanto el modelo no explica la variabilidad de los datos) es mucho menor en comparación a la nula deviance, por lo que lo que la consideración de dichas variables como predictoras está logrando contribuir al modelo en cierta medida.

A veces la valoración de los coeficientes y otros valores en el output de R base podría ser un poco más difícil de seguir, por lo que podemos usar la función tidy() del paquete broom para tener un output más directo:

tidy(lrm_0)

# A tibble: 9 × 5
  term          estimate std.error statistic  p.value
  <chr>            <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept) -10.0        1.22       -8.25  1.64e-16
2 pregnant      0.0822     0.0554      1.48  1.38e- 1
3 glucose       0.0383     0.00577     6.64  3.24e-11
4 pressure     -0.00142    0.0118     -0.120 9.04e- 1
5 triceps       0.0112     0.0171      0.657 5.11e- 1
6 insulin      -0.000825   0.00131    -0.632 5.28e- 1
7 mass          0.0705     0.0273      2.58  9.89e- 3
8 pedigree      1.14       0.427       2.67  7.60e- 3
9 age           0.0340     0.0184      1.85  6.47e- 2

Algo que no es tan evidente a primera vista es que el error estándar del coeficiente de pedigree es bastante alto (0.43) en comparación con los otros. Es decir, su estimación no es muy precisa. Esto puede deberse a muchas cosas, entre ellas la multicolinealidad, predictores con diferentes escalas y alta dispersión, pocos datos o datos no representativos, entre otros.

14.4 Transformaciones sobre los predictores

En algunos casos, la transformación a escala logarítmica logra mitigar el sesgo de las variables por valores extremos. Crearemos un nuevo objeto dm_log que ya no contenga dichas variables y transformaremos las variables numéricas a escala logarítmica:

dm_log <- dm_data %>% 
  dplyr::select(-c(pregnant, pressure, triceps, insulin)) %>% 
  mutate(
    across(where(is.numeric),
           ~ log(.x))
  )

Ajustemos un nuevo modelo con esta data:

lrm_1 <- glm(diabetes ~ ., family = binomial, data = dm_log)
summary(lrm_1)


Call:
glm(formula = diabetes ~ ., family = binomial, data = dm_log)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -39.2536     4.3640  -8.995  < 2e-16 ***
glucose       4.5713     0.6474   7.061 1.66e-12 ***
mass          2.7669     0.7173   3.858 0.000115 ***
pedigree      0.6473     0.2252   2.875 0.004044 ** 
age           2.1409     0.4809   4.452 8.51e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 498.10  on 391  degrees of freedom
Residual deviance: 340.03  on 387  degrees of freedom
AIC: 350.03

Number of Fisher Scoring iterations: 5

De esta manera podemos observar que la estimación del predictor pedigree ya no tiene un error estándar demasiado alto en comparación con los otros. Sin embargo, el error estándar del intercepto es mayor que en el resto de las variables por lo que podría haber una mayor incertidumbre sobre su estimación puntual.

Una forma de observar los coeficientes, errores estándar y poder compararlos entre las variables, es realizando un procedimiento de estandarización con ellas: \(\frac{x - \mu}{\sigma}\), donde \(\mu\) es la media de la variable y \(\sigma\) es la desviación estándar de la misma.

dm_std <- dm_data %>% 
  mutate(
    across(where(is.numeric),
           ~ (.x - mean(.x))/sd(.x))
  )

Probemos nuevamente un modelo con todas las variables originales, pero que ya pasaron el procedimiento de estandarización:

lrm_2 <- glm(diabetes ~ ., family = binomial, data = dm_std)
summary(lrm_2)


Call:
glm(formula = diabetes ~ ., family = binomial, data = dm_std)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -1.00026    0.14327  -6.981 2.92e-12 ***
pregnant     0.26385    0.17799   1.482  0.13825    
glucose      1.18103    0.17800   6.635 3.24e-11 ***
pressure    -0.01775    0.14787  -0.120  0.90446    
triceps      0.11801    0.17966   0.657  0.51128    
insulin     -0.09808    0.15526  -0.632  0.52757    
mass         0.49571    0.19215   2.580  0.00989 ** 
pedigree     0.39417    0.14767   2.669  0.00760 ** 
age          0.34633    0.18751   1.847  0.06474 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 498.10  on 391  degrees of freedom
Residual deviance: 344.02  on 383  degrees of freedom
AIC: 362.02

Number of Fisher Scoring iterations: 5

Vemos que los errores estándar se ven mejor, aunque el estado de la significatividad de las variables se mantienen exactamente igual, ya que la estandarización en sí no modifica esta evaluación. Ahora ajustemos un modelo solo con las variables significativas:

lrm_3 <- glm(
  diabetes ~ glucose + mass + pedigree + age, 
  family = binomial, data = dm_std
)
summary(lrm_3)


Call:
glm(formula = diabetes ~ glucose + mass + pedigree + age, family = binomial, 
    data = dm_std)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -0.9862     0.1417  -6.962 3.35e-12 ***
glucose       1.1168     0.1537   7.264 3.76e-13 ***
mass          0.5232     0.1424   3.673 0.000239 ***
pedigree      0.3756     0.1449   2.592 0.009541 ** 
age           0.5408     0.1371   3.945 8.00e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 498.10  on 391  degrees of freedom
Residual deviance: 347.23  on 387  degrees of freedom
AIC: 357.23

Number of Fisher Scoring iterations: 5

Como las variables se encuentran estandarizadas podremos valorar mejor sus estimaciones y sus errores estándar entre ellas así como poder compararlas. El error estándar del intercepto ahora es parecido al resto de las variables. Además, podemos señalar que la glucosa (glucose) es quien tiene un mayor efecto (mayor coeficiente) sobre la variable de respuesta.

14.5 Interacciones

Al igual que en los modelos de regresión lineal, podemos agregar interacciones entre predictores en un modelo de regresión logística. Exploremos qué pasa al agregar la interacción entre glucose y mass en el último modelo:

lrm_4 <- glm(
  diabetes ~ glucose*mass + pedigree + age, 
  family = binomial, data = dm_std
)
summary(lrm_4)


Call:
glm(formula = diabetes ~ glucose * mass + pedigree + age, family = binomial, 
    data = dm_std)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)   -1.0000     0.1451  -6.893 5.47e-12 ***
glucose        1.1915     0.1652   7.210 5.58e-13 ***
mass           0.5581     0.1436   3.887 0.000102 ***
pedigree       0.3939     0.1445   2.725 0.006423 ** 
age            0.5170     0.1381   3.745 0.000181 ***
glucose:mass  -0.2657     0.1695  -1.567 0.117041    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 498.1  on 391  degrees of freedom
Residual deviance: 344.8  on 386  degrees of freedom
AIC: 356.8

Number of Fisher Scoring iterations: 5

Vemos que en este caso, la interacción no resulta estadísticamente significativa, es decir que no hay evidencia estadística suficiente para aifrmar que el efecto de la glucosa (glucose) sobre el tener diabetes dependa o esté influenciado por el valor del índice de masa corporal (mass).

14.6 Interpretación del modelo

Usaremos la función summ() del paquete jtools para una salida más limpia del modelo. Por ejemplo, apliquémoslo en el modelo lrm_3 que es más sencillo de interpretar:

summ(lrm_3)

Observations	392
Dependent variable	diabetes
Type	Generalized linear model
Family	binomial
Link	logit

χ²(4)	150.86
Pseudo-R² (Cragg-Uhler)	0.44
Pseudo-R² (McFadden)	0.30
AIC	357.23
BIC	377.09

	Est.	S.E.	z val.	p
(Intercept)	-0.99	0.14	-6.96	0.00
glucose	1.12	0.15	7.26	0.00
mass	0.52	0.14	3.67	0.00
pedigree	0.38	0.14	2.59	0.01
age	0.54	0.14	3.94	0.00
Standard errors: MLE

De acuerdo a lo indicado en Ecuación 14.2, los resultados del tercer modelo lrm_3 puede expresarse de la siguinte manera:

\[ \mathrm{ln}(odds) = -0.99 + 1.12\times \mathrm{glucose} + 0.52\times \mathrm{mass} + 0.38\times \mathrm{pedigree} + 0.54\times \mathrm{age} \]

Los coeficientes de los predictores se interpretan como la cantidad que cambia el logit (log-odds) de diabetes con un cambio de una unidad en la escala de los predictores. Recordemos que las variables se encuentran estandarizadas, por lo que la unidad de cambio debe ser en la escala estándar (media 0 y desviación estándar 1).

Debido a que los coeficientes estan en escala logit utilizaremos el argumento exp = TRUE para generar las estimaciones de los odds ratios.

summ(lrm_3, exp = TRUE)

Observations	392
Dependent variable	diabetes
Type	Generalized linear model
Family	binomial
Link	logit

χ²(4)	150.86
Pseudo-R² (Cragg-Uhler)	0.44
Pseudo-R² (McFadden)	0.30
AIC	357.23
BIC	377.09

	exp(Est.)	2.5%	97.5%	z val.	p
(Intercept)	0.37	0.28	0.49	-6.96	0.00
glucose	3.06	2.26	4.13	7.26	0.00
mass	1.69	1.28	2.23	3.67	0.00
pedigree	1.46	1.10	1.93	2.59	0.01
age	1.72	1.31	2.25	3.94	0.00
Standard errors: MLE

Ahora podemos interpretar que para un aumento de una unidad (estándar) en la glucosa, los odds de tener diabetes (frente a no tener diabetes) aumentan por un factor de 3.06.

Para mayor detalle en la interpretación de los odds ratios puede visitar este link

Por último, podemos visualizar las estimaciones de los efectos usando la función plot_summs():

plot_summs(lrm_3)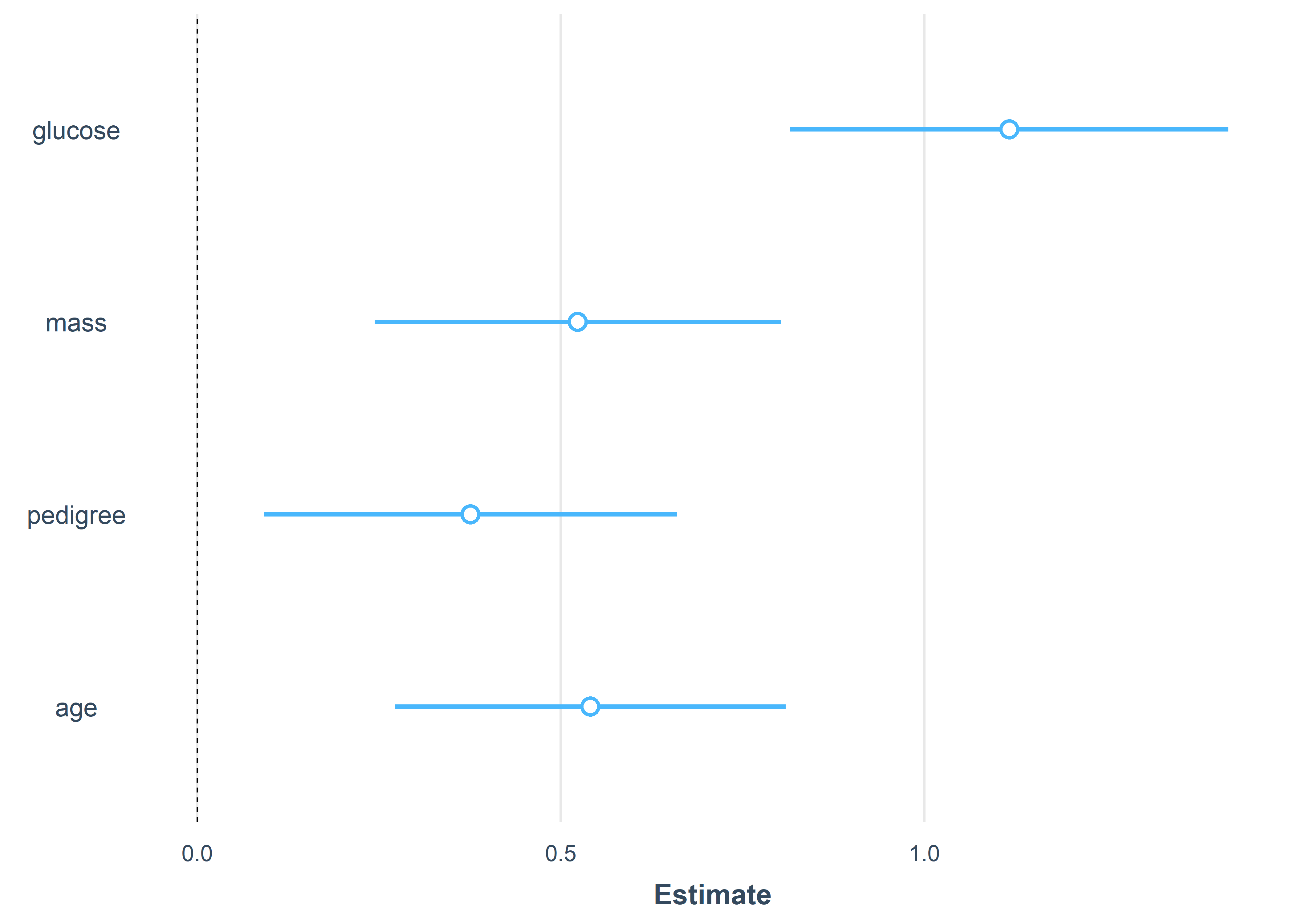

También en la escala de odds:

plot_summs(lrm_3, exp = TRUE)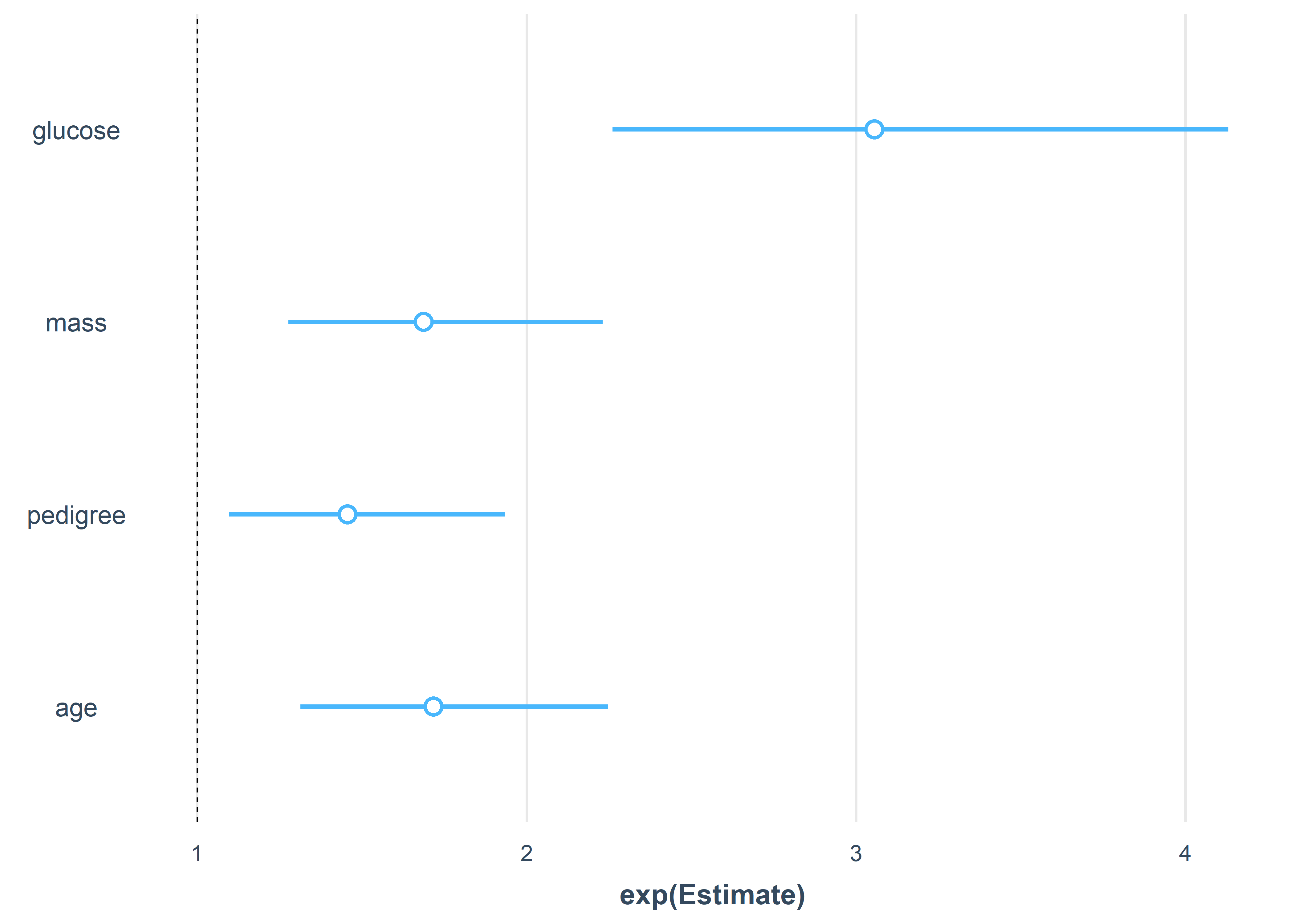

14.7 Predicción de Respuesta

Una vez evaluado el modelo logístico se podría generar sus valores predictivos en función del enlace (log-odds) resultantes para cada observación o en función de la respuesta (probabilidad de ser categorizado 1).

Aquí observaríamos las predicciones logits para cada observación debido al ajuste del modelo logístico lrm_3. Este uso no es tan común.

augment(lrm_3, type.predict = "link")

# A tibble: 392 × 11
   diabetes glucose   mass pedigree     age .fitted .resid    .hat .sigma
   <fct>      <dbl>  <dbl>    <dbl>   <dbl>   <dbl>  <dbl>   <dbl>  <dbl>
 1 neg       -1.09  -0.710  -1.03   -0.967   -3.48  -0.246 0.00350  0.948
 2 pos        0.466  1.42    5.11    0.209    2.31   0.435 0.0487   0.948
 3 pos       -1.45  -0.297  -0.796  -0.477   -3.31   2.59  0.00371  0.939
 4 pos        2.41  -0.368  -1.06    2.17     2.29   0.439 0.0169   0.948
 5 pos        2.15  -0.425  -0.362   2.76     2.55   0.388 0.0140   0.948
 6 pos        1.41  -1.04    0.185   1.97     1.18   0.733 0.0221   0.948
 7 pos       -0.150  1.81    0.0809  0.0133  -0.170  1.25  0.0185   0.946
 8 neg       -0.636  1.45   -0.984   0.209   -1.19  -0.728 0.0169   0.948
 9 pos       -0.247  0.215   0.0172  0.111   -1.08   1.66  0.00436  0.945
10 neg        0.109  0.884   0.524  -0.379   -0.410 -1.01  0.00879  0.947
# ℹ 382 more rows
# ℹ 2 more variables: .cooksd <dbl>, .std.resid <dbl>

Mientras que al especificar response, obtendremos las probabilidades estimadas de cada observación de ser categorizado como 1 en la variable respuesta. Dicho de otra manera, sería la probabilidad de cada observación de tener diabetes en función de las variables explicativas ingresadas.

augment(lrm_3, type.predict = "response")

# A tibble: 392 × 11
   diabetes glucose   mass pedigree     age .fitted .resid    .hat .sigma
   <fct>      <dbl>  <dbl>    <dbl>   <dbl>   <dbl>  <dbl>   <dbl>  <dbl>
 1 neg       -1.09  -0.710  -1.03   -0.967   0.0298 -0.246 0.00350  0.948
 2 pos        0.466  1.42    5.11    0.209   0.910   0.435 0.0487   0.948
 3 pos       -1.45  -0.297  -0.796  -0.477   0.0351  2.59  0.00371  0.939
 4 pos        2.41  -0.368  -1.06    2.17    0.908   0.439 0.0169   0.948
 5 pos        2.15  -0.425  -0.362   2.76    0.928   0.388 0.0140   0.948
 6 pos        1.41  -1.04    0.185   1.97    0.765   0.733 0.0221   0.948
 7 pos       -0.150  1.81    0.0809  0.0133  0.458   1.25  0.0185   0.946
 8 neg       -0.636  1.45   -0.984   0.209   0.233  -0.728 0.0169   0.948
 9 pos       -0.247  0.215   0.0172  0.111   0.253   1.66  0.00436  0.945
10 neg        0.109  0.884   0.524  -0.379   0.399  -1.01  0.00879  0.947
# ℹ 382 more rows
# ℹ 2 more variables: .cooksd <dbl>, .std.resid <dbl>

14.8 Ejercicios

La base de datos de casos de cáncer de mama en Wisconsin (Wisconsin breast cancer data) es usado para entrenamiento en la generación de modelos de clasificación. El objetivo es predecir si un tumor es benigno o maligno a partir de detalles de la biopsia.

Este data set se encuentra con el nombre BreastCancer en el paquete mlbench.

library(mlbench)

data("BreastCancer")
cancer <- BreastCancer
glimpse(cancer)

Rows: 699
Columns: 11
$ Id              <chr> "1000025", "1002945", "1015425", "1016277", "1017023",…
$ Cl.thickness    <ord> 5, 5, 3, 6, 4, 8, 1, 2, 2, 4, 1, 2, 5, 1, 8, 7, 4, 4, …
$ Cell.size       <ord> 1, 4, 1, 8, 1, 10, 1, 1, 1, 2, 1, 1, 3, 1, 7, 4, 1, 1,…
$ Cell.shape      <ord> 1, 4, 1, 8, 1, 10, 1, 2, 1, 1, 1, 1, 3, 1, 5, 6, 1, 1,…
$ Marg.adhesion   <ord> 1, 5, 1, 1, 3, 8, 1, 1, 1, 1, 1, 1, 3, 1, 10, 4, 1, 1,…
$ Epith.c.size    <ord> 2, 7, 2, 3, 2, 7, 2, 2, 2, 2, 1, 2, 2, 2, 7, 6, 2, 2, …
$ Bare.nuclei     <fct> 1, 10, 2, 4, 1, 10, 10, 1, 1, 1, 1, 1, 3, 3, 9, 1, 1, …
$ Bl.cromatin     <fct> 3, 3, 3, 3, 3, 9, 3, 3, 1, 2, 3, 2, 4, 3, 5, 4, 2, 3, …
$ Normal.nucleoli <fct> 1, 2, 1, 7, 1, 7, 1, 1, 1, 1, 1, 1, 4, 1, 5, 3, 1, 1, …
$ Mitoses         <fct> 1, 1, 1, 1, 1, 1, 1, 1, 5, 1, 1, 1, 1, 1, 4, 1, 1, 1, …
$ Class           <fct> benign, benign, benign, benign, benign, malignant, ben…

La variable a modelar es Class, la cual indica si el tumor es benigno o maligno. Entre las variables predictoras están el grosor del tumor (Cl.thickness), la uniformidad de la forma celular (Cell.shape), la cromatina blanda (Bl.cromatin), entre otras (help(BreastCancer) para mayor detalle).

El ejercicio es realizar el análisis de regresión logística para este data set. Debería incluir el análisis exploratorio, la selección de variables (elegir un método), diagnóstico, evaluación e interpretación del modelo seleccionado.