16 Medidas de frecuencia
16.1 Paquetes y data
Los paquetes que se utilizarán son:
En este capítulo utilizaremos la base de datos del estudio Framingham, el cual corresponde a una investigación prospectiva a largo plazo sobre las causas de las enfermedades cardiovasculares en una población de voluntarios sanos de Framingham, Massachusetts. Para mayor información sobre la documentación de esta base de datos, dar clic en este enlace.
framingham <- read_csv("data/framingham_freq_final.csv")16.2 Medidas de morbilidad
En esta sección, se revisarán los conceptos de prevalencia, odds e incidencia de una enfermedad y sus aplicaciones con R y Rstudio.
16.2.1 Prevalencia
Varias definiciones pueden referirse a “prevalencia” como el número de casos de una enfermedad o característica específica que se da en una población en un periodo determinado.
El siguiente gráfico muestra la distribución de 100 pacientes del estudio de Framingham en relación con su condición de angina de pecho.

La distribución revela que de los 100 pacientes estudiados, 5 tienen angina de pecho y 95 no cuentan con dicha condición. Estos datos son suficientes para calcular la prevalencia de angina de pecho en la muestra.
Matemáticamente una prevalencia es una proporción, por lo tanto, el numerador está incluido dentro del denominador. En este ejemplo, el numerador será el número de casos de la enfermedad y el denonimador la población total estudiada.
cases_angina <- 5
population <- 100Los objetos cases_angina y population ya pueden ser utilizados para calcular la prevalencia de angina de pecho.
prevalence_angina <- cases_angina / population
prevalence_angina[1] 0.05Luego del cálculo, se concluye que, en la población de estudio, la prevalencia de angina de pecho es del 5%.
16.2.2 Tipos de prevalencia
En la literatura existen dos tipos de prevalencia: Prevalencia puntual y de periodo.
La Prevalencia puntual es el porcentaje de una población que está enferma en un momento determinado en el tiempo, mientras que la prevalencia de periodo es el porcentaje de una población que padece una determinada enfermedad o afección a lo largo de un periodo de tiempo específico.
El siguiente gráfico muestra el seguimiento hecho a 5 sujetos durante 25 años para evaluar si tienen o desarrollan cáncer de pulmón a lo largo del estudio.
Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.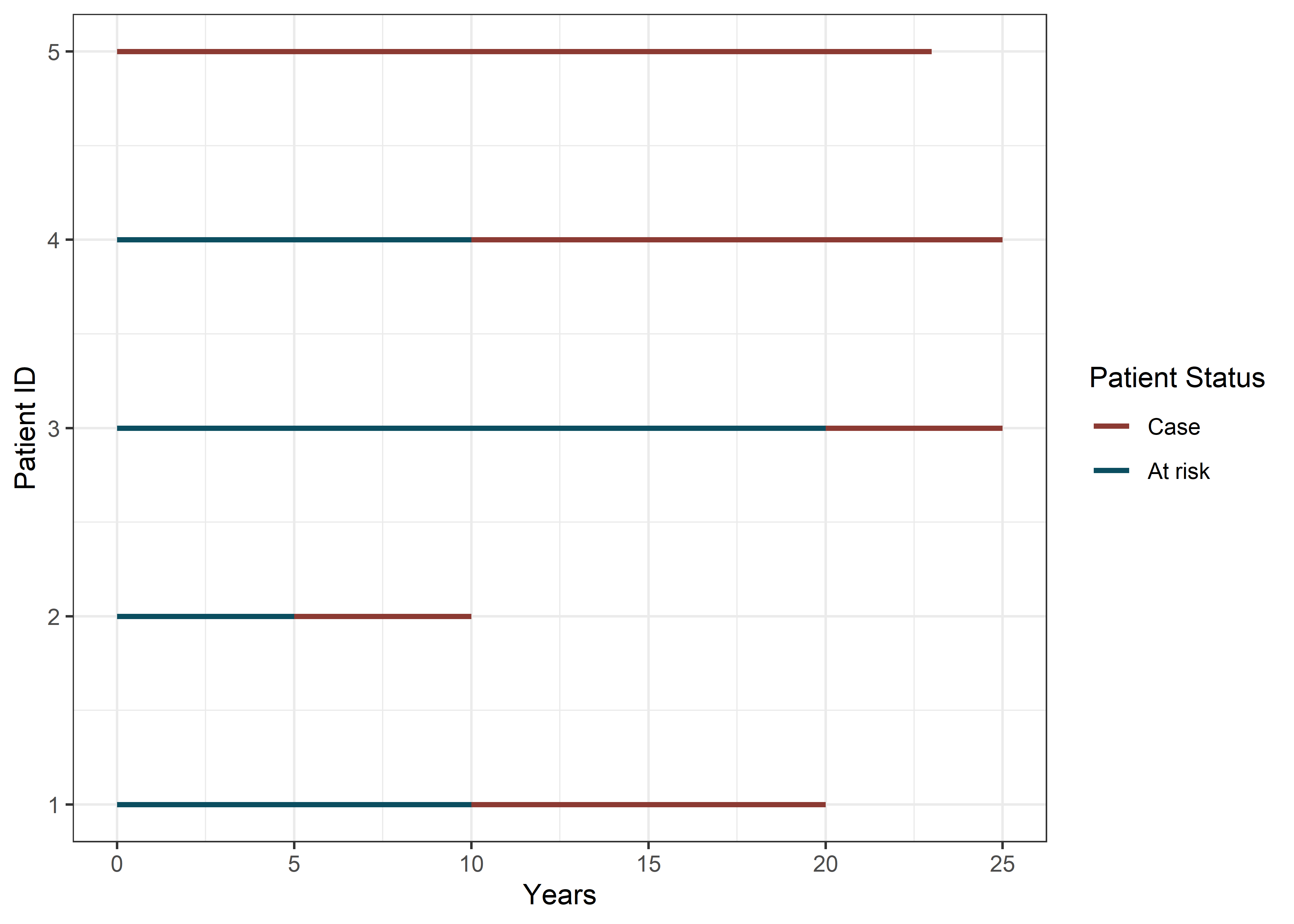
Cuando se estima la prevalencia puntual, el investigador desconoce a aquellos sujetos que son no susceptibles, por lo que, para el cálculo se incluyen a todos los sujetos que presenten la enfermedad para ese punto en el tiempo.
Ahora calcularemos la prevalencia puntual para el año 5 del seguimiento.
cases_cancer <- 2
population_cancer <- 5
point_prevalence <- (cases_cancer/population_cancer) * 100
point_prevalence[1] 40Interpretación: En la población de estudio, la prevalencia de cáncer de pulmón para el año 10 fue del 40%.
Al calcular la prevalencia de periodo, además de considerar los casos prevalentes, se deben incluir también a los casos nuevos que hayan presentado la enfermedad durante el periodo que se desea analizar. En el ejemplo anterior, podemos identificar a los casos prevalentes (sujeto 5) y a los casos incidentes (Sujeto 3 y Sujeto 1) que han sido incluidos para el cálculo de la prevalencia para el periodo comprendido entre el año 10 y 15.
cases_cancer_10_15 <- 4
population_10_15 <- 5
period_prevalence <- (cases_cancer_10_15 / population_10_15) * 100
period_prevalence[1] 80Interpretación: En la población de estudio, la prevalencia de cáncer de pulmón para para el periodo comprendido entre los años 10 y 15 fue del 80%.
16.2.2.1 Prevalencia puntual
En esta sección se calculará la prevalencia puntual de angina de pecho PREVAP en todos los participantes a los 0 días desde el enrolamiento, es decir al basal.
En esta sección se mostrarán dos maneras de calcular la prevalencia.
- Estimación de la prevalencia con
tidyverse() - Estimación de la prevalencia con
freq_table()
Estimación de la prevalencia con tidyverse
Las variables de importancia para el análisis de prevalencias e incidencias serán las siguientes,
- Angina Prevalente:
PREVAP - Sexo:
SEX - Stroke Prevalente:
PREVSTRK - Enfermedad Cerebro Vascular (ECV):
STROKE - Tiempo hasta desarrollar ECV:
TIMESTRK - Tiempo:
TIME - Periodo:
PERIOD
El código mostrado líneas abajo se utilizará para calcular la prevalencia puntual de angina al inicio del estudio. Este será un valor estimado para la población en general.
# Prevalencia puntual - Sin estratificación
angina_0 <- framingham_clean %>%
filter(TIME == 0) %>%
group_by(PREVAP) %>%
summarise(n = n())
prev_angina_total <- angina_0 %>%
mutate("prevalence" = n/sum(n)*100)
prev_angina_total# A tibble: 2 × 3
PREVAP n prevalence
<chr> <int> <dbl>
1 No 4287 96.7
2 Sí 147 3.32Interpretación: En la población de Framingham, la prevalencia basal de angina de pecho es de 3.32%.
A continuación, se mostrará el cálculo de la prevalencia de angina al inicio del estudio, pero se estratificará por sexo.
# Prevalencia puntual estratificada
angina_0_sex <- framingham_clean %>%
filter(TIME == 0) %>%
group_by(SEX, PREVAP) %>%
summarise(n= n())`summarise()` has grouped output by 'SEX'. You can override using the `.groups`
argument.prev_angina_sex <- angina_0_sex %>%
group_by(SEX) %>%
mutate("prevalence" = n/sum(n)*100)
prev_angina_sex# A tibble: 4 × 4
# Groups: SEX [2]
SEX PREVAP n prevalence
<chr> <chr> <int> <dbl>
1 female No 2435 97.8
2 female Sí 55 2.21
3 male No 1852 95.3
4 male Sí 92 4.73Al momento de estratificar, podemos observar que la prevalencia de angina en hombres es mayor a la prevalencia de angina en mujeres, 4.73% vs 2.21%, respectivamente.
Nota: Debemos tener en cuenta que las tablas anteriores muestran solo los estimados de las prevalencias sin sus respectivos intervalos de confianza. Las dos opciones siguientes para el cálculo de la prevalencia sí proporcionan intervalos de confianza.
Estimación de la prevalencia con el paquete freqtables
En esta sección se utilizará la función freq_table() del paquete freqtables para calcular la prevalencia puntual de angina de pecho PREVAP al basal (TIME == 0) y sus respectivos intervalos de confianza.
Para ello, utilizaremos la base de datos inicial de framingham y sobre ella haremos los cálculos.
framingham_clean %>%
filter(TIME == 0) %>%
freq_table(PREVAP)# A tibble: 2 × 9
var cat n n_total percent se t_crit lcl ucl
<chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 PREVAP No 4287 4434 96.7 0.269 1.96 96.1 97.2
2 PREVAP Sí 147 4434 3.32 0.269 1.96 2.83 3.88Para estratificar las prevalencias, solo se debe agregar a la función freq_table() la variable por la que se desea hacer la estratificación.
framingham_clean %>%
filter(TIME == 0) %>%
freq_table(SEX, PREVAP)# A tibble: 4 × 17
row_var row_cat col_var col_cat n n_row n_total percent_total se_total
<chr> <chr> <chr> <chr> <int> <int> <int> <dbl> <dbl>
1 SEX female PREVAP No 2435 2490 4434 54.9 0.747
2 SEX female PREVAP Sí 55 2490 4434 1.24 0.166
3 SEX male PREVAP No 1852 1944 4434 41.8 0.741
4 SEX male PREVAP Sí 92 1944 4434 2.07 0.214
# ℹ 8 more variables: t_crit_total <dbl>, lcl_total <dbl>, ucl_total <dbl>,
# percent_row <dbl>, se_row <dbl>, t_crit_row <dbl>, lcl_row <dbl>,
# ucl_row <dbl>Al revisar la columna percent_total, aparentemente las prevalencias han sido calculadas sin la estratificación por sexo. Sin embargo, el cálculo estratificado se encuentra almacenado en la columna percent_row, y los intervalos de confianza en las variables lci_row y uci_row.
16.2.2.2 Prevalencia de periodo
En esta sección solo se mostrará el cálculo de la prevalencia de periodo con la función freq_table(). Para este ejercicio solo nos centraremos en los casos de stroke en el periodo 3 (PERIOD == 3), el cual comprende un periodo de examinación de 8 años.
framingham_clean %>%
filter(PERIOD == 3) %>%
freq_table(STROKE)# A tibble: 2 × 9
var cat n n_total percent se t_crit lcl ucl
<chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 STROKE Sin Stroke 2980 3263 91.3 0.493 1.96 90.3 92.2
2 STROKE Stroke Incidente 283 3263 8.67 0.493 1.96 7.75 9.69Interpretación: La prevalencia de stroke durante el periodo 3 de la cohorte de Framingham fue de 8.67 (IC 95%: 7.75 - 9.69) casos por cada 100 habitantes .
16.2.3 Odds
Los odds son una medida de frecuencia de eventos. Matemáticamente representan una razón, es decir, los eventos en el numerador no están incluidos en el denominador.
Un ejemplo sencillo:
En una temporada del hipódromo, un caballo tuvo 15 victorias y 5 derrotas.
victorias <- 15
derrotas <- 5La proporción (ej. probabilidad) de victorias es:
p <- victorias / (victorias + derrotas)
p[1] 0.75El caballo ganó el
75%de carreras. En otras palabras, la probabilidad de que este caballo gane es del75%.
Los odds (ej. chances) de victorias son:
odds <- victorias / derrotas
odds[1] 3El caballo tiene unos odds de ganar de
3a1.
16.2.3.1 Relación con probabilidad
Los odds pueden expresarse matemáticamente en función de la probabilidad de la siguiente forma Ecuación 16.1:
Podemos comprobarlo con los datos de nuestro ejemplo inicial.
p / (1 - p)[1] 3odds == p / (1 - p)[1] TRUEDe forma complementaria, las probabilidades pueden expresarse matemáticamente en función de los odds de la siguiente forma Ecuación 16.2:
También podemos comprobarlo con los datos de nuestro ejemplo inicial.
odds / (1 + odds)[1] 0.75p == odds / (1 + odds)[1] TRUE16.2.3.2 Sesgo de estimación de los odds
Debido a su formula de cálculo Ecuación 16.1, los odds se aproximan mejor a las probabilidades cuando el evento es poco frecuente.
Un ejemplo sencillo:
En una temporada del hipódromo, un caballo tuvo 2 victorias y 100 derrotas.
victorias <- 2
derrotas <- 100La proporción (ej. probabilidad) de victorias es:
p <- victorias / (victorias + derrotas)
p[1] 0.01960784Y los odds (ej. chances) de victorias es:
odds <- victorias / derrotas
odds[1] 0.02En este nuevo ejemplo la probabilidad del evento (victorias) es bajo (0.0196) y los odds son cercanos (0.02).
Podemos simular diferentes frecuencias (ej. probabilidades de un evento), calcular los odds en base a la ecuación Ecuación 16.1 y graficarlo para mostrar el sesgo de estimación de los odds conforme aumenta la frecuencia del evento.
Podemos inspeccionar el gráfico cuando las frecuencias son menores a 50%
sim1 %>%
filter(p < 0.5) %>%
ggplot(aes(x = p, y = odds)) +
geom_line(col = "red") +
geom_abline(intercept = 0, slope = 1) +
theme_bw()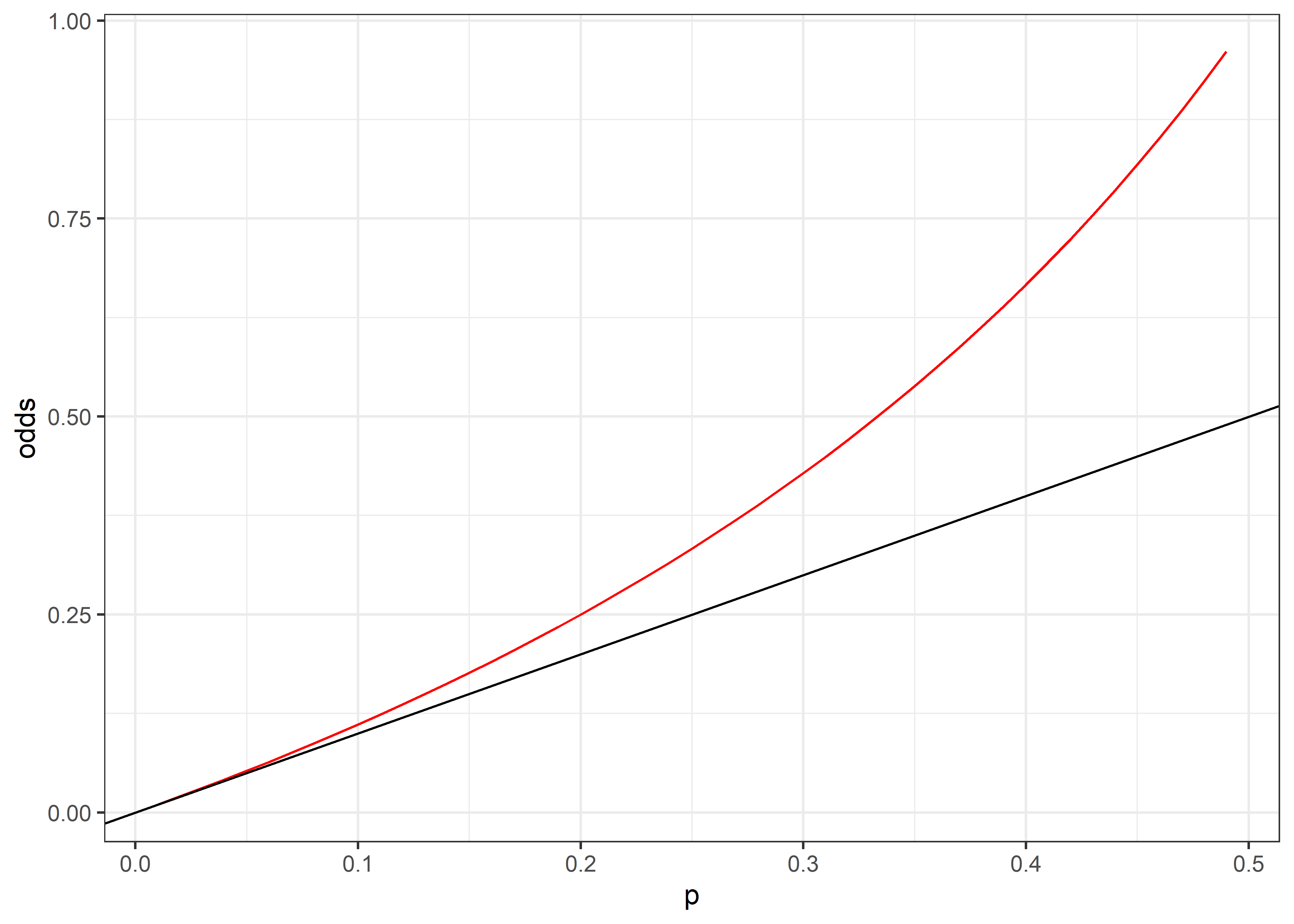
No hay una definición estricta, pero se sugiere que los odds se aproximan de forma estable a la probabilidad cuando la frecuencia del evento es menor al
10%.
Ahora veremos toda la distribución de frecuencias.
16.2.4 Incidencia
Cuando se observa a las personas a lo largo del tiempo, la incidencia mide la frecuencia con la que los individuos susceptibles se convierten en casos de enfermedad. Cuando cambia la susceptibilidad de una persona a la enfermedad, puede surgir un caso incidente. La cantidad de casos incidentes es el número total de tales ocurrencias en una población a lo largo de un tiempo de seguimiento predeterminado.
16.2.4.1 Incidencia acumulada (IA) o proporción de incidencia (PI)
Incidencia acumulada o proporción de incidencia: es el porcentaje de personas inicialmente vulnerables de una población que desarrollan nuevos casos en el transcurso de un tiempo de seguimiento determinado.
En este ejercicio, estimaremos la incidencia acumulada de hipertensión (HYPERTEN) para el periodo 3 (PERIOD==3) del estudio. Recordemos que el cálculo de la incidencia solo toma en cuenta a casos nuevos en el numerador, y solo a las personas susceptibles a volverse casos en el denominador. Por ello, primero retiraremos a todos los casos prevalentes de hipertensión (PREVHYP), y posteriormente filtraremos el periodo de interés.
Una vez que se haya retirado a todos los individuos que tenían hipertensión al inicio del estudio y tengamos nuestro periodo de interés, procederemos a realizar la estimación de la incidencia de hipertensión.
El cálculo de la incidencia solo con tidyverse seguirá el siguiente flujo de código,
# A tibble: 2 × 3
HYPERTEN n incidence
<chr> <int> <dbl>
1 Hipertension Incidente 501 38.2
2 Sin Hipertension 809 61.8Como la incidencia acumulada es matemáticamente una proporción el método de cálculo es el mismo que el de la prevalencia.
Ahora, realizaremos el cálculo usando el paquete freq_table().
free_prev_hyper %>%
freq_table(HYPERTEN)# A tibble: 2 × 9
var cat n n_total percent se t_crit lcl ucl
<chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 HYPERTEN Hipertension Incidente 501 1310 38.2 1.34 1.96 35.6 40.9
2 HYPERTEN Sin Hipertension 809 1310 61.8 1.34 1.96 59.1 64.4Durante el periodo 3 del estudio de Framingham, se observó una incidencia acumulada del 38.24% (IC 95%: 35.65 - 40.91). Es decir, por cada 100 personas, hubieron aproximadamente 38 casos nuevos de hipertensión.
16.2.4.2 Tasa de incidencia (TI) o densidad de incidencia (DI)
La tasa de incidencia expresa la ocurrencia de casos nuevos de una determinada enfermedad o evento entre el total de personas-tiempo en seguimiento.
El denominador de la tasa de incidencia se calcula sumando los periodos de tiempo sin enfermedad de cada uno de los participantes del grupo durante el tiempo en que permanecen en el estudio. Este valor se suele expresar en años, aunque también puede ser en meses, semanas o días, y se denomina tiempo en riesgo o tiempo en seguimiento.
Evaluaremos la densidad de incidencia de stroke en el periodo 3 del estudio. Para ello, seguiremos utilizando el objeto framingham_clean creado al inicio del capítulo, y lo asignaremos al objeto incidence_strk. Se removerá a todos los pacientes que hayan tenido STROKE al inicio del estudio, y solo nos centraremos en el periodo 3.
El objeto incidence_strk ahora solo contiene a las personas libres de STROKE al basal. Ahora se realizará el cálculo de los casos y los tiempos totales aportados los pacientes al estudio.
incidence_strk_cases <- incidence_strk %>%
group_by(STROKE) %>%
summarise(cases = n(),
follow_up_time = sum(TIMESTRK))
incidence_strk_cases# A tibble: 2 × 3
STROKE cases follow_up_time
<chr> <int> <dbl>
1 Sin Stroke 2980 24855611
2 Stroke Incidente 214 1421969Las variables cases y follow_up_time contienen la información necesaria para el cálculo de la densidad de incidencia.
inc_dens <- incidence_strk_cases %>%
mutate(incidence_density = cases/follow_up_time*100000)
inc_dens# A tibble: 2 × 4
STROKE cases follow_up_time incidence_density
<chr> <int> <dbl> <dbl>
1 Sin Stroke 2980 24855611 12.0
2 Stroke Incidente 214 1421969 15.0En la población de estudio, la tasa de incidencia de stroke es de 15 casos por cada 100,000 personas-días.
16.2.5 Incidencia vs prevalencia vs odds
En el presente gráfico, se observan las medidas de frecuencia asociadas a la angina de pecho. Al analizar la evolución temporal, se destaca un aumento progresivo en la prevalencia de la enfermedad, observada de manera mensual. En contraste, la incidencia y el odds de angina se mantienen relativamente constantes a lo largo del periodo de estudio.
Rows: 11631 Columns: 42
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (39): RANDID, SEX, AGE, CIGPDAY, BMI, DIABETES, PREVHYP, PERIOD, HYPERT...
date (3): START_DATE, VISIT_DATE, EVENT_CENSOR_DATE
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.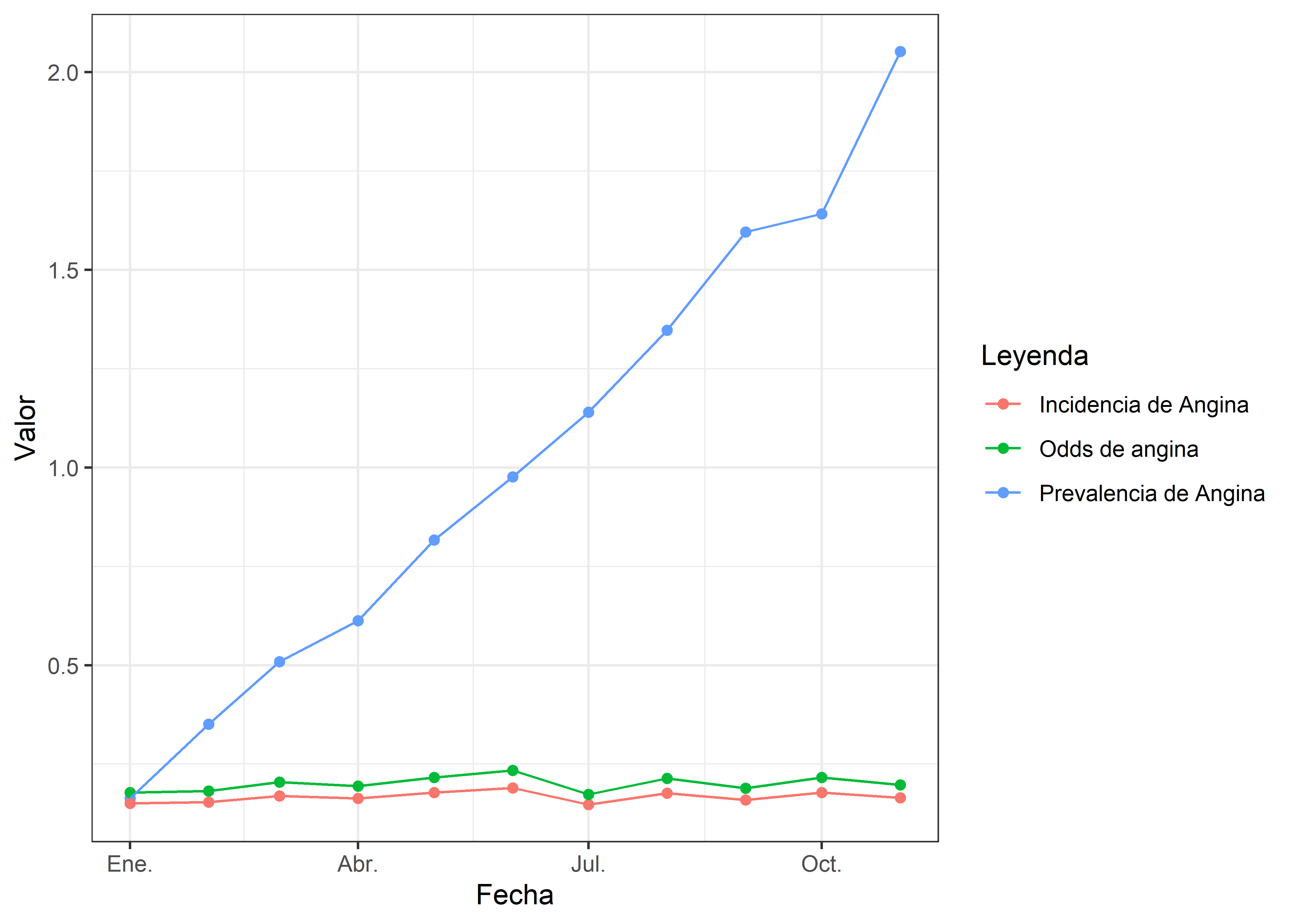
16.3 Medidas de mortalidad
Normalmente, para notificar la mortalidad se utiliza el número de defunciones en una población de un tamaño determinado.
16.3.1 Tasa de mortalidad
La tasa de mortalidad se refiere a la cantidad de muertes en una población durante un período de tiempo determinado, generalmente expresada como un número de muertes por cada mil o cada cien mil personas en la población en riesgo.
Utilizaremos el objeto framingham, seleccionaremos nuestras variables de interés para toda la sección de mortalidad y eliminaremos los datos faltantes.
Variables a utilizar:
- Muerte:
DEATH - Edad categórica:
AGE_CAT - Periodo:
PERIOD - Paciente con Infarto:
ANYCHD - Muerte por infarto:
MI_FCHD
Para el presente ejercicio, se calculará la tasa de mortalidad general en el estudio Framingham para el periodo 3, PERIOD == 3.
Ahora se calcularán los conteos de los conteos de muertes y no muertes en la población de estudio para el periodo 3.
# A tibble: 2 × 2
DEATH n
<chr> <int>
1 Alive 2488
2 Dead 775Finalmente, realizaremos el cálculo de la mortalidad,
# A tibble: 2 × 3
DEATH n mortality
<chr> <int> <dbl>
1 Alive 2488 76.2
2 Dead 775 23.8Ahora se realizará el cálculo con la función freq_table() del paquete freqtables.
mortality %>%
freq_table(DEATH)# A tibble: 2 × 9
var cat n n_total percent se t_crit lcl ucl
<chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 DEATH Alive 2488 3263 76.2 0.745 1.96 74.8 77.7
2 DEATH Dead 775 3263 23.8 0.745 1.96 22.3 25.2Durante el periodo 3 del estudio de Framingham, se observó una tasa de mortalidad del 23.75%. Es decir, por cada 100 personas, hubo aproximadamente 24 (IC 95%: 22.32 - 25.24) muertos.
16.3.2 Tasa de mortalidad específica
La tasa de mortalidad específica se refiere a la cantidad de muertes en una subpoblación específica; por ejemplo, las muertes por una enfermedad específica o en un grupo de edad específico durante un periodo de tiempo determinado.
Para este ejercicio, calcularemos la tasa de mortalidad específica por grupos de edad.
`summarise()` has grouped output by 'AGE_CAT'. You can override using the
`.groups` argument.mortality_age# A tibble: 4 × 3
# Groups: AGE_CAT [2]
AGE_CAT DEATH n
<chr> <chr> <int>
1 mayor o igual a 60 Alive 1080
2 mayor o igual a 60 Dead 593
3 menor de 60 Alive 1408
4 menor de 60 Dead 182Una vez que tenemos la base de datos preparada, podemos calcular la mortalidad específica por grupos de edad.
# A tibble: 4 × 4
# Groups: AGE_CAT [2]
AGE_CAT DEATH n mortality
<chr> <chr> <int> <dbl>
1 mayor o igual a 60 Alive 1080 64.6
2 mayor o igual a 60 Dead 593 35.4
3 menor de 60 Alive 1408 88.6
4 menor de 60 Dead 182 11.4El código para obtener los estimados de la mortalidad con la función freq_table() será el siguiente,
mortality %>%
freq_table(AGE_CAT, DEATH)# A tibble: 4 × 17
row_var row_cat col_var col_cat n n_row n_total percent_total se_total
<chr> <chr> <chr> <chr> <int> <int> <int> <dbl> <dbl>
1 AGE_CAT mayor o ig… DEATH Alive 1080 1673 3263 33.1 0.824
2 AGE_CAT mayor o ig… DEATH Dead 593 1673 3263 18.2 0.675
3 AGE_CAT menor de 60 DEATH Alive 1408 1590 3263 43.2 0.867
4 AGE_CAT menor de 60 DEATH Dead 182 1590 3263 5.58 0.402
# ℹ 8 more variables: t_crit_total <dbl>, lcl_total <dbl>, ucl_total <dbl>,
# percent_row <dbl>, se_row <dbl>, t_crit_row <dbl>, lcl_row <dbl>,
# ucl_row <dbl>Es importante recordar que cuando se utilice la función freq_table() y se estratifique el estimado, debemos revisar las columnas percent_row, lcl_row y ucl_row.
16.3.3 Tasa de letalidad
La tasa de letalidad es el cálculo de la proporción de personas que han fallecido a causa de una enfermedad en relación al número de personas que han sido diagnosticadas con dicha enfermedad.
MI_FCHD y pacientes con infarto agudo al miocardio ANYCHD. Para ello, solo nos enfocaremos en los pacientes que han tenido infarto ANYCHD == "Infarto".
Ahora se realizará el conteo de muertes
# A tibble: 2 × 2
MI_FCHD n
<chr> <int>
1 Muerte 453
2 No Muerte 394Posteriormente, se calculará la tasa de letalidad.
# A tibble: 2 × 3
MI_FCHD n fatality
<chr> <int> <dbl>
1 Muerte 453 53.5
2 No Muerte 394 46.5Usando freq_table()
letalidad %>%
freq_table(MI_FCHD)# A tibble: 2 × 9
var cat n n_total percent se t_crit lcl ucl
<chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 MI_FCHD Muerte 453 847 53.5 1.71 1.96 50.1 56.8
2 MI_FCHD No Muerte 394 847 46.5 1.71 1.96 43.2 49.9En la población de estudio, la tasa de letalidad de infarto agudo al miocardio es de 53.48% (IC95%: 50.11 - 56.83).
16.4 Ejercicios
16.4.1 Ejercicio 1
Utilizando la base de datos de Framingham, calcule:
- Prevalencia puntual al inicio del estudio de infarto al miocardio
16.4.2 Ejercicio 2
- Prevalencia de hipertensión en el periodo 2
16.4.3 Ejercicio 3
- Incidencia de stroke en el periodo 3