27 Introducción a inferencia causal

Autores/as

Carrasco Escobar, Gabriel

Fernandez Camacho, Bryan

27.1 General

En julio de 2023, el estreno simultáneo en cines de dos películas, Barbie de Warner Bros. Pictures y Oppenheimer de Universal Pictures, generó un fenómeno cultural conocido como Barbenheimer. Ambas películas tienen una trama muy diferente y su público objetivo es de cierta forma opuesto. A pesar de estas diferencias, ambas productoras tuvieorn fuertes disputas en terminos de taquilla y críticas.

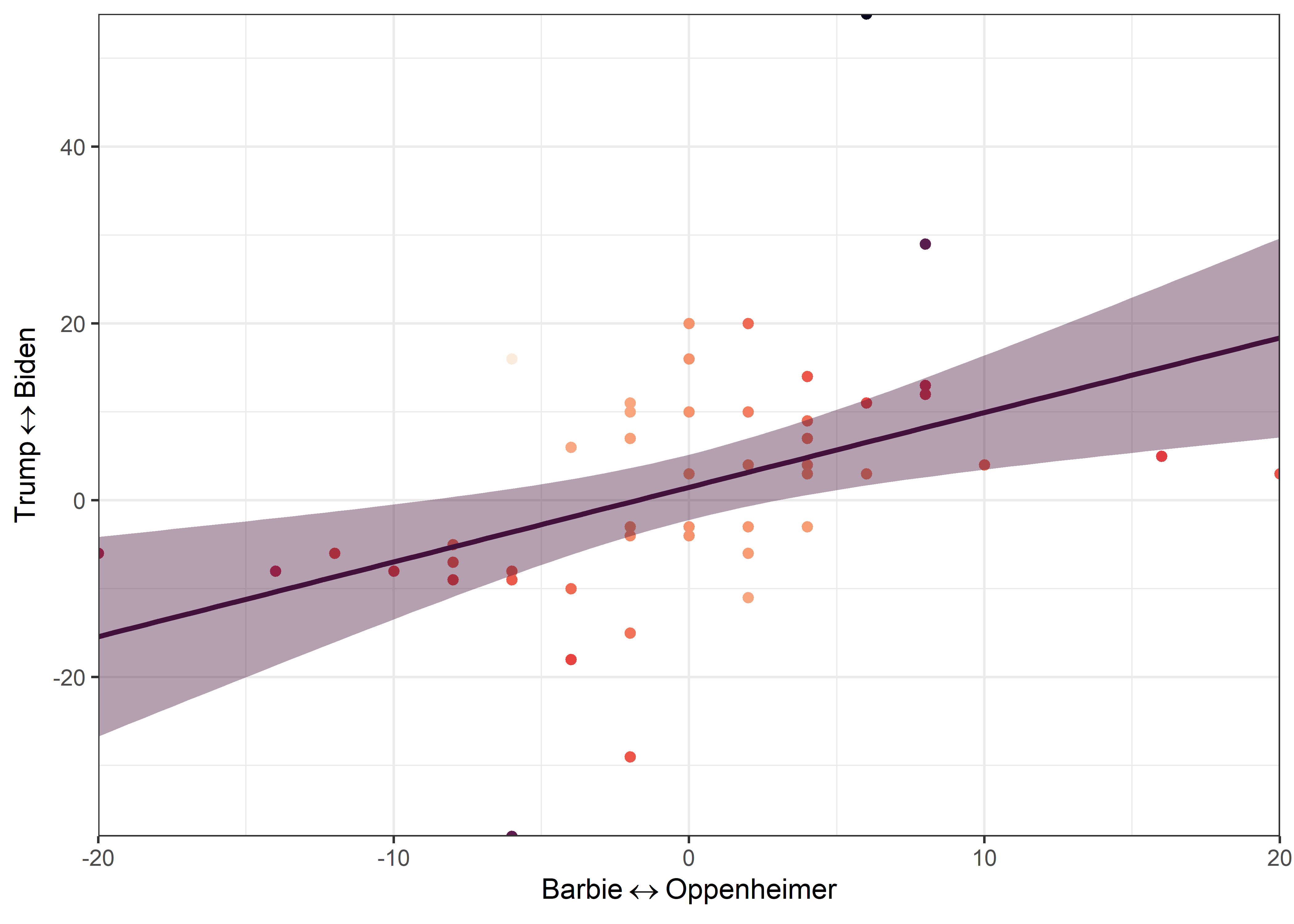
Muy pronto, usuarios de redes sociales empezaron a notar las semejanzas entre las tendencias de ambas películas (medidos por Google Trends) y los resultados de las elecciones presidenciales del 2020 en Estados Unidos.

Incluso, los datos de ambas métricas tienen una tendencia positiva marcada:

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	1.4766810	1.8364273	0.8041053	0.4252202	-2.2137579	5.16712
barbenheimer_index	0.8446357	0.2648492	3.1891196	0.0024883	0.3124013	1.37687

Entonces, ¿Existe alguna relación entre ambas variables?

¿La información contenida en una de estas variables nos va a permitir conocer un poco de la información en la otra variable? O si pudieramos, ¿al modificar (o intervenir) una de estas variables generaremos un cambio en la otra?

Este ejemplo, nos permite reflexionar que un modelo de regresión se utiliza, principalmente, para predecir el valor de una variable de desenlace en función de una o más variables explicativas. Como comentamos anteriormente, los modelos de regresión abordan un problema mecánico simple, que es, cuál es nuestra mejor estimación de y dada una x observada.

La regresión puede utilizarse sin pensar en las causas como una herramienta predictiva o de resumen.
No sería apropiado dar interpretaciones causales a ningún coeficiente, a menos que establezcamos el cumplimiento de ciertos supuestos (de identificación).

Miguel Hernan (2019) propone una clasificación para las tareas de ciencia de datos en salud que consiste en 3 tipos:

Tareas de descripción
Tareas de predicción
Tareas de Inferencia causal

Una misma herramienta (ej. modelo de regresion, machine learning, etc.) podría eventualmente usarse para cualquiera de las 3 tareas. El uso de la herramienta, no define el proposito de la tarea de análisis que deseamos conducir. Por lo tanto, el primer paso es siempre definir cuál de estos tipos de investigación queremos conducir, y utilizar las herramientas adecuadas con los criterios y supuestos adecuados.

27.2 Asociación y Causalidad

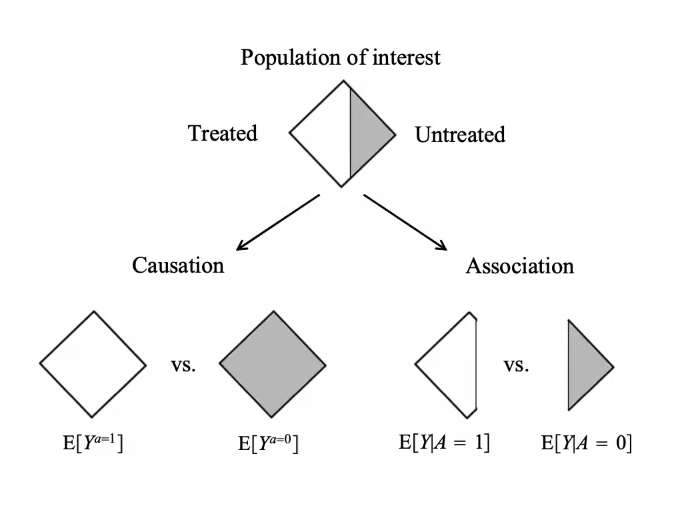
Cuando hablamos de asociación solo nos estamos refiriendo a la vinculación numérica o estadística que existe entre dos variables. Mientras que cuando nos referimos a causalidad, estamos hablando que, además de la vinculación numérica, existe un mecanismo causal que explica la asociación entre la variable de exposición y la variable desenlace.

Imaginemos que nuestra población de estudio está conformada por personas mayores de 18 años y queremos evaluar la mortalidad como variable desenlace y la condición de vacunación como variable princial. Siendo vacunado = Treated, No vacunado = Untreated. Con los datos del estudio, solo podremos determinar una asociación, debido a que la población se dividirá en función a la exposición, conformando así un escenario factual, el cual contiene los datos reales.

Para la inferencia causal, la lógica del análisis es distinta ya que no se busca comparar a dos grupos de personas distintas, sino, comparar el grupo de personas cuando todos han sido vacunados contra el “mismo” grupo de personas cuando ninguno ha sido vacunado, conformando así un escenario contrafactual, el cual, a través de las herramientas de análisis utilizadas, contiene una pseudo-población Hernán & Robins, 2024.

27.3 Marco contrafactual

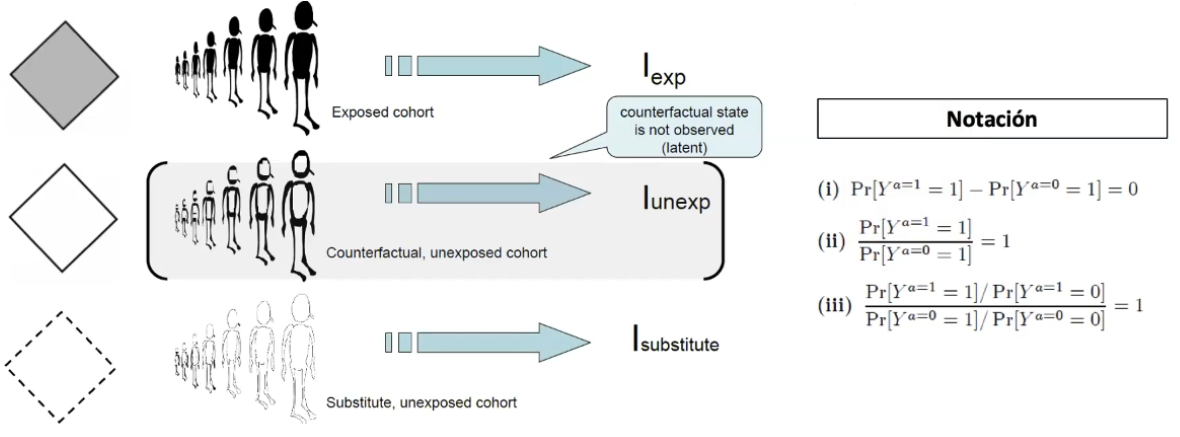
Uno de los marcos más comunes para identificar efectos causales es el basado en la noción de contrafactuales hipotéticos. Dentro del modelo contrafactual, los efectos causales están definidos como el contraste entre dos desenlaces, el observado (factual) y el no observado (contrafactual).

El problema fundamental de la inferencia causal, por definición, es que los desenlaces contrafactuales son imposibles de observar (Holland, 1986). Idealmente tendríamos un grupo de personas que recibe el tratamiento, y el mismo grupo de personas que no recibe el tratamiento. Sin embargo, en la realidad eso no sucederá. Por tal motivo, en epidemiología se recurre al grupo sustituto, el cual está conformado por un grupo de personas diferentes pero que son semenjantes a las personas del grupo contrafactual.

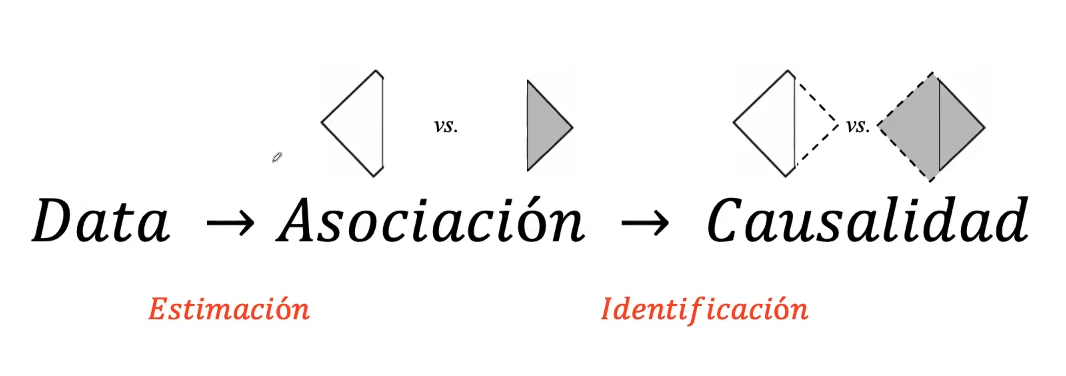
Tanto para asociaciones como para inferencias causales se parte de los datos. El siguiente paso luego de obtener los datos será realizar la asociación a través de un proceso llamado estimación. Finalmente, pasaremos de una asociación a la inferencia causal a través de un proceso llamado identificación.

27.4 Estrategias de identificación

Al partir de datos observacionales, una estrategia para identificar el efecto causal es el uso de grafos acíclicos dirigidos, o DAG por sus siglas en inglés. Los DAGs son representaciones esquemáticas no paramétricas del proceso de generación de datos propuesto para un conjunto de variables aleatorias, y sus mediciones, en un contexto específico. En otras palabras, los DAGs pueden ser entendidos también como la representación de la hipótesis de investigación formulada con la estructura causal de nuestros datos.

Además, cada DAG representa un modelo causal subyacente, es decir, conforma una estrategia de identificación, ya que, lo que se añade al grafo realmente es la estructura causal que se desea identificar.

Esta herramienta es útil en el campo de la investigación epidemiológica debido a que permite hacer explícita la red causal, sintetiza los conocimientos previos y supuestos sobre un tema en específico, mejora la comunicación entre los investigadores y es intuitiva y fácil de usar.

Qué no es un DAG

En muchas ocasiones, los DAG pueden ser confundidos con gráficos, pero realmente son grafos, ya que, tienen propiedades en sus vértices (nodos) y enlaces, existiendo una teoría de grafos que respalda la representación causal de los datos de investigación.

Los DAG tampoco conforman un mapa mental de variables, las variables incluidas en la estructura causal no deben ser colocadas en cualquier orden y los enlaces entre las variables tampoco deben ser efectuados sin la revisión previa de evidencia científica.

Finalmente, un DAG no especifica el signo (positivo o negativo) de la relación entre una variable y otra, tampoco define la magnitud (grande o pequeña), el tipo (lineal o no lineal) y la forma. Es por ello que, el DAG es una herramienta no paramétrica, puesto que ninguna de las características mencionadas son mostradas en la estructura causal. El DAG solo es una representación de la probabilidad conjunta de las variables.

27.5 Teoría de grafos

En el siguiente grafo se observan 4 variables (A, B, C y D) unidas a través de líneas. A continuación, se profundizará sobre cada una de los componentes de un grafo.

27.5.1 Nodos

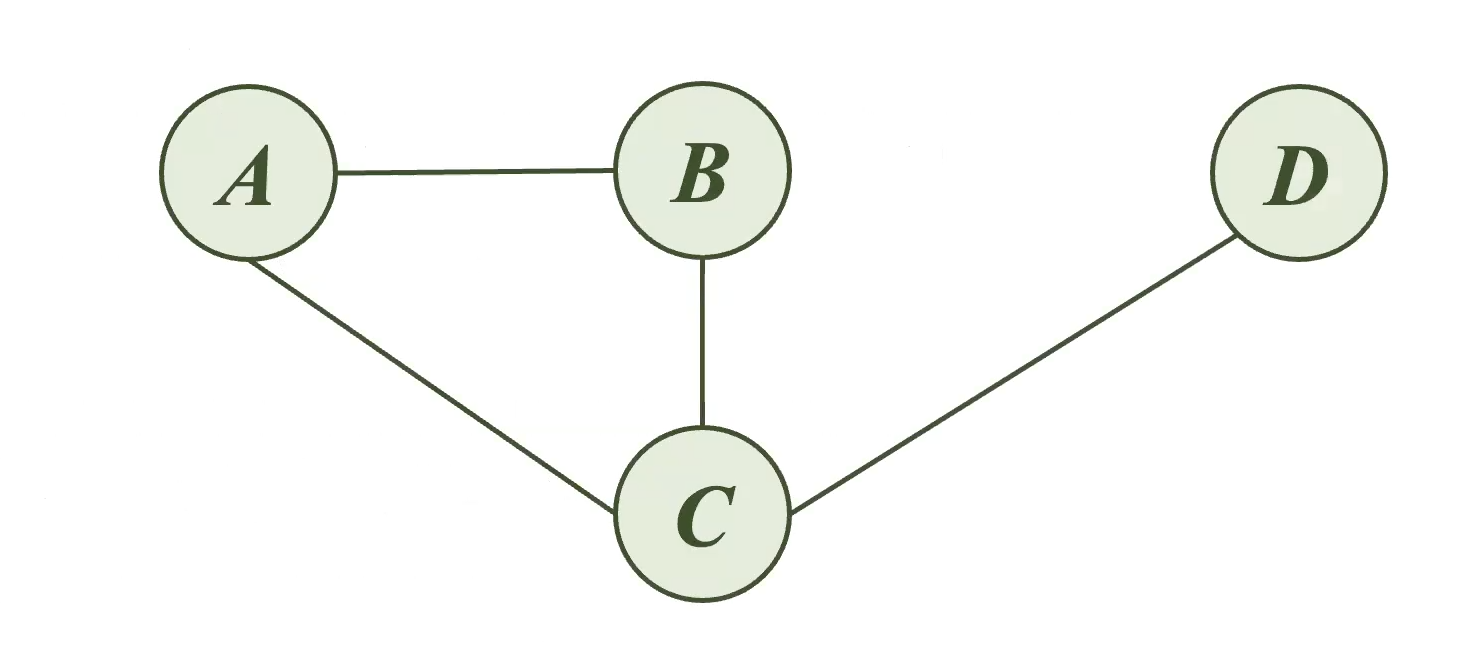
El primer elemento dentro de un grafo son los nodos o las variables.

En la siguiente figura, las variables A, B, C y D son los nodos.

27.5.2 Enlaces

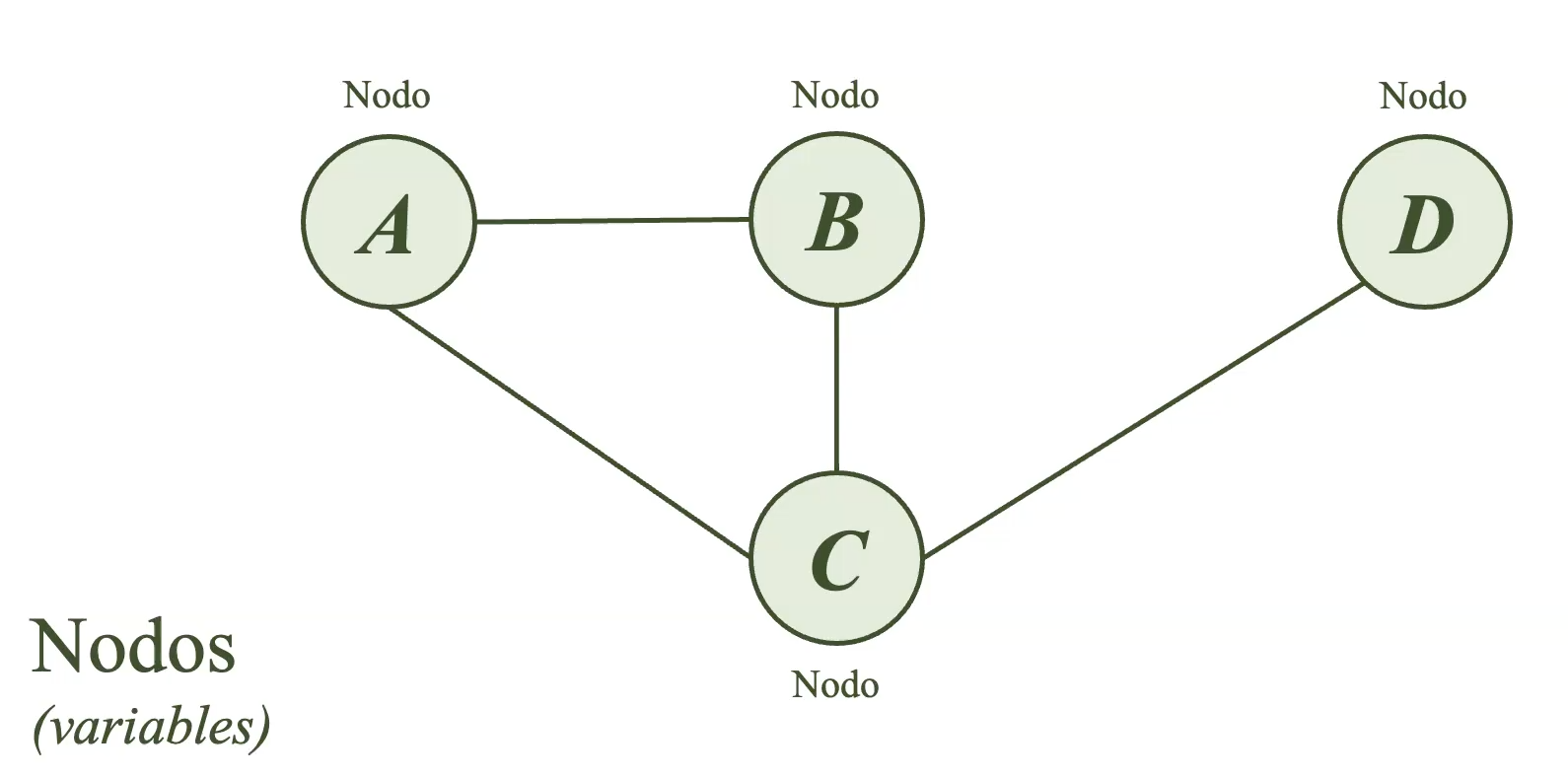
El segundo elemento de un grafo son los enlaces, los cuales representan un vínculo entre dos nodos.

La siguiente figura muestra vínculos entre las variables,

A y B
B y C
A y C
C y D

27.5.3 Grafo no dirigido

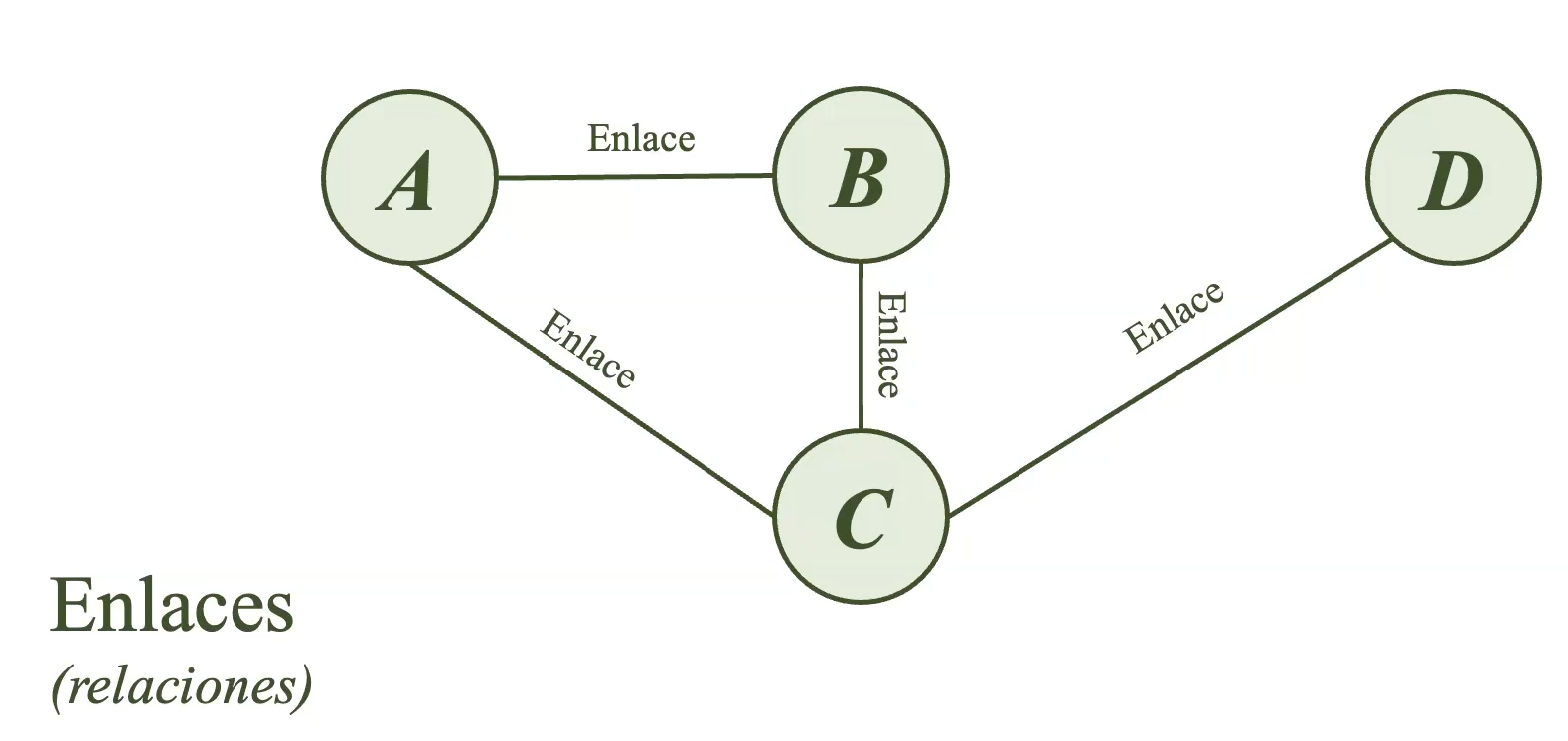
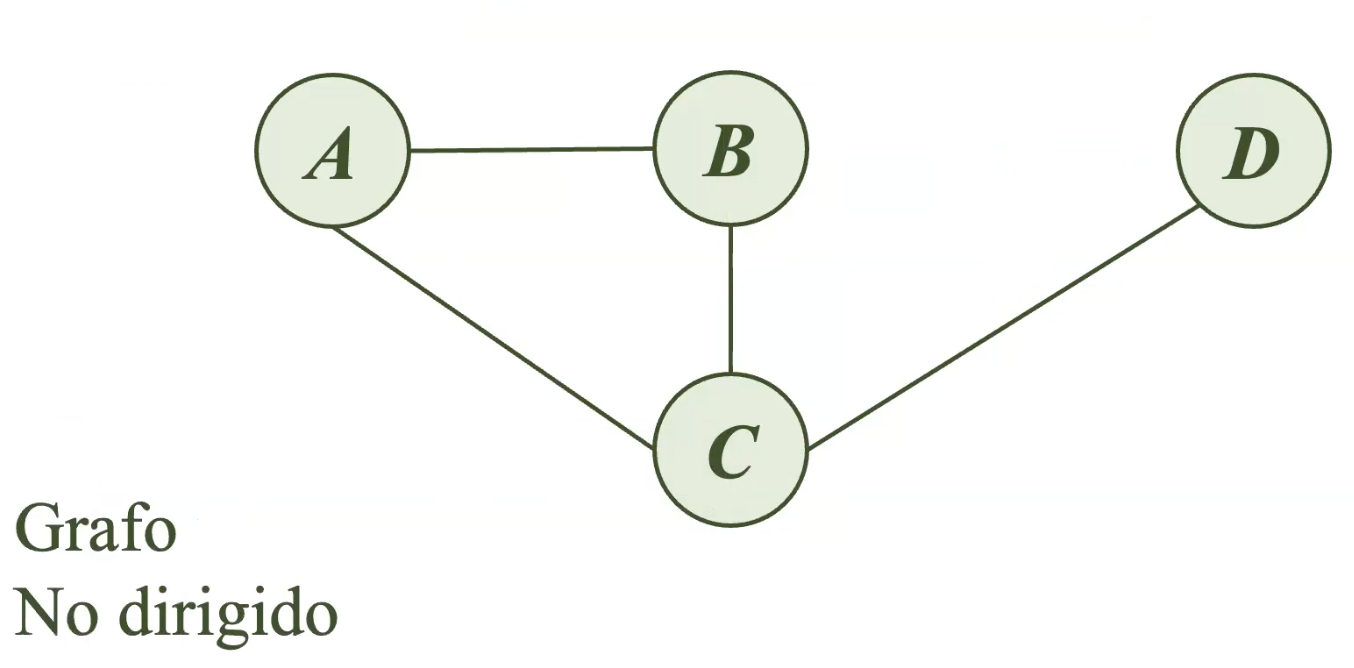
Los grafos que tienen enlaces sin una dirección específica entre las variables son conocidos como grafos no dirigidos. En estos casos, solo se sabe que A y B están relacionados, pero no es posible conocer si A influye en B o viceversa.

27.5.4 Grafo dirigido

Los grafos dirigidos, a diferencia de los no dirigidos, sí tienen enlaces que señalan una dirección entre los nodos. En estos casos, sí es posible identificar cuáles son las variables que influyen sobre otras. Por ejemplo, la variable A influye a las variables B y C, y esta relación es unidireccional.

27.5.5 Nodos adyacentes

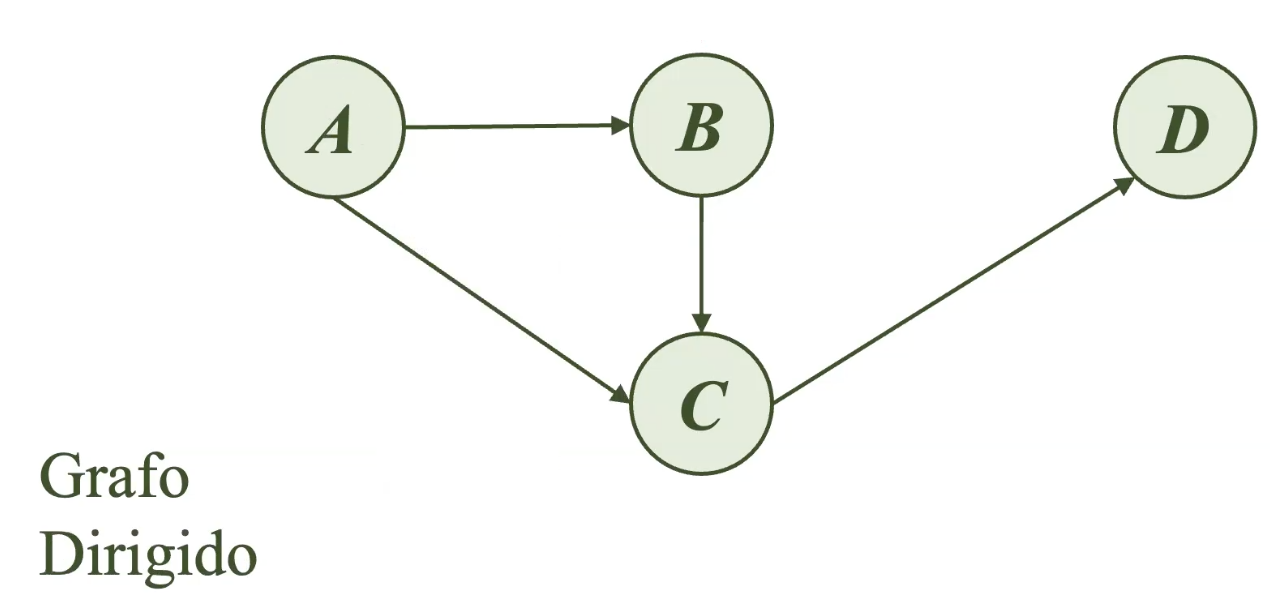
En la teoría de grafos, los nodos adyacentes son nodos que tienen una relación directa. Por ejemplo,

A y B
A y C
B y C
c y D

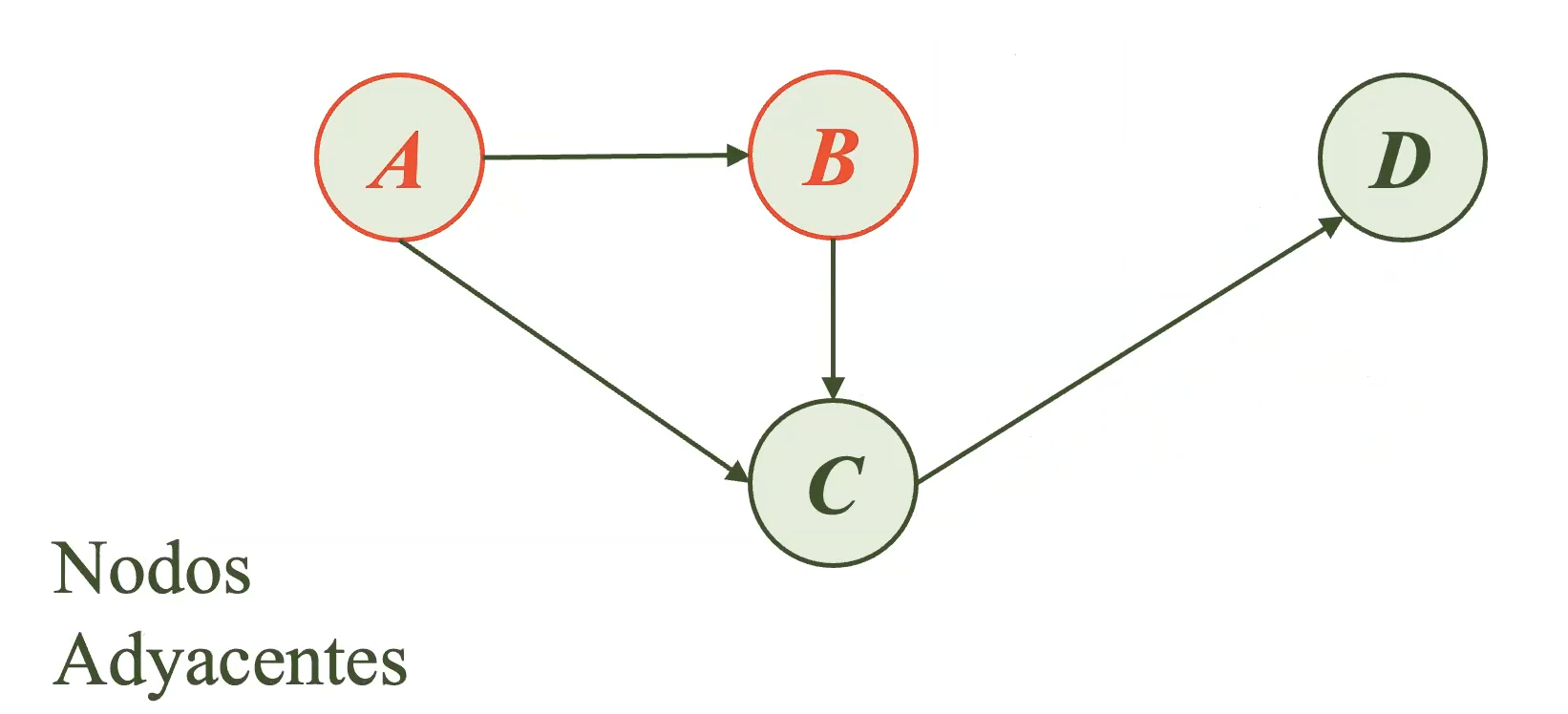
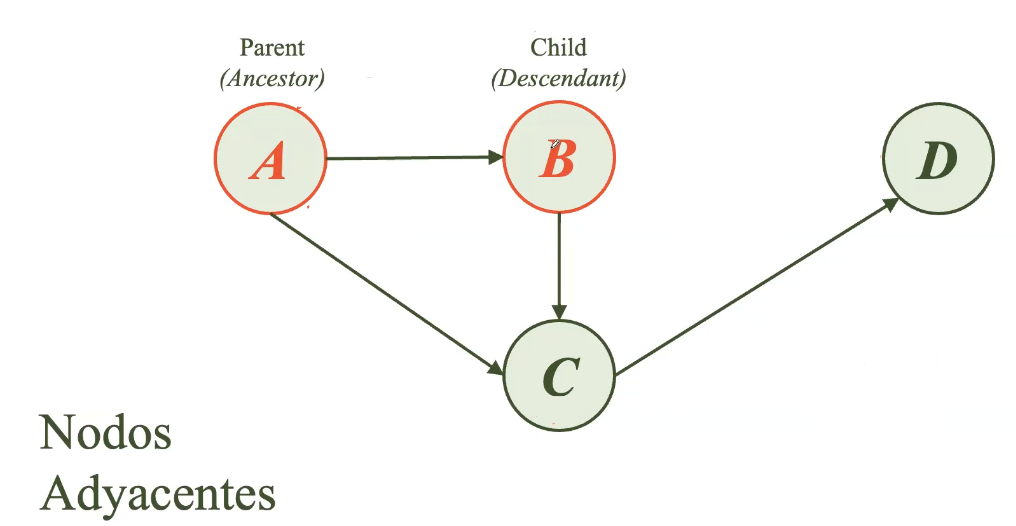
Existe una terminología específica para clasificar a los nodos adyacentes teniendo en cuenta si el enlace nace de un nodo o llega a uno. Por ejemplo, si el enlace llega a un nodo, este tendrá la clasificación de nodo hijo o descendiente (Nodo B, Figura 7). Por otro lado, si el enlace parte de un nodo, este será clasificado como nodo parental o ancestro (Nodo A de la siguiente figura).

27.5.6 Camino (Path)

Un camino o path se define como el recorrido existente entre un punto de origen y un punto de fin. Por ejemplo, si se desea llegar del nodo A al nodo D, uno de los caminos que se puede emplear es el siguiente: A -> C -> D.

27.5.6.1 Camino directo

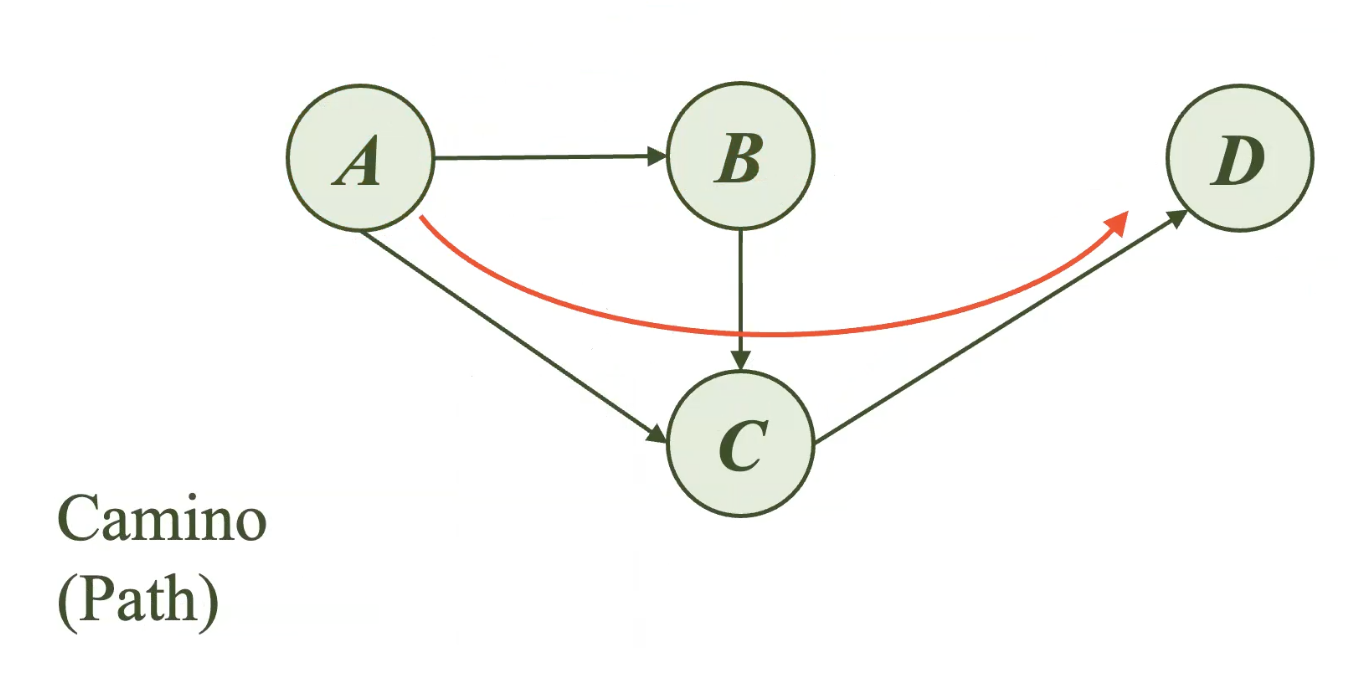
Los caminos directos son aquellos que no tienen nodos intermediarios.

Supongamos que se desea llegar del nodo A al nodo C. Al observar el siguiente grafo, es posible identificar dos caminos para cumplir con dicha tarea.

Camino 1: A -> B -> C
Camino 2: A -> C

Sin embargo, el camino 1, presenta un nodo intermediario (Nodo B), mientras que el camino 2 representa un camino directo entre el nodo A y el nodo C.

27.5.6.2 Camino indirecto

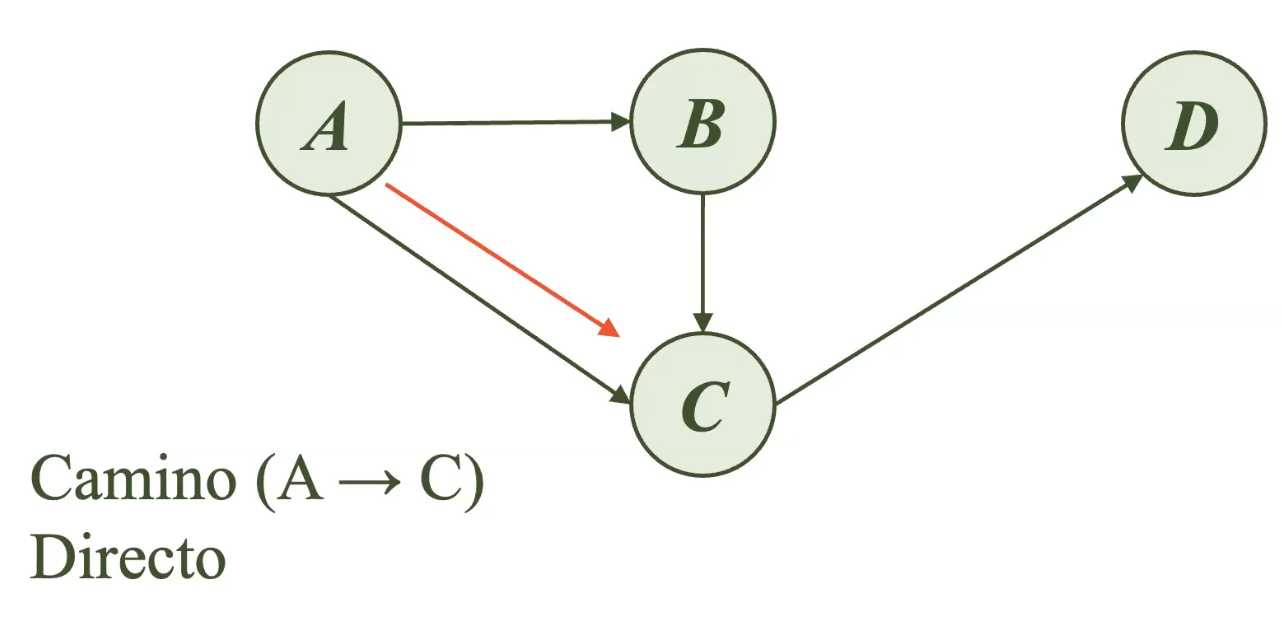
Por otro lado, los caminos indirectos son aquellos que sí incluyen a nodos intermediarios (Nodo B) entre en el punto de inicio y el punto de llegada.

27.6 DAGs

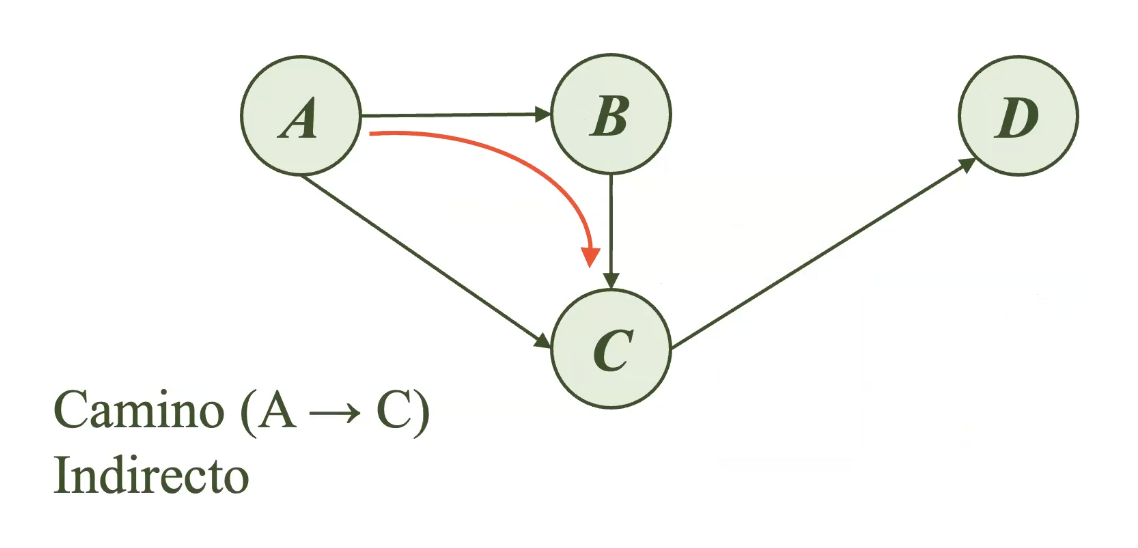
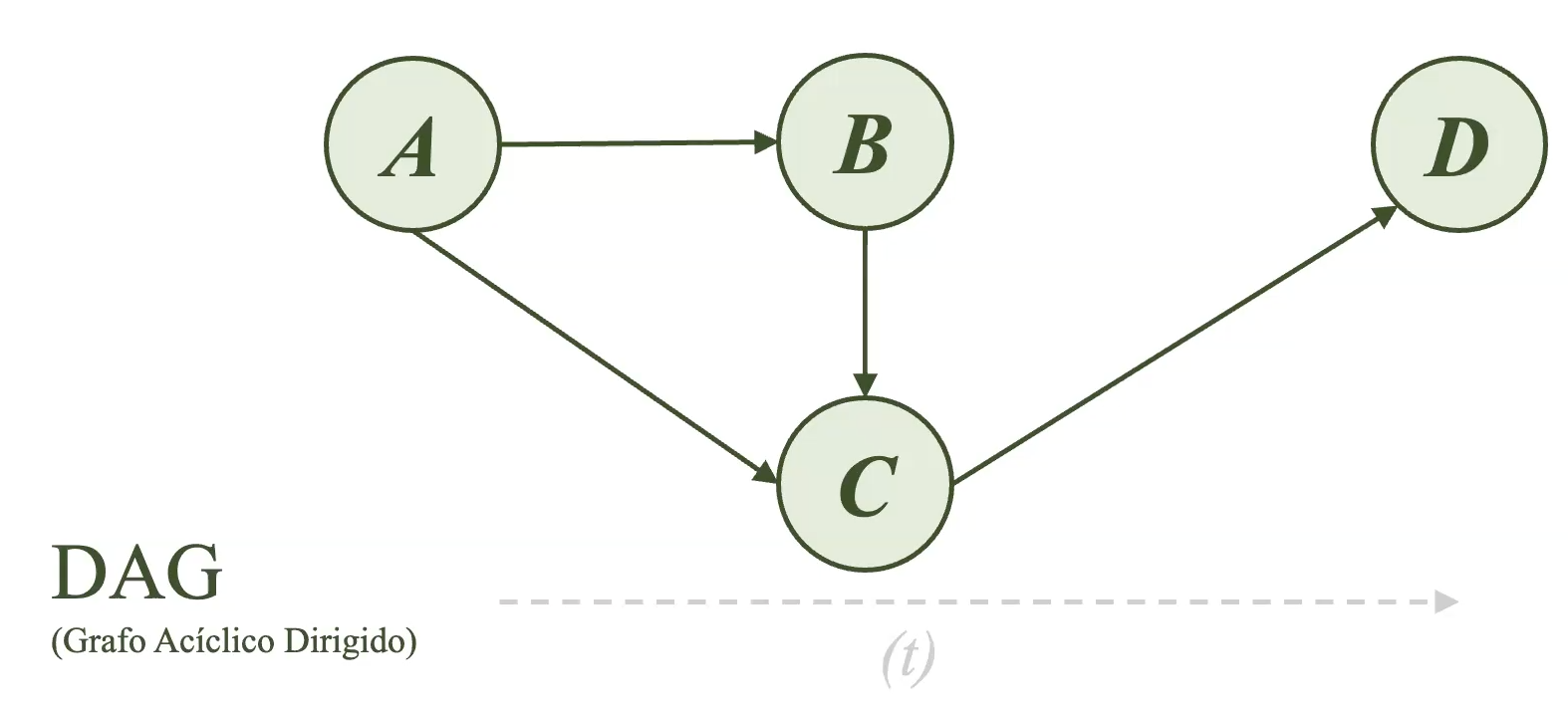
Un DAG es un grafo acíclico dirigido, que incluye también un componente de temporalidad, el cual es de suma importancia dentro del campo epidemiológico.

Por convención, el tiempo fluye de izquierda a derecha. Es por ello que, la temporalidad en un DAG se representa a través de la posición de los nodos. En la Figura 11, el nodo A ocurre antes que el nodo B, mientras que los nodos B y C ocurren al mismo tiempo. Además, los nodos B y C ocurren antes que el nodo D.

27.6.1 Bloques estructurales

Los bloques estructurales son unidades básicas dentro de los modelos basados en grafos como los DAG. La unidad mínima de un bloque estructural está compuesta por dos variables: un nodo parental o nodo ancestro y un nodo hijo o nodo descendiente.

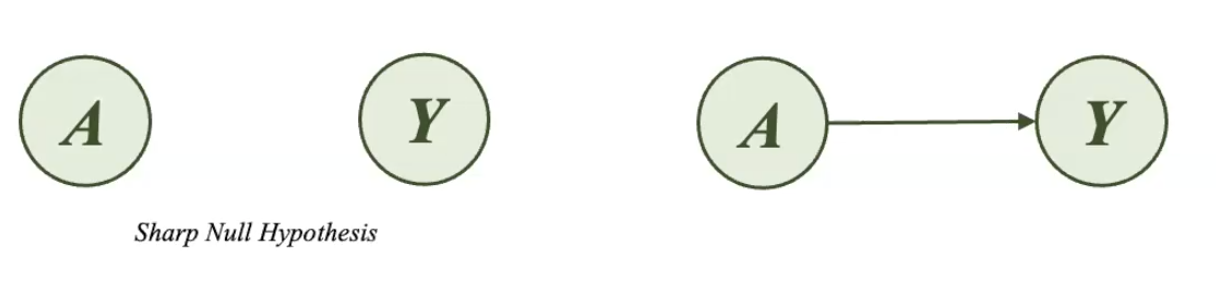
Teóricamente, se pueden presentar dos escenarios cuando elaboramos un DAG. El primer escenario supone la presencia de dos variables que pueden estar no vinculadas, mientras que el segundo escenario sí supone la vinculación de estas dos variables. Es decir, cuando solo dos variables están incluidas en un DAG, solo existirán dos bloques estructurales,

Bloque estructural sin enlace
Bloque estructural con enlace.

La presencia de una flecha apuntando de una variable a otra indica un efecto causal directo, es decir, no mediado por otra variable. También, indica que no se puede asumir que no existe efecto causal entre las variables.

Cuando se elabora un DAG, la asunción más potente de toda la teoría de DAG es la llamada Sharp Null Hypothesis, esta hipótesis plantea la ausencia de relación absoluta entre dos variables. Por tal motivo, si en un DAG se opta por no añadir una flecha entre dos variables, el investigador debe tener total seguridad de que esas variables científicamente no tienen ninguna vinculación. En cualquier otra circunstancia, se debería añadir la flecha para luego estimar las relaciones.

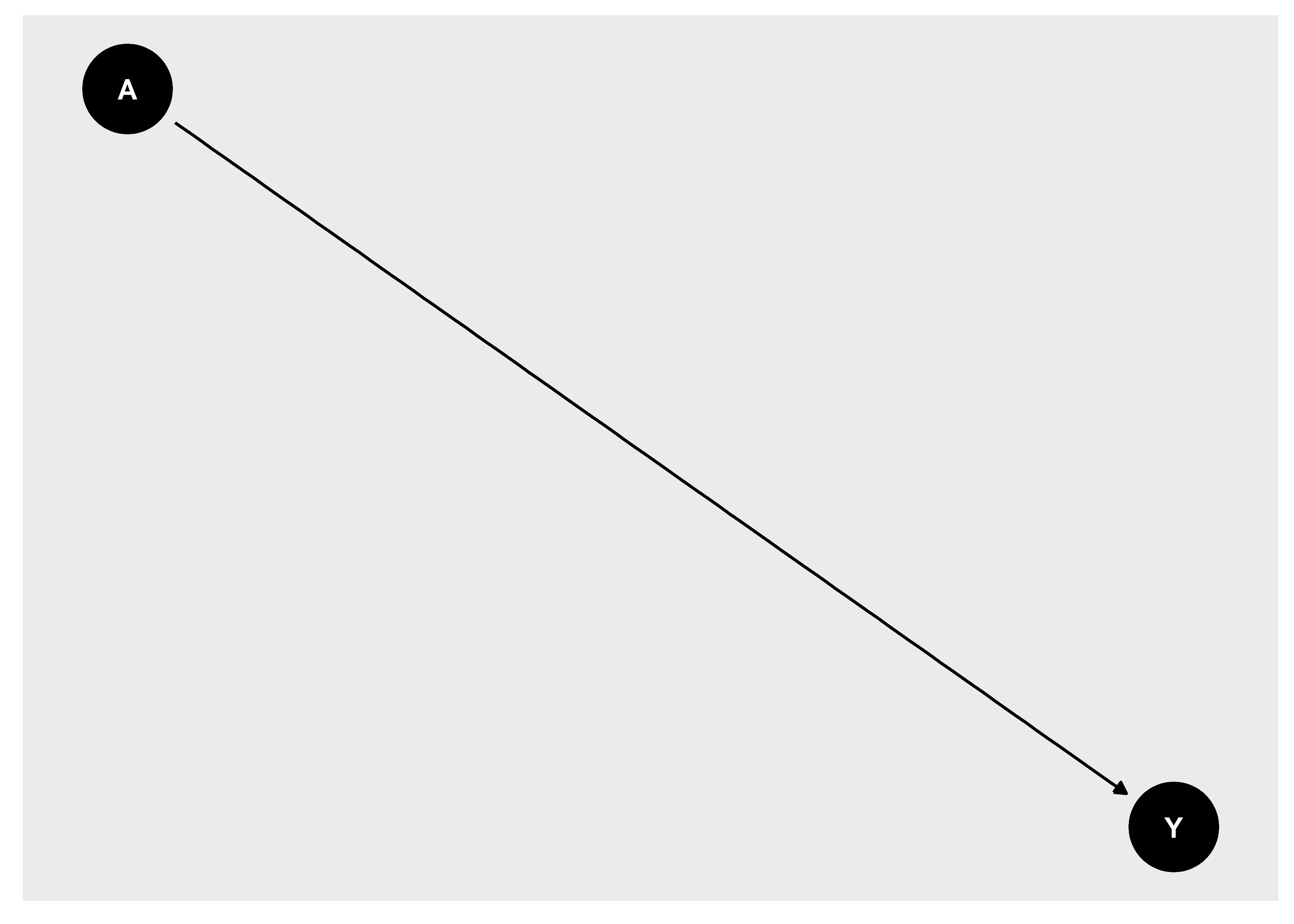
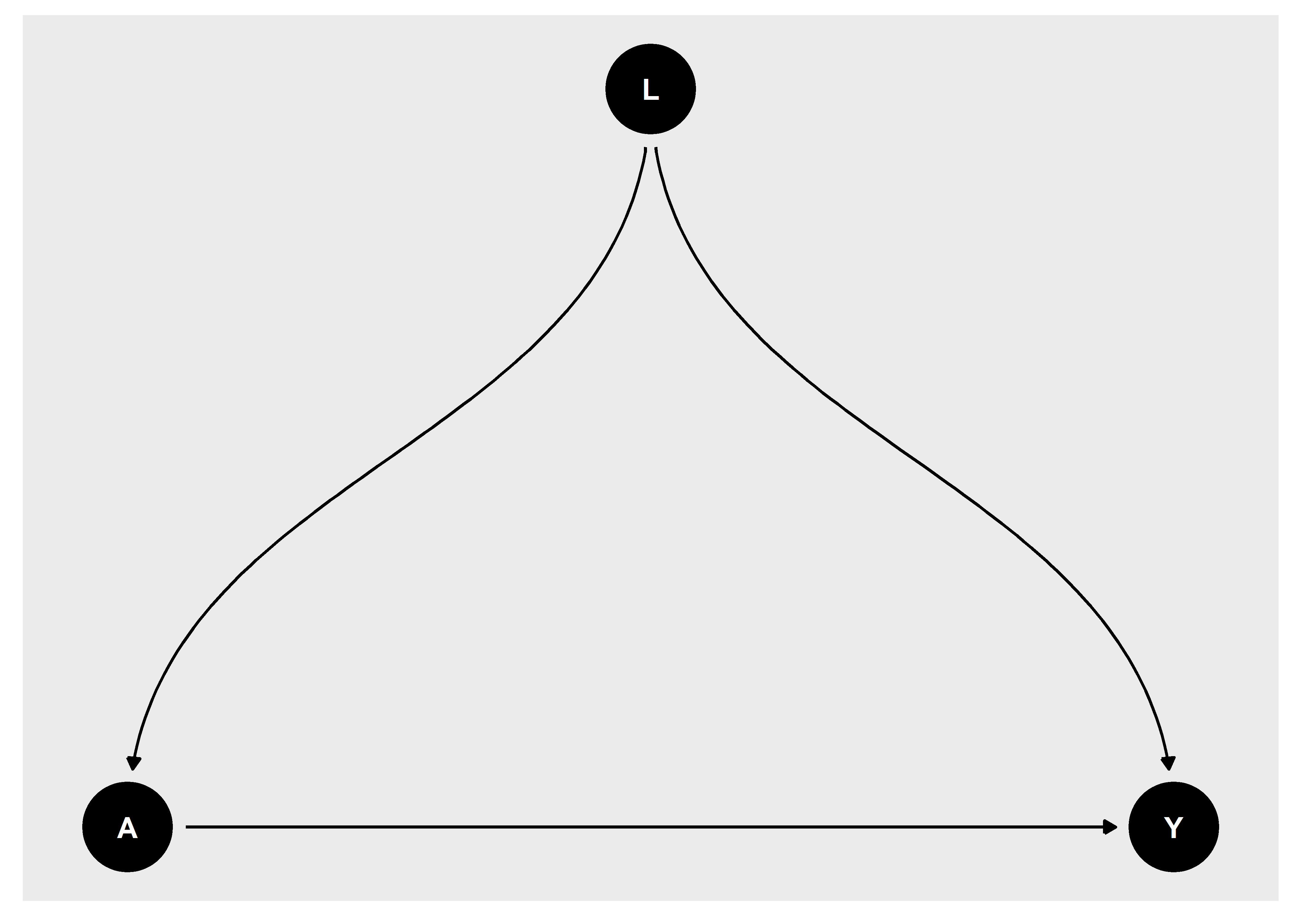
Cuando un bloque estructural tiene más de dos variables, pueden surgir más de dos escenarios a analizar. En la teoría de grafos, el primer bloque estructural es conocido como chain o bloque de tipo cadena. Este tipo de bloque estructural contiene una variable mediadora; en el ejemplo de la Figura 14, L es un nodo mediador en la relación existente entre A e Y. El segundo bloque estructural es conocido como Fork o bloque de tipo tenedor, este se caracteriza por tener una variable que es ancestro común de las otras dos variables. Por ejemplo, L es un ancestro común de A e Y. Finalmente, el tercer bloque estructural es concocido como immorality, ya que, el nodo descendiente (Nodo L) tiene dos nodos parentales (A e Y) que no están relacionados entre sí.

En el campo epidemiológico, a las cadenas se les conoce como variables mediadoras. En la Figura 14, L es una variable mediadora en la relación entre A e Y. las estructuras de tipo Fork también son llamadas variables confusoras. En este caso, L es una variable confusora entre A e Y. Finalmente, a los bloques de tipo immorality se les conoce como variables colisionadoras. Del mismo modo, L es una variable colisionadora en la relación entre A e Y.

27.6.2 Flujo de información

Nota

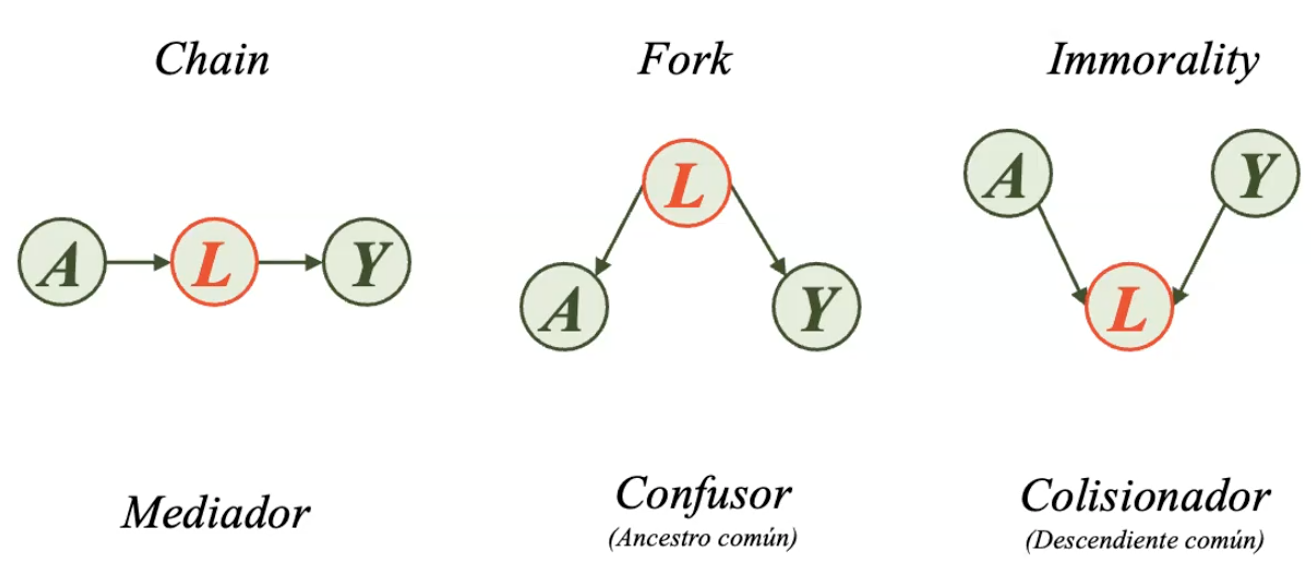
“La causalidad fluye en una dirección mientras que la información (estadística) fluye en ambas direcciones”

El proceso de flujo de información permite identificar si la información de una variable está contenida parcialmente en otra. Al establecer una relación entre dos variables a través de una flecha, se asegura que entre ellas existe dependencia. Por ejemplo, al existir dependencia entre las variables A y B, se puede afirmar que la información de Y está parcialmente contenida en A. Es decir, al saber información de A, se podría obtener también información de Y o viceversa. Sin embargo, lo que no se podría conocer con el flujo de información es si existirían modificaciones en Y a causa de una intervención sobre A.

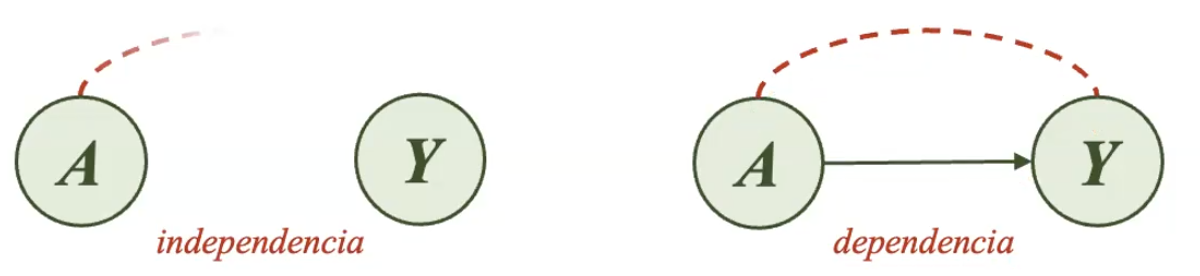
27.6.2.1 Flujo de información marginal

El flujo de información natural de tres o más variables sin la intervención de algún método estadístico o numérico es conocido como flujo de información marginal.

A continuación, se desarrollarán los tres tipos de escenarios que se pueden presentar al analizar la relación entre las variables A e Y.

El primer escenario es conocido como open path o camino abierto, este supone la dependencia entre las variables A e Y en presencia de una variable mediadora. Al no realizar ningún método estadístico sobre esta última variable, existirá un camino abierto de información en la relación analizada (A e Y).

Al no intervenir o controlar la variable confusora en la relación entre A e Y, también existirá flujo de información entre esas variables. Sin embargo, la información tendrá que ir en la dirección contraria a la flecha para cumplir con el flujo de información. Por ejemplo, en el grafo del medio de la Figura 16, la flecha debería nacer del nodo A y llegar al nodo L, y a partir de ahí, seguir su flujo hasta llegar a Y. Es por eso, que a este segundo escenario se le conoce como el escenario open backdoor path o de la puerta trasera abierta.

Finalmente, el tercer escenario supone no ajustar una variable colisionadora. En estos casos, se interrumpe el flujo de información entre A e Y, por lo tanto, existirá independencia entre dichas variables. Este escenario es conocido como blocked path o camino bloqueado.

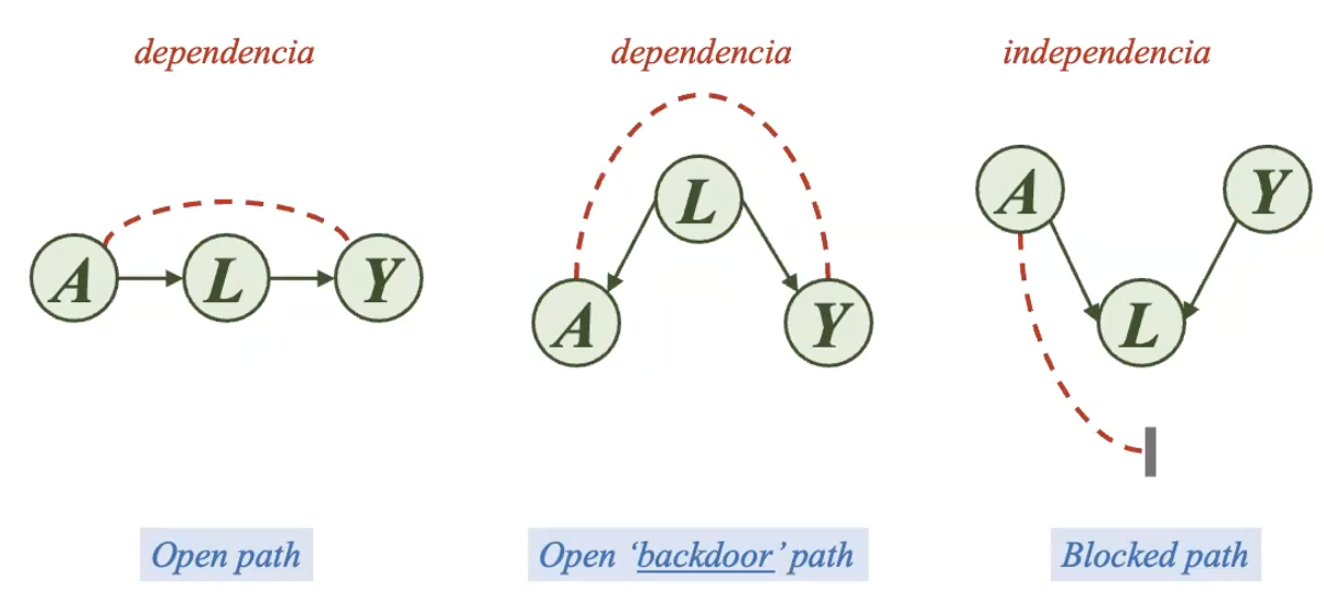
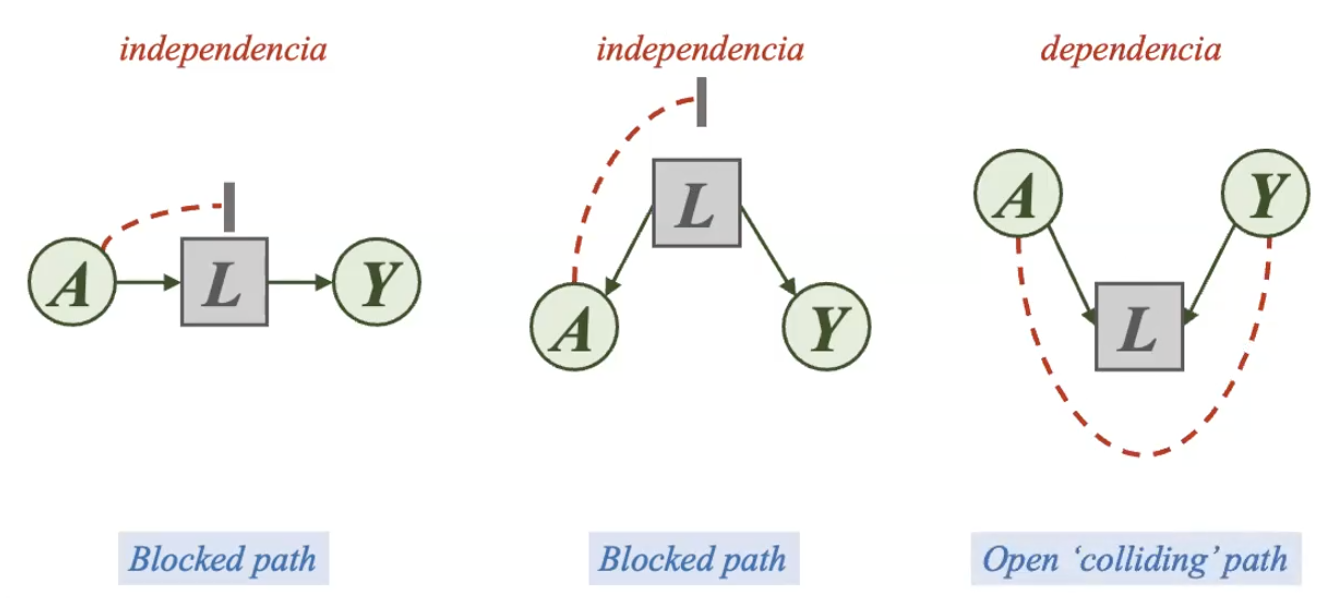
27.6.2.2 Flujo de información condicional

A diferencia del flujo de información marginal, el flujo condicional sí considera el ajuste estadístico sobre cada uno de los tipos de variables presentes en los bloques estructurales. Los resultados de ajustar cada una de estas variables están ilustradas en la figura 17 y serán explicadas a continuación.

Cuando una variable mediadora es ajustada, se interrumpe el flujo de información entre A e Y, convirtiéndolas en variables independientes, conformando así un escenario de camino bloqueado. Dado que estamos analizando dicha relación, y el único camino para que la información de A llegue a Y es a través de L, no se debería ajustar la variable mediadora.

Al ajustar una variable confusora, también estamos interrumpiendo el flujo de información entre A e Y. Sin embargo, esto es lo que se hace en muchos análisis epidemiológicos, se busca ajustar por confusores con el objetivo de eliminar el camino incorrecto creado por una variable que es un ancestro común de las dos variables que conforman la asociación de interés analizada.

Uno de los desafíos fundamentales al analizar la relación entre dos variables es la aparición del conocido open colliding path o camino abierto por el colisionador. Este fenómeno se origina debido al ajuste de una variable colisionadora y deja abierto un flujo de información que generaría sesgos en los resultados.

27.6.3 DAGs en R

Para la construcción de grafos acíclicos dirigidos (DAGs) en el ambiente de R podemos utilizar la función dagify del paquete ggdag para representar los bloques estructurales del DAG.

library(tidyverse)
library(ggdag)
theme_set(theme_dag_grey())

dagify(Y ~ A) %>%
  ggdag()

De la misma forma, podemos representar los bloques estructurales de tres nodos (variables) que revisamos anteriormente en el capítulo:

Mediador (Chain)

dagify(Y ~ L,
       L ~ A) %>%
  ggdag()

Confusor (Fork)

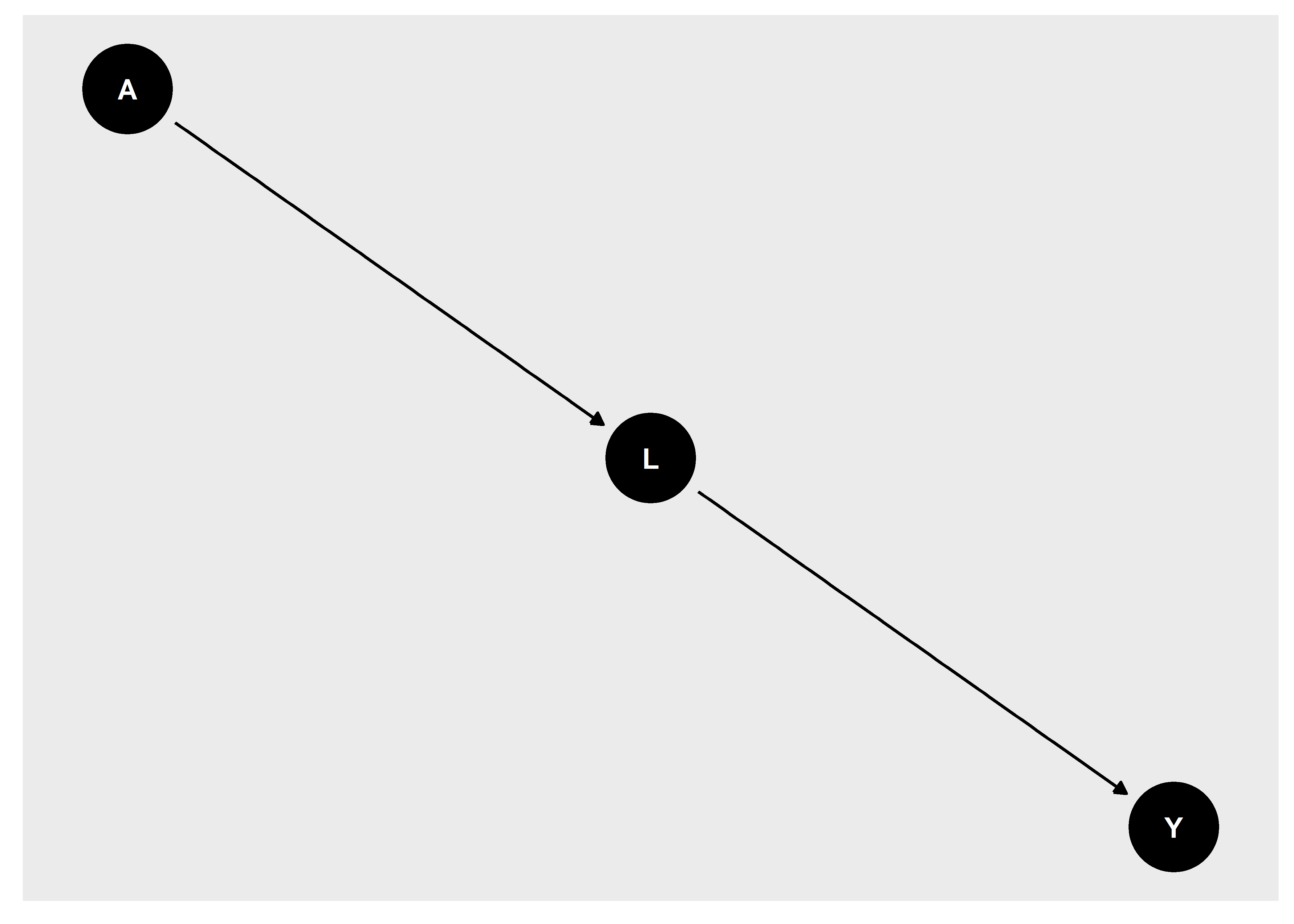
Ancestro Común

dagify(Y ~ L,
       A ~ L) %>%
  ggdag()

Colisionador (Immorality)

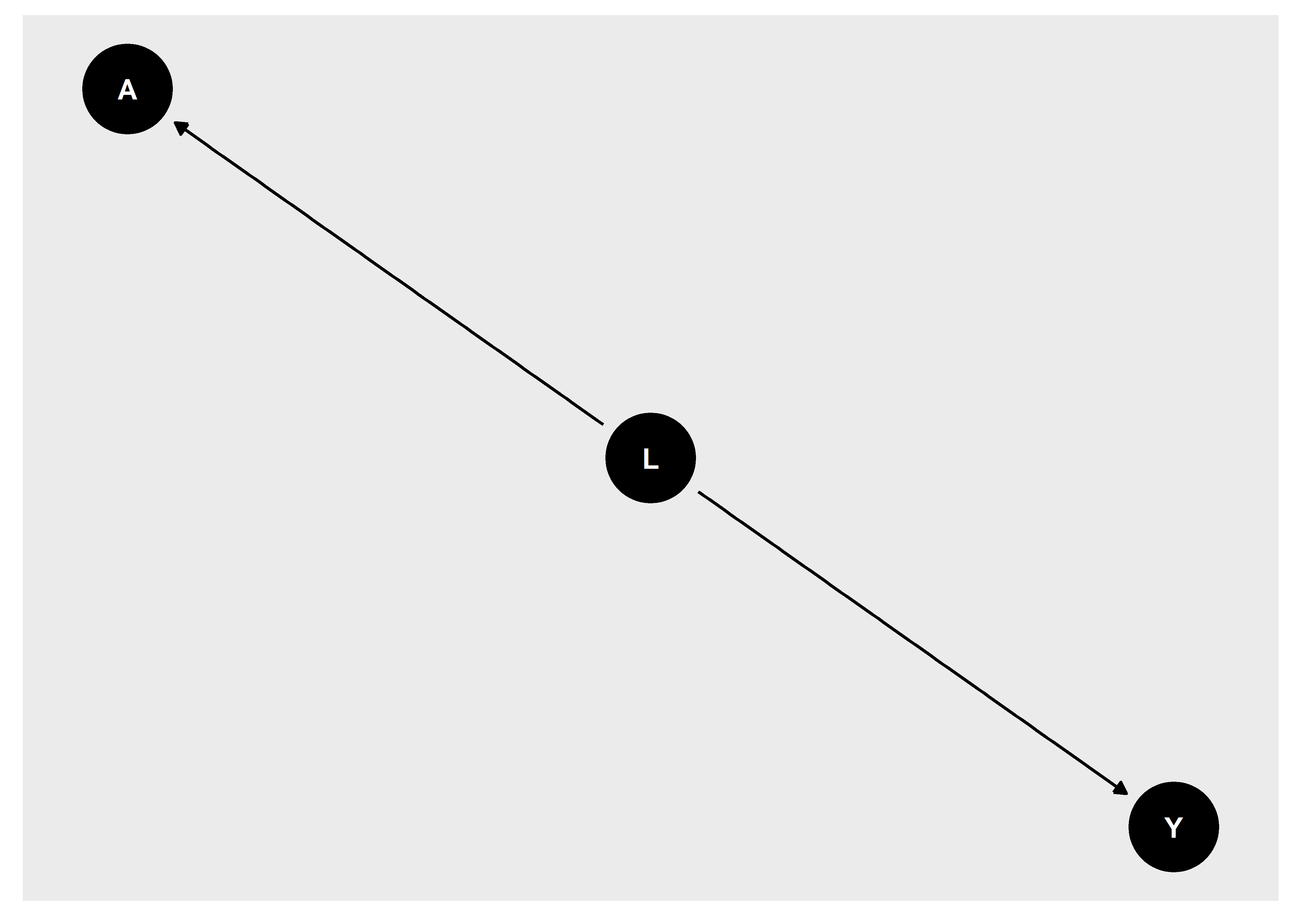
Descendiente Común

dagify(L ~ Y,
       L ~ A) %>%
  ggdag()

27.6.4 DAGitty en R

DAGitty es un entorno para crear, editar y analizar diagramas causales (también conocidos como grafos acíclicos dirigidos o redes bayesianas causales). La atención se centra en el uso de diagramas causales para minimizar el sesgo en estudios empíricos en epidemiología y otras disciplinas.

Esta plataforma puede usarse de forma independiente en un navegador web pero también tiene una inrefaz con R. dagitty es la librería en R que permite manejar los grafos y su procesamiento.

library(dagitty)

dag <- dagitty("dag{ A -> B; 
               C -> B; 
               A -> C; 
               D -> C; 
               E -> C; 
               F -> E; 
               F -> D; 
               G -> A; 
               G -> C; 
               E -> A; }")

plot(dag)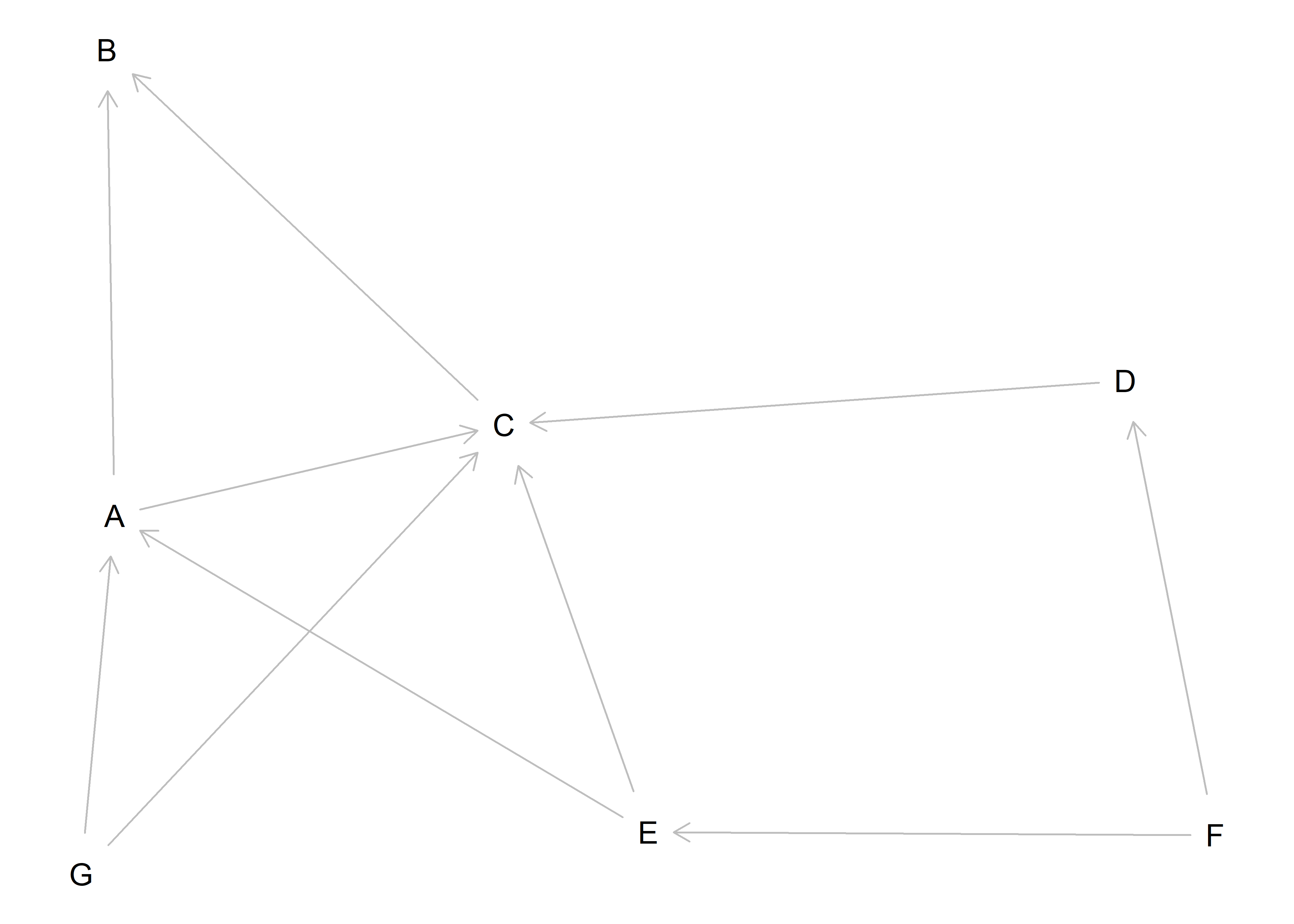

Al igual que en la contrucción de nuestros propios DAGs, también podemos usar el paquete ggdag para la representación visual de los grafos.

ggdag(dag)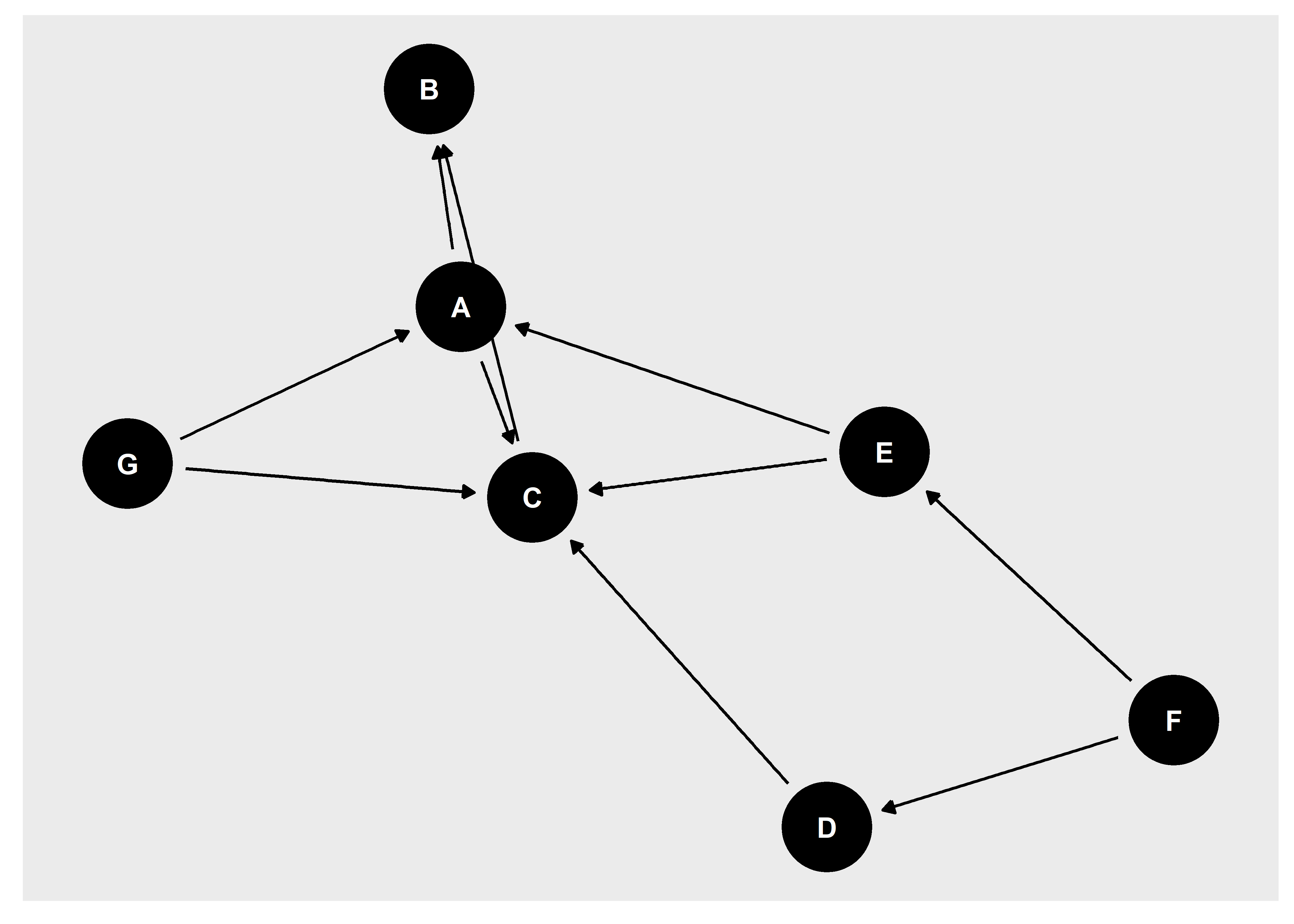

27.7 Set Mínimo de Ajuste (SMA)

La construcción de un DAG es una estrategia de identificación que responde a una pregunta de investigación bien definida. El set mínimo de ajuste (SMA), teóricamente, es el conjunto de variables que se deben considerar en el DAG para bloquear todos los caminos que no corresponden a la pregunta de investigación de interés.

En un modelo de regresión del desenlace, el SMA es el número mínimo de variables que se necesitan para cerrar todos los potenciales caminos (flujo de información) a excepción del camino causal principal (\(exposición \rightarrow desenlace\)).

dag1 <- dagify(Y ~ X1 + A + X2,
       X2 ~ A,
       A ~ X1) 

dag1 %>%
  ggdag()

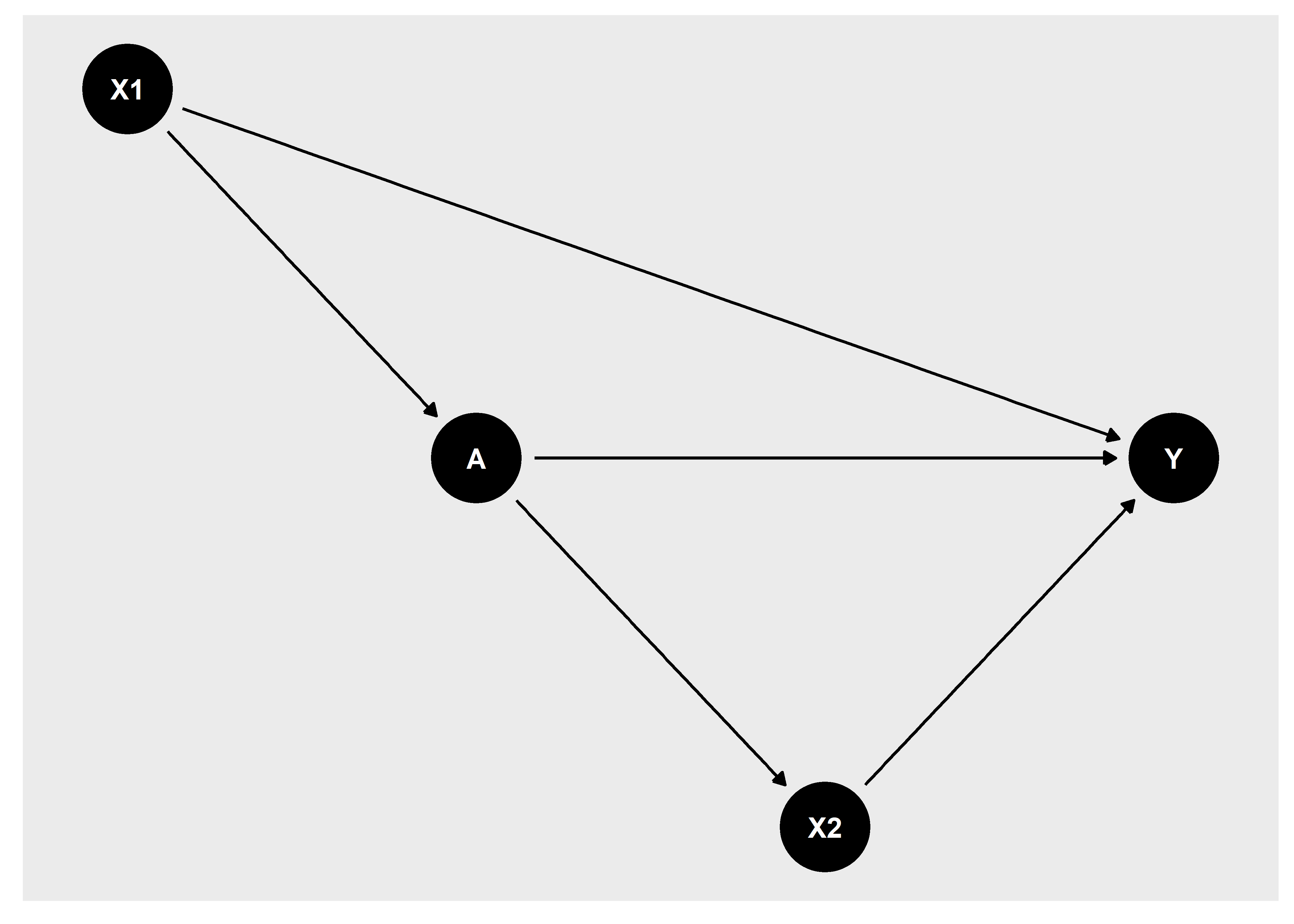
Lo primero que tenemos que definir en nuestro DAG es cual es la pregunta de investigación de interés definiendo la exposición (o tratamiento) y desenlace de interés.

dag1 <- dagify(Y ~ X1 + A + X2,
       X2 ~ A,
       A ~ X1,
       exposure = "A",
       outcome = "Y") 

ggdag_status(dag1)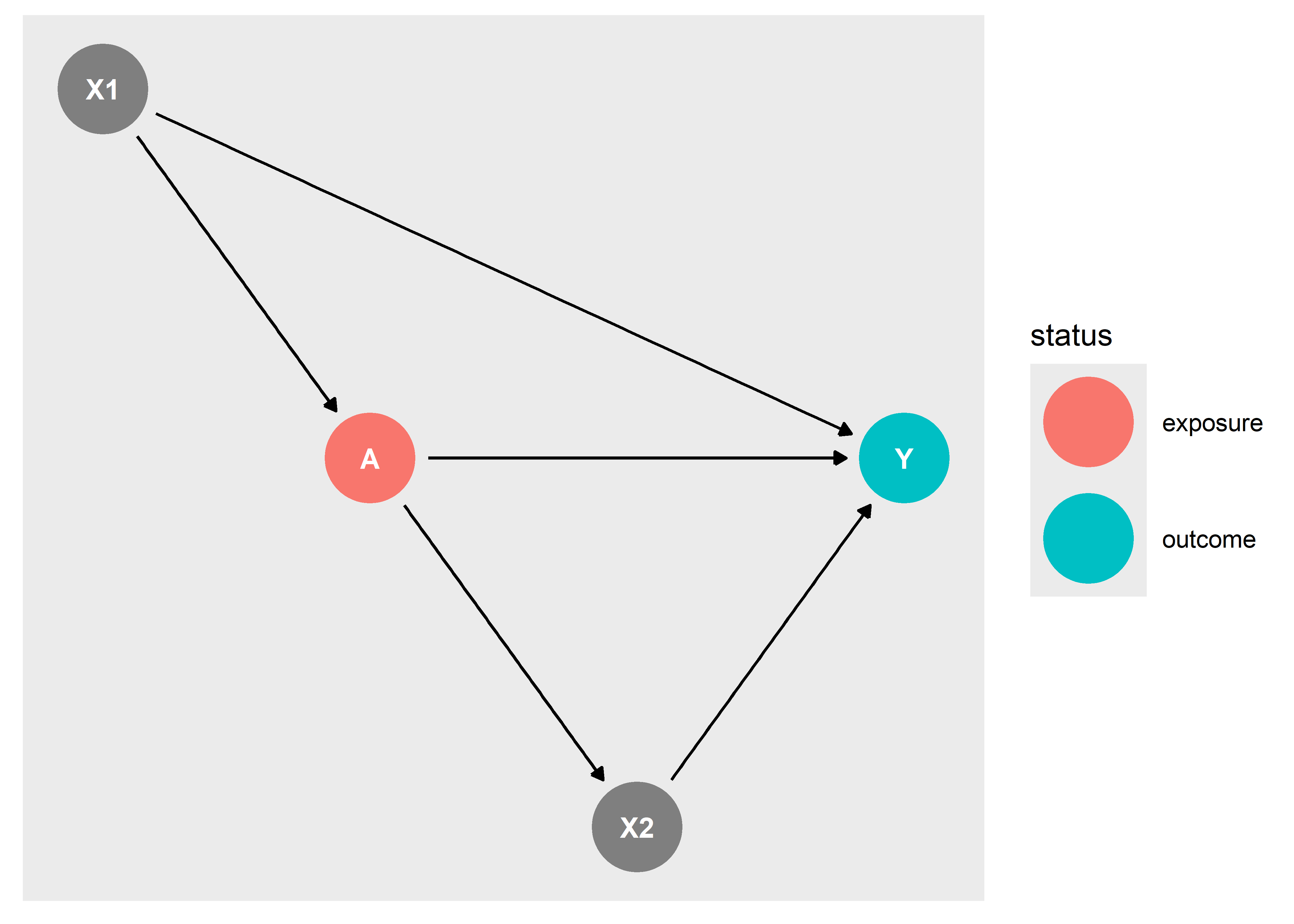

Identificamos todos los caminos (paths) abiertos entre nuestra exposición y desenlace de interés.

ggdag_paths(dag1, shadow = T)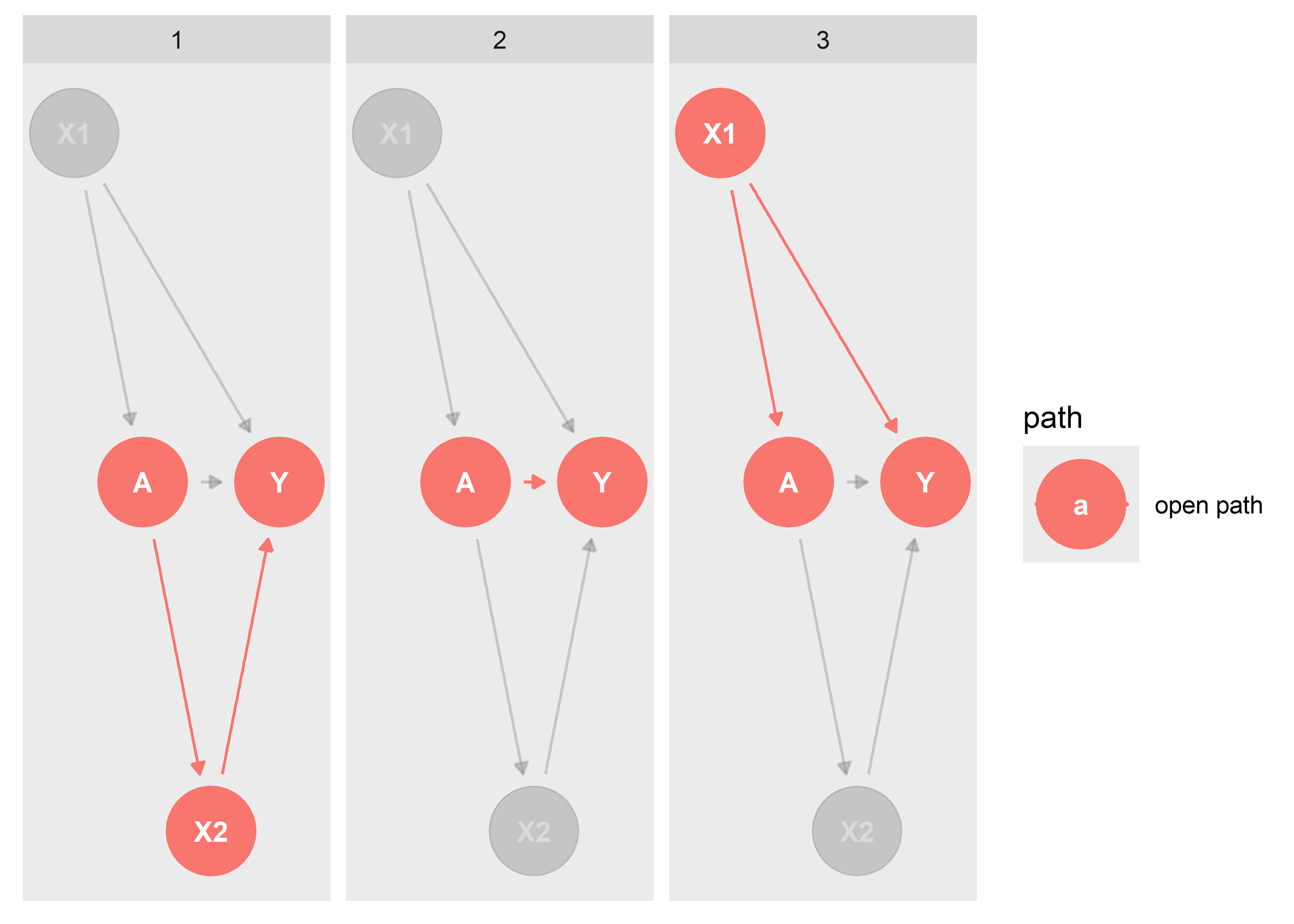

Bajo esta estructura causal (dag1), podemos identificar 2 tipos de efectos:

El Efecto Directo: El efecto exclusivo entre la exposición de interés y el desenlace de interés y que no contiene nigún bloque estructural entre ambos (ej. camino 2). En otras palabras, el efecto fluye únicamente por el enlace entre la exposición y desenlace de interés.
El Efecto Total: El efecto compuesto por todos los caminos que vinculan la exposición de interés y el desenlace de interés, excluyendo todos los backdoor paths (ej. camino 1 y 2). En otras palabras, es el efecto fluye a través de todos los enlaces y nodos descendientes que conectan la exposición y desenlace de interés.

En base a cual es el efecto causal de interés (Efecto Directo o Efecto Total), definiremos el set mínimo de ajuste.

Primero identificamos el SMA para determinar el Efecto Directo:

ggdag_adjustment_set(dag1, shadow = T, effect = "direct")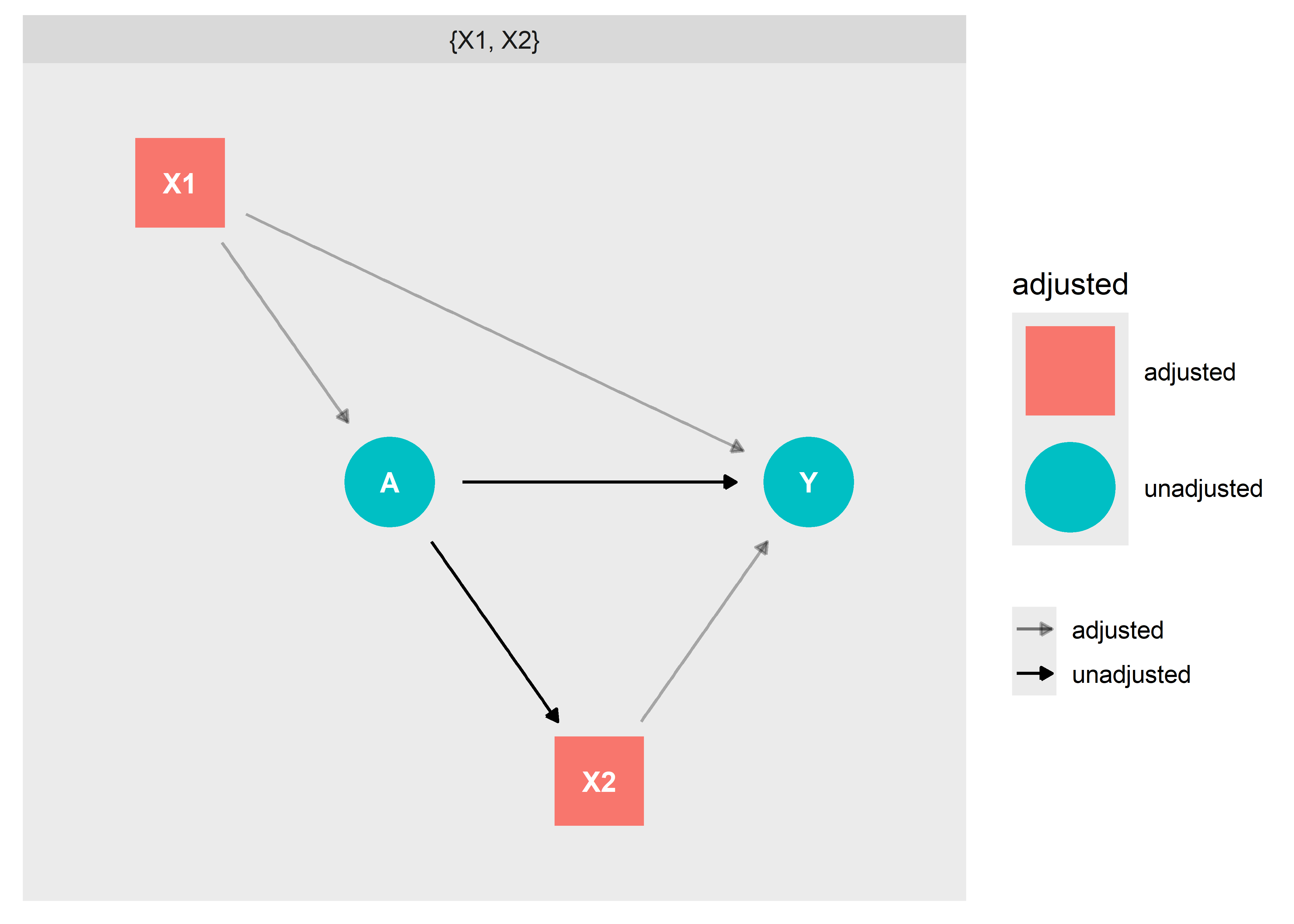

En base a estos resultados, concluimos que el SMA para determinar el efecto directo de A en Y se necesita ajustar por las variables \(X_1\) y \(X_2\).

Ahora, identificamos el SMA para determinar el Efecto Total:

ggdag_adjustment_set(dag1, shadow = T, effect = "total")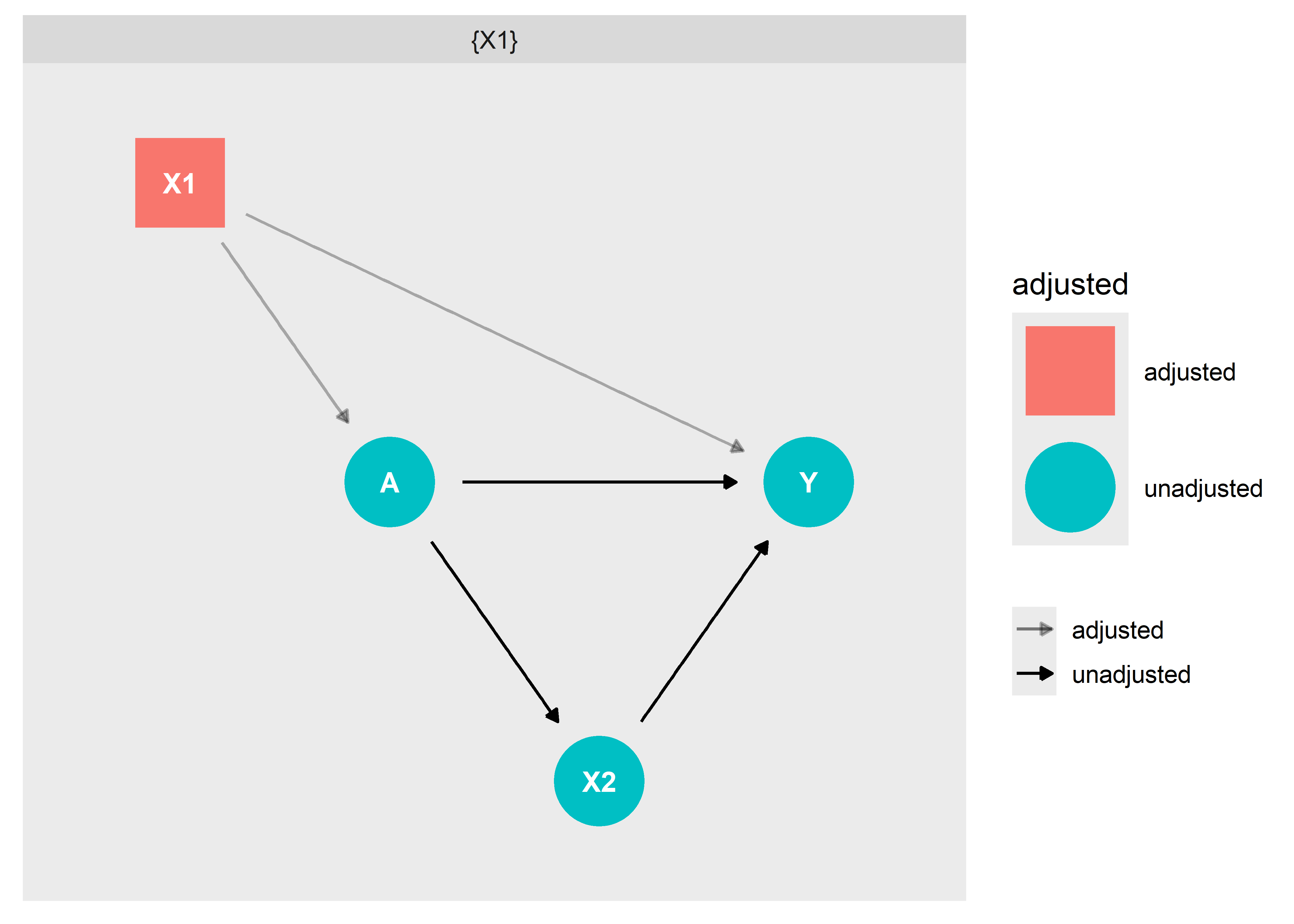

En base a estos resultados, concluimos que el SMA para determinar el efecto total de A en Y se necesita solo ajustar por \(X_1\).

Es importante hacer énfasis en que la definición del SMA depende de la pregunta de investigación de interés. Si esta pregunta cambia, el SMA también cambiará. A continuación un ejemplo del cambio en el SMA si ahora nos interesa el efecto directo de la variable \(X_1\) en \(Y\).

ggdag_adjustment_set(dag1, shadow = T, effect = "direct", exposure = "X1")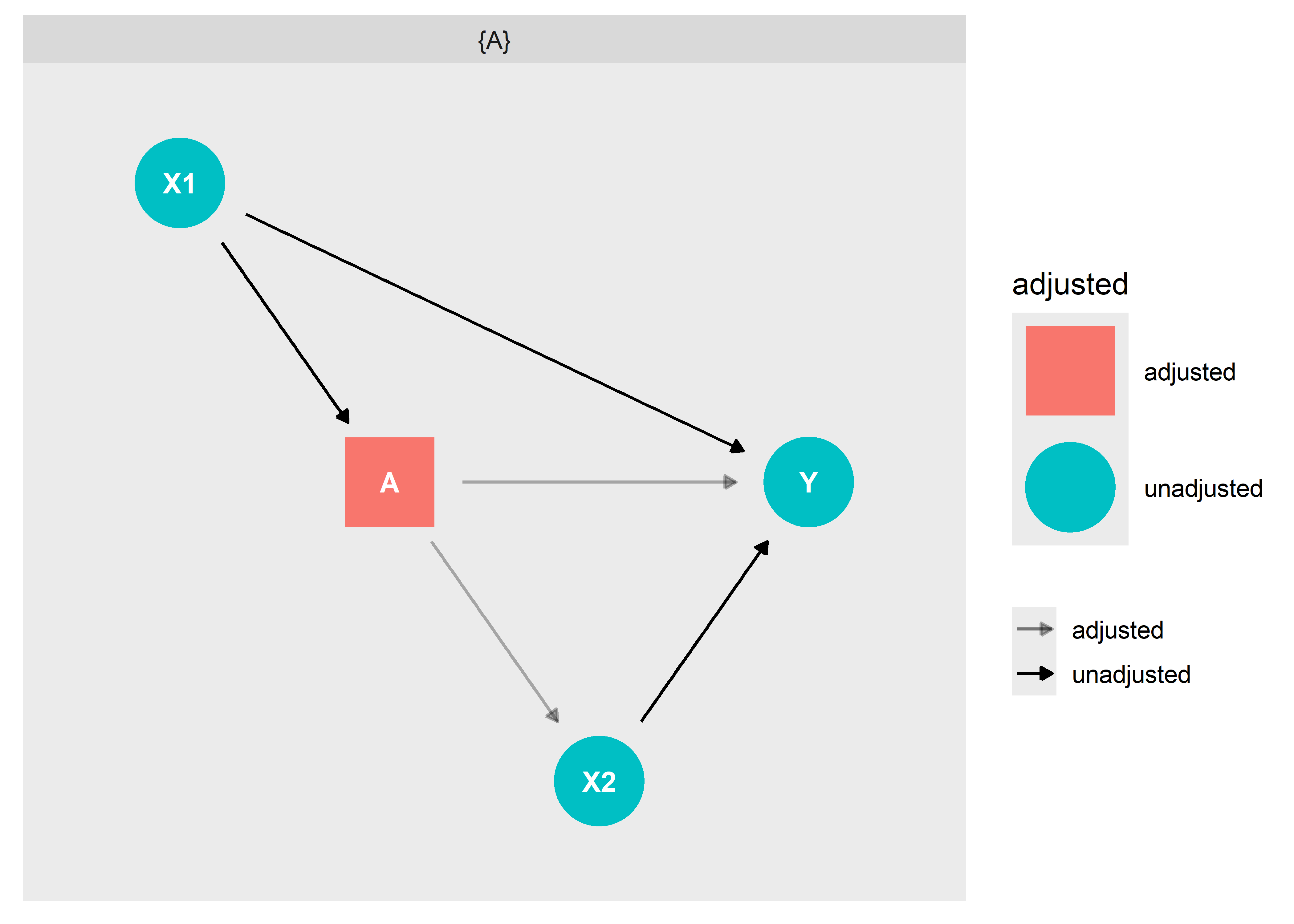

Incluso, si intentamos identificar el efecto total de \(X_1\) en \(Y\) no necesitamos ajustar por ninguna variable.

ggdag_adjustment_set(dag1, shadow = T, effect = "total", exposure = "X1")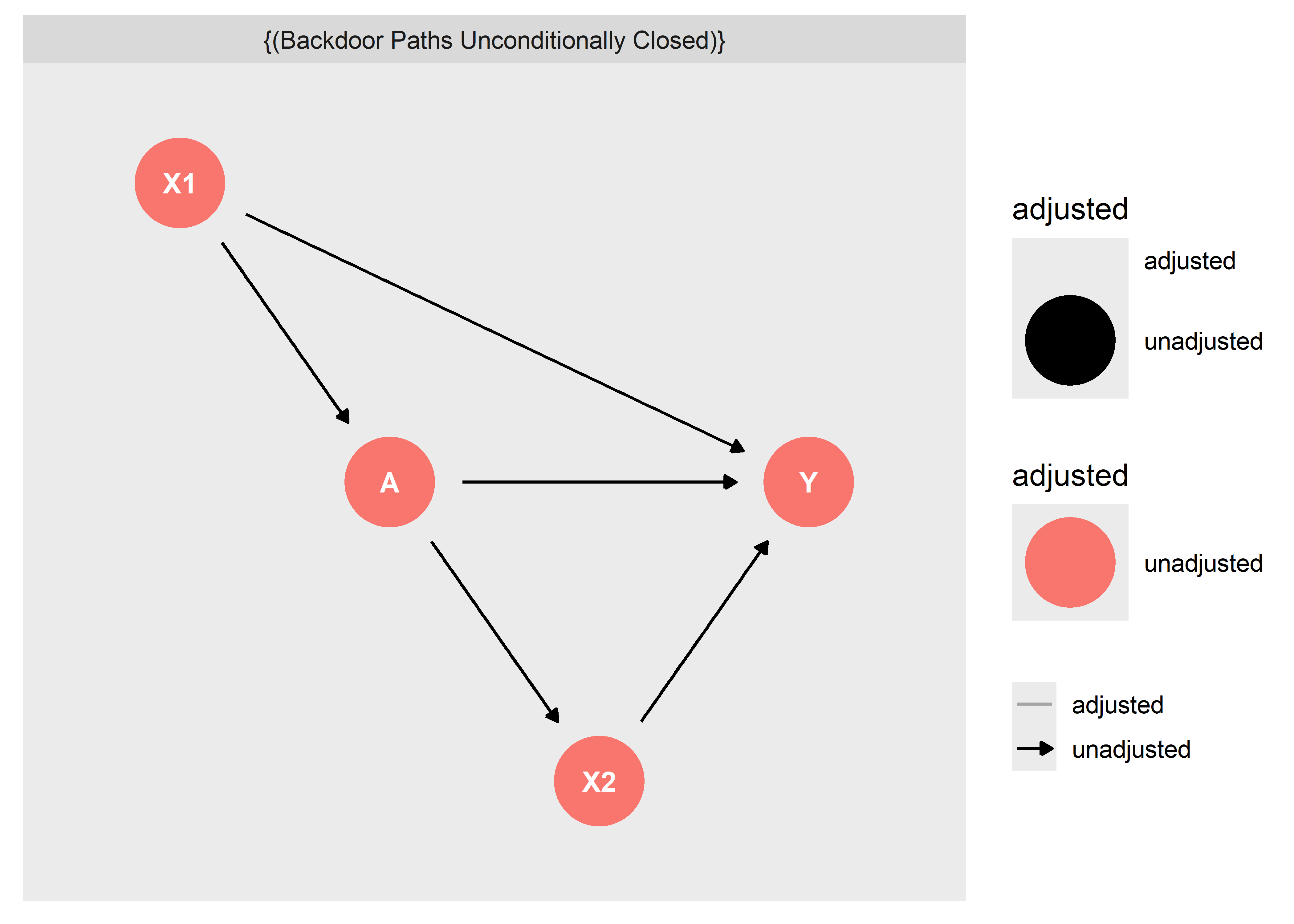

Esta diferencia es muy importante en la literatura biomédica y se encuentra definido como la falacia de la tabla 2.

Falacia de la tabla 2

En el contexto de la presentación de los coeficientes que provienen de modelos de regresión múltiple, existe el error de interpretar cada coeficiente como “el efecto de la variable \(X_i\) en la variable \(Y\), ajustado por todas las otras variables en el modelo”. Como hemos visto anteriormente, al cambiar la variable de exposición, también cambia el set mínimo de ajuste para identificar el efecto total o directo.

Por lo tanto, al usar el mismo DAG, la interpretación de todos los coeficientes del modelo en algunos casos hará referencia al efecto directo, en otros al efecto total y en algunos casos a conclusiones incorrectas dado que podemos estar “ajustando” por variables que no debieron ajustarse, como colisionadores (Westreich & Greenland).

27.7.1 Versiones múltiples de SMA

En estructuras más complejas, es posible determinar múltiples versiones de SMA. Por ejemplo el siguiente dag2:

dag2 <- dagify(Y ~ X1 + A + X2 + X4,
       X2 ~ A,
       A ~ X1 + X3,
       X4 ~ X3,
       exposure = "A",
       outcome = "Y") 

dag2 %>%
  ggdag()

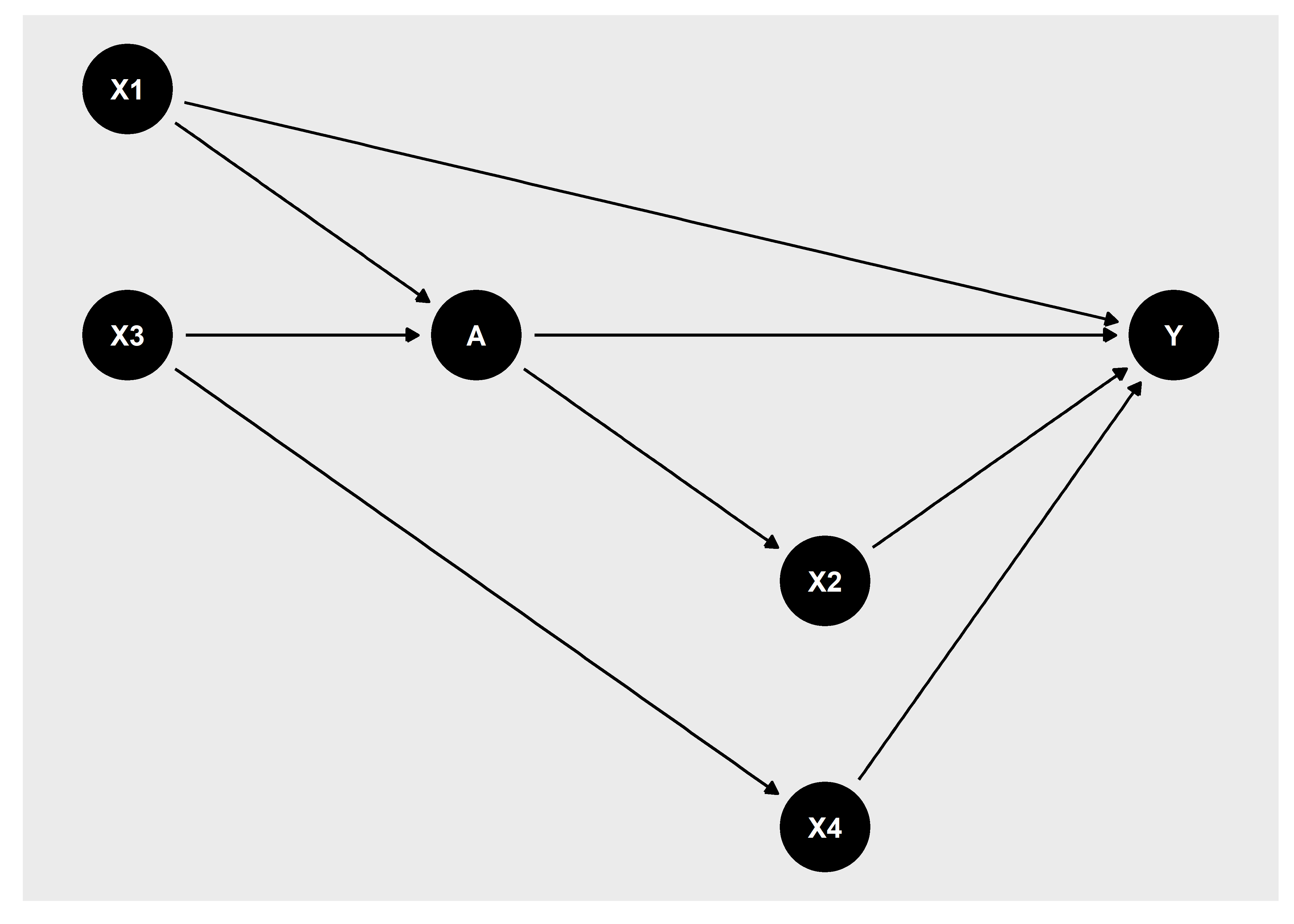
Observamos que existe una mayor cantidad de variables confusoras en la relación entre \(A \rightarrow Y\), como son \(X_1\) y \(X_3\). También tenemos una variable mediadora, \(X_2\):

ggdag_paths(dag2, shadow = T)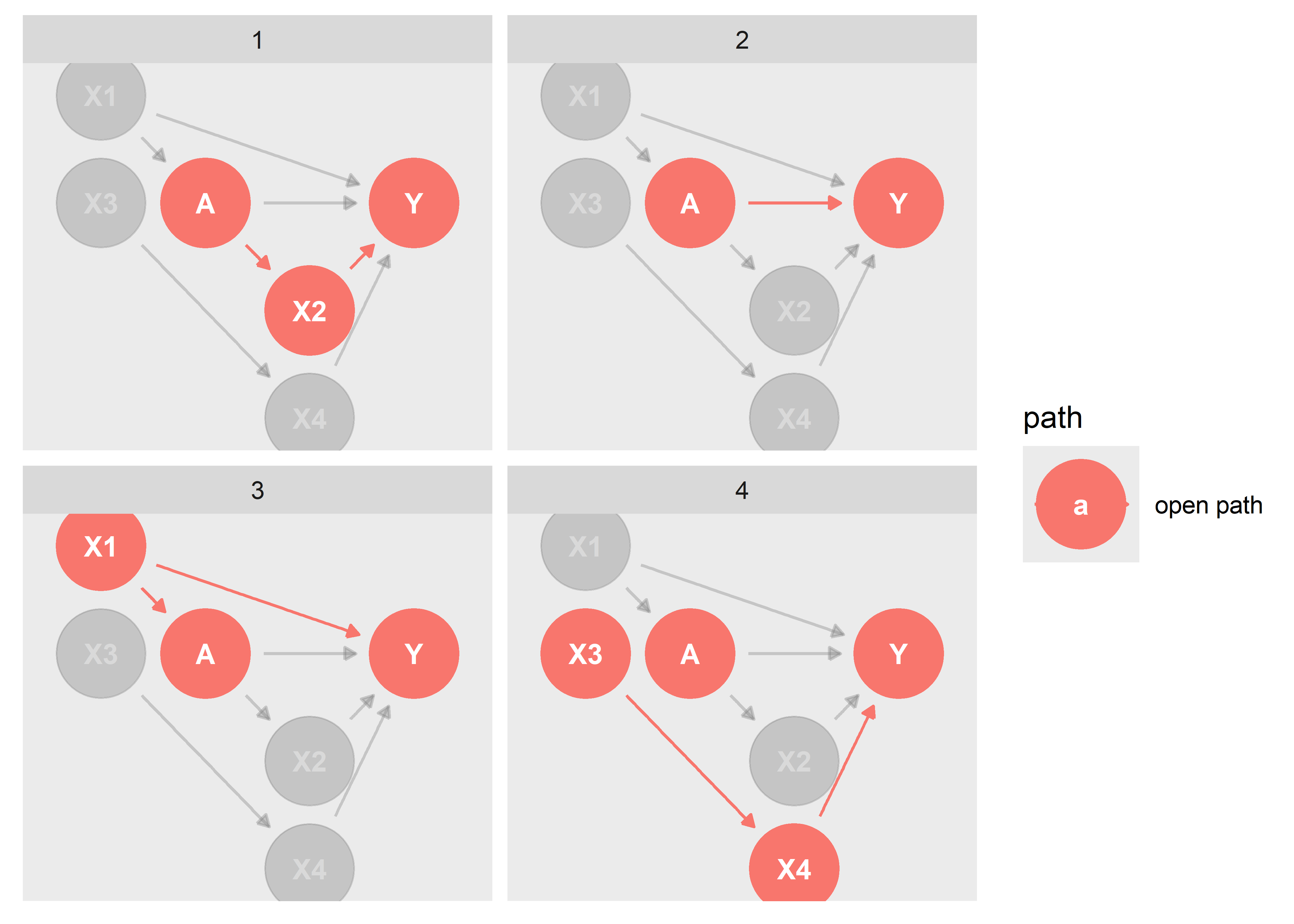

Con esta nueva estructura causal tenemos 2 SMA para determinar el efecto directo:

ggdag_adjustment_set(dag2, shadow = T, effect = "direct")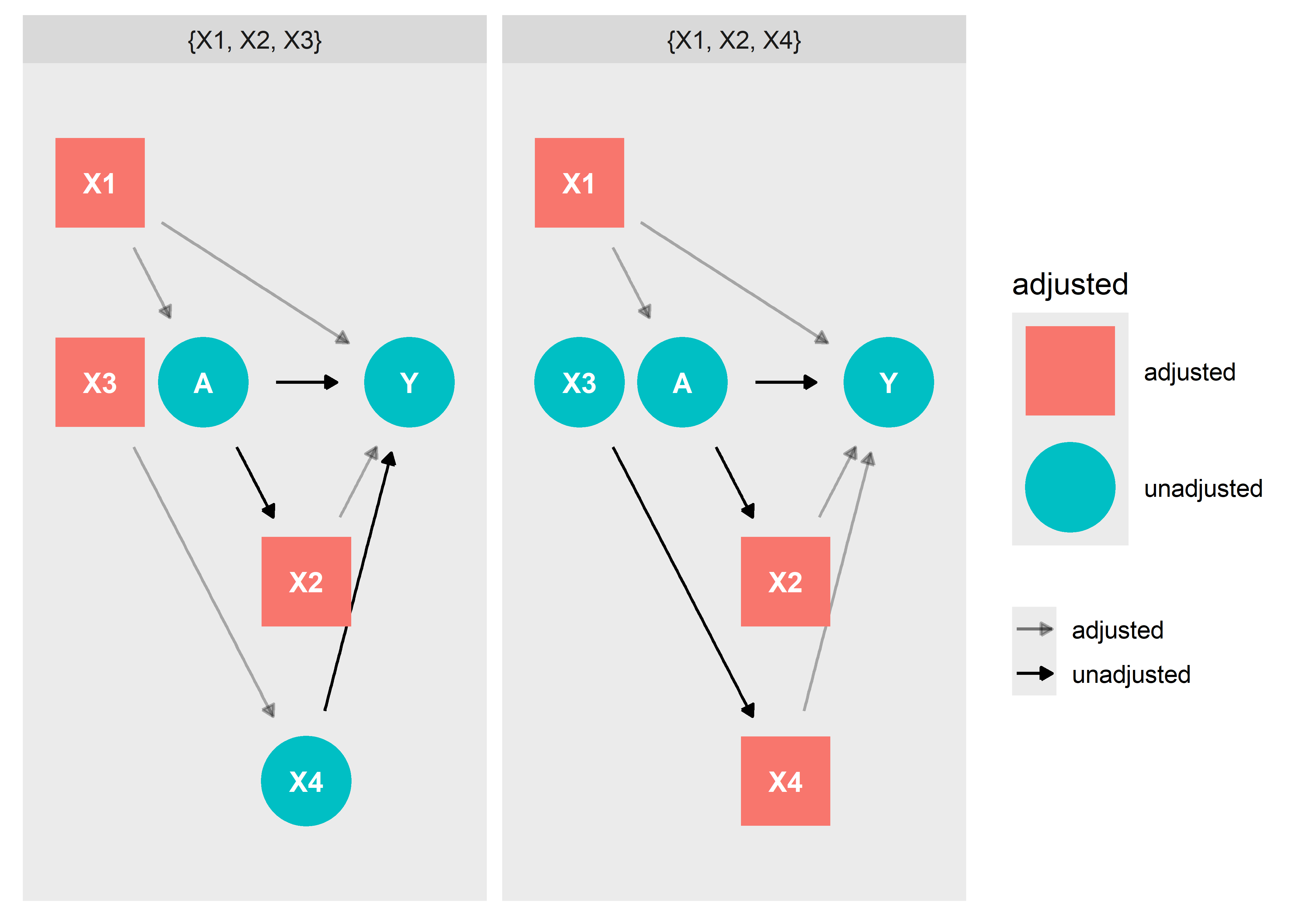

Y 2 SMA para determinar el efecto total:

ggdag_adjustment_set(dag2, shadow = T, effect = "total")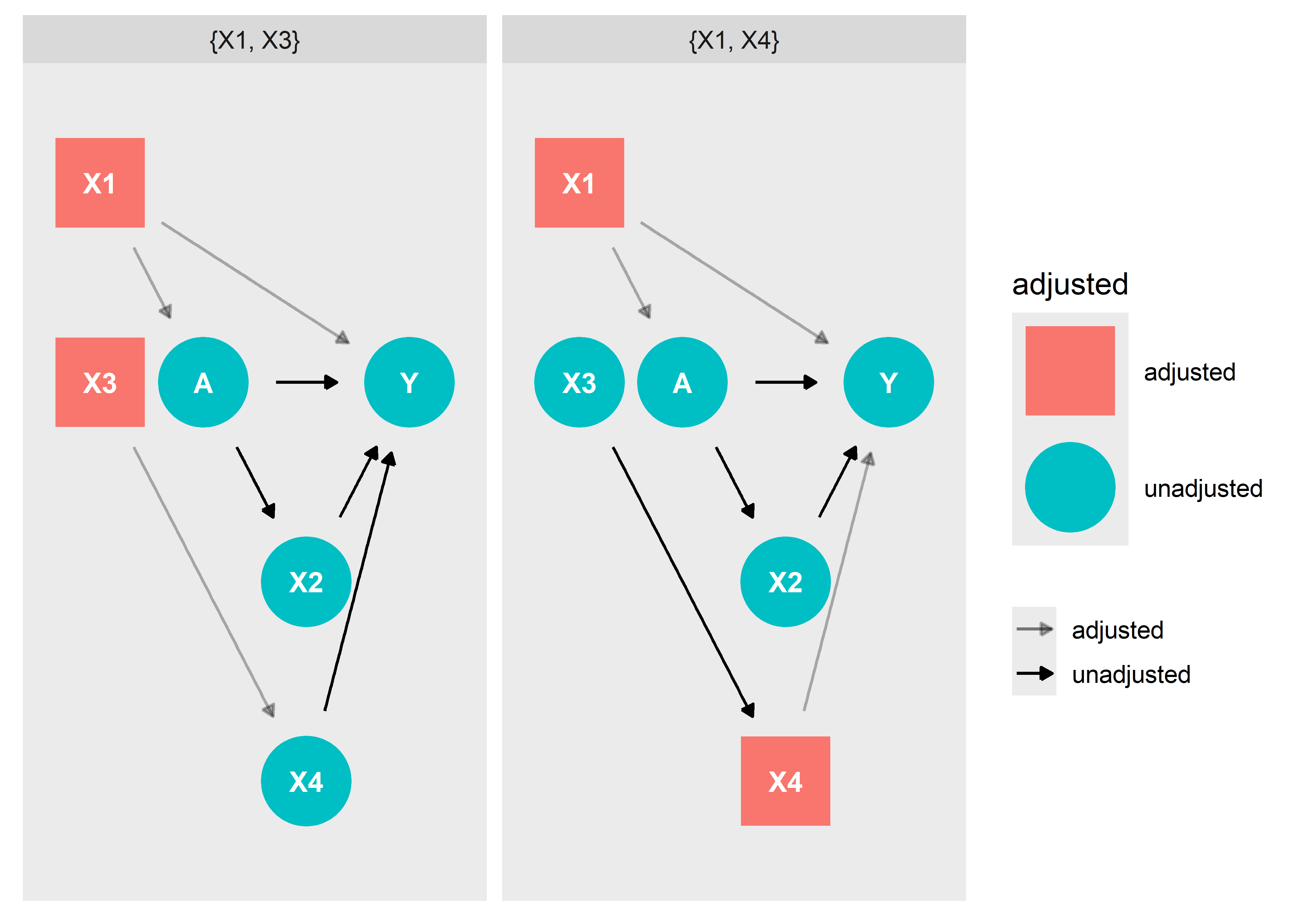

27.7.2 Independencias condicionales

Con el paquete dagitty podemos comprobar las implicaciones de nuestro DAG con la función impliedConditionalIndependencies.

Para nuestro DAG más simple (dag1) solo tenemos 1 independencia condicional:

impliedConditionalIndependencies(dag1)

X1 _||_ X2 | A

Esto quiere decir” “\(X_1\) es independiente de \(X_2\) dado \(A\)” o “\(X_1\) es independiente de \(X_2\) para cada nivel de \(A\)”.

En el caso de DAGs más complejos (dag2), la cantidad de independencias condicionales que se deben revisar son mayores:

impliedConditionalIndependencies(dag2)

A _||_ X4 | X3
X1 _||_ X2 | A
X1 _||_ X3
X1 _||_ X4
X2 _||_ X3 | A
X2 _||_ X4 | X3
X2 _||_ X4 | A
X3 _||_ Y | A, X1, X4

27.8 Modelo de regresión del desenlace

27.8.1 Caso de estudio

Usaremos ahora un ejemplo de la evaluación del uso de mosquiteros en disminuir el riesgo individual de infectarse de malaria (Andrew Heiss).

Las relaciones causales hipotetizadas por los investigadores estan propuestas en el siguiente DAG:

mosquito_dag <- dagify(
  malaria_risk ~ net + income + health + temperature + resistance,
  net ~ income + health + temperature + household,
  health ~ income + temperature,
  income ~ temperature + household,
  exposure = "net",
  outcome = "malaria_risk")

mosquito_dag %>%
  ggdag_status()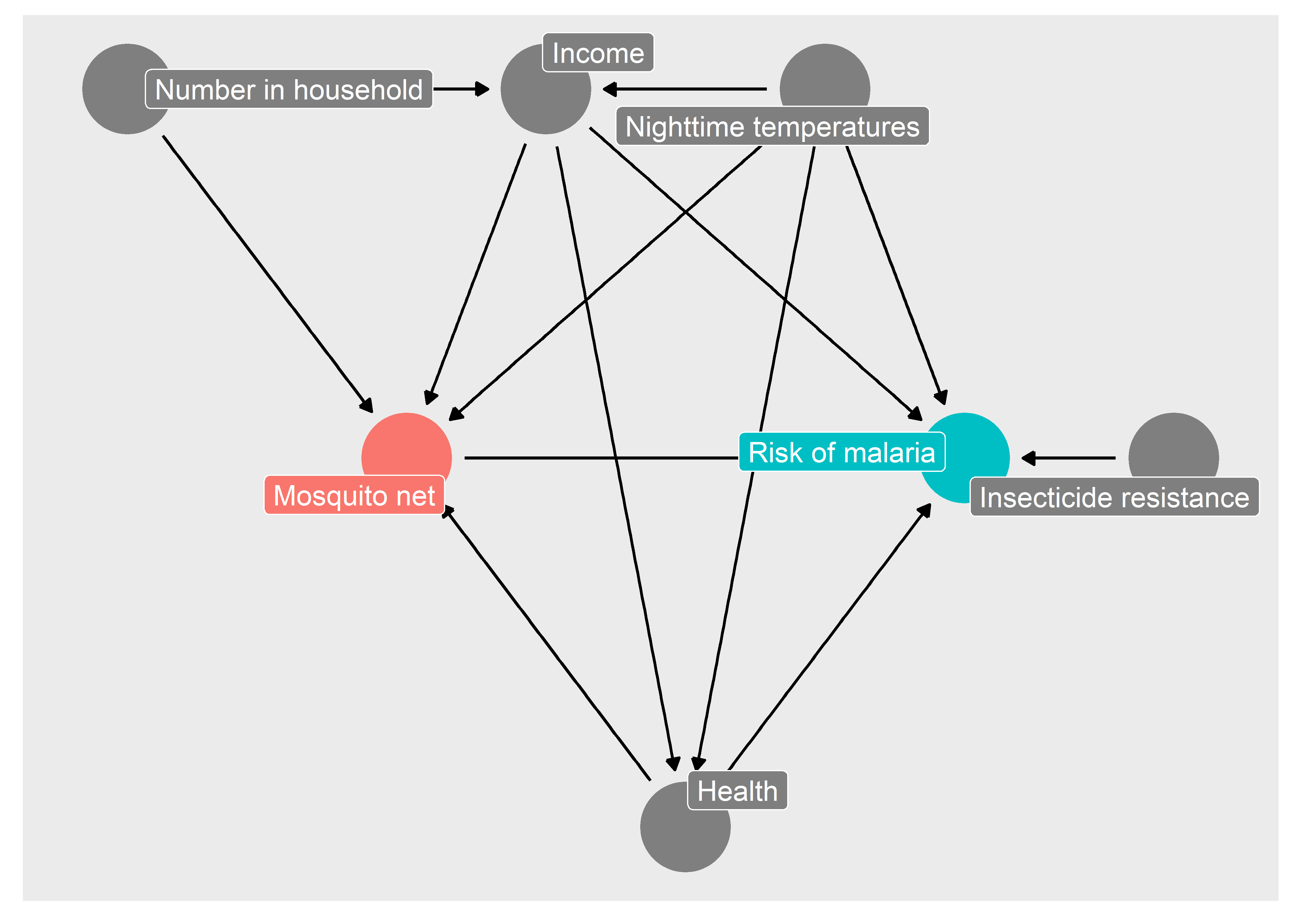

Cada uno de los nodos en el grafo es una columna en la base de datos que incluye las siguientes variables:

Riesgo de malaria (malaria_risk): La probabilidad de que alguien en el hogar se infecte con malaria. Medido en una escala de 0 a 100, donde los valores más altos indican un mayor riesgo.
Mosquitero (net y net_num): Variable binaria que indica si el hogar utilizaba mosquiteros y la cantidad de mosquiteros en la vivienda.
Ingreso (income): Ingreso mensual del hogar, en dólares estadounidenses.
Temperaturas nocturnas (temperature): La temperatura promedio durante la noche, en grados Celsius.
Salud (health): Salud autoinformada en el hogar. Medido en una escala de 0 a 100, donde los valores más altos indican una mejor salud.
Personas en el hogar (household): Número de personas que viven en el hogar.
Resistencia a los insecticidas (resistance): Algunas cepas de mosquitos son más resistentes a los insecticidas y, por lo tanto, presentan un mayor riesgo de infectar a las personas con malaria. Esto se mide en una escala de 0 a 100, donde los valores más altos indican una mayor resistencia.

27.8.2 Evaluación de supuestos

Usaremos la base de datos mosquito_nets.csv y la importaremos en R para hacer la evaluación de los supuestos y el modelos de regresión.

mosquito_nets <- read_csv("data/mosquito_nets.csv")

Las independendicas condicionales que se asumen para determinar el efecto causal entre el uso de mosquiteros y la reducción del riesgo de malaria son:

impliedConditionalIndependencies(mosquito_dag)

hlth _||_ hshl | incm, tmpr
hlth _||_ rsst
hshl _||_ mlr_ | hlth, incm, net, tmpr
hshl _||_ rsst
hshl _||_ tmpr
incm _||_ rsst
net _||_ rsst
rsst _||_ tmpr

Estas independencias condicionales podemos probarla frente a los datos que tenemos usando el comando localTests del paquete dagitty.

localTests(mosquito_dag, mosquito_nets)

	estimate	p.value	2.5%	97.5%
hlth \|\| hshl \| incm, tmpr	-0.0087701	0.7139357	-0.0556053	0.0381035
hlth \|\| rsst	0.0078410	0.7429670	-0.0390045	0.0546522
hshl \|\| mlr_ \| hlth, incm, net, tmpr	-0.0041409	0.8626678	-0.0510158	0.0427522
hshl \|\| rsst	0.0203648	0.3943280	-0.0264917	0.0671321
hshl \|\| tmpr	-0.0235562	0.3244643	-0.0703099	0.0233008
incm \|\| rsst	0.0137130	0.5662881	-0.0331395	0.0605054
net \|\| rsst	0.0167720	0.4829978	-0.0300828	0.0635534
rsst \|\| tmpr	-0.0219852	0.3577850	-0.0687458	0.0248716

En base a estos resultados podemos concluir que tenemos evidencia suficiente para satisfacer todas las independencia condicionales del DAG para identificar la relación causal entre el uso de mosquiteros y el riesgo de malaria.

27.8.3 Estimación del efecto causal

Ahora, determinamos el SMA para determinar el efecto causal total entre el uso de mosquiteros y el riesgo de malaria.

ggdag_adjustment_set(mosquito_dag, shadow = T, effect = "total")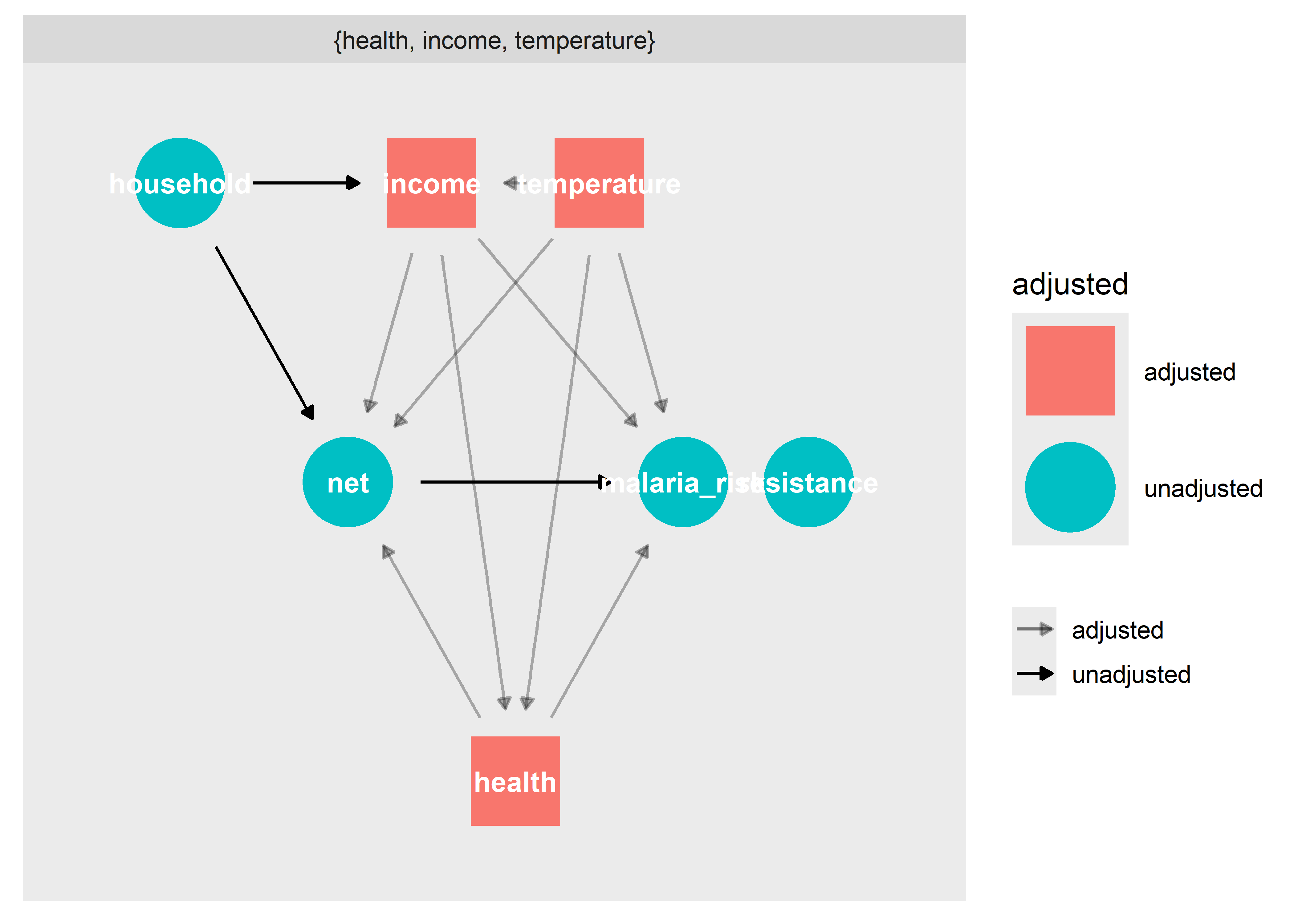

El SMA para determinar el efecto causal es: salud autoinformada (health), ingreso (income) y temperatura (temperature), los cuales consideraremos en nuestro modelo de regresión del desenlace.

library(jtools)

model_orm <- lm(malaria_risk ~ net + 
                 health + income + temperature,
               data = mosquito_nets)

summ(model_orm)

Observations	1752
Dependent variable	malaria_risk
Type	OLS linear regression

F(4,1747)	3366.41
R²	0.89
Adj. R²	0.88

	Est.	S.E.	t val.	p
(Intercept)	76.16	0.93	82.17	0.00
netTRUE	-10.44	0.26	-39.42	0.00
health	0.15	0.01	13.91	0.00
income	-0.08	0.00	-72.58	0.00
temperature	1.01	0.03	32.50	0.00
Standard errors: OLS

En base a los coeficientes de nuestro modelo, concluimos que el efecto causal total del uso de mosquiteros en el riesgo de malaria es de una disminución de la probabilidad de que alguien en el hogar se infecte con malaria en -10.44.

Nota

Es importante mencionar que el único coeficiente que es necesario reportar es el que corresponde al uso de mosquiteros (net) = -10.44. Los otros coeficientes en el modelo corresponden a las covariables del SMA y que no deberían reportarse para evitar errores en al interpretación como la falacia de la tabla 2.

27.9 Puntajes de propensión

Un enfoque alternativo para lidiar con los modelos estructurales es calcular para cada observación la probabilidad de asignación del tratamiento en base a la distribución de las covariables que satisfacen el cierre de todos los backdoor paths, esto se conoce como puntaje de propensión.

En casos tengamos SMA con muchas covariables, los enfoques tradicionales pueden resultar en un “problema de dimensionalidad”. Los puntajes de propensión resuelven este problema comprimiendo los factores relevantes en una única puntuación.

Luego, los individuos con puntajes de propensión similares pueden compararse entre los grupos expuestos y no expuestos.

Los puntajes de propensión fueron descritos por primera vez por Rosenbaum y Rubin en 1983 como una medida de la probabilidad de que un individuo reciba un tratamiento particular dado un conjunto de covariables medidas. Estos puntajes de propensión se pueden usar en 3 tipos de estrategias:

Estratificación
Emparejamiento
Ponderación (IPTW)

27.9.1 Creación de PS

Existen muchas maneras para determinar la probabilidad de la asignación del tratamiento en base a la distribución de las covariables, desde métodos tradicionales como regresiones logísticas o probit hasta métodos más flexibles como machine learning.

Lo importante es seguir la estrategia de identificación y solo incluir las variables que cierran todas los backdoor paths identificados en nuestro DAG.

En nuestro caso, construiremos un modelo de regresión logística para predecir la probabilidad de tener o no un mosquitero en base a la salud autoinformada (health), ingreso (income) y temperatura (temperature).

ps_net <- glm(net ~ income + temperature + health,
                 data = mosquito_nets,
                 family = binomial(link = "logit"))

Luego podemos utilizar los valores de los ingresos, las temperaturas y la salud autoinformada de cada observación de nuestra base de datos y generar una predicción de la probabilidad utilizando este modelo.

mosquito_nets <- mosquito_nets %>%
  mutate(ps = predict(ps_net, 
                      type = "response"))

Inspeccionamos la distribución de nuestros puntajes de propensión para cada grupo de la exposición.

mosquito_nets %>%
  ggplot(aes(x = ps, fill = net)) +
  geom_histogram(aes(y = ..count..), 
                 data = ~filter(., net == T)) +
  geom_histogram(aes(y = -..count..),
                 data = ~filter(., net != T)) +
  geom_hline(yintercept = 0) +
  theme_bw()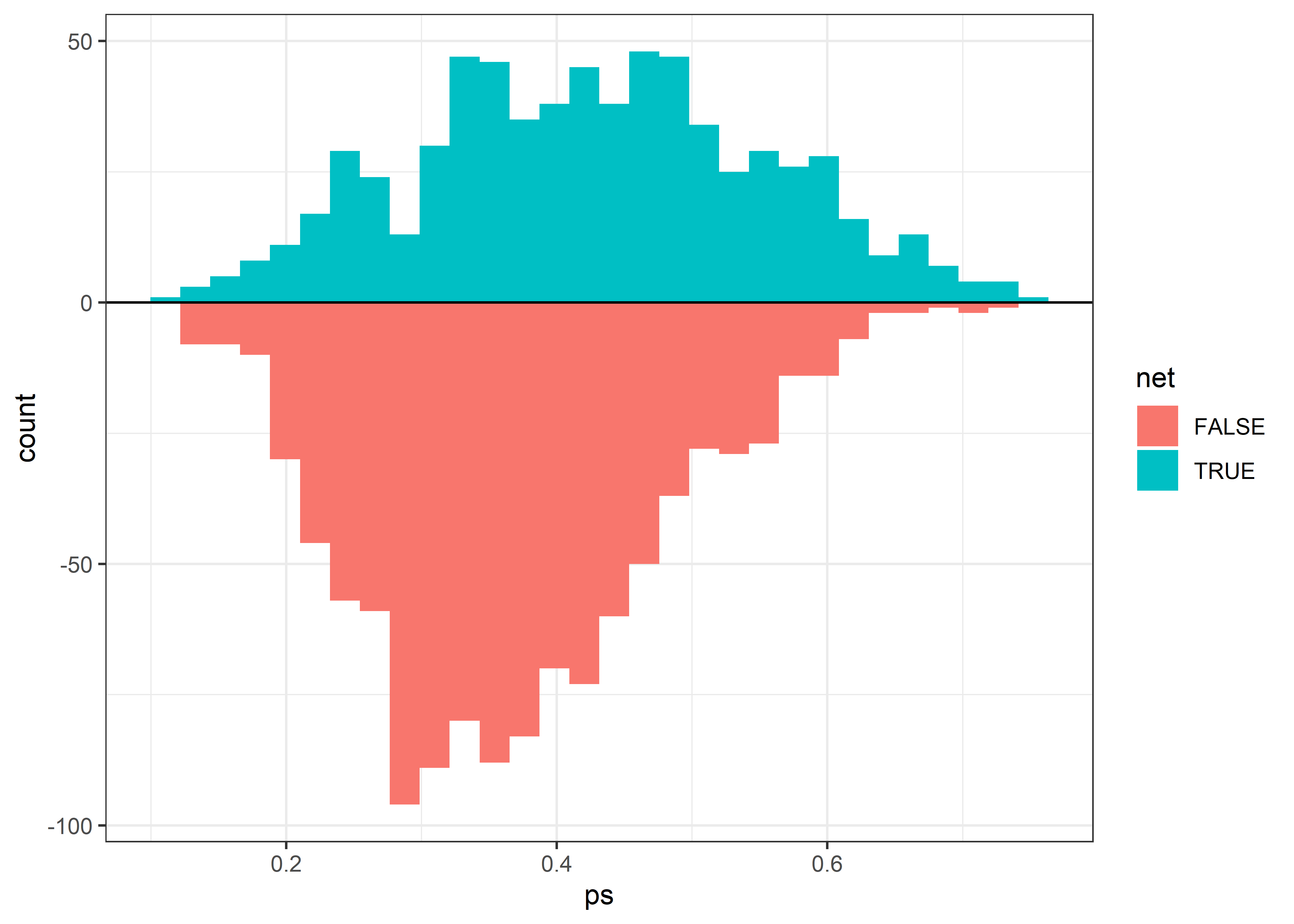

Nota

Es importante recordar que los puntajes de propensión solo balancean las covariables medidas, lo que no evita la confusión residual causada por factores no medidos (no puede controlar variables no medidas o medidas imperfectamente). Por lo tanto, no se puede excluir completamente el error sistemático residual (factor de confusión).

27.9.2 Estratificación de PS

Con los PS que hemos creado podemos estratificarlos en percentiles (por ejemplo quintiles) y estratificar nuestro modelo de regresión.

mosquito_nets <- mosquito_nets %>%
  mutate(q_ps = cut_number(ps,5))

library(lme4)
model_ps_str <- lmer(malaria_risk ~ net + (net | q_ps),
                     data = mosquito_nets)

summ(model_ps_str)

Observations	1752
Dependent variable	malaria_risk
Type	Mixed effects linear regression

AIC	11635.45
BIC	11668.26
Pseudo-R² (fixed effects)	0.13
Pseudo-R² (total)	0.83

Fixed Effects
	Est.	S.E.	t val.	d.f.	p
(Intercept)	39.72	6.44	6.17	4.00	0.00
netTRUE	-11.65	1.79	-6.52	4.00	0.00
p values calculated using Satterthwaite d.f.

Random Effects
Group	Parameter	Std. Dev.
q_ps	(Intercept)	14.40
q_ps	netTRUE	3.93
Residual		6.60

Grouping Variables
Group	# groups	ICC
q_ps	5	0.83

Sin embargo, es posible que esta estrategia agregue sesgo debido al desbalance residual dentro de los estratos.

27.10 Emparejamiento de PS

Otra estrategia para eliminar todos los backdoor paths es el emparejamiento (Matching en inglés). Con este método, para cada observación que ha recibido el tratamiento o exposición le buscamos una pareja que tenga caracteristicas iguales o semejantes para que sean comparables. Usaremos el paquete MatchIt para realizar la busqueda de las parejas.

Existe una gran variedad de ténicas para hacer el emparejamiento. En este caso usaremos la estrategia del vecino más cercano (nearest) y con una distancia de Mahalanobis, pero se puede explorar el repertorio de metodos en la documentación del paquete.

27.10.1 Creación de las parejas

Buscaremos observaciones con valores similares de ingresos, temperatura y salud autoinformada que usaron y no usaron mosquiteros. El argumento replace = TRUE permite las observaciones que ya se han emparejado puedan volverse a emparejar.

library(MatchIt)

set.seed(2023)

matched_data <- matchit(net ~ income + temperature + health,
                        data = mosquito_nets,
                        method = "nearest",
                        distance = "mahalanobis",
                        replace = TRUE)
summary(matched_data)


Call:
matchit(formula = net ~ income + temperature + health, data = mosquito_nets, 
    method = "nearest", distance = "mahalanobis", replace = TRUE)

Summary of Balance for All Data:
            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
income           955.1938      872.7526          0.4089     1.3633    0.1044
temperature       23.3809       24.0880         -0.1685     1.0846    0.0424
health            54.9090       48.0570          0.3619     1.2083    0.0714
            eCDF Max
income        0.1983
temperature   0.0972
health        0.1683

Summary of Balance for Matched Data:
            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
income           955.1938      950.1836          0.0248     1.1061    0.0093
temperature       23.3809       23.4066         -0.0061     1.0335    0.0067
health            54.9090       54.5433          0.0193     1.0714    0.0073
            eCDF Max Std. Pair Dist.
income        0.0485          0.1202
temperature   0.0264          0.1196
health        0.0264          0.1239

Sample Sizes:
              Control Treated
All           1071.       681
Matched (ESS)  320.94     681
Matched        436.       681
Unmatched      635.         0
Discarded        0.         0

Los 681 usuarios de mosquiteros (Treated) se emparejaron con no usuarios de mosquiteros (Control) de apariencia similar (436 de ellos). 635 personas no fueron emparejadas y serán descartadas.

Para revisar el balance de las covariables podemos comparar la diferencia promedio estandarizada antes y después del emparejamiento. Una forma visual y sencilla de revisar esto es un love.plot del paquete cobalt.

library(cobalt)

love.plot(matched_data, var.order = "unadjusted", stats = "mean.diffs")

En este caso observamos un buen balance de las covariables después de hacer el emparejamiento (puntos azules cercanos a 0).

A continuación, crearemos un nuevo dataset con las parejas usando la función match.data().

dat_m <- match.data(matched_data)

27.10.2 Estimación del efecto causal

Con este nuevo set de datos, estimamos el efecto de mosquiteros en el riesgo de malaria. Los confusores identificados en el DAG han sido tomados en cuenta en la estrategia de emparejamiento, por lo que solo necesitamos correr una regresión simple.

model_ps_match <- lm(malaria_risk ~ net,
              data = dat_m)

summ(model_ps_match)

Observations	1117
Dependent variable	malaria_risk
Type	OLS linear regression

F(1,1115)	274.97
R²	0.20
Adj. R²	0.20

	Est.	S.E.	t val.	p
(Intercept)	38.33	0.60	63.95	0.00
netTRUE	-12.73	0.77	-16.58	0.00
Standard errors: OLS

27.10.3 Desbalance de parejas

Al usar el argumento replace = TRUE en nuestro emparejamiento es posible que algunas observaciones esten sobre-representadas y tengan una mayor importancia en el modelo. matchit() proporciona una columna con los pesos (weights) que permite considerar esta sobre-representación de observaciones.

model_ps_match_w <- lm(malaria_risk ~ net,
              data = dat_m,
              weights = weights)

summ(model_ps_match_w)

Observations	1117
Dependent variable	malaria_risk
Type	OLS linear regression

F(1,1115)	188.00
R²	0.14
Adj. R²	0.14

	Est.	S.E.	t val.	p
(Intercept)	36.09	0.60	60.45	0.00
netTRUE	-10.48	0.76	-13.71	0.00
Standard errors: OLS

27.11 Ponderación de probabilidad inversa al tratamiento (IPTW)

Una limitación importante del emparejamiento (matching) es que generalmente se excluye una cantidad importante de observaciones que no ha podido ser emparejada.

A pesar de reducir los problemas de dimensionalidad, los PS en estrategias de estratificación y emparejamiento utilizan los datos de la muestra, por lo que siguen existiendo combinaciones de covariables que son poco representadas en la población de análisis (muestra).

Una tecnica para afontar este problema es la Ponderación de probabilidad inversa al tratamiento (IPTW). Esta técnica pertenece a un grupo más amplio de estrategias que se conoce como G-methods (o métodos de generalización).

Estos métodos permiten:

Simular el efecto causal marginal en la población.
Crear una pseudo-población.
“Eliminar” los enlaces (relaciones) entre nodos en el DAG.

IPTW crea una pseudo-población en la que se elimina los enlaces (relaciones) entre nodos, principalmente, desde los factores de confusión \(L\) hasta el tratamiento \(A\).

Por lo tanto, si los factores de confusión \(L\) son suficientes (supuesto de intercambiabilidad condicional) para bloquear todas las rutas de puerta trasera (backdoor paths) desde el tratamiento \(A\) hasta el desenlace \(Y\), entonces todos los factores de confusión se eliminan en la pseudo-población. Es decir, la asociación entre \(A \rightarrow Y\) en la pseudo-población estima, consistentemente, el efecto causal de \(A\) sobre \(Y\).

Al calcular el puntaje de propensión hemos estimado la probabilidad la asignación del tratamiento \(A\) en base a la distribución de los confusores \(L\). Sin embargo, para poder determinar el efecto causal, desearíamos que la distribución de estas variables (confusoras) este balanceada entre los grupos que recibieron y no recibieron el trabamiento \(A\).

Si una característica (de una variable confusora) ha sido poco frecuente en el grupo expuesto y muy frecuente en el grupo no expuesto revertiremos ese desbalance usando la ponderación inversa (cuanto menos frecuente sea la observación —y sus covariables— en la muestra, mayor será la población que debería representar).

Las características poco frecuentes en alguno de los grupos de tratamiento tendrán un mayor peso y las características muy frecuentes tendrán un menor peso.

Estos pesos diferenciados crearan una distribución balanceada en una pseudo-población no observable. Nuestra muestra original sigue teniendo la distribución de covariables desbalanceada original. En consecuencia, solo será posible estimar el efecto causal en una pseudo-población donde se ha logrado el balance de las variables confusoras con respecto a la asignación del tratamiento.

27.11.1 Creación de los pesos

Una vez tengamos los puntajes de propensión (PS), calculamos los pesos (\(W^A\)) como \(\frac{1}{PS}\) para los que recibieron la exposición/tratamiento y \(\frac{1}{1-PS}\) para los que los que no recibieron la exposición/tratamiento.

Alternativamente se puede usar esta formula (Ecuación 27.1) para definir los pesos si la variable de exposición/ tratamiento esta codificada como 0/1.

\[ {IPT} = \frac{Tratamiento}{Propensión} + \frac{1-Tratamiento}{1-Propensión} \tag{27.1}\]

mosquito_nets <- mosquito_nets %>%
  mutate(ipt = ifelse(net==T, 1/ps, 1/(1-ps)),
         ipt2 = (net/ps) + ((1-net) / (1-ps)))

Ahora revisaremos la distribución de los pesos que usaremos:

mosquito_nets %>%
  ggplot(aes(ipt)) +
  geom_histogram() +
  theme_bw()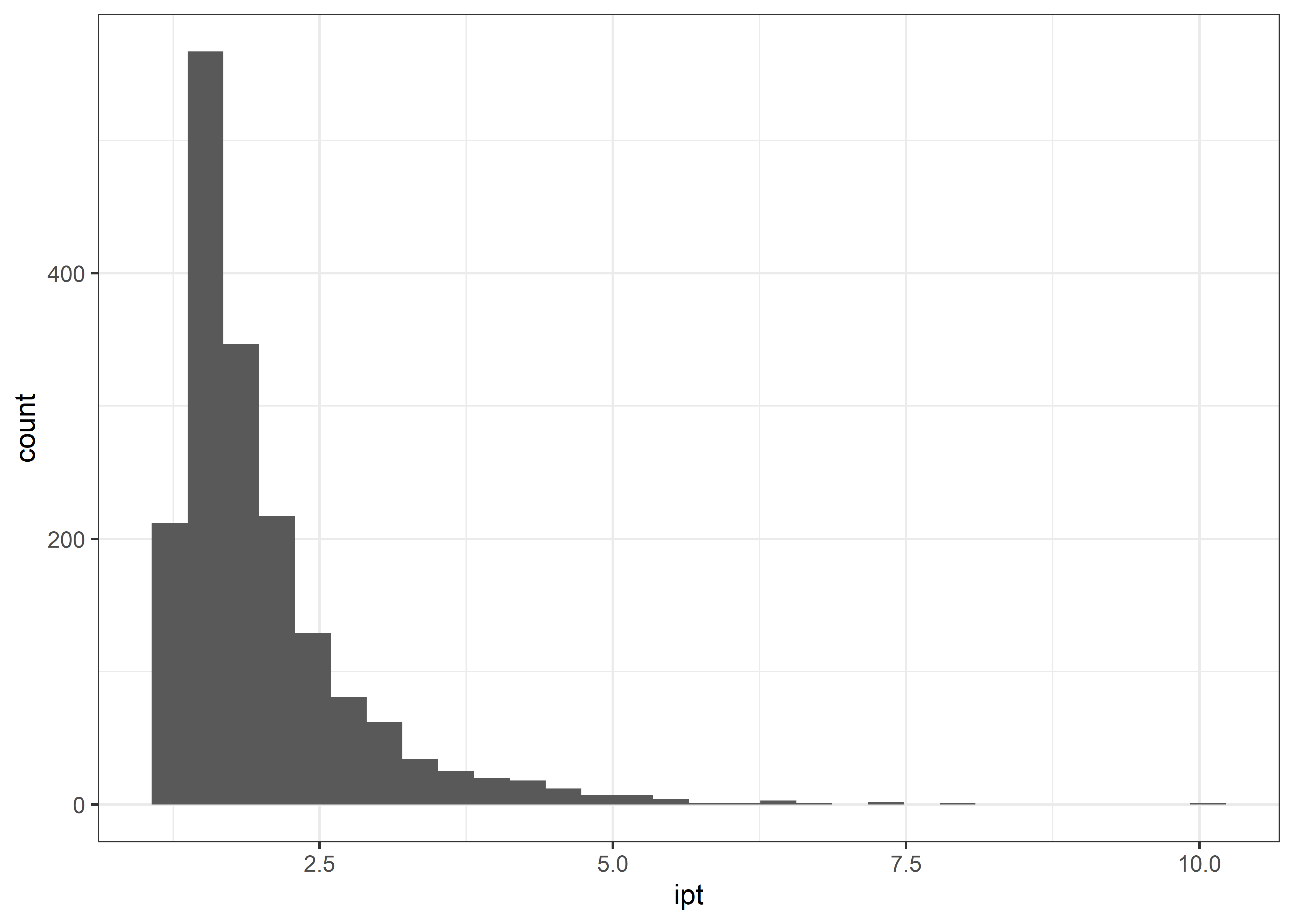

El rango de nuestros pesos va de 1.14 a 9.99 y tiene una distribución muy sesgada a la derecha. Es decir, existen algunos pocos participantes que en base a la distribución de sus covariables (confusoras) lo más probable era que no reciba el tratamiento (net), sin embargo, lo recibió.

id	net	malaria_risk	income	health	temperature	resistance	ps	ipt
877	TRUE	81	336	20	29.2	46	0.1000789	9.992114

Lo exploraremos de forma visual:

El individuo 877 es el único punto amarillo en nuestro gráfico. Tiene el mayor peso por que la distribución de sus covariables (income, health, temperature) es muy poco frecuente dentro del grupo que recibió mosquiteros (tratamiento).

No hay una regla definida en el valor máximo de un peso para el uso de IPTW, sin embargo la estimación de IPTW puede ser inestable cuando algunos valores del tratamiento \(A\) no son frecuentes, entonces el denominador del peso (\(Pr(A|L)\)) puede ser muy pequeño.

Una solución es utilizar un factor estabilizador (\(SW^A\)); esto reduce la varianza de las ponderaciones y da como resultado estimaciones del efecto más precisas usando \(Pr(A=1)\) en el numerador de los que recibieron el tratamiento y \(Pr(A=0)\) en el numerador de los que no recibieron el tratamiento.

ps_net_s <- glm(net ~ 1,
                 data = mosquito_nets,
                 family = binomial(link = "logit"))

mosquito_nets <- mosquito_nets %>%
  mutate(p = predict(ps_net_s, 
                     type = "response"),
         ipt_s = ifelse(net==T, 
                        p/ps, 
                        (1-p)/(1-ps)))

Y observamos que ahora tiene una distribución con un rango más acotado.

mosquito_nets %>%
  ggplot(aes(ipt_s)) +
  geom_histogram() +
  theme_bw()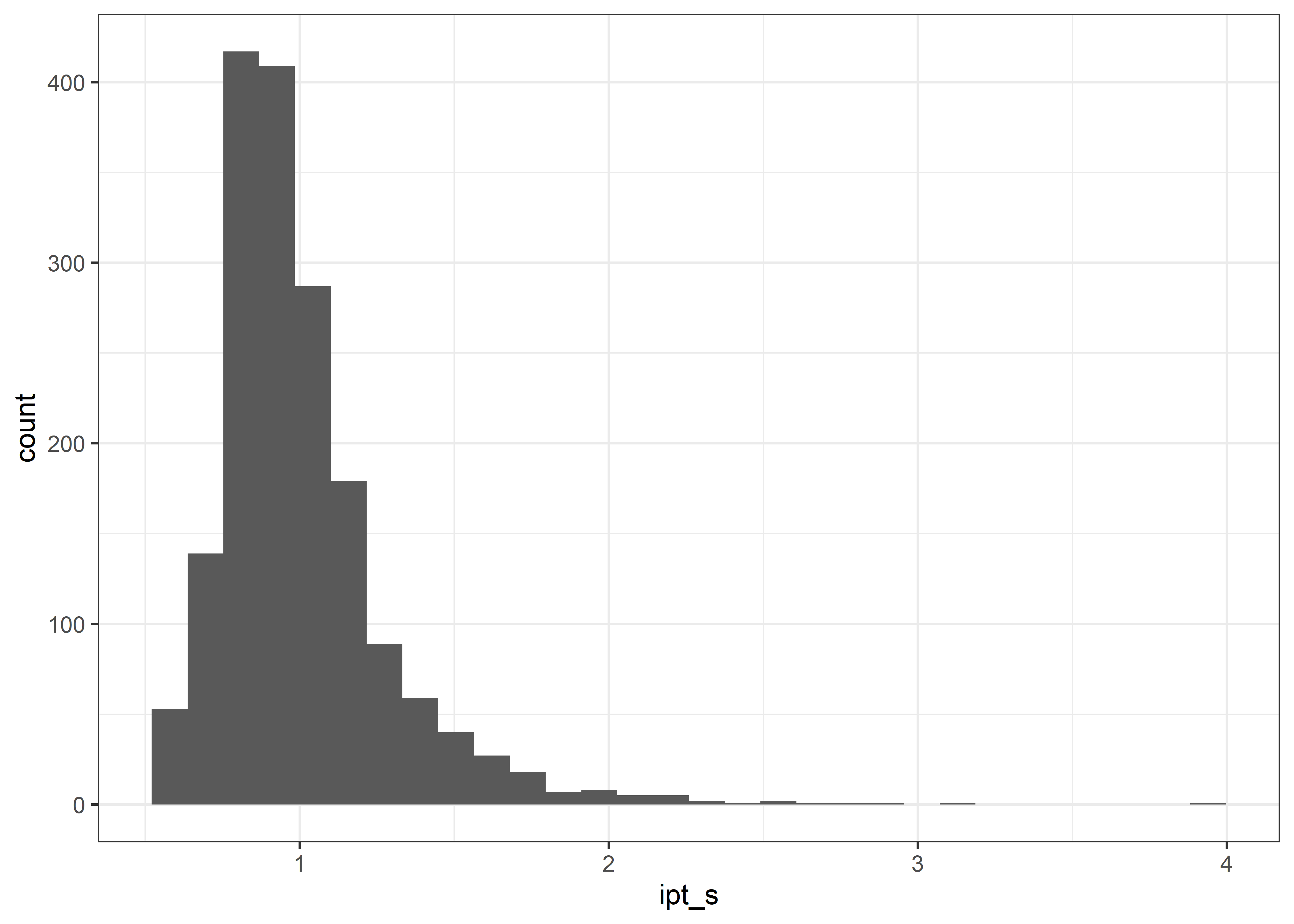

Nota

Un paquete recomendado para el cálculo de los pesos usando una variedad importante de métodos para diferentes estimaciones (ATE, ATT, ATC, ATO, ATM, etc.) es WeightIt.

27.11.2 Modelos estructurales marginales (MSM)

Los modelos estructurales marginales (MSM) son una nueva clase de modelos causales para la estimación, a partir de datos observacionales, del efecto causal de una exposición (dependiente del tiempo) en presencia de covariables (dependientes del tiempo) que pueden ser simultáneamente factores de confusión y variables intermedias (Robins, Hernán & Babette, 2000).

En nuestro caso, estamos viendo una versión más sencilla de la aplicación de los MSM, donde no existen variables dependientes del tiempo.

Si el objetivo de la pregunta de investigación no es analizar la modificación de efecto (en la escala aditiva o multiplicativa), entonces el MSM esta compuesto de la siguiente forma:

\[ {E[Y^a]} = \beta_0 + \beta_1a \tag{27.2}\]

La variable dependiente en este modelo es un desenlace potencial (es decir, no observable).

Ajustaremos el modelo anterio (Ecuación 27.2) usando IPTW (regresión ponderada por \(W^A\) o \(SW^A\) basado en un conjunto suficiente de factores de confusión para lograr la intercambiabilidad).

model_iptw <- lm(malaria_risk ~ net,
                 data = mosquito_nets,
                 weights = ipt_s)

summ(model_iptw)

Observations	1752
Dependent variable	malaria_risk
Type	OLS linear regression

F(1,1750)	222.45
R²	0.11
Adj. R²	0.11

	Est.	S.E.	t val.	p
(Intercept)	39.68	0.43	92.99	0.00
netTRUE	-10.13	0.68	-14.91	0.00
Standard errors: OLS

En base a los resultados del modelo, podemos concluir que el Efecto (causal) promedio del tratamiento (ATE) es de -10.13.

Nota

La definición de la mejor estrategia para identificar el efecto causal sigue siendo un campo abierto a debate y desarrollo como se muestra en el comentarios de Noah Greifer.