13 Regresión lineal: Evaluación y extensiones
En este capítulo se verán algunas herramientas en R para el chequeo de la adecuación, la evaluación del ajuste y la selección de modelos de regresión lineal. Además, se tratará brevemente sobre transformaciones sobre la variable predictora y la regresión polinomial.
Usaremos el conjunto de datos fev del Capítulo 12. Llamaremos también al paquete tidyverse:
13.1 Chequeo de la adecuación del modelo
Según el aforismo “todos los modelos son incorrectos, pero algunos son útiles”, ningún modelo que usemos podrá explicar de manera perfecta cómo es la asociación entre la variable de respuesta y los predictores. Sin embargo, los modelos son útiles porque sirven como un mecanismo para explorar y describir ciertas generalidades de la asociación, dado que el modelo sea adecuado.
Si partimos del hecho de que es seguro que nuestro modelo no exprese perfectamente la verdadera asociación entre la respuesta y los predictores, entonces lo que nos queda es verificar que no haya evidencias en contra del modelo. En particular, en un modelo de regresión lineal, los aspectos más importantes a evaluar son los siguientes:
- Los errores son independientes y tienen varianza constante (homocedasticidad),
- Los errores provienen de una distribución normal. Este supuesto es importante solo cuando se quiere hacer inferencias del modelo.
Generalmente, se usa los residuales que produce el modelo ajustado para evaluar estos supuestos, ya que estos pueden ser considerados como estimaciones de los errores. Sin embargo, no necesariamente tienen todas las propiedades de los errores. Por ejemplo, los residuales no son independientes. No obstante, esto no afecta mucho en la utilidad de estos para detectar evidentes violaciones de los supuestos de los errores.
Existe otro supuesto llamado de linealidad que generalmente es malinterepretado. Esta linealidad hace referencia a que en un modelo del tipo
13.1.0.1 Análisis de residuales
La mejor forma de diagnóstico de cualquier modelo es la visual. Podemos generar varios tipos de gráficos de residuales en R para evaluar diferentes aspectos del modelo. La función plot() genérica de R permite generar cuatro gráficos básicos para el análisis de residuales.
Usemos, por ejemplo, el modelo para el volumen espiratorio forzado con la altura y la edad como predictores:
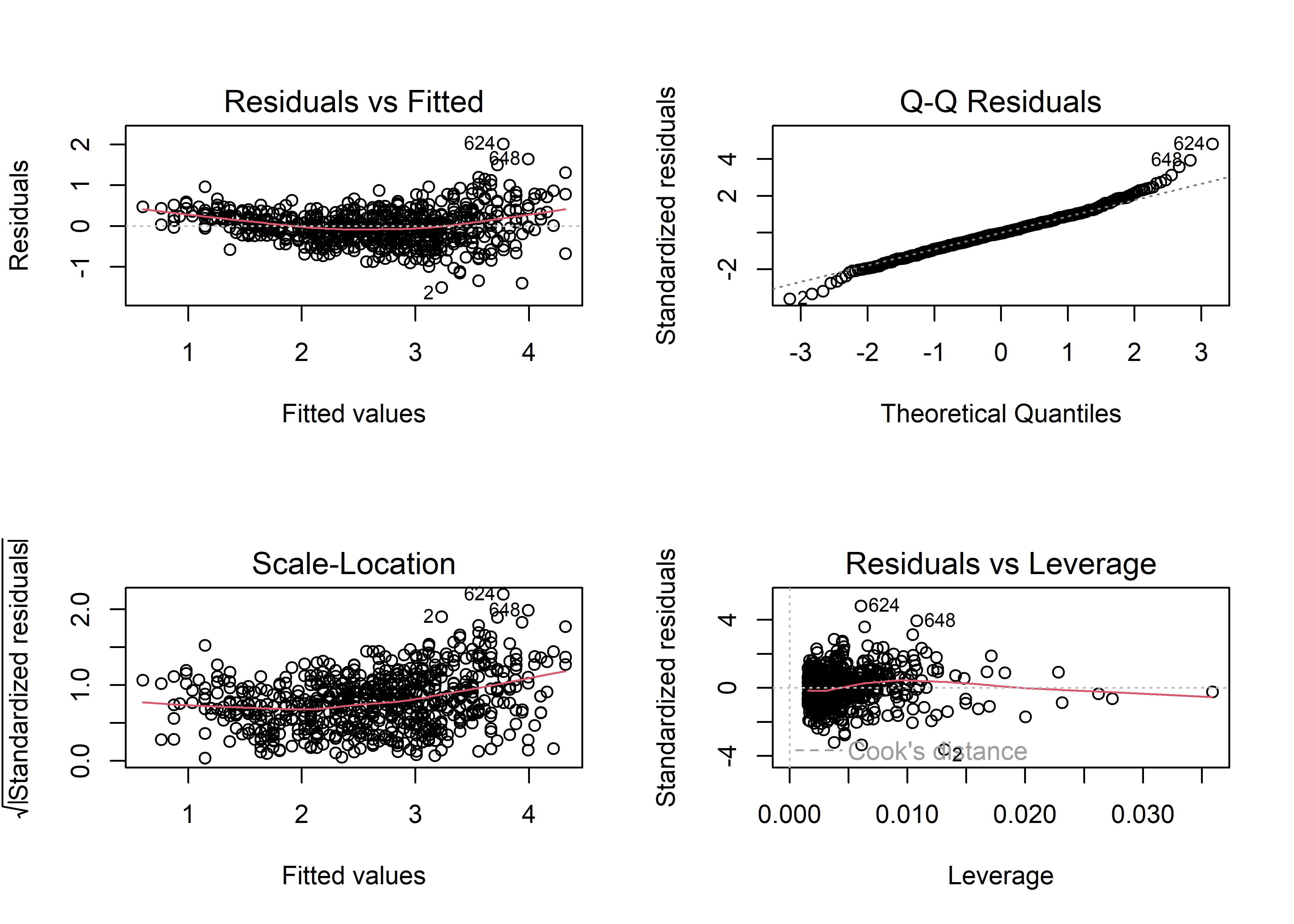
fit_multiple <- lm(fev ~ hgt + age, data = fev)La función plot() muestra los gráficos de manera independiente. Para verlos agrupados en una sola imagen, podemos decirle a R que los disponga en un arreglo de 2x2 (2 filas, 2 columnas). Para establacer parámetros gráficos en R base, podemos usar la función par(). El parámetro gráfico que controla la disposición de los gráficos es mfrow. Para decirle a R que queremos disponer los gráficos en un arreglo de 2x2, pasamos al parámetro mfro el vector c(2, 2), donde el primer elemento representa el número de filas y el segundo el número de columnas:
El gráfico de Residuals vs. Fitted nos sirve para evaluar la desviación general de las observaciones del modelo ajustado de regresión. La línea horizontal de referencia en el valor 0 representa la línea o recta de regresión. Las observaciones para las cuales su valor ajustado es muy diferente tendrán residuales de mayor magnitud, y por tanto aparecerán más distantes a la línea de referencia. Distinguimos en este gráfico un patrón ligeramente curvilíneo en los residuales. Esto podría indicar que la respuesta podría estar asociada a alguna transformación no-lineal de alguno de los predictores. Más adelante veremos que para evaluar si es necesario transformar alguno de los predictores podemos usar gráficos de residuales marginales. Además, vemos que la dispersión de los residuales es mayor para valores altos de los valores ajustados, lo cuál podría indicar un problema de heterocedasticidad o varianza no constante. El gráfico también nos muestra el número de fila de 3 observaciones con residuales más grandes en magnitud. En este caso, resalta las observaciones 2, 624 y 648. Estas observaciones son potencialmente outliers o observaciones influyentes, por lo que no hay que perderlas de vista.
El gráfico de Q-Q Residuals es útil para evaluar el supuesto de normalidad de los errores. Si los errores efectivamente provienen de una distribución normal, los residuales deberían mostrar una tendencia a alinearse con los cuantiles teóricos de la distribución normal en el eje X y seguir la línea de referencia. Vemos que, en general, este es el caso, excepto las colas de la distribución de residuales que parecen desviarse moderadamente de la línea de referencia. Esto es común cuando se trabaja con una muestra grande. Algo alarmante en este gráfico sería una desviación excesiva y sistemática de los residuales a lo largo de línea de referencia.
El gráfico de Scale-Location es similar al gráfico de Residuals vs. Fitted. Sin embargo, el primero es más apropiado ya que utiliza una transformación de los residuales estandarizados que disminuye el sesgo de la distribución. Vemos un patrón ligeramente curvilíneo y mayor dispersión presente a medida que aumenta el valor de los valores ajustados. Estos patrones son similares al del gráfico de Residuals vs. Fitted.
Por último, el gráfico de Residuals vs. Leverage nos sirve para identificar observaciones influyentes. La inclusión de este tipo de observaciones puede potencialmente alterar el resultado final del ajuste del modelo. Las observaciones con residuales y leverage altos son potencialmente observaciones influyentes. En este gráfico también se muestran contornos con la distancia de Cook. En este caso particular, los contornos no se observan ya que están fuera de los límites del gráfico Podemos ampliar los límites del gráfico especificando la fracción por la cual se va a extender los límites usando el parámetro extend.ylim.f de la función plot(). Además, también tenemos que seleccionar el gráfico de Residuals vs. Leverage con el parámetro which. Según la documentación (ver help(plot.lm), este gráfico es el número 5. Usemos extend.ylim.f = 1 para visualizar mejor los contornos:
plot(fit_multiple, which = 5, extend.ylim.f = 1)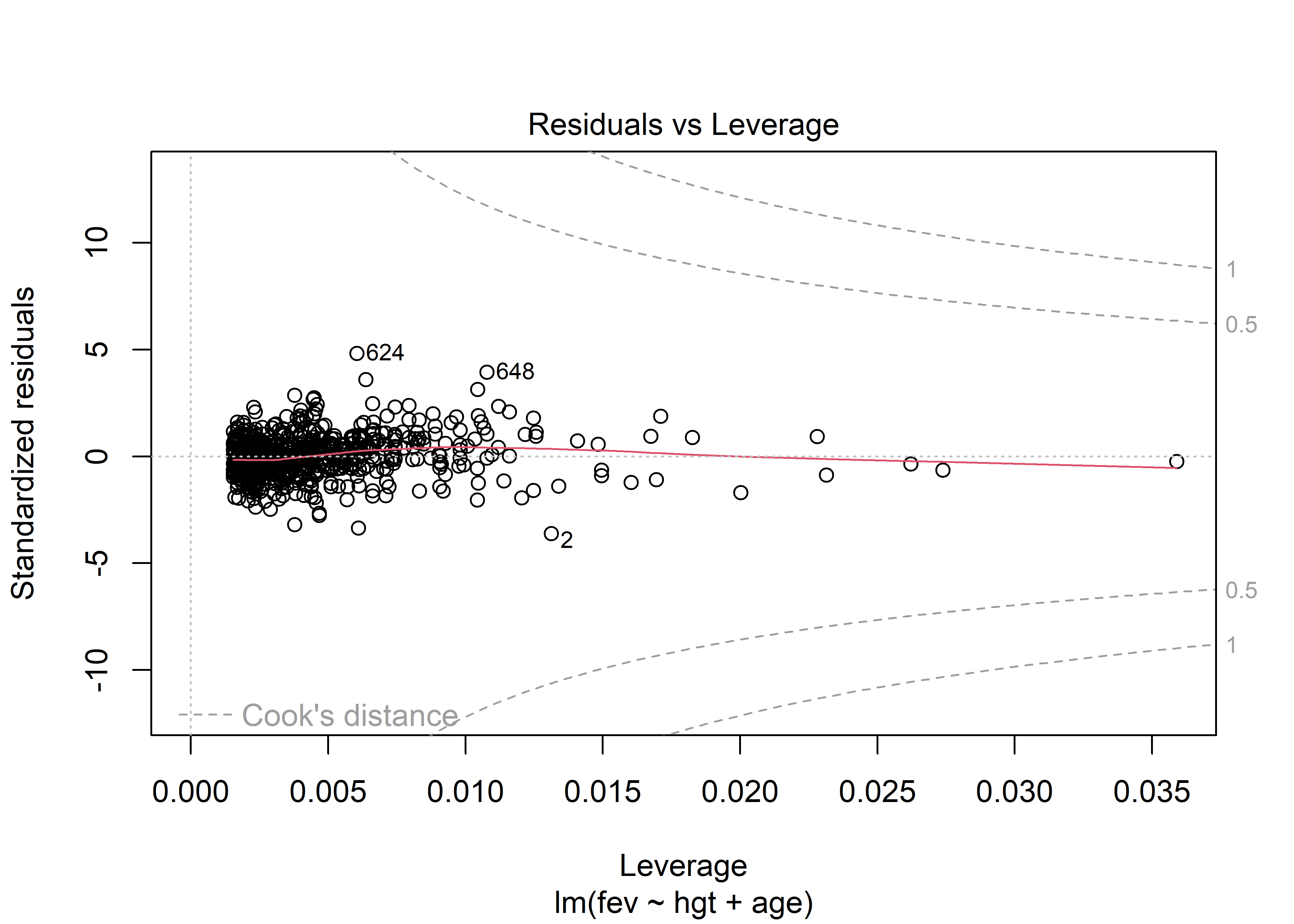
Aquellas observaciones que sobrepasen estos contornos requieren revisión, ya que son muy probablemente observaciones influyentes. En este caso, ninguna observación está próxima ni sobrepasa los contornos. Lo que sí vemos son observaciones con alto leverage, lo cual indicaría la presencia de outliers con respecto a la variable de respuesta.
Para generar gráficos para el análisis de residuales al estilo de ggplot2, podemos usar la función autplot(). Es necesario llamar antes al paquete ggfortify.
autoplot(fit_multiple)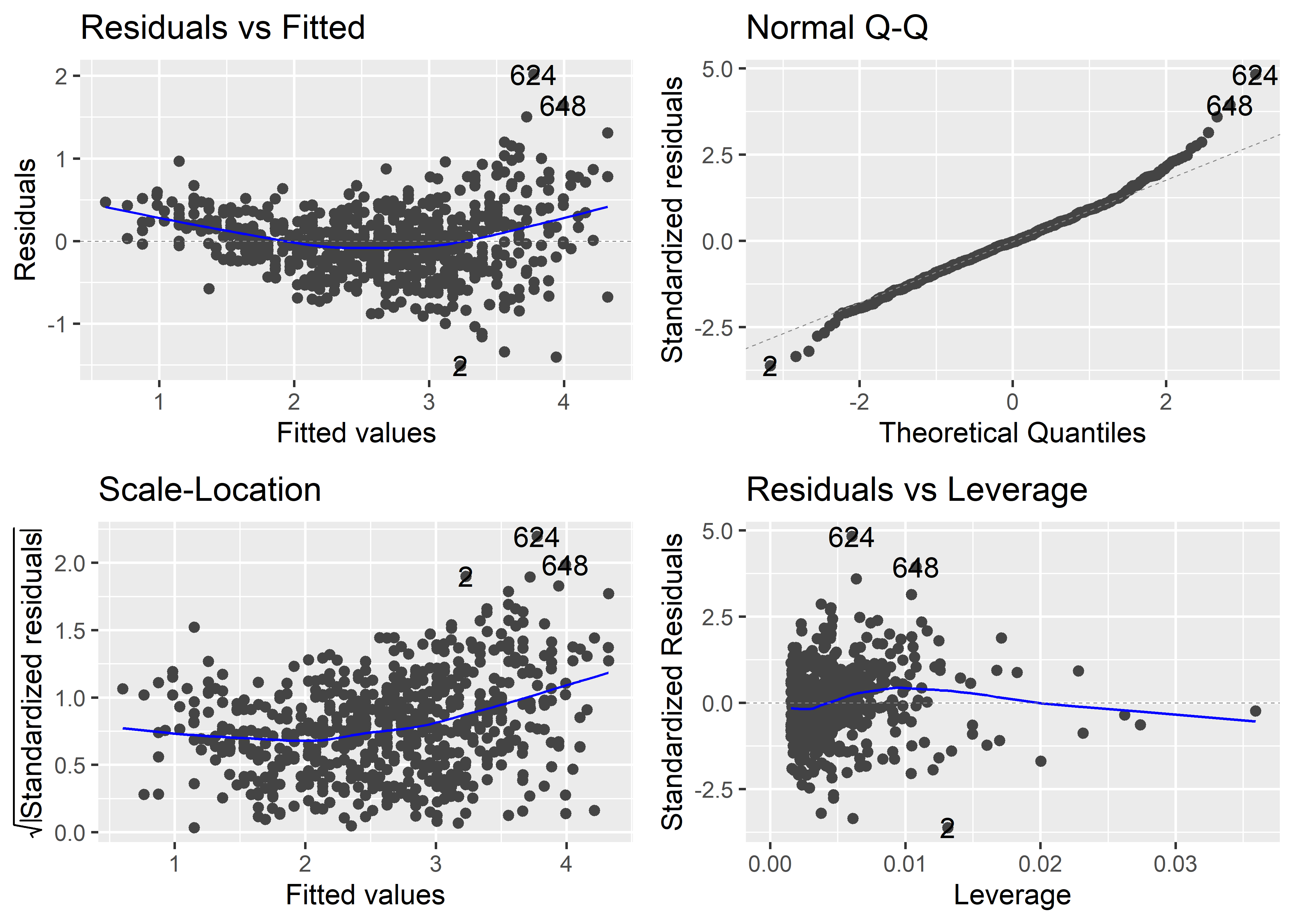
Otra función bastante útil es la función check_model() del paquete performance:
check_model(fit_multiple)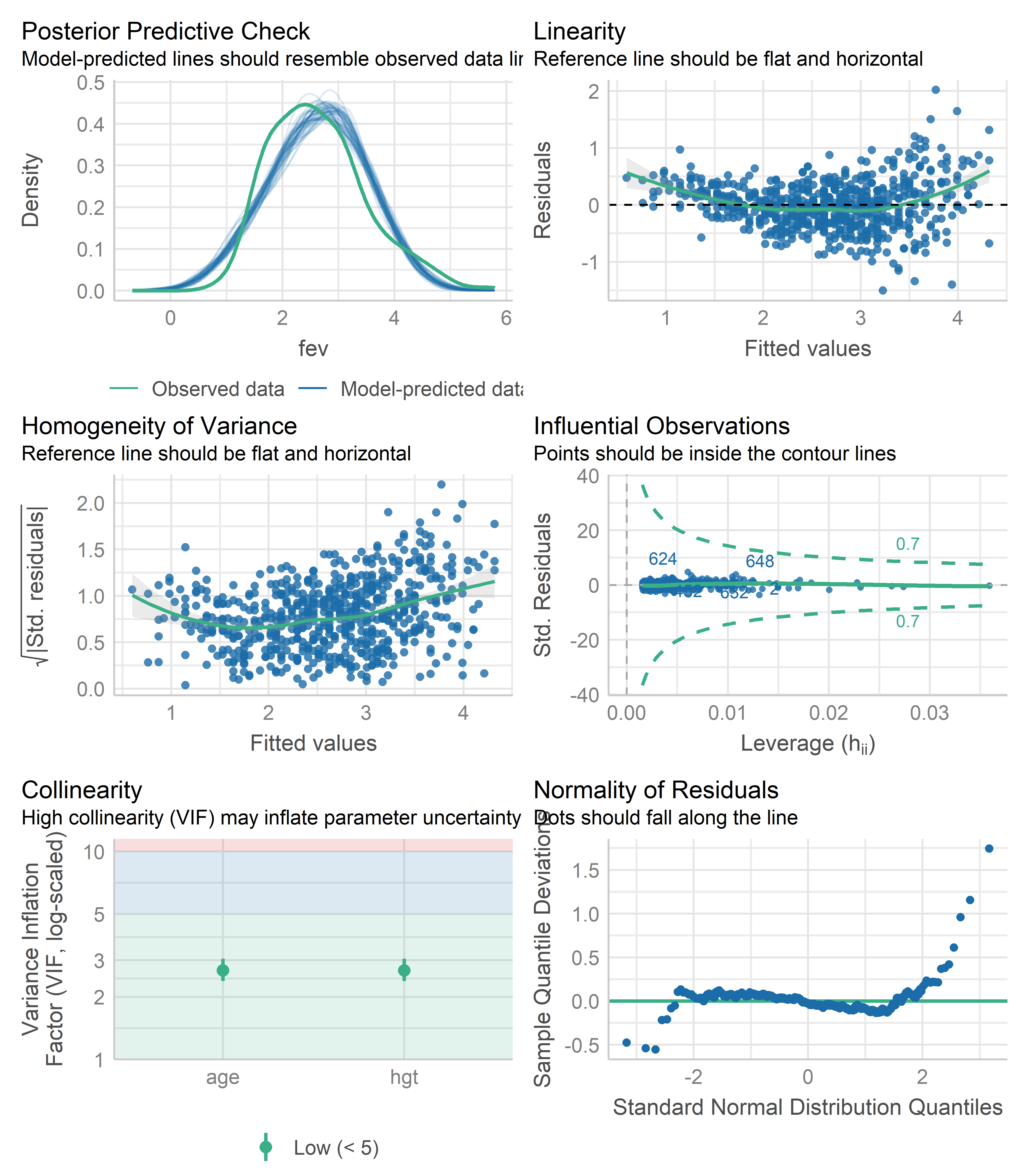
Esta función produce las mismas gráficas anteriores y dos adicionales: el Posterior Predictive Check plot, para evaluar qué tan bien el modelo predice la data observada, y el Collinearity plot para evaluar si existe problemas de multicolinealidad entre los predictores. Además, cada gráfico incluye una breve descripción de cómo usarlos.
Podemos ver en el Posterior Predictive Check plot que existe un sesgo moderado entre las predicciones del modelo y la data observada. Por otro lado, en el Collinearity plot, los valores del factor de varianza inflada (VIF, por sus siglas en inglés) son bajos para los dos predictores. Por lo tanto, parece no haber problema de multicolinealidad. En la Sección 13.1.0.3 veremos cómo evaluar este problema con más detalle.
13.1.0.2 Gráfico parcial de residuales
Un gráfico parcial de residuales nos permite evaluar si la relación funcional entre un predictor y la respuesta está correctamente representada en el modelo dada la presencia de otros predictores en el modelo. Este gráfico es más apropiado para evaluar el supuesto de linealidad de cada predictor.
Una opción para generar este gráfico en R, es usando el paquete ggeffects. Este paquete contiene una función llamada ggpredict() que produce, por defecto, valores esperados a partir de los datos usados para ajustar el modelo. En este sentido, ggpredict() es similar a las funciones estimate_expectation() o estimate_relation() del paquete modelbased.
La función ggpredict() requiere que especifiquemos el rango de valores del predictor para el cual producir los valores esperados en el parámetro terms. Para decirle que use todos los valores del predictor en la data, podemos usar la nomenclatura "x [all]". Por ejemplo, para el predictor hgt:
predicted_hgt <- ggeffects::ggpredict(fit_multiple, "hgt [all]")
predicted_hgt# Predicted values of fev
hgt | Predicted | 95% CI
------------------------------
46.00 | 0.98 | 0.83, 1.12
50.50 | 1.47 | 1.37, 1.57
54.00 | 1.85 | 1.78, 1.93
57.50 | 2.24 | 2.19, 2.28
60.50 | 2.57 | 2.53, 2.60
64.00 | 2.95 | 2.91, 2.99
67.00 | 3.28 | 3.22, 3.34
74.00 | 4.05 | 3.92, 4.17
Adjusted for:
* age = 9.93
Not all rows are shown in the output. Use `print(..., n = Inf)` to show
all rows.Luego, habiendo llamado al paquete ggeffects, podemos usar la función plot() con el argumento residuals = TRUE para generar el gráfico parcial de residuales del predictor hgt:
plot(predicted_hgt, residuals = TRUE)Data points may overlap. Use the `jitter` argument to add some amount of
random variation to the location of data points and avoid overplotting.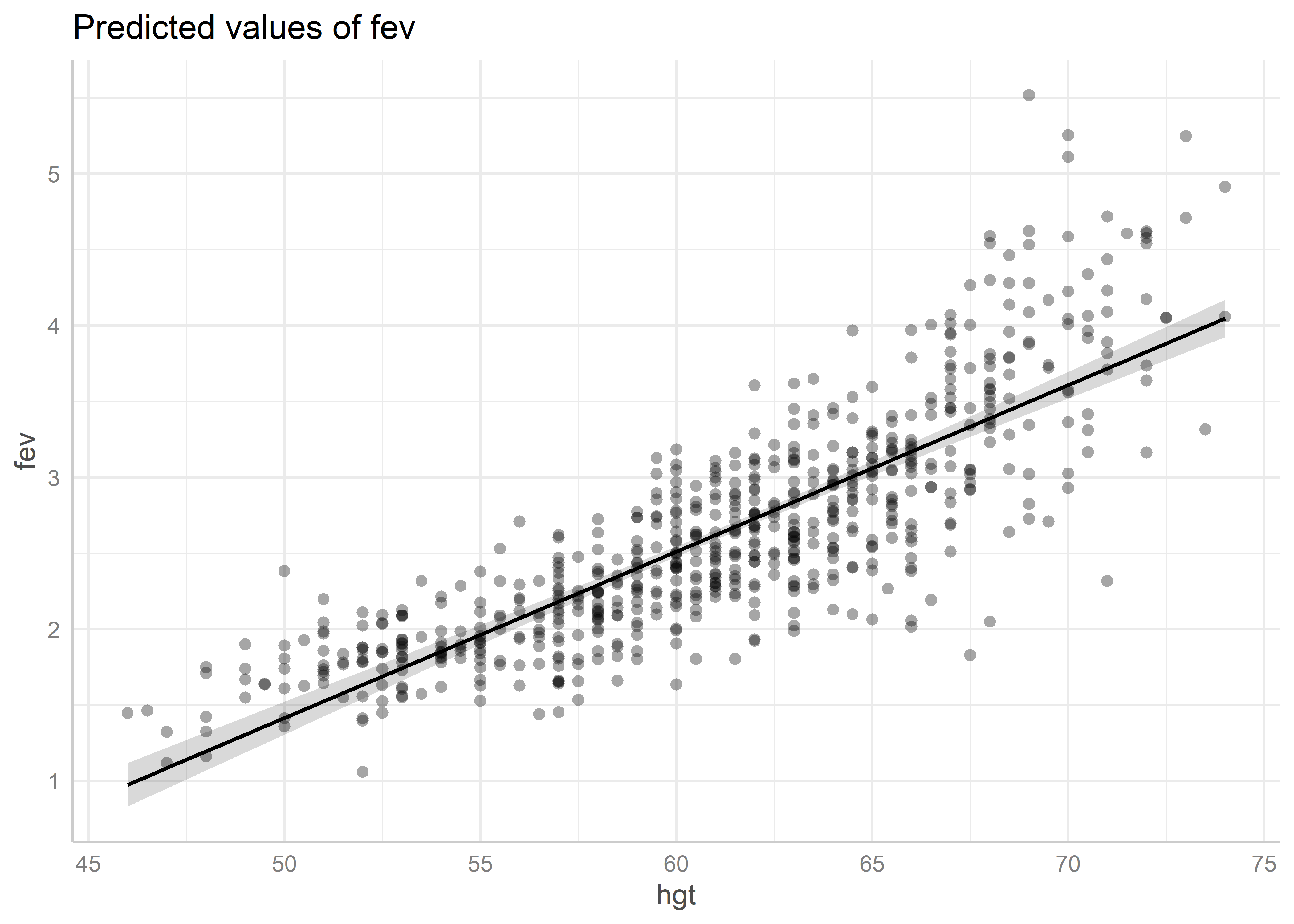
Podemos también agregar una línea de tendencia a los residuales usando el argumento residuals.line = TRUE:
plot(predicted_hgt, residuals = TRUE, residuals.line = TRUE)Data points may overlap. Use the `jitter` argument to add some amount of
random variation to the location of data points and avoid overplotting.`geom_smooth()` using formula = 'y ~ x'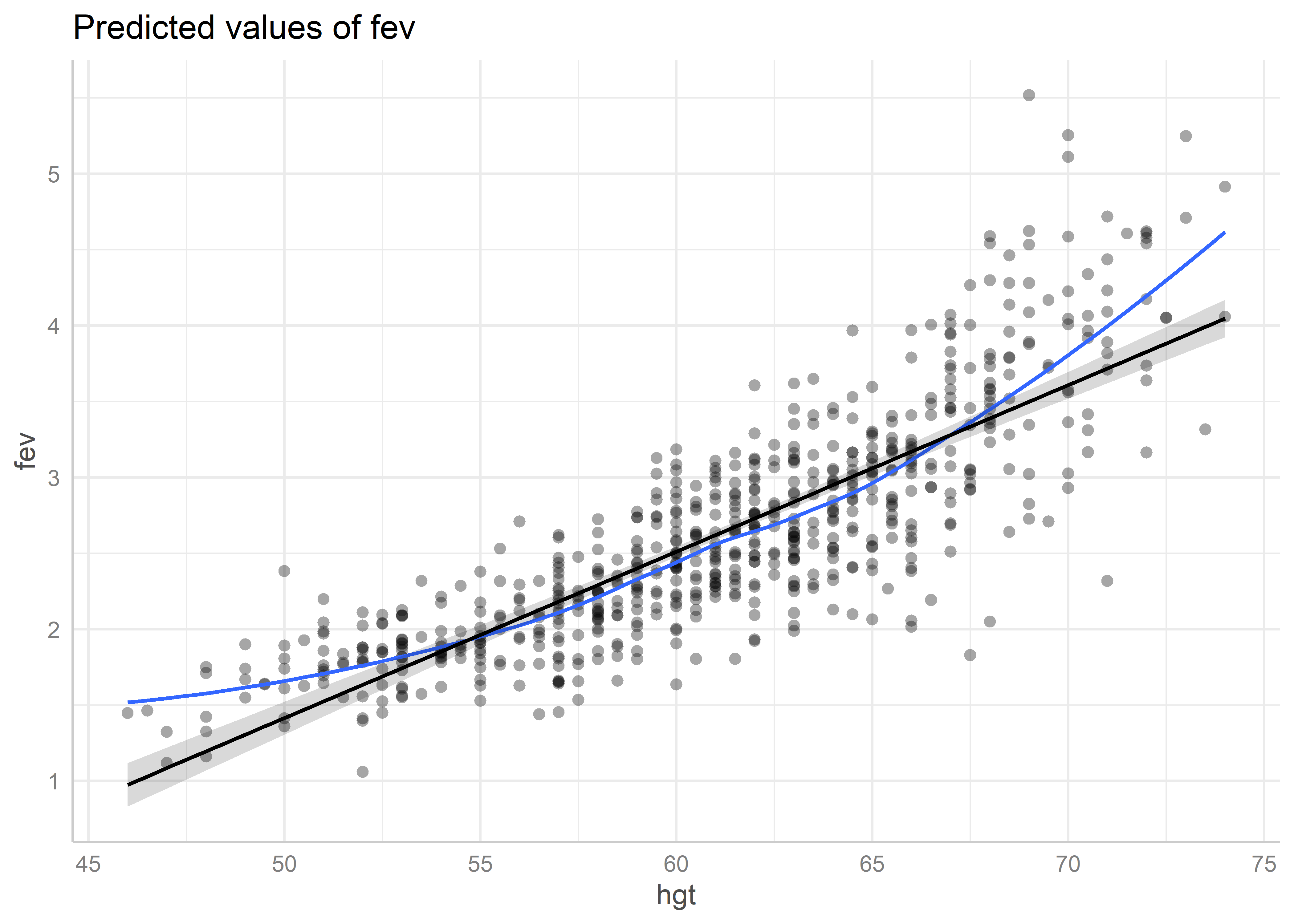
De este gráfico apreciamos que los residuales tienen un comportamiento no lineal moderado. Esto podría estar indicando que no se está cumpliendo el supuesto de linealidad para la altura.
Veamos ahora para age:
predicted_age <- ggeffects::ggpredict(fit_multiple, "age [all]")
plot(predicted_age, residuals = TRUE, residuals.line = TRUE)Data points may overlap. Use the `jitter` argument to add some amount of
random variation to the location of data points and avoid overplotting.`geom_smooth()` using formula = 'y ~ x'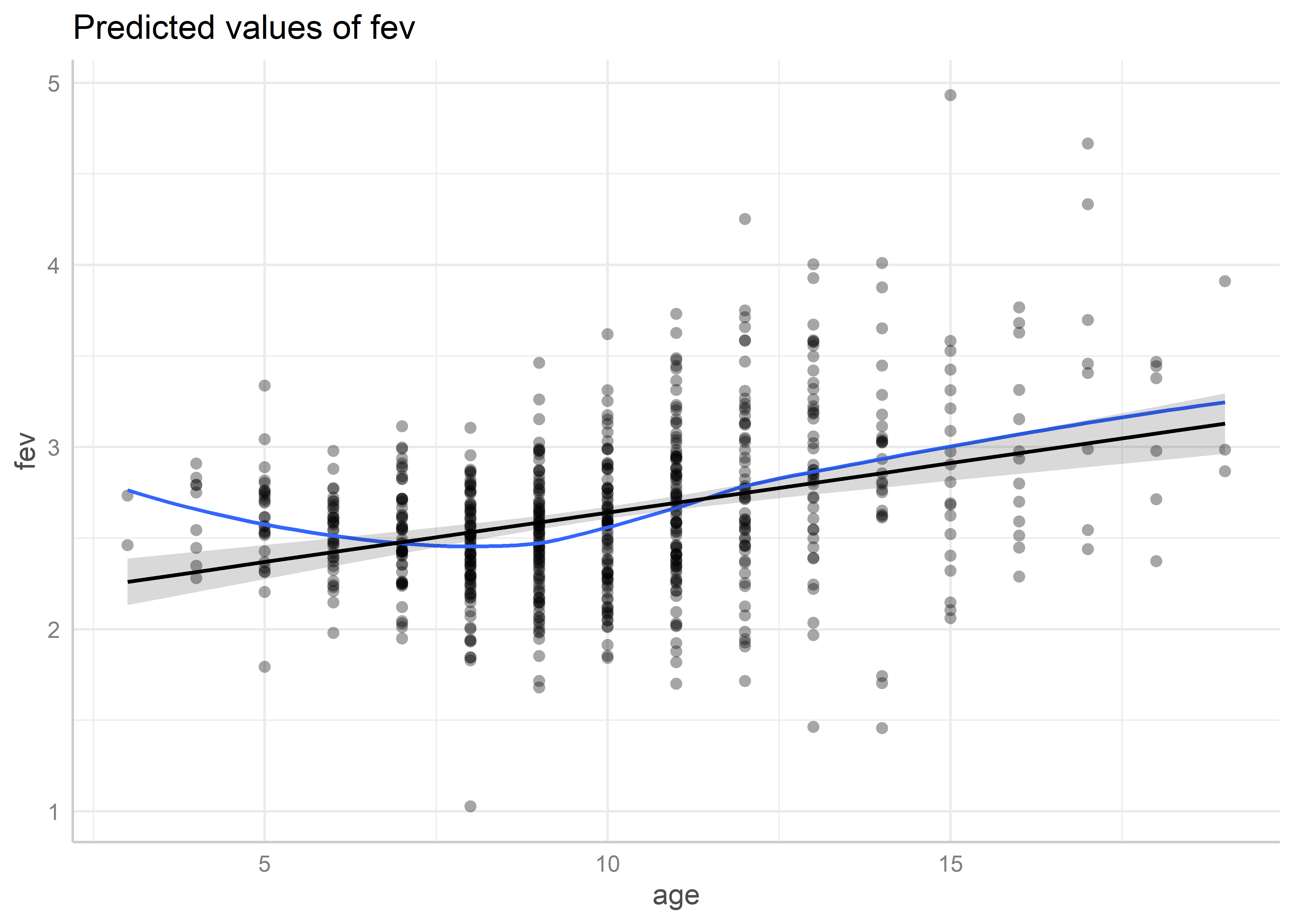
En este caso no se ve un patrón relevante.
13.1.0.3 Multicolinealidad
Para evaluar la multicolinealidad de los predictores en un modelo podemos usar la función check_collinearity() del paquete performance:
check_collinearity(fit_multiple)# Check for Multicollinearity
Low Correlation
Term VIF VIF 95% CI Increased SE Tolerance Tolerance 95% CI
hgt 2.68 [2.38, 3.05] 1.64 0.37 [0.33, 0.42]
age 2.68 [2.38, 3.05] 1.64 0.37 [0.33, 0.42]Esta función imprime una tabla con las estimaciones del VIF para cada predictor, además de los intervalos al 95% de confianza para el VIF, el incremento en el error estándar (Increased SE), la tolerancia (1/VIF) y los intervalos al 95% de confianza para la tolerancia. Esta función considera como valores aceptables del VIF los menores a 5. Un valor entre 5 a 10 puede indicar un moderado problema de multicolinealidad, mientras que un VIF mayor a 10 es señal de un problema grave de multicolinealidad.
El modelo fit_multiple parece no tener problemas de multicolinealidad. Por otro lado, hay que tener cuidado al analizar la multicolinealidad de modelos con interacción. Debido a que los predictores se usan más de una vez en estos modelos para incluir la interacción, es evidente que los términos van a tener un alto grado de colinealidad. Esto no quiere decir que el modelo esté mal especificado. Por ejemplo, con el modelo con interacción en la altura y la edad:
fit_interact_continuous <- lm(fev ~ hgt*age, data = fev)
check_collinearity(fit_interact_continuous)Model has interaction terms. VIFs might be inflated.
You may check multicollinearity among predictors of a model without
interaction terms.# Check for Multicollinearity
High Correlation
Term VIF VIF 95% CI Increased SE Tolerance Tolerance 95% CI
hgt 10.21 [ 8.85, 11.81] 3.20 0.10 [0.08, 0.11]
age 113.12 [ 97.27, 131.59] 10.64 8.84e-03 [0.01, 0.01]
hgt:age 164.66 [141.55, 191.57] 12.83 6.07e-03 [0.01, 0.01]La función nos dice que los VIF pueden estar inflados por la presencia del término de interacción, por lo que estos resultados pueden ser engañosos.
13.2 Transformaciones
Transformar la variable de respuesta puede resolver problemas de heterocedasticidad o varianza no constante, linealidad o normalidad de errores. Algunas de las transformaciones más comunes son la transformación logarítmica, raíz cuadrada o inversa. Por ejemplo, ajustemos un modelo con el volumen espiratorio forzado en escala logarítmica y la altura y la edad como predictores:
Call:
lm(formula = log(fev) ~ hgt + age, data = fev)
Residuals:
Min 1Q Median 3Q Max
-0.64994 -0.08310 0.01055 0.09324 0.42156
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.971147 0.078332 -25.16 < 2e-16 ***
hgt 0.043991 0.001647 26.71 < 2e-16 ***
age 0.019816 0.003181 6.23 8.35e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1466 on 651 degrees of freedom
Multiple R-squared: 0.8071, Adjusted R-squared: 0.8065
F-statistic: 1362 on 2 and 651 DF, p-value: < 2.2e-16Veamos los gráficos de residuales:
autoplot(fit_log)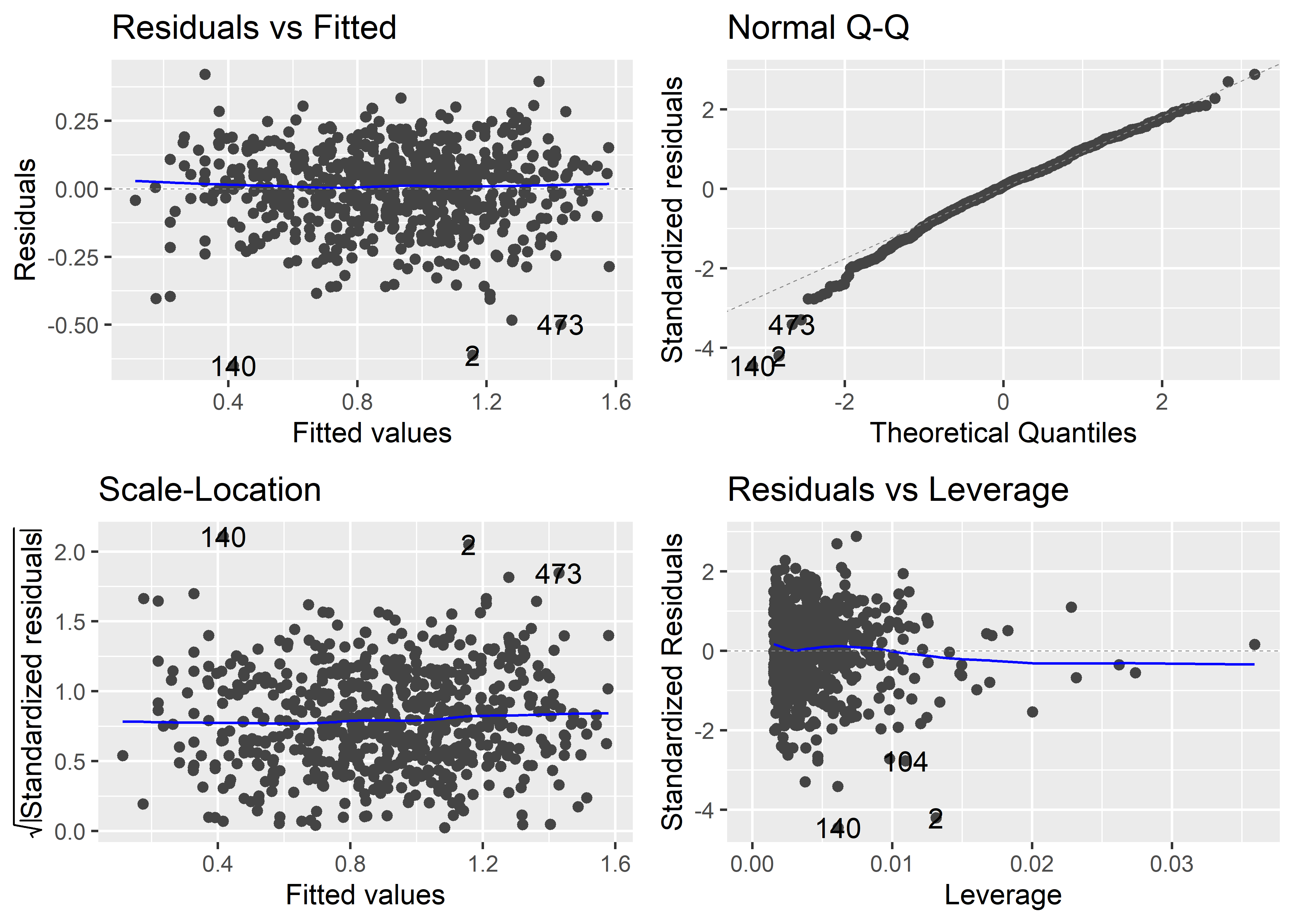
En los gráficos Residuals vs adjusted y Scale-Location vemos que los residuales parecen distribuirse homogéneamente a lo largo del eje de valores ajustados, por lo cual podemos asumir que se está cumpliendo el supuesto de homogeneidad de varianza. Estos resultados contrastan con los encontrados usando el modelo sin transformación, para el cual parecía que este supuesto no se cumplía según el análisis de los mismos gráficos.
Una forma analítica de saber qué transformación usar es usando la transformación de Box-Cox. Este método estima un parámetro que define la transformación a partir de los datos usados en el modelo. En R, el método de Box-Cox para modelos de regresión lineal está implementado en la función boxcox() del paquete MASS (este paquete viene por defecto con R). Por ejemplo, usando el modelo fev_multiple sin transformación:
boxcox(fit_multiple)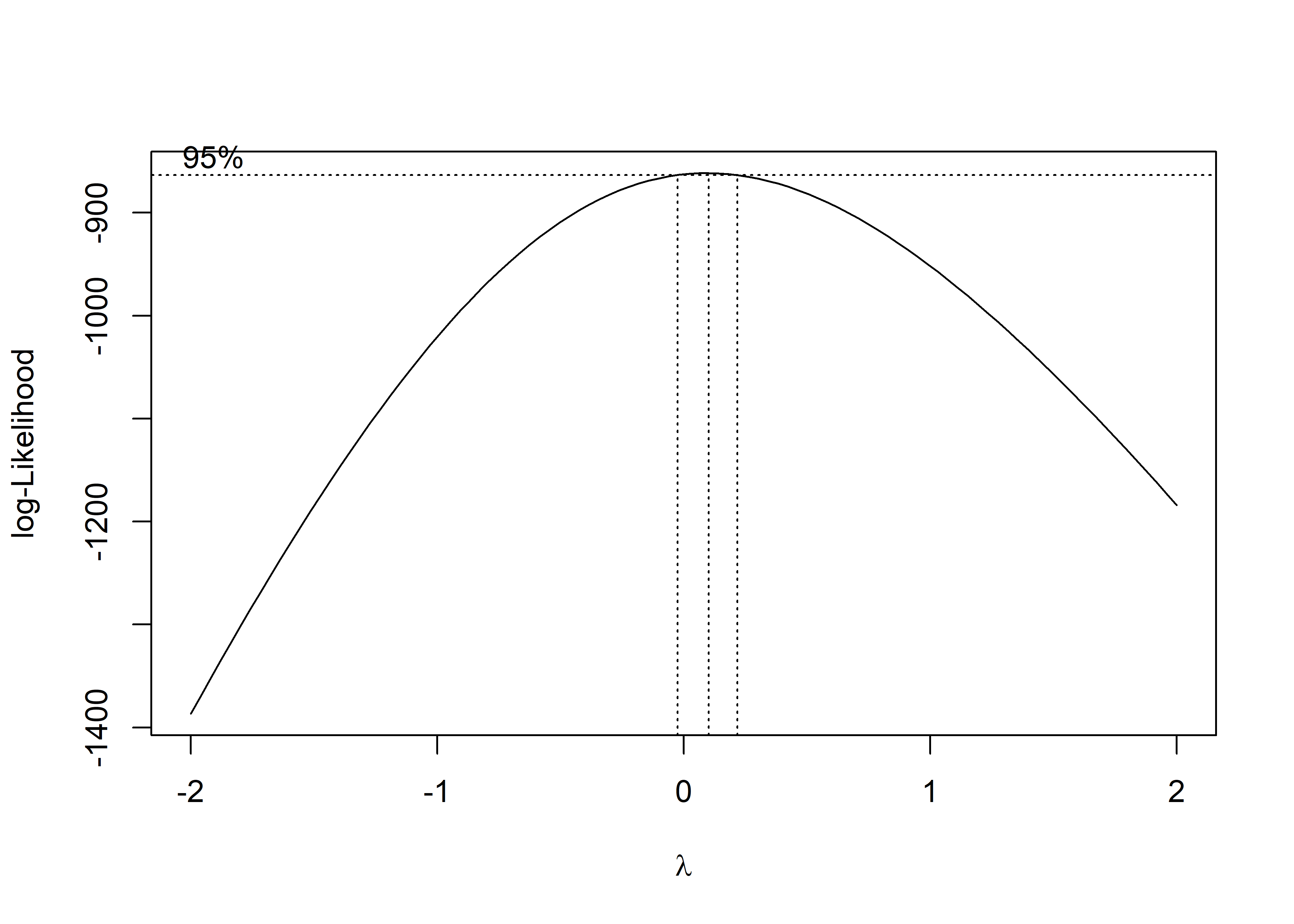
Esta función devuelve, por defecto, un gráfico con la estimación del parámetro de transformación
-
1/y^2si el intervalo incluye a -2. -
1/ysi el intervalo incluye a -1. -
1/sqrt(y)si el intervalo incluye a -2. -
log(y)si el intervalo incluye a 0. -
sqrt(y)si el intervalo incluye a 0.5. - No transformar si el intervalo incluye a 1.
-
y^2si el intervalo incluye a 2.
Para recuperar el valor óptimo del parámetro, podemos usar los siguientes comandos:
fit_boxcox <- boxcox(fit_multiple, plotit = FALSE)
lambda_opt<- fit_boxcox$x[which.max(fit_boxcox$y)]
lambda_opt[1] 0.1Para este caso, podríamos transformar la variable de respuesta usando y^0.1. Sin embargo, esta transformación no es muy intuitiva y por eso se recomienda usar la transformación más cercana, la transformación logarítmica.
El mayor inconveniente de usar una transformación es que la interpretación que se haga de los resultados del modelo se harían sobre la nueva escala de la variable de respuesta, no sobre la original. Por ejemplo, si usamos la transformación logarítmica como en fit_log, tendríamos que interpretar el modelo sobre el logaritmo del volumen espiratorio forzado.
13.3 Regresión polinomial
En el caso que se sospeche que la asociación entre la respuesta y un predictor es no lineal, podemos transformar el predictor de manera que esta asociación sea capturada en el modelo de regresión. La técnica más básica para incluir asociaciones no lineales de predictores es incluyendo los términos polinomiales de grado mayor a cero de un predictor en el modelo. Por ejemplo, el polinomio de orden 2 de la variable
Para incluir polinomios de un predictor en un modelo de regresión usamos la función poly(). Con el parámetro degree de esta función especificamos el grado del polinomia. Vimos de los gráficos parciales de residuales que la altura parece tener una asociación no lineal con el volumen espiratorio forzado bajo el modelo. Probemos agregando un polinomio de grado 2 sobre la altura:
Call:
lm(formula = fev ~ poly(hgt, degree = 2) + age, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.65645 -0.23224 0.00792 0.23676 1.88121
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.050814 0.087580 23.416 < 2e-16 ***
poly(hgt, degree = 2)1 15.707879 0.654504 24.000 < 2e-16 ***
poly(hgt, degree = 2)2 3.344727 0.399952 8.363 3.73e-16 ***
age 0.059003 0.008678 6.799 2.38e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3991 on 650 degrees of freedom
Multiple R-squared: 0.7891, Adjusted R-squared: 0.7881
F-statistic: 810.7 on 3 and 650 DF, p-value: < 2.2e-16Veamos los gráficos de residuales de este modelo:
autoplot(fit_poly)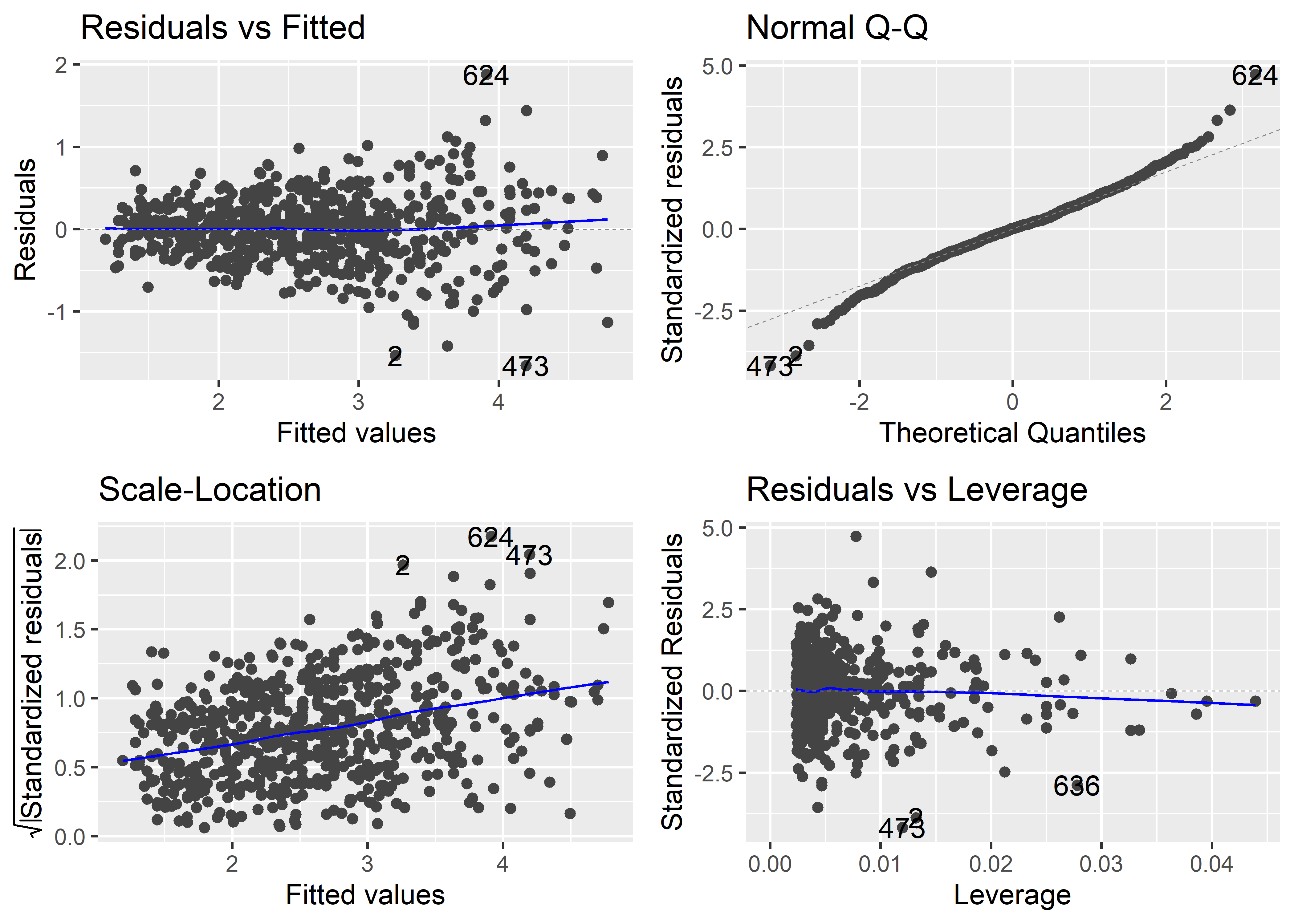
Vemos en los gráficos Residuals vs Fitted y Scale-Location que el patrón no-lineal que tenían los residuales se alivió; sin embargo, todavía se aprecia un problema moderado de heterocedasticidad.
Revisamos los gráficos parciales de residuales. Primero para hgt:
predicted_hgt_poly <- ggeffects::ggpredict(fit_poly, "hgt [all]")
plot(predicted_hgt_poly, residuals = TRUE, residuals.line = TRUE)Data points may overlap. Use the `jitter` argument to add some amount of
random variation to the location of data points and avoid overplotting.`geom_smooth()` using formula = 'y ~ x'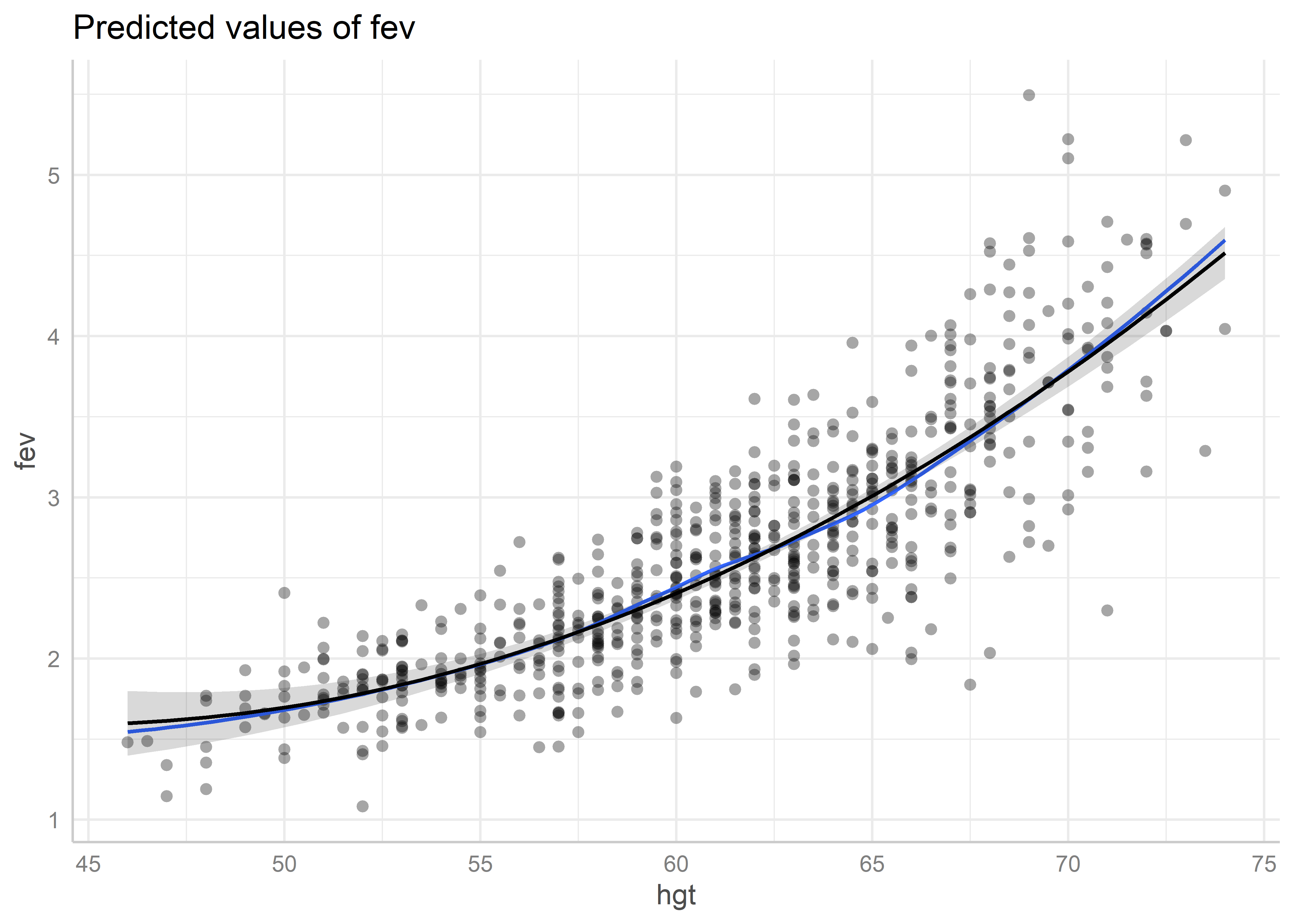
Vemos que ahora sí la asociación entre el volumen espiratorio y la altura parece estar correctamente especificada en el modelo. Ahora para age:
predicted_age_poly <- ggeffects::ggpredict(fit_poly, "age [all]")
plot(predicted_age_poly, residuals = TRUE, residuals.line = TRUE)Data points may overlap. Use the `jitter` argument to add some amount of
random variation to the location of data points and avoid overplotting.`geom_smooth()` using formula = 'y ~ x'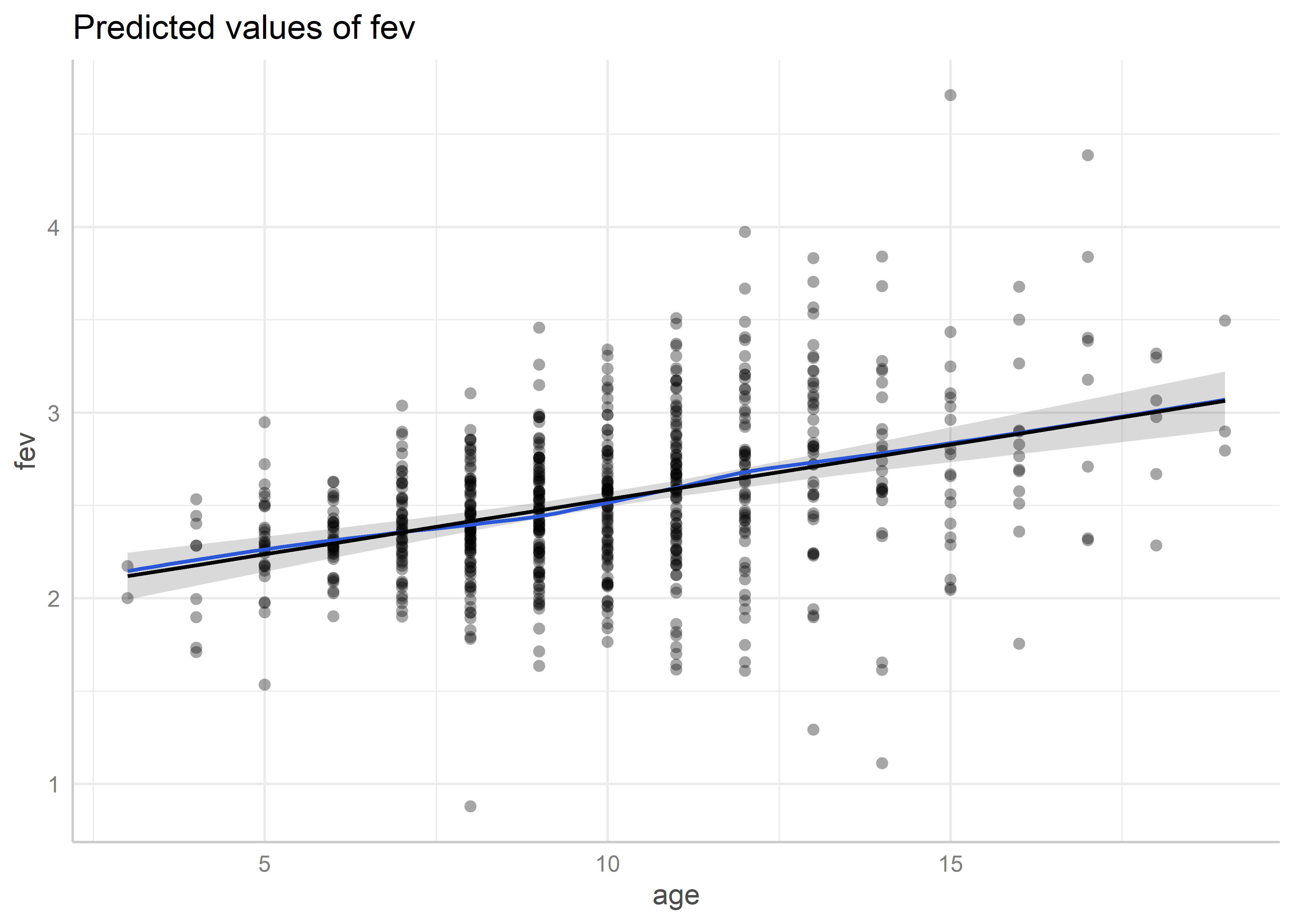
Para la edad también parece que su efecto está correctamente especificado.
Si quisiéramos agregar solo el término cuadrático hgt^2, necesitamos incluir esta expresión dentro de la función I(). Esta función evalúa de manera literal el operador de exponenciación ^:
Call:
lm(formula = fev ~ I(hgt^2) + age, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.53719 -0.24337 -0.00406 0.24736 1.98068
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.356e+00 9.222e-02 -14.702 < 2e-16 ***
I(hgt^2) 9.225e-04 3.771e-05 24.465 < 2e-16 ***
age 5.175e-02 8.829e-03 5.862 7.29e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.41 on 651 degrees of freedom
Multiple R-squared: 0.7771, Adjusted R-squared: 0.7764
F-statistic: 1135 on 2 and 651 DF, p-value: < 2.2e-16Veamos los gráficos de residuales:
autoplot(fit_poly_2)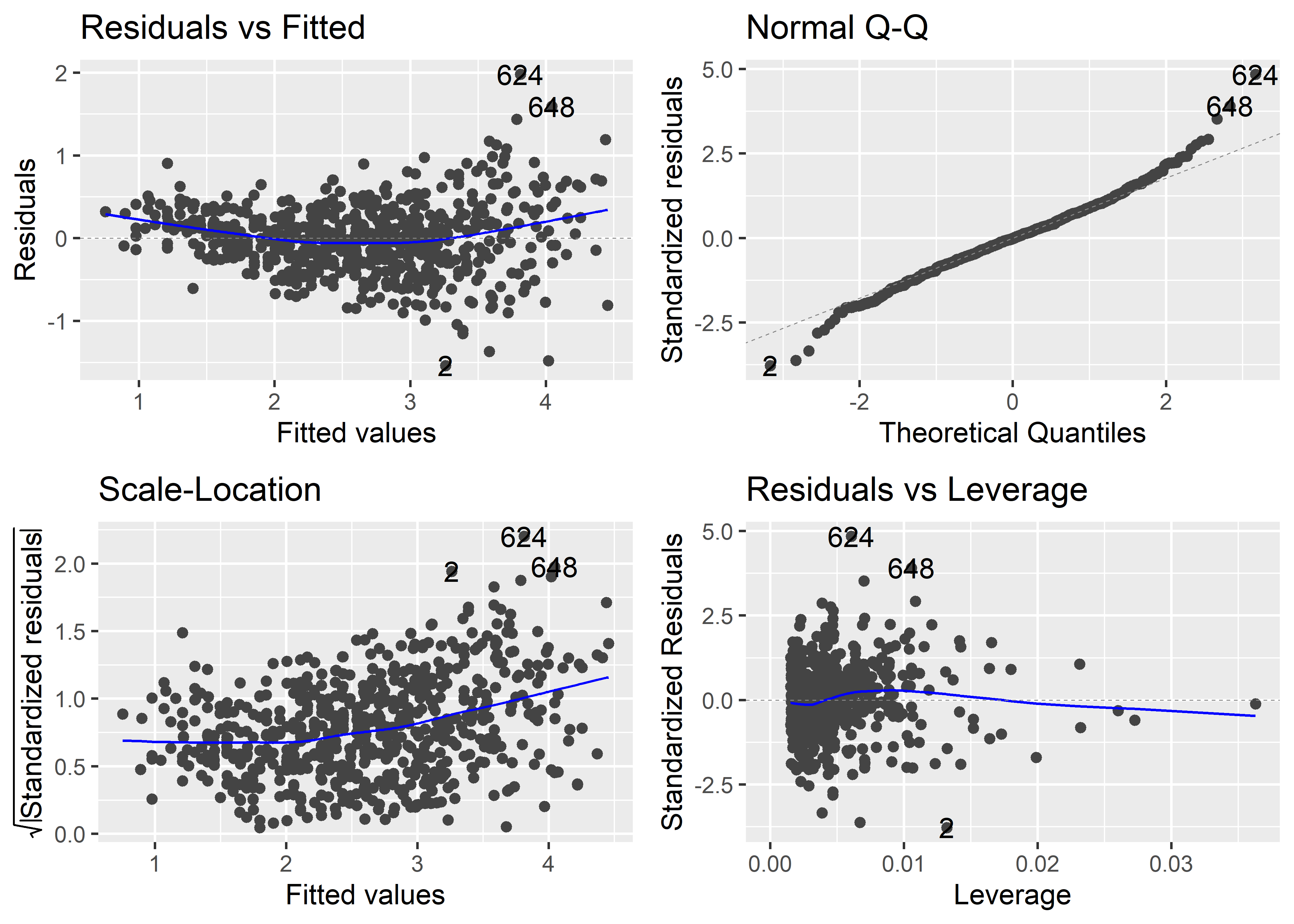
Al parecer, incluir solo el término cuadrático no ayuda a mejorar el patrón no lineal de los residuales. Esto se debe a que son los polinomios completos los que matemáticamente se usan para aproximar funciones no lineales, no los términos por separado.
13.4 Evaluación de modelos
En esta sección veremos algunas herramientas en R para evaluar un conjunto de modelos usando medidas estadísticas de bondad de ajuste.
13.4.1 Usando la función summary()
La función summary() nos devuelve algunas medidas de bondad de ajuste. Veamos para el modelo fit_multiple:
summary(fit_multiple)
Call:
lm(formula = fev ~ hgt + age, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.50533 -0.25657 -0.01184 0.24575 2.01914
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.610466 0.224271 -20.558 < 2e-16 ***
hgt 0.109712 0.004716 23.263 < 2e-16 ***
age 0.054281 0.009106 5.961 4.11e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4197 on 651 degrees of freedom
Multiple R-squared: 0.7664, Adjusted R-squared: 0.7657
F-statistic: 1068 on 2 and 651 DF, p-value: < 2.2e-16La función summary() devuelve todos los resultados que se imprimen en objetos separados. Para acceder a ellos podemos usar el operador $. Por ejemplo, en primera instancia tenemos el Residual standard error (RSE) o error estándar residual. Para extraer el valor del RSE:
summary(fit_multiple)$sigma[1] 0.4197046También tenemos al Multiple R-squared, también conocido como el coeficiente de determinación:
summary(fit_multiple)$r.squared[1] 0.7664081Por último, el Adjusted R-squared o coeficiente de determinación ajustado:
summary(fit_multiple)$adj.r.squared[1] 0.7656905Para ver la lista completa de objetos que devuelve la función summary() para el modelo fit_multiple podemos usar la función names():
13.4.2 Criterio de información de Akaike
El criterio de información de Akaike o AIC (por sus siglas en inglés) puede ser calculado usando la función AIC():
AIC(fit_multiple)[1] 725.3535También podemos calcular una variante conocida como el criterio de información Bayesiano o BIC (por sus siglas en inglés):
BIC(fit_multiple)[1] 743.285913.4.3 Múltiples medidas
El paquete performance tiene una función llamada model_performance() que permite calcular diferentes indicadores de bondad de ajuste. Por ejemplo, para el modelofit_multiple:
model_performance(fit_multiple)# Indices of model performance
AIC | AICc | BIC | R2 | R2 (adj.) | RMSE | Sigma
---------------------------------------------------------------
725.354 | 725.415 | 743.286 | 0.766 | 0.766 | 0.419 | 0.420Para modelos de regresión lineal, esta función calcula el AIC, el AIC con correción por muestra pequeña (AICc), el coeficiente de determinación (R2), el coeficiente de determinación ajustado (R2 (adj.)), la raíz cuadrada del error cuadrático medio (RMSE) y la desviación estándar residual (Sigma).
Los indicadores para un solo modelo no tienen mucho sentido si no se comparan. Para comparar diferentes modelos, podemos usar la función compare_performance(). Por ejemplo, comparemos el modelo de regresión simple con la altura (fit_simple), el modelo de regresión múltiple con la altura y la edad(fit_multiple) y el modelo de regresión múltiple con los términos polinomiales para la altura (fit_poly):
fit_simple <- lm(fev ~ hgt, fev)
compare_performance(fit_simple, fit_multiple, fit_poly)# Comparison of Model Performance Indices
Name | Model | AIC (weights) | AICc (weights) | BIC (weights) | R2 | R2 (adj.) | RMSE | Sigma
---------------------------------------------------------------------------------------------------------
fit_simple | lm | 758.1 (<.001) | 758.1 (<.001) | 771.6 (<.001) | 0.754 | 0.753 | 0.430 | 0.431
fit_multiple | lm | 725.4 (<.001) | 725.4 (<.001) | 743.3 (<.001) | 0.766 | 0.766 | 0.419 | 0.420
fit_poly | lm | 660.5 (>.999) | 660.6 (>.999) | 682.9 (>.999) | 0.789 | 0.788 | 0.398 | 0.399Podemos ver que de estos modelos, el modelo de regresión múltiple con el polinomio de segundo grado para la altura es el modelo que tiene mejores valores para las medidas de bondad de ajuste. Esta función también permite crear un ranking ponderado de estas medidas. Para esto, debemos agregar el argumento rank = TRUE:
compare_performance(fit_simple, fit_multiple, fit_poly, rank = TRUE)# Comparison of Model Performance Indices
Name | Model | R2 | R2 (adj.) | RMSE | Sigma | AIC weights | AICc weights | BIC weights | Performance-Score
-----------------------------------------------------------------------------------------------------------------------
fit_poly | lm | 0.789 | 0.788 | 0.398 | 0.399 | 1.000 | 1.000 | 1.000 | 100.00%
fit_multiple | lm | 0.766 | 0.766 | 0.419 | 0.420 | 8.35e-15 | 8.48e-15 | 7.86e-14 | 20.20%
fit_simple | lm | 0.754 | 0.753 | 0.430 | 0.431 | 6.44e-22 | 6.62e-22 | 5.70e-20 | 0.00%Con rank = TRUE se crea una nueva columna Performance-Score que se utiliza para rankear a los modelos.
13.5 Modelos anidados
Los modelos anidados son aquellos que están contenidos dentro de otros en relación a sus términos. Por ejemplo, el modelo fit_poly contiene a fit_multiple y este contiene a fit_simple. Para evaluar la significancia de una secuencia de modelos anidados, podemos usar la función anova(), la cual genera una tabla de análisis de varianza. Esta función compara los modelos entre sí en el orden en el que se han ingresado. Para modelos anidados, ingresamos los modelos empezando por el que está contenido en todos hasta el que contiene a todos:
anova(fit_simple, fit_multiple, fit_poly)Analysis of Variance Table
Model 1: fev ~ hgt
Model 2: fev ~ hgt + age
Model 3: fev ~ poly(hgt, degree = 2) + age
Res.Df RSS Df Sum of Sq F Pr(>F)
1 652 120.93
2 651 114.67 1 6.2591 39.295 6.640e-10 ***
3 650 103.53 1 11.1398 69.937 3.731e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Esta función compara fit_multiple sobre fit_simple y fit_poly sobre fit_multiple. De este resultado podemos concluir que el modelo fit_multiple es significativo sobre el modelo fit_simple y el modelo fit_poly es significativo sobre el modelo fit_multiple.
13.6 Algoritmos de selección de modelos
En esta sección, veremos algunos algoritmos en R para la búsqueda del mejor subconjunto de predictores de un modelo de regresión lineal.
13.6.1 Mejor subconjunto
El algoritmo de mejor subconjunto o best subset consiste en elegir la mejor combinación de predictores para cada tamaño de subconjunto de estos. Para este fin, podemos usar la función regsubsets() del paquete leaps. Para cada tamaño de subconjunto, este función selecciona el modelo que minimiza la suma residual de cuadrados, o que en su defecto maximiza el coeficiente de determinación
Con esta función se puede hacer cuatro tipos de búsquedas: búsqueda exhaustiva, búsqueda hacia adelante, búsqueda hacia atrás o reemplazo secuencial. Podemos especificar el tipo de búsqueda usando el parámetro method con los valores "exhaustive" para la búsqueda exhaustiva, "forward" para la búsqueda hacia adelante, "backward" para la búsqueda hacia atrás, y "seqrep" para el reemplazo secuencial.
Tenemos que pasar a la función la fórmula del modelo que incluya todos los predictores que queremos evaluar. Probaremos con el modelo que incluye el polinomio de segundo grado para la altura, la edad y el sexo para que el algoritmo evalúe las combinaciones de todos estos términos. Por ejemplo, haciendo una búsqueda exhaustiva:
library(leaps)best_subsets_exhaustive <- regsubsets(
fev ~ poly(hgt, 2) + age + sex, data = fev, method = "exhaustive"
)
summary(best_subsets_exhaustive)Subset selection object
Call: regsubsets.formula(fev ~ poly(hgt, 2) + age + sex, data = fev,
method = "exhaustive")
4 Variables (and intercept)
Forced in Forced out
poly(hgt, 2)1 FALSE FALSE
poly(hgt, 2)2 FALSE FALSE
age FALSE FALSE
sex FALSE FALSE
1 subsets of each size up to 4
Selection Algorithm: exhaustive
poly(hgt, 2)1 poly(hgt, 2)2 age sex
1 ( 1 ) "*" " " " " " "
2 ( 1 ) "*" "*" " " " "
3 ( 1 ) "*" "*" "*" " "
4 ( 1 ) "*" "*" "*" "*"De estos resultados, podemos ver que el mejor modelo con un predictor es el que incluye a hgt, el mejor modelo de dos predictores incluye a los términos polinomiales de hgt, el mejor modelo de 3 predictores incluye el polinomio de la altura y a la edad, y por último tenemos al modelo con todos los predictores.
Para pasar los resultados a un data frame podemos usar la función tidy() del paquete broom:
# A tibble: 4 × 9
`(Intercept)` `poly(hgt, 2)1` `poly(hgt, 2)2` age sex r.squared
<lgl> <lgl> <lgl> <lgl> <lgl> <dbl>
1 TRUE TRUE FALSE FALSE FALSE 0.754
2 TRUE TRUE TRUE FALSE FALSE 0.774
3 TRUE TRUE TRUE TRUE FALSE 0.789
4 TRUE TRUE TRUE TRUE TRUE 0.792
# ℹ 3 more variables: adj.r.squared <dbl>, BIC <dbl>, mallows_cp <dbl>Esta tabla también nos devuelve el
best_subsets_exhaustive %>%
tidy() %>%
mutate(id = row_number()) %>%
ggplot(aes(x = id, y = BIC)) +
geom_line()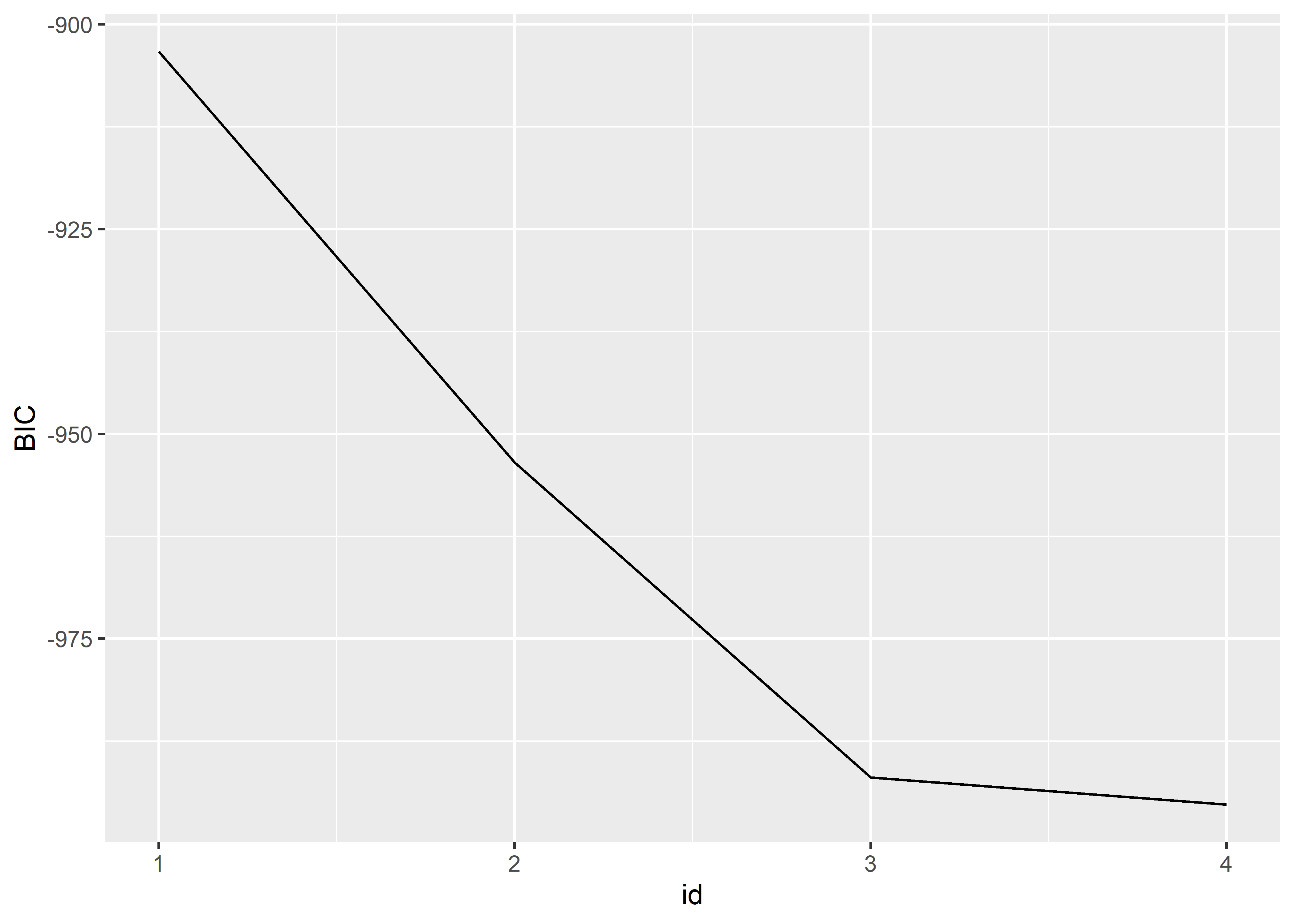
Según este gráfico, el modelo con todos los predictores ofrece mejor ajuste con respecto al BIC. Sin embargo, la mejora que ofrece este modelo con respecto al de 3 predictores es mínima. Por parsimonia, nos podríamos quedar con el mejor modelo de 3 predictores que incluye al polinomio de la altura y a la edad.
13.6.2 Selección por pasos con stepAIC()
La función stepAIC() del paquete MASS realiza selección por pasos sin considerar tamaños de subconjunto. Es decir, empieza con el modelo nulo o completo y va agregando o eliminando predictores sin seleccionar el mejor para los diferentes tamaños de subconjuntos de estos. Este algoritmo es mucho más rápido que el de regsubset(). Sin embargo, la desventaja es que stepAIC() busca sobre un rango menor de posibles modelos.
Esta función utiliza el AIC como criterio para agregar o eliminar predictores en cada paso. Se puede hacer tres tipos de búsquedas: hacia adelante, hacia atrás, y en ambas direcciones. Podemos definir la dirección de búsqueda con el parámetro direction y pasando el valor "forward" para la búsqueda hacia adelante, "backward" para la búsqueda hacia atrás, y "both" para la búsqueda en ambas direcciones.
stepAIC() tiene dos parámetros importantes: object y scope. En object pasamos el modelo a partir del cual se iniciará la búsqueda y en scope pasamos el rango de modelos que queremos evaluar usando la notación de fórmula. scope pude ser una lista con dos términos: lower para especificar el mínimo modelo posible y upper para especificar el máximo modelo posible.
Por ejemplo, si queremos hacer una búsqueda en ambas direcciones tomando como modelo inicial fit_simple y buscando entre el modelo sin predictores (fev ~ 1) y el modelo que incluye todas las interacciones entre la altura, la edad y el sexo (fev ~ hgt*age*sex) usaríamos el siguiente comando:
fit_step <- stepAIC(
object = fit_multiple,
scope = list(lower = fev ~ 1, upper = fev ~ hgt*age*sex),
direction = "both"
)Start: AIC=-1132.62
fev ~ hgt + age
Df Sum of Sq RSS AIC
+ hgt:age 1 11.516 103.16 -1199.83
+ sex 1 4.027 110.65 -1154.00
<none> 114.67 -1132.62
- age 1 6.259 120.93 -1099.86
- hgt 1 95.326 210.00 -738.94
Step: AIC=-1199.83
fev ~ hgt + age + hgt:age
Df Sum of Sq RSS AIC
+ sex 1 1.7587 101.40 -1209.1
<none> 103.16 -1199.8
- hgt:age 1 11.5164 114.67 -1132.6
Step: AIC=-1209.08
fev ~ hgt + age + sex + hgt:age
Df Sum of Sq RSS AIC
+ hgt:sex 1 1.4618 99.938 -1216.6
+ age:sex 1 1.1472 100.253 -1214.5
<none> 101.400 -1209.1
- sex 1 1.7587 103.159 -1199.8
- hgt:age 1 9.2481 110.648 -1154.0
Step: AIC=-1216.58
fev ~ hgt + age + sex + hgt:age + hgt:sex
Df Sum of Sq RSS AIC
<none> 99.938 -1216.6
+ age:sex 1 0.0558 99.882 -1214.9
- hgt:sex 1 1.4618 101.400 -1209.1
- hgt:age 1 5.8118 105.750 -1181.6Por defecto, la función imprime información sobre qué predictores o términos han sido añadidos o eliminados en cada paso y algunas medidas estadísticas y de bondad de ajuste, incluyendo el AIC, de los modelos evaluados.
A diferencia de la función regsubsets(), la función stepAIC() sí devuelve el modelo seleccionado. Para ver los resultados del ajuste usamos la función summary():
summary(fit_step)
Call:
lm(formula = fev ~ hgt + age + sex + hgt:age + hgt:sex, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.38393 -0.22870 0.00734 0.22444 1.74894
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.6352203 0.5132763 -1.238 0.21632
hgt 0.0426603 0.0087813 4.858 1.49e-06 ***
age -0.3047092 0.0611473 -4.983 8.03e-07 ***
sex -1.0346254 0.3728293 -2.775 0.00568 **
hgt:age 0.0058292 0.0009496 6.139 1.45e-09 ***
hgt:sex 0.0189534 0.0061564 3.079 0.00217 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3927 on 648 degrees of freedom
Multiple R-squared: 0.7964, Adjusted R-squared: 0.7949
F-statistic: 507 on 5 and 648 DF, p-value: < 2.2e-16Podemos ver que según este algoritmo y los parámetros de búsqueda, el modelo que brinda un mejor AIC es aquel que incluye a la altura, la edad, el sexo, y las interacciones de segundo orden entre la altura y la edad, y la altura y el sexo.
13.7 Ejercicios
Para estos ejercicios usaremos el archivo de datos iq.csv presentado en la sección de ejercicios del Capítulo 12.
Ejercicio 1
Realizar el análisis de residuales para el chequeo de la adecuación del modelo de regresión lineal múltiple para los puntajes de la prueba cognitiva de los niños con el puntaje de la madre y la variable indicadora de si la madre se graduó o no de la secundaria como predictores.
Ejercicio 2
Reemplazar en el modelo anterior el término lineal del puntaje de la madre por un polinomio de grado 2 para este predictor. Chequear la adecuación del modelo.
Ejercicio 3
Realizar la evaluación del ajuste de los modelos para los puntajes de la prueba cognitiva de los niños usando el puntaje de la madre y la variable indicadora de si la madre se graduó o no de la secundaria como predictores. Construir los modelos de regresión lineal simple y múltiple, y con y sin interacción para el último caso.