26 Diseños cuasi-experimentales
26.1 General
En la evaluacion de intervenciones, se busca saber si la intervención efectivamente causó algún cambio significativo en alguna caracteristica de una poblacion determinada (por ejemplo, la tasa de mortalidad por dengue en una comunidad). Para ello lo mejor seria llevar a cabo un experimento controlado aleatorizado, pues lo que hace que un experimento tenga el poder de medir correctamente el impacto de una variable sobre otra es la aleatorización en la selección de la muestra del estudio (control) y en la aleatorización del tratamiento (intervencion), bajo el control de un investigador.
Llevar a cabo un experimento aleatorio muchas veces no es factible; sin embargo, aún asi se puede analizar el impacto de una intervención via un experimento natural, también conocido como diseño cuasiexperimental, los cuales valiendose de determinados supuestos buscan replicar los resultados de los experimentos aleatorizados.
Un experimento natural se caracteriza principalmente por que no hay asignación aleatoria, asi a diferencia de un experimento controlado aleatorio, en un experimento natural no hay asignación aleatoria de las unidades a las intervenciones bajo la supervision de un investigador, de modo tal que variación en la variable de tratamiento es determinada por factores externos.
Entre las metodologias clasicas que pertenecen a este marco teorico son: Regresión discontinua (RD), Series de tiempo interrumpidas (ITS), Diferencia en diferencias (DD), entre otras (Kraig, 2021).
26.1.1 Paquetes
Los paquetes generales a ser utilizados en esta sección son:
26.2 Regresión discontinua (RD)
26.2.1 Descripcion general del diseño
Muchas intervenciones se valen de un indicador o score el cual al fijarse en un determinado umbral establece la condicion de eligibilidad para dicha intervencion. Por ejemplo, muchos programas sociales contra la pobreza se valen de un indicador económico para decidir la participación de sus beneficiarios en el programa.
La regresión discontinua es una metodología la cual puede ser empleada para evaluar aquellas intervenciones que tengan una regla de asignacion del tratamiento que involucre un indice de eligibilidad continuo con un umbral claramente definido. Asi dada la importacia de la regla de asignacion, esta puede ser nitida (o Sharp) o difusa (o fuzzy).
El supuesto, que se prueba como parte del procedimiento, es que las unidades cercanas a ambos lados del límite son suficientemente similares para que las excluidas de la intervención sean un grupo de comparación válido.
La diferencia en los resultados entre aquellos que están cerca de ambos lados del límite, medida por la discontinuidad en la línea de regresión en ese punto, es atribuible a la intervención, al igual que la medida del impacto de la intervención.
26.2.2 Modelo
donde :
Variables:
Parametros
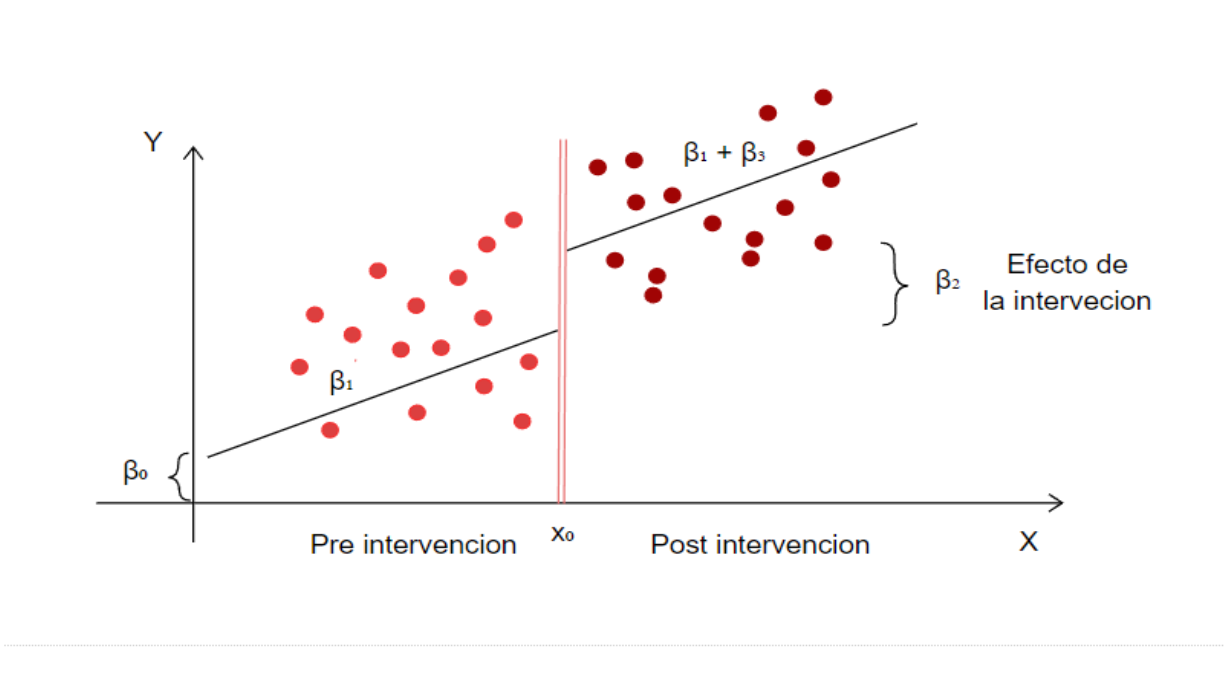
26.2.3 Supuestos
- Supuesto de continuidad (Hahn, Todd, y Van der Klaauw 2001): Las funciones de esperanza condicional son continuas (o suavizadas) en el umbral eligido, esto es:
Este supuesto es clave; sin embargo, su validacion completa no es factible en la realidad.
El indicador de eligibilidad debe ser continuo alrededor del umbral
Supuestos usuales de un modelo de regresión (Homocedasticidad, no autocorrelacion, etc) de acuerdo al caso. Debemos asegurarnos de que los efectos estimados sean insesgados y consistentes, hecha la especificación correcta del modelo.
26.2.4 Caso de estudio
Emplearemos datos de un programa social, el cual consistió en un subsidio económico para solventar parte del gasto en salud de un grupo de hogares. Al respecto la base de dato cuenta con las siguientes variables:
| Variable | Descripcion |
|---|---|
| enrolled | Participa si o no del programa social (0=no 1=si) |
| round | Etapa de la intervención (0 = Pre , 1 = Post intervención) |
| locality_identifier | Identificador de localidad geográfica a la cual pertenece el hogar |
| age_hh | Edad de la cabeza del hogar |
| indigenous | La cabeza de hogar habla un lenguaje indigena |
| educ_hh | Nivel educativo de la cabeza de hogar (Años completados de escolarizacion) |
| educ_sp | Nivel educativo de la conyuge (Años completados de escolarizacion) |
| female_hh | La cabeza de hogar es una mujer |
| dirtfloor | El hogar cuenta con un piso de tierra (0=no 1=si) |
| bathroom | El hogar cuenta con un baño privado (0=no 1=si) |
| land | Numero de hectareas de tierra pertenecientes al hogar |
| age_hh | Edad de la cabeza del hogar |
| hhsize | Numero de miembros del hogar |
| eligible | El hogar es eligible para pertenecer al programa social (0=no 1=si) |
| hospital | Visito algun miembro del hogar el hospital durante el año pasado (0=no 1=si) |
Emplearemos los datos de la intervención sobre el gasto en Salud; sin embargo, tomando en cuenta que la variable pobreza sirvió como variable scoring o running. Asi se establecio una linea de pobreza de 58 ptos de modo tal que aquellos hogares con un score inferior a 58 eran considerados para recibir la intervención y aquellos que superaban este umbral no.
26.2.5 Análisis Parametrico
26.2.5.1 Pasos del análisis
-
Explorar descriptivamente los datos, para
1.1 Examinar si el conjunto de datos permite establecer un quiebre claro en la variable objetivo el cual coincida con el umbral fijado de la variable running.
1.2 Determinar el uso de un modelo de regresión discontinua Sharp o Fuzzy.
1.3 Determinar el uso de una versión lineal o no lineal del modelo de regresión discontinua. 1.4 Analizar el correcto cumplimiento de los supuestos de la metodología de regresión discontinua.
Opcionalmente, se puede preprocesar los datos a analizar, esto es centralizar la variable running.
Estimar el modelo de regresion que incorpora la metodología de regresión discontinua.
Interpretar resultados.
26.2.5.2 Exploración de datos
Sabemos que la intervención empleó la línea de pobreza fijada en 58 como regla para establecer qué hogares recibirían la intervención y cuales no. En primera instancia comprobaremos si la intervención efectivamente fue aplicada en base a esa regla; así como cuan estricta fue su aplicación.
db_treat %>%
ggplot(aes(x = poverty_index, y = enrolled, color = enrolled)) +
geom_point(size = 0.5, alpha = 0.5,
position = position_jitter(width = 0, height = 0.25, seed = 1234)) +
geom_vline(xintercept = 58) + # Establecemos el umbral de intervencion
labs(x = "Indice de pobreza", y = "Participo en la intervencion") +
scale_color_viridis_c("Enrollment:", end = 0.7,option = "A") +
guides(color = FALSE) +
theme_bw()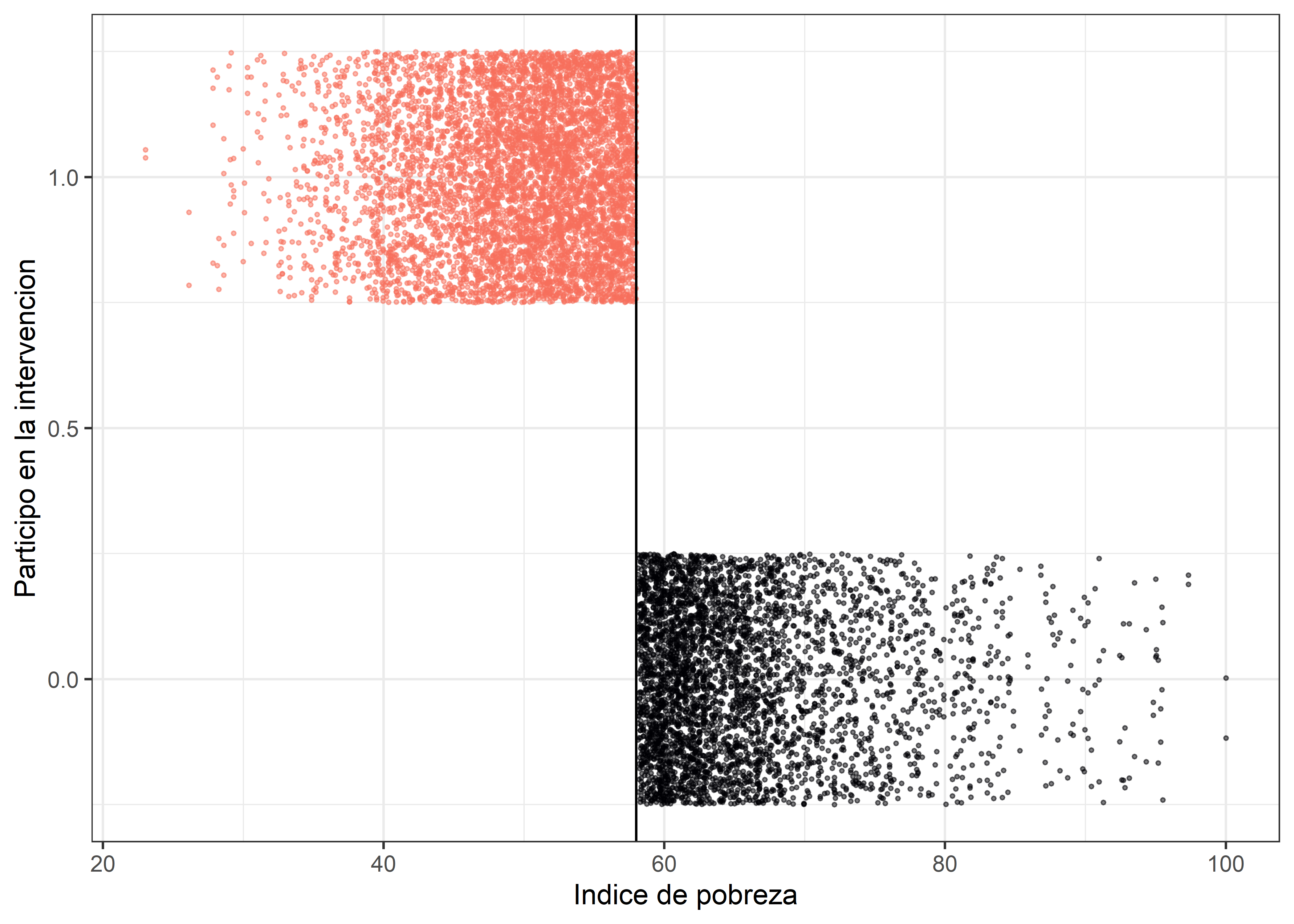
Observamos claramente que ningún hogar con un indice de pobreza superior a 58 participó de la interveción, por lo tanto podemos concluir que la intervención fue diseñada de modo sharp.
Ahora bien, respecto de la variable score, running o indice de eligibilidad, requerimos comprobar si hay un quiebre en el nivel del indice de pobreza establecido, ello lo lograremos al aplicar el test de densidad de McCrary.
test_density <- rdplotdensity(rdd = rddensity(db_treat$poverty_index, c = 58),
X = db_treat$poverty_index, plotGrid = c("es"),
type = "both", histFillCol="gray3")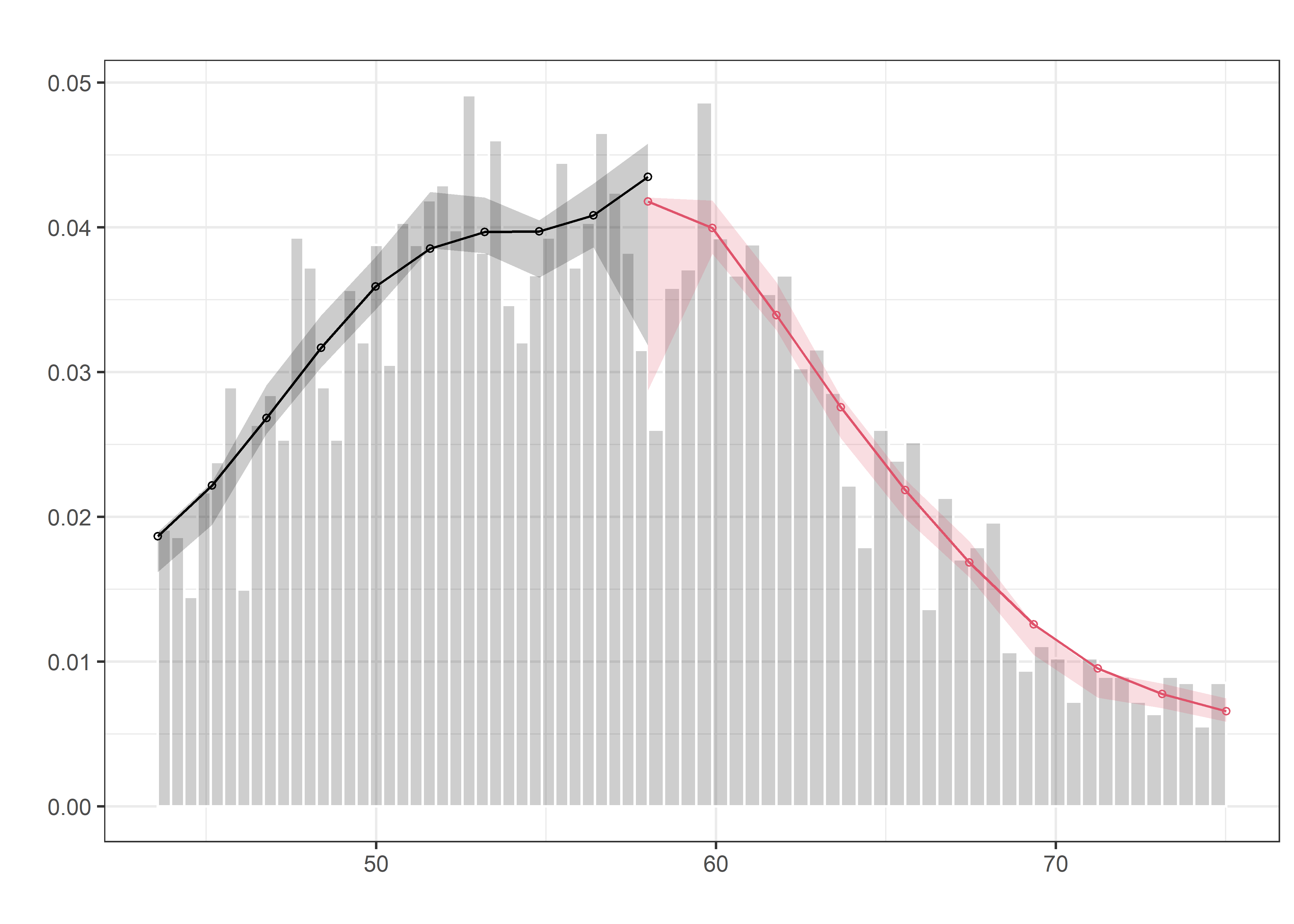
Podemos observar que no hay diferencia significativa en la distribucion del indice de pobreza alrededor del punto de corte, en la medida que los intervalos de confianza de las densidades se superponen.
En último lugar, respecto del análisis descriptivo, podemos comprobar visualmente si efectivamente hay una clara discontinuidad marcada alrededor del punto de corte establecido.
db_treat %>%
filter(round == 1) %>%
mutate(enrolled_lab = ifelse(enrolled == 1, "Tratado", "No Tratado")) %>%
ggplot(aes(x = poverty_index, y = health_expenditures,
group = enrolled_lab, colour = enrolled_lab, fill = enrolled_lab)) +
geom_point(alpha = 0.03) +
geom_smooth(method = "lm") +
labs(x = "Indice de pobreza", y = "Gasto en salud") +
scale_colour_viridis_d("Enrollment:", end = 0.7, option = "A") +
scale_fill_viridis_d("Enrollment:", end = 0.7, option = "A") +
theme_bw() +
theme(legend.position="bottom")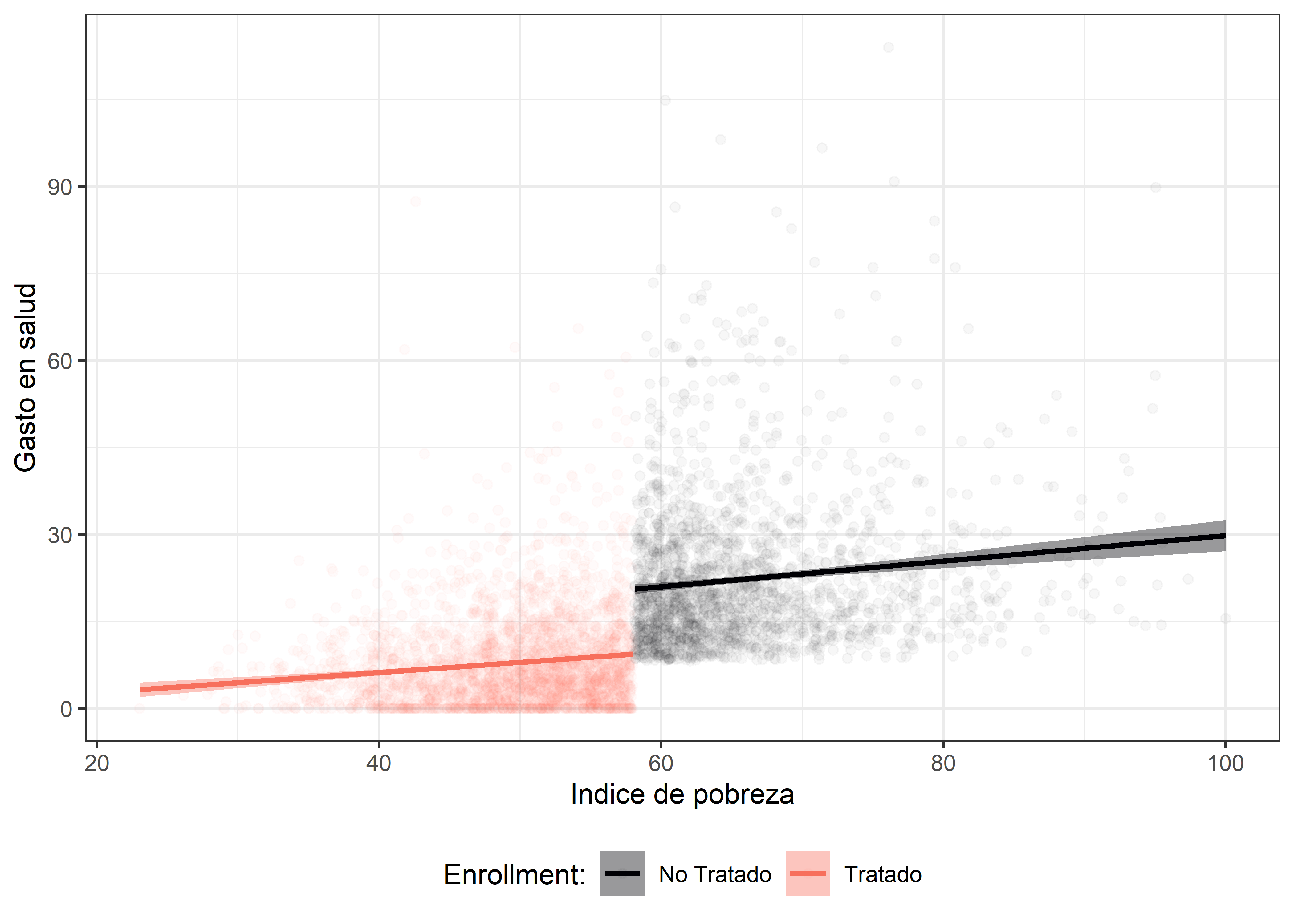
El gráfico anterior muestra la presencia de la interrupción, y por lo tanto dado todo lo anterior queda claro que este conjunto de datos es adecuado para estimar un modelo de regresión discontinua sharp. En ese sentido procedemos a estimar el modelo de regressión discontinua.
26.2.5.3 Ajuste del modelo de regresión
db_treat <- db_treat %>%
mutate(poverty_index_c0 = poverty_index - 58) # Tipicamente se suele centrar en umbral la variable running
library(estimatr)
out_rdd <- lm(health_expenditures ~ poverty_index_c0 * enrolled +
age_hh + age_sp + educ_hh + educ_sp +
female_hh + indigenous + hhsize + dirtfloor +
bathroom + land + hospital_distance,
data = db_treat %>% filter(round == 1)) # Analizaremos aquellos hogares
# una vez ya ejecutado la intervecion(tratamiento)Estimado el modelo, podemos obtener un resumen de los resultados y su estructura final.
summ(out_rdd)| Observations | 4960 |
| Dependent variable | health_expenditures |
| Type | OLS linear regression |
| F(14,4945) | 299.01 |
| R² | 0.46 |
| Adj. R² | 0.46 |
| Est. | S.E. | t val. | p | |
|---|---|---|---|---|
| (Intercept) | 29.22 | 0.92 | 31.76 | 0.00 |
| poverty_index_c0 | 0.17 | 0.03 | 5.71 | 0.00 |
| enrolled | -9.03 | 0.43 | -20.97 | 0.00 |
| age_hh | 0.09 | 0.02 | 5.63 | 0.00 |
| age_sp | -0.05 | 0.02 | -2.99 | 0.00 |
| educ_hh | -0.07 | 0.06 | -1.14 | 0.25 |
| educ_sp | -0.14 | 0.06 | -2.17 | 0.03 |
| female_hh | 0.57 | 0.48 | 1.20 | 0.23 |
| indigenous | -1.88 | 0.29 | -6.45 | 0.00 |
| hhsize | -1.98 | 0.07 | -29.50 | 0.00 |
| dirtfloor | -1.76 | 0.29 | -5.97 | 0.00 |
| bathroom | 0.57 | 0.28 | 2.07 | 0.04 |
| land | -0.05 | 0.04 | -1.11 | 0.27 |
| hospital_distance | -0.01 | 0.00 | -1.73 | 0.08 |
| poverty_index_c0:enrolled | -0.20 | 0.04 | -4.90 | 0.00 |
| Standard errors: OLS |
26.2.5.4 Interpretación de coeficientes principales
El intercepto representa el valor esperado (promedio) del gasto en salud cuando todas las demás variables son cero; es decir, 29.22$ del gasto en salud promedio para aquellos hogares con un índice de pobreza igual a cero y que no superan el umbral.
El coeficiente asociado a la variable running indicaria que el cambio en el gasto en salud asociado con un aumento unitario en el índice de pobreza fue de 0.17 para los hogares que no superan el umbral de 58pts.
el efecto promedio del tratamiento o average treatment effect (ATE) es de -9.03. Ello indica que en promedio el gasto en salud de aquellos individuos por encima de la línea de pobreza es 9 unidades inferior para aquellos que participan de la interveción.
26.3 Series de tiempo interrumpida (ITS)
Las series de tiempo interrumpidas (ITS) son una aplicación específica de RD en la que el umbral es el momento en el que la intervención entró en vigor.
Este puede ser un método particularmente relevante cuando la efectividad de la intervención es repentina, en lugar de gradual, como la finalización de un puente o una conexión importante de transmisión de energía, o la disponibilidad de servicios públicos.
Las series de tiempo interrumpidas se pueden utilizar cuando:
Tenemos datos sobre un resultado a lo largo del tiempo (datos longitudinales)
Queremos entender cómo y si el resultado ha cambiado después de un evento (ej. meteorológico, o, tradicionalmente, una intervención, una política o un programa) al que se expuso toda la población en un momento específico.
Los datos deben incluir observaciones antes y después de que ocurriera el evento. Cuantas más observaciones se tenga a ambos lados del evento, más robusto será el modelo (por lo general).
La variable dependiente en estos modelos por lo general es una medida de resumen de la población (ej. promedios o conteos). Por ejemplo, el producto bruto interno de un país, la tasa de criminalidad en una ciudad, el puntaje promedio de matemáticas en una escuela, o los casos de malaria en una cuidad.
A diferencia de la mayoría de los otros modelos que requieren muchos controles, estos modelos son flexibles porque pueden generar inferencias válidas en ciertas circunstancias con solo dos variables independientes: el tiempo y la fecha de inicio del evento.
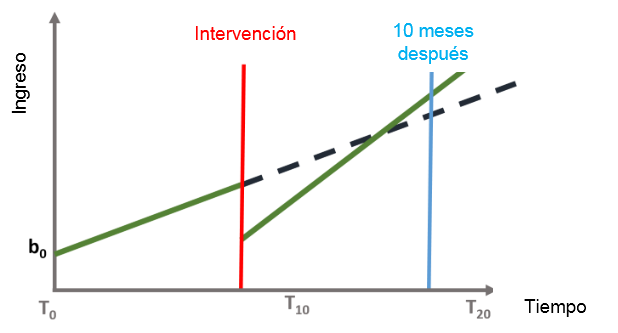
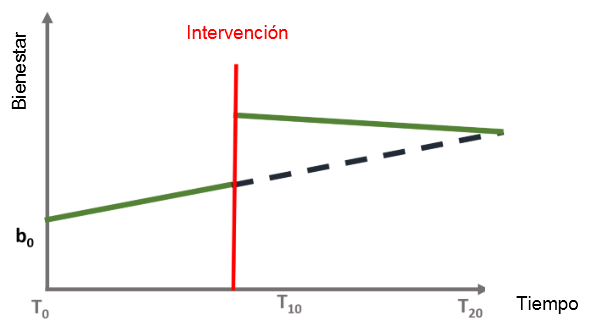
Las series de tiempo interrumpidas nos permiten investigar cada efecto, entendiendo así si el evento:
No tiene ningún efecto (A)
Tiene solo un efecto inmediato (B)
Tiene un efecto sostenido a largo plazo (C)
Tiene un efecto inmediato y sostenido (D)
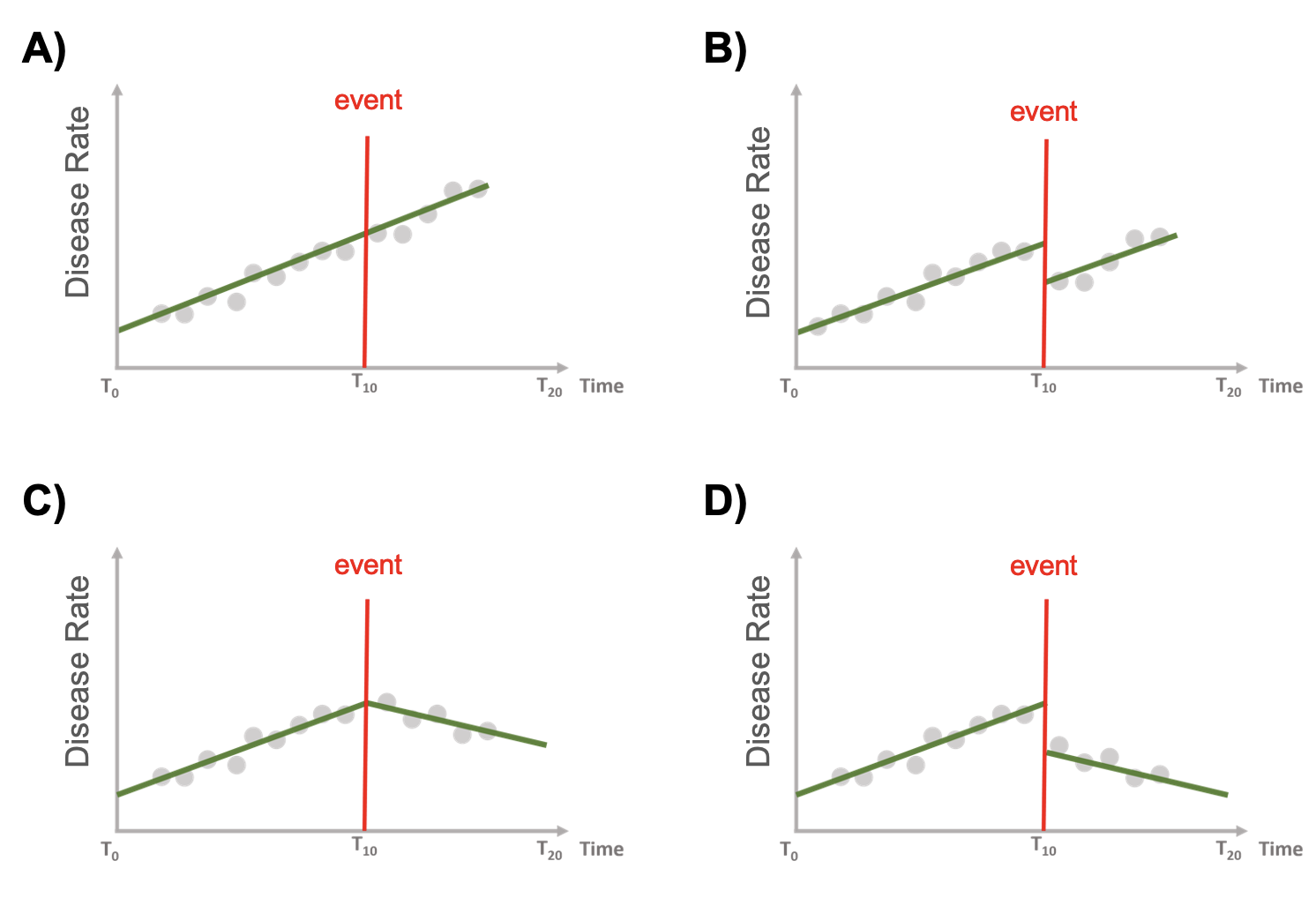
26.3.1 Modelo ITS
Donde :
Variables:
Coeficientes:
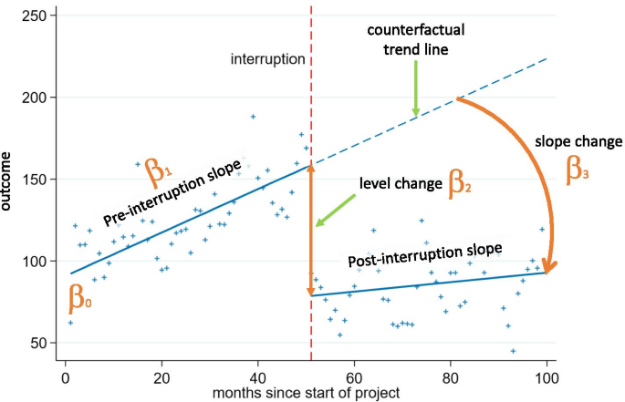
Créditos: Turner, 2021
26.3.2 Supuestos del modelo ITS
Shock bien definido
No hay eventos simultáneos
Tendencia previa al evento bien establecida (tamaño muestra de análisis considerable)
Correcta especificación del modelo
La tendencia previa al evento se hubiera mantenido en ausencia del evento.
26.3.3 Caso de estudio
Impacto en Salud: Muertes semanales por dengue en Iquitos (por 10,000 habitantes)
-
Evento: Evento de lluvias extremo (PDSI > 4 ~
01-11-2015)Índice de severidad de la sequía de Palmer (PDSI): El PDSI se calcula utilizando los niveles de humedad del suelo, la tasa de evapotranspiración esperada (es decir, la cantidad de evaporación del suelo que ocurriría si hubiera suficientes niveles de agua disponibles, según la temperatura media diaria y la duración de los días del mes) y la precipitación.
El índice varía de −10 (muy seco) a 10 (muy húmedo), con valores por debajo de −4 o por encima de 4 clasificados como extremos.
26.3.4 Análisis paramétrico
26.3.4.1 Pasos del análisis
Explorar de forma gráfica los datos y confirmar si ITS es un diseño adecuado para la pregunta de investigación.
Poner en formato la base de datos. Crear las variables T (tiempo desde el inicio del estudio), D (indicador pre/post evento desde el
01-11-2015), P (tiempo desde el inicio del evento)Realizar el modelo de regresión segmentada para ITS usando las tres variables creadas.
Interpretar resultados de los coeficientes.
Calcular los valores predichos en base al modelo ITS.
Graficar los resultados del ITS junto con los valores del paso 1.
Calcular el escenario contrafactual (sin evento) y graficarlo.
26.3.4.2 Exploración de datos
dat %>%
ggplot(aes(x = date, y = dengue_cases)) +
geom_point(alpha = .6) +
geom_vline(aes(xintercept = dmy("01-11-2015")),
linetype = "dashed", col = "red3") +
theme_bw()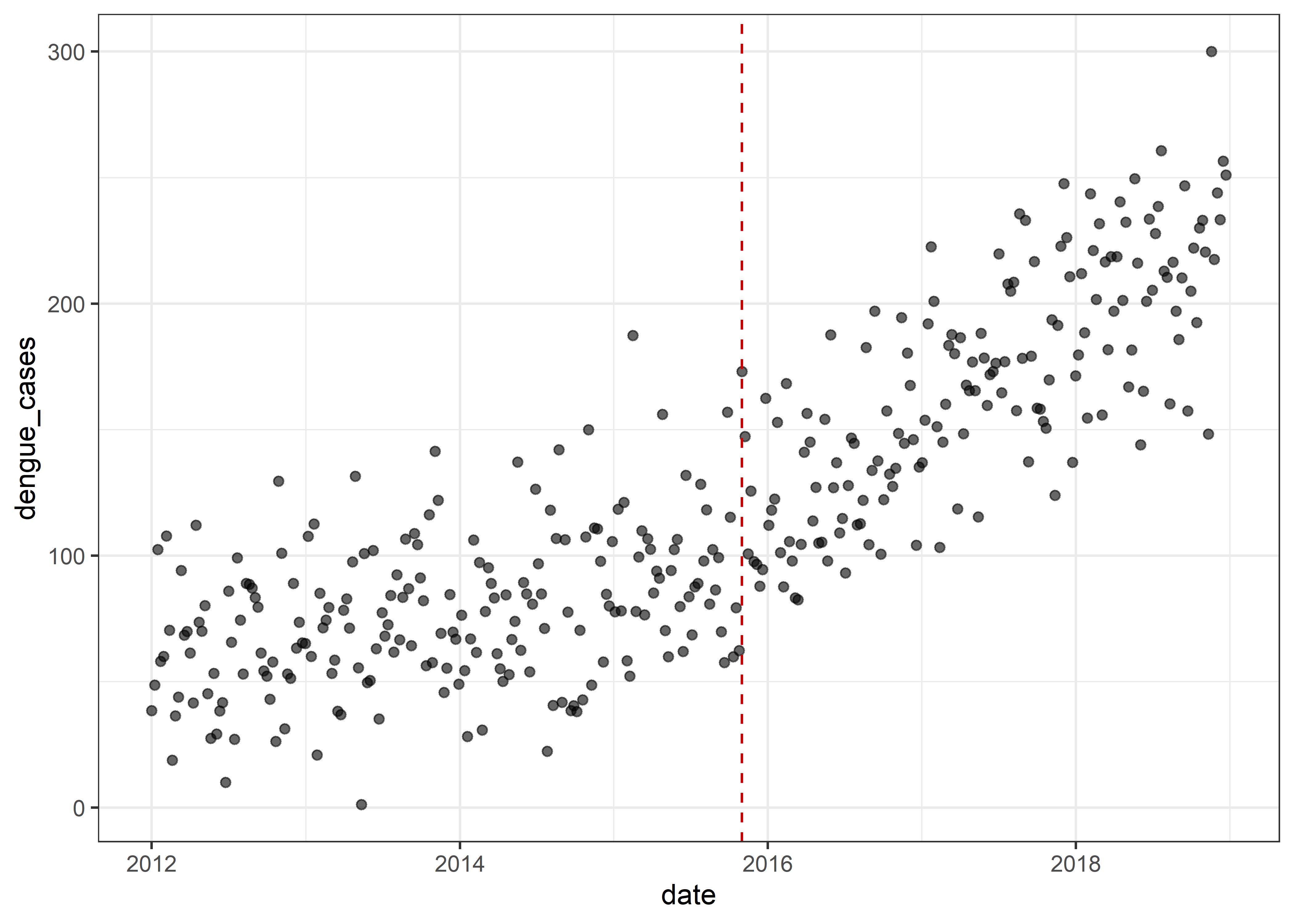
26.3.4.3 Formato de datos
-
Crear las variables:
| dengue_cases | date | T | D | P |
|---|---|---|---|---|
| 38.50479 | 2012-01-01 | 1 | 0 | 0 |
| 48.61841 | 2012-01-08 | 2 | 0 | 0 |
| 102.44811 | 2012-01-15 | 3 | 0 | 0 |
| 58.05859 | 2012-01-22 | 4 | 0 | 0 |
| 60.03438 | 2012-01-29 | 5 | 0 | 0 |
| 107.77661 | 2012-02-05 | 6 | 0 | 0 |
| 70.40195 | 2012-02-12 | 7 | 0 | 0 |
| 18.88587 | 2012-02-19 | 8 | 0 | 0 |
| 36.42974 | 2012-02-26 | 9 | 0 | 0 |
| 43.87267 | 2012-03-04 | 10 | 0 | 0 |
| 94.13151 | 2012-03-11 | 11 | 0 | 0 |
| 68.44217 | 2012-03-18 | 12 | 0 | 0 |
| 69.88381 | 2012-03-25 | 13 | 0 | 0 |
| 61.40350 | 2012-04-01 | 14 | 0 | 0 |
| 41.64085 | 2012-04-08 | 15 | 0 | 0 |
| 112.07083 | 2012-04-15 | 16 | 0 | 0 |
| 73.64975 | 2012-04-22 | 17 | 0 | 0 |
| 70.00000 | 2012-04-29 | 18 | 0 | 0 |
| 80.17728 | 2012-05-06 | 19 | 0 | 0 |
| 45.20039 | 2012-05-13 | 20 | 0 | 0 |
26.3.4.4 Modelo de regresión
| Observations | 365 |
| Dependent variable | dengue_cases |
| Type | OLS linear regression |
| F(3,361) | 398.71 |
| R² | 0.77 |
| Adj. R² | 0.77 |
| Est. | S.E. | t val. | p | |
|---|---|---|---|---|
| (Intercept) | 58.37 | 4.10 | 14.23 | 0.00 |
| T | 0.18 | 0.04 | 5.15 | 0.00 |
| D | 13.60 | 6.08 | 2.24 | 0.03 |
| P | 0.55 | 0.06 | 9.34 | 0.00 |
| Standard errors: OLS |
26.3.4.5 Interpretación de coeficientes
El coeficiente de tiempo (
T) indica la tendencia de las muertes por dengue antes del evento. Es positivo y significativo, lo que indica que las muertes por dengue en la población de Iquitos aumenta con el tiempo. Por cada semana que pasa, las muertes aumentan en 0.18 por cada 10,000 habitantes.El coeficiente del evento (
D) indica el aumento de las muertes por dengue inmediatamente después del evento. Podemos ver que el efecto inmediato es positivo y significativo indicando que el inicio de lluvias extremas aumentó las muertes por dengue en la población de Iquitos en 13.6 por cada 10,000 habitantes.El coeficiente de tiempo transcurrido desde el evento (
P) indica que la tendencia ha cambiado después del evento. El efecto sostenido es positivo y significativo, lo que indica que por cada semana las muertes diarias por dengue han aumentado en 0.55 por cada 10,000 habitantes con respecto a la tendencia pre-evento.
26.3.4.6 Predicción de valores del modelo
pred <- augment(fit, interval = "confidence")| dengue_cases | T | D | P | .fitted | .lower | .upper | .resid | .hat | .sigma | .cooksd | .std.resid |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 38.50479 | 1 | 0 | 0 | 58.55599 | 50.54917 | 66.56280 | -20.0511934 | 0.0198507 | 28.91821 | 0.0024870 | -0.7008569 |
| 48.61841 | 2 | 0 | 0 | 58.73831 | 50.79162 | 66.68500 | -10.1199008 | 0.0195537 | 28.93289 | 0.0006237 | -0.3536711 |
| 102.44811 | 3 | 0 | 0 | 58.92064 | 51.03392 | 66.80736 | 43.5274741 | 0.0192597 | 28.84504 | 0.0113574 | 1.5209738 |
| 58.05859 | 4 | 0 | 0 | 59.10296 | 51.27605 | 66.92988 | -1.0443765 | 0.0189687 | 28.93785 | 0.0000064 | -0.0364881 |
| 60.03438 | 5 | 0 | 0 | 59.28529 | 51.51803 | 67.05255 | 0.7490859 | 0.0186807 | 28.93788 | 0.0000033 | 0.0261675 |
| 107.77661 | 6 | 0 | 0 | 59.46762 | 51.75983 | 67.17540 | 48.3089896 | 0.0183957 | 28.82357 | 0.0133386 | 1.6873104 |
| 70.40195 | 7 | 0 | 0 | 59.64994 | 52.00147 | 67.29842 | 10.7520064 | 0.0181137 | 28.93225 | 0.0006502 | 0.3754864 |
| 18.88587 | 8 | 0 | 0 | 59.83227 | 52.24293 | 67.42161 | -40.9463967 | 0.0178347 | 28.85586 | 0.0092798 | -1.4297452 |
| 36.42974 | 9 | 0 | 0 | 60.01459 | 52.48421 | 67.54498 | -23.5848589 | 0.0175587 | 28.91072 | 0.0030294 | -0.8234083 |
| 43.87267 | 10 | 0 | 0 | 60.19692 | 52.72530 | 67.66854 | -16.3242463 | 0.0172857 | 28.92489 | 0.0014279 | -0.5698424 |
| 94.13151 | 11 | 0 | 0 | 60.37925 | 52.96621 | 67.79228 | 33.7522612 | 0.0170157 | 28.88223 | 0.0060058 | 1.1780530 |
| 68.44217 | 12 | 0 | 0 | 60.56157 | 53.20693 | 67.91621 | 7.8805967 | 0.0167487 | 28.93487 | 0.0003221 | 0.2750186 |
| 69.88381 | 13 | 0 | 0 | 60.74390 | 53.44745 | 68.04034 | 9.1399151 | 0.0164847 | 28.93383 | 0.0004262 | 0.3189237 |
| 61.40350 | 14 | 0 | 0 | 60.92622 | 53.68777 | 68.16468 | 0.4772725 | 0.0162237 | 28.93789 | 0.0000011 | 0.0166515 |
| 41.64085 | 15 | 0 | 0 | 61.10855 | 53.92789 | 68.28921 | -19.4677010 | 0.0159656 | 28.91941 | 0.0018707 | -0.6791173 |
| 112.07083 | 16 | 0 | 0 | 61.29088 | 54.16779 | 68.41396 | 50.7799512 | 0.0157106 | 28.81189 | 0.0125182 | 1.7711941 |
| 73.64975 | 17 | 0 | 0 | 61.47320 | 54.40747 | 68.53893 | 12.1765462 | 0.0154586 | 28.93068 | 0.0007079 | 0.4246610 |
| 70.00000 | 18 | 0 | 0 | 61.65553 | 54.64694 | 68.66412 | 8.3444727 | 0.0152096 | 28.93451 | 0.0003269 | 0.2909794 |
| 80.17728 | 19 | 0 | 0 | 61.83785 | 54.88617 | 68.78953 | 18.3394248 | 0.0149636 | 28.92151 | 0.0015528 | 0.6394327 |
| 45.20039 | 20 | 0 | 0 | 62.02018 | 55.12518 | 68.91518 | -16.8197930 | 0.0147206 | 28.92412 | 0.0012843 | -0.5863760 |
26.3.4.7 Gráfico del modelo ITS
dat_its %>%
ggplot(aes(x = T, y = dengue_cases)) +
geom_point(alpha = .6) +
geom_vline(aes(xintercept = 200), linetype = "dashed", col = "red3") +
geom_line(data = pred, aes(y = .fitted), col = "deepskyblue3") +
geom_ribbon(data = pred, aes(ymin = .lower, ymax = .upper),
fill = "deepskyblue3", alpha = .3) +
theme_bw()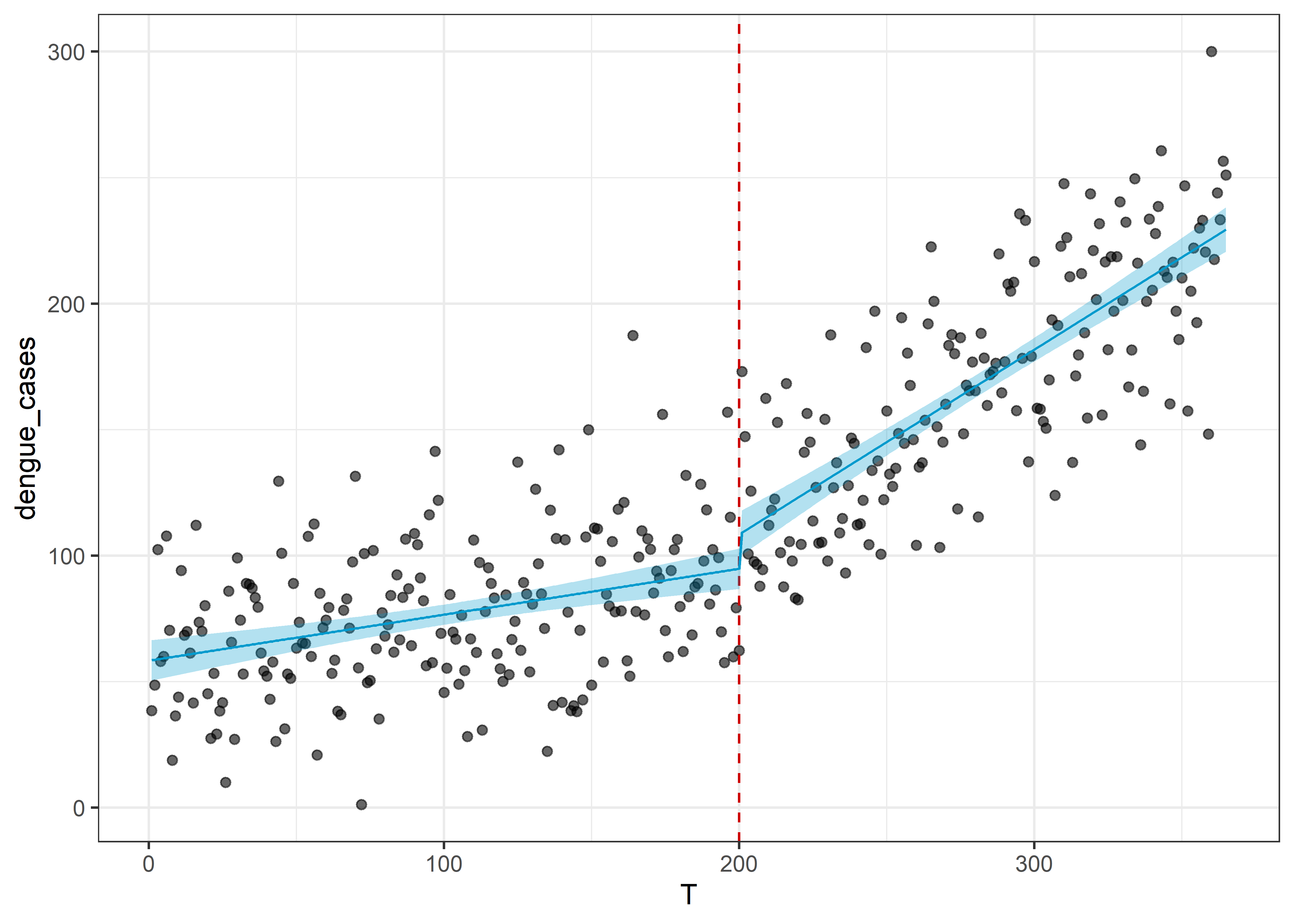
26.3.4.8 Escenario Contrafactual
conterfactual <- dat_its %>%
mutate(D = 0,
P = 0) %>%
augment(fit, newdata = ., interval = "confidence")
dat_its %>%
ggplot(aes(x = T, y = dengue_cases)) +
geom_point(alpha = .6) +
geom_vline(aes(xintercept = 200), linetype = "dashed", col = "red3") +
geom_line(data = pred, aes(y = .fitted), col = "deepskyblue3") +
geom_ribbon(data = pred, aes(ymin = .lower, ymax = .upper), fill = "deepskyblue3", alpha = .3) +
geom_line(data = conterfactual, aes(y = .fitted), col = "orange2", linetype = "dashed") +
geom_ribbon(data = conterfactual, aes(ymin = .lower, ymax = .upper),
fill = "orange2", alpha = .3) +
theme_bw()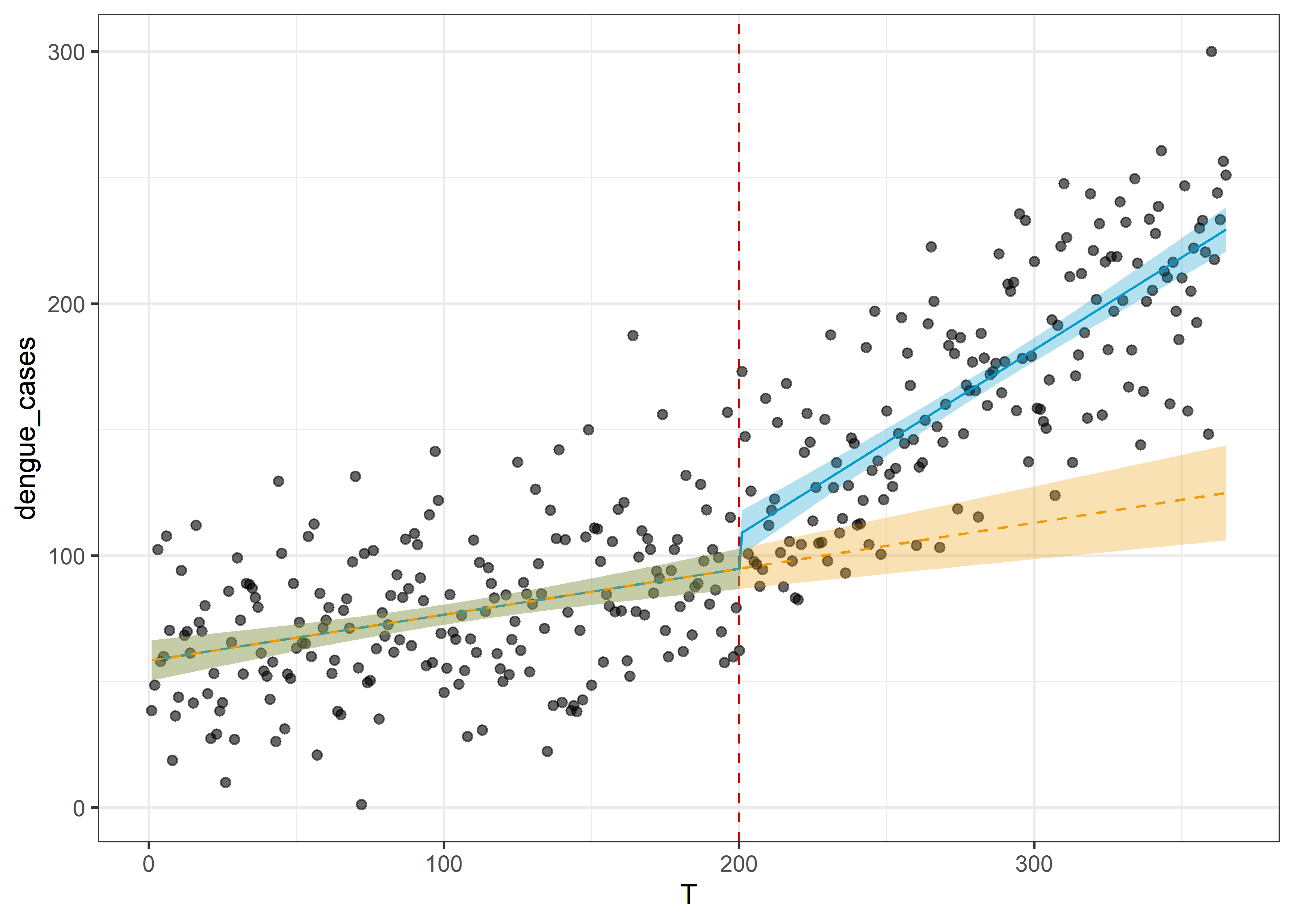
26.3.5 Consideraciones finales
Algunas consideraciones que se deben tomar en cuenta al interpretar estos modelos son:
Efectos rezagados
Regresión a la media
Autocorrelación
Finalmente, las series de tiempo también están sujetas a amenazas a la validez interna, tales como:
Otro hecho ocurrió al mismo tiempo del evento de interés y provocó el efecto inmediato y sostenido que observamos;
Procesos de selección (vulnerabilidad), ya que las personas se ven afectadas de diferente manera por el evento.
Para abordar estos problemas puede :
- Utilizar como control un grupo que no esté expuesto al evento (por ejemplo, una población con características comparables donde no hubo eventos de lluvias extremas)
26.4 Diferencia en diferencias (dif-in-dif)
26.4.1 Descripcion general del diseño
En varias ocasiones (en evaluaciones de determinadas intervenciones) no se tiene certeza de la regla de asignación entre los grupos de tratamiento y control. Así, por ejemplo, entre los distritos miembros de una provincia se puede estar aplicando una intervención contra la anemia, ante la cual los distritos pueden participar voluntariamente (Gertler et al. 2017). Este tipo de interveción origina al momento de su evaluación 2 problemas:
El solo observar un indicador como la concentración de hemoglobina en la sangre, antes y despues de la intervecion en aquellos distritos que se inscribieron en el programa no capturara el impacto causal de la interveción, puesto que puede haber muchos otros factores afectando la anemia a la par.
El solo comparar la intervención entre aquellos que la recibieron y aquellos que no también es problemático dado que no se tiene certeza de que no hayan otros factores no observables por los que determinados distritos no se incribieron a la intervencion y otros si (Sesgo de seleccion).
En ese tipo de situaciones se puede considerar emplear el método de Diferencia en Diferencias. Diferencia en diferencias es una metodología para evaluar el efecto de una interveción que contrasta las diferencias a lo largo del tiempo entre una población beneficiaria de la intervecion (grupo de tratamiento) y otra que no (grupo de comparación). Asi esta metodología en general en su desarrollo lleva a cabo:
La diferencia en los resultados antes y despues del grupo de tratamiento (primera diferencia).
La diferencia en los resultados antes y despues del grupo no tratado pero expuesto a las mismas condiciones que el grupo de tratamiento salvo la intervención ( Segunda diferencia).
26.4.2 Modelo
Variables:
donde:
Variables
Parámetros
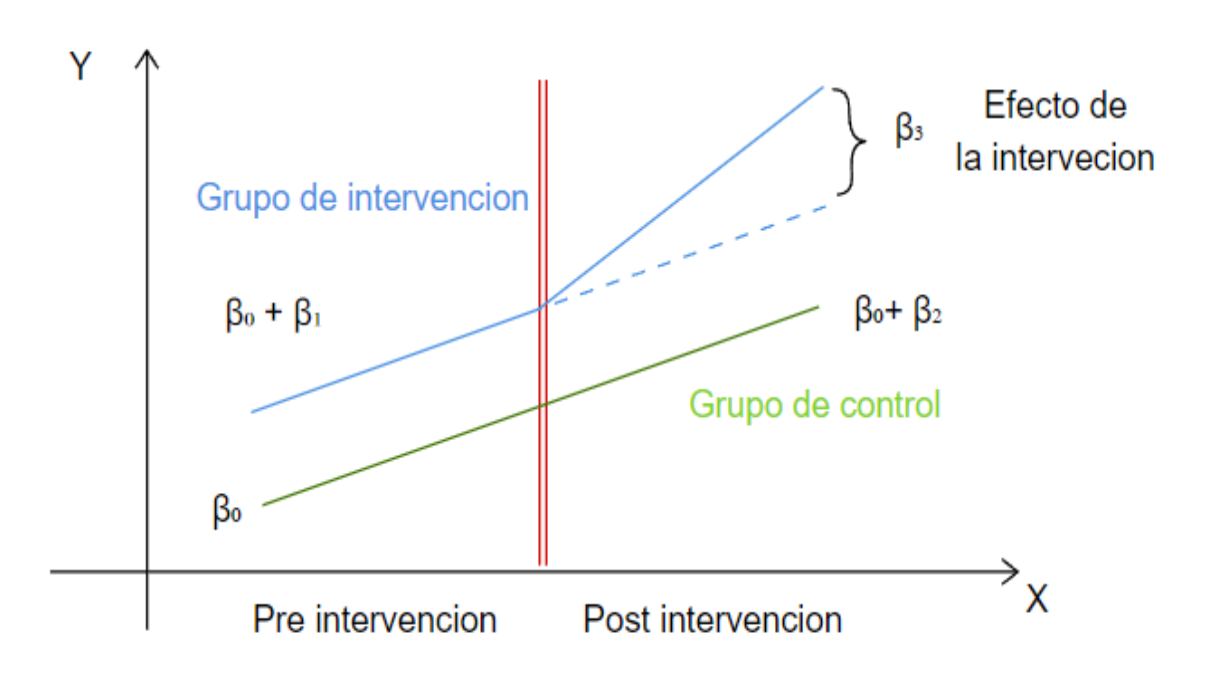
26.4.3 Supuestos
Tendencias paralela: Este supuesto afirma que en ausencia de intervención, los grupos de tratamiento y control tendrían tendencias comunes en el atributo bajo analisis. Este supuesto es clave por que asegura que la estimación del efecto del tratamiento sea insesgada.
La composición de aquellas unidades de análisis que conforman los grupos de tratamiento y control como por ejemplo individuos, hogares, familias, etc, no cambian con el paso del tiempo.
Supuestos usuales de un modelo de regresión (Homocedasticidad, no autocorrelacion,etc)
26.4.4 Caso de Estudio
Emplearemos los mismos datos del programa social investigado en la sección de RD, el cual consistio en un subsidio económico para solventar parte del gasto en salud de un grupo de hogares.
| health_expenditures | poverty_index | enrolled | round | locality_identifier | age_hh | age_sp | educ_hh | educ_sp | female_hh | indigenous | hhsize | dirtfloor | bathroom | land | hospital_distance | poverty_index_c0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 15.1854553 | 55.95054 | 1 | 0 | 26 | 24 | 23 | 0 | 6 | 0 | 0 | 4 | 1 | 0 | 1 | 124.82 | -2.0494576 |
| 19.5809021 | 55.95054 | 1 | 1 | 26 | 25 | 24 | 0 | 6 | 0 | 0 | 4 | 1 | 0 | 1 | 124.82 | -2.0494576 |
| 13.0762568 | 46.05873 | 1 | 0 | 26 | 30 | 26 | 4 | 0 | 0 | 0 | 6 | 1 | 0 | 2 | 124.82 | -11.9412689 |
| 2.3988545 | 46.05873 | 1 | 1 | 26 | 31 | 27 | 4 | 0 | 0 | 0 | 6 | 1 | 0 | 2 | 124.82 | -11.9412689 |
| 0.0000000 | 54.09583 | 1 | 1 | 26 | 59 | 57 | 0 | 0 | 0 | 0 | 6 | 1 | 0 | 4 | 124.82 | -3.9041748 |
| 15.2863531 | 54.09583 | 1 | 0 | 26 | 58 | 56 | 0 | 0 | 0 | 0 | 6 | 1 | 0 | 4 | 124.82 | -3.9041748 |
| 20.0269089 | 56.90340 | 1 | 1 | 26 | 36 | 25 | 3 | 0 | 0 | 0 | 7 | 1 | 0 | 2 | 124.82 | -1.0965996 |
| 11.3117609 | 56.90340 | 1 | 0 | 26 | 35 | 24 | 3 | 0 | 0 | 0 | 7 | 1 | 0 | 2 | 124.82 | -1.0965996 |
| 11.2239122 | 46.90881 | 1 | 0 | 26 | 37 | 35 | 0 | 0 | 0 | 0 | 7 | 1 | 0 | 2 | 124.82 | -11.0911903 |
| 16.6646862 | 46.90881 | 1 | 1 | 26 | 39 | 36 | 0 | 0 | 0 | 0 | 7 | 1 | 0 | 2 | 124.82 | -11.0911903 |
| 8.8769245 | 48.18393 | 1 | 0 | 26 | 34 | 41 | 0 | 2 | 1 | 0 | 9 | 1 | 0 | 1 | 124.82 | -9.8160744 |
| 0.1155464 | 48.18393 | 1 | 1 | 26 | 35 | 41 | 0 | 2 | 1 | 0 | 9 | 1 | 0 | 1 | 124.82 | -9.8160744 |
| 0.0000000 | 49.69088 | 1 | 1 | 26 | 31 | 30 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 1 | 124.82 | -8.3091202 |
| 12.6858168 | 49.69088 | 1 | 0 | 26 | 30 | 29 | 0 | 6 | 0 | 0 | 7 | 0 | 0 | 1 | 124.82 | -8.3091202 |
| 17.2236977 | 57.10974 | 1 | 1 | 26 | 58 | 57 | 3 | 0 | 0 | 0 | 9 | 0 | 0 | 4 | 124.82 | -0.8902626 |
| 12.6680889 | 57.10974 | 1 | 0 | 26 | 57 | 56 | 3 | 0 | 0 | 0 | 9 | 0 | 0 | 4 | 124.82 | -0.8902626 |
| 10.5806131 | 49.69088 | 1 | 0 | 26 | 24 | 28 | 2 | 6 | 0 | 0 | 7 | 1 | 0 | 2 | 124.82 | -8.3091202 |
| 1.2849009 | 49.69088 | 1 | 1 | 26 | 25 | 29 | 2 | 6 | 0 | 0 | 7 | 1 | 0 | 2 | 124.82 | -8.3091202 |
| 7.2307086 | 52.62751 | 1 | 0 | 26 | 40 | 36 | 0 | 2 | 0 | 0 | 9 | 1 | 0 | 1 | 124.82 | -5.3724899 |
| 6.4174824 | 52.62751 | 1 | 1 | 26 | 40 | 37 | 0 | 2 | 0 | 0 | 9 | 1 | 0 | 1 | 124.82 | -5.3724899 |
Los paquete que usaremos son:
26.4.5 Análisis Parametrico
26.4.5.1 Pasos del análisis
- Explorar descriptivamente los datos, para detectar anomalías tales como outliers.
- Estimar el modelo de regresión que incorpora la metodología de regresión de diferencia en diferencias.
- Resumir la información de los resultados y proceder a interpretarlos.
26.4.5.2 Exploración de datos
En primera instancia, realizaremos una exploración de los datos. Para ello observamos la distribución de la variable objetivo para así detectar potenciales problemas que puedan dificultar la estimación de un modelo de regresión lineal simple.
db_treat %>%
ggplot(aes(x = health_expenditures)) +
geom_histogram(binwidth = 8, color = "white", boundary = 0) +
labs(x = "Gasto en Salud",
y = "Frecuencia") +
facet_wrap(~ enrolled) +
theme_bw()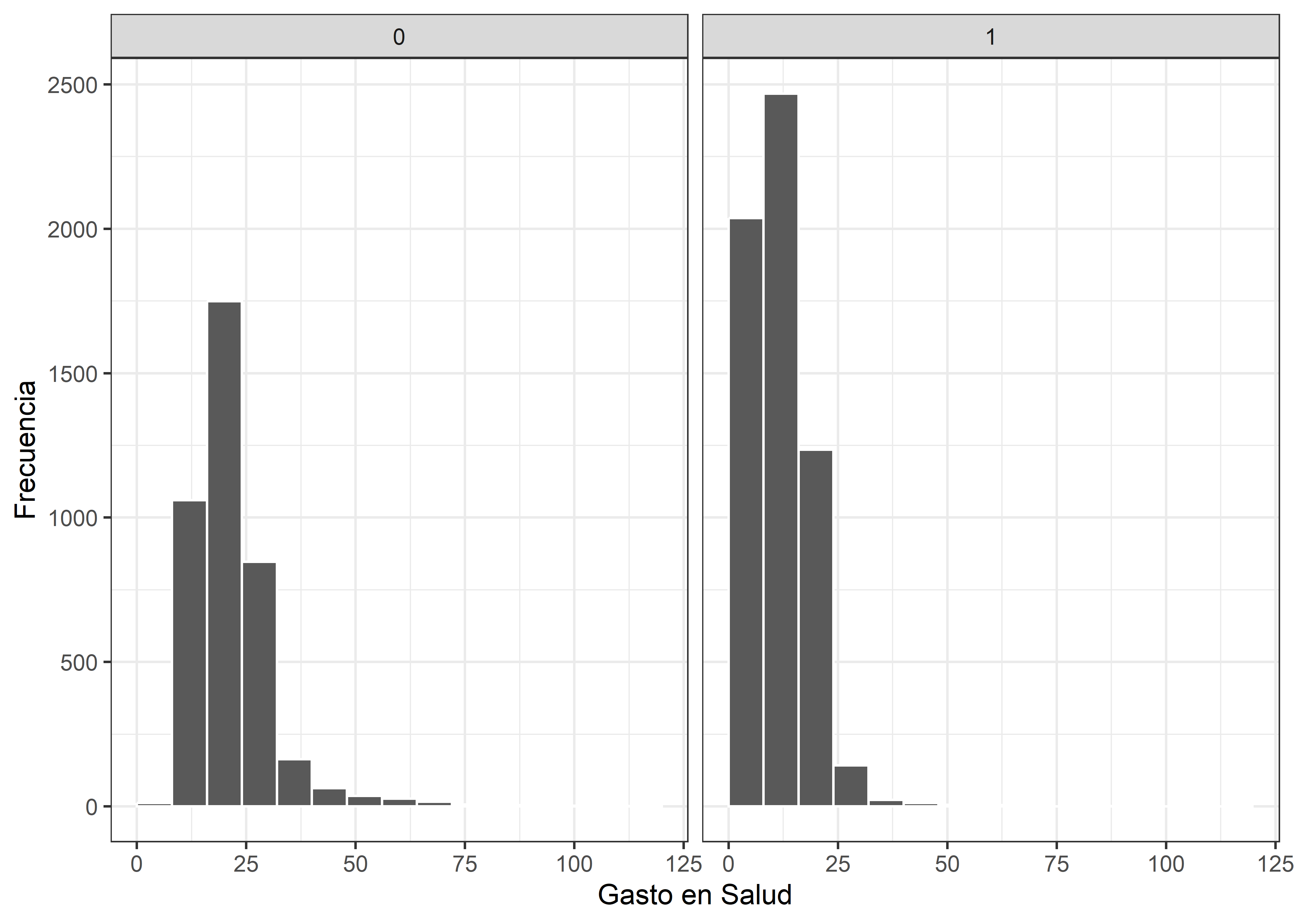
Se observa que las distribuciones son sesgadas, por lo que opcionalmente se podría continuar el análisis con el logaritmo del gasto en salud para facilitar el cumplimiento de los supuestos del modelo de regresión lineal simple.
26.4.5.3 Ajuste del modelo de regresion
Dado que no se detecto alguna anomalía adicional, ejecutamos el ajuste del modelo de regresión planteado.
out_did <- lm(health_expenditures ~ round * enrolled,
data = db_treat)y finalmente procedemos a revisar el resumen de los resultados obtenidos.
summ(out_did)| Observations | 9919 |
| Dependent variable | health_expenditures |
| Type | OLS linear regression |
| F(3,9915) | 1730.14 |
| R² | 0.34 |
| Adj. R² | 0.34 |
| Est. | S.E. | t val. | p | |
|---|---|---|---|---|
| (Intercept) | 20.79 | 0.18 | 117.36 | 0.00 |
| round | 1.51 | 0.25 | 6.04 | 0.00 |
| enrolled | -6.30 | 0.23 | -27.50 | 0.00 |
| round:enrolled | -8.16 | 0.32 | -25.19 | 0.00 |
| Standard errors: OLS |
Como se observa, el modelo ajustado final es:
26.4.5.4 Interpretación de coeficientes principales
El intercepto muestra que 20.79 fue el valor esperado (promedio) del gasto en salud de un hogar que forma parte del grupo de hogares que no recibieron la intervencion
El segundo parámetro, indica que en el periodo previo a la subvención económica
El tercer parámetro muestra que el gasto en salud promedio para aquellos hogares que no recibieron el tratamiento
El cuarto parámetro indica que producto de la intervencion,en promedio, el gasto en salud se ha reducido en -8.16$ (Average Treatment Effect) para el grupo de tratamiento, esto es aquellos que recibieron la subvención económica.