21 Estudios de supervivencia
21.1 Paquetes y data
En esta sección utilizaremos los comandos de tidyverse de la plataforma R para la visualización de datos. Los paquetes y bases de datos a ser utilizados en esta sección son:
Utilizaremos la base de datos cancer del North Central Cancer Treatment Group, la cual contiene los datos de un estudio de supervivencia de pacientes con cáncer de pulmón avanzado. El objetivo del estudio fue determinar si la auto evaluación de los pacientes podría brindar información de pronóstico complementaria a la evaluación del médico. El conjunto de datos registra un total de 228 pacientes, de los cuales 63 abandonaron el estudio.
A continuación se adjunta su diccionario.
| Variable | Nombre |
|---|---|
| Código de institución | inst |
| Tiempo de supervivencia en días | time |
| Estado de la censura, 1 = censurado, 2 = muerto | status |
| Edad en años | age |
| Sexo, 1 = Masculino, 2 = Femenino | sex |
| Puntuación ECOG según la valoración del médico. 0= asintomático, 1= sintomático pero completamente ambulatorio, 2= en cama <50% del día, 3= en cama > 50% del día pero no encamado, 4 = encamado | ph.ecog |
| Puntuación de Karnofsky (malo=0, bueno=100) valorada por el médico | ph.karno |
| Puntuación de Karnofsky según la valoración del paciente | pat.karno |
| Calorías consumidas en las comidas | meal.cal |
| Pérdida de peso en los últimos seis meses en libras | wt.loss |
21.2 Introducción
El análisis de supervivencia es un conjunto de métodos cuya variable de interés es el tiempo hasta la ocurrencia de un evento. Entre los estudios que evalúan la supervivencia a un evento están los ensayos clínicos, los estudios longitudinales y los estudios experimentales. Ejemplos de variables tiempo a evento podrían ser el seguimiento de ingreso hospitalario hasta la muerte o el tiempo desde el inicio de quimioterapia hasta la remisión cáncer de mama.
Una característica de este análisis es que terminado el periodo de seguimiento, el evento no será observado en todos los participantes de estudio. Además, es posible presentar pérdida de participantes o retiro de participantes del estudio. Podemos englobar todos estos casos en el término de censura, el cuál puede clasificarse en tres tipos:
Censura tipo I o administrativa, se da cuando el tiempo de seguimiento esta pre-definido y no se observa el evento hasta el término del estudio. Por ejemplo, si se desea evaluar la incidencia de cáncer de pulmón en fumadores durante 4 años de seguimiento. Los individuos que no hayan desarrollado cáncer de pulmón durante esos 4 años, son censurados.
Censura tipo II, se observa cuando los individuos son seguidos hasta que ocurra un número o porcentaje determinado del evento de interés. Por ejemplo, un estudio desea evaluar un nuevo dispositivo biomédico, y se define el término del estudio (censura de los participantes) si es que el 30% de los dispositivos fallan.
Censura tipo III o aleatorio, son pérdidas de seguimiento o muerte por otra causa no relacionada al evento de interés, los cuales no se relacionan con el evento de interés. Una manera de garantizar la aleatoriedad de estas censuras es determinar si la causa de esta podría conducir a un sesgo en la estimación de la supervivencia.
En el siguiente gráfico de seguimiento, se presenta un registro del progreso a muerte realizado a pacientes diagnosticados con cáncer de colon.
col <- colon %>%
filter(id < 21) %>%
mutate(id = factor(id)) %>%
mutate(time_months = time/30) %>%
group_by(id) %>%
mutate(last_month_followup = max(time_months),
month_death = case_when(status == 1 ~ last_month_followup,
TRUE ~ NA_real_)) %>%
ungroup(id) %>%
mutate(sex = factor(sex))
col_2 <- col %>%
group_by(id) %>%
slice_head(n=1) %>%
mutate(time_months=0)
col %>%
bind_rows(col_2)%>%
ggplot(aes(x = time_months, y = id, group = id, col= sex)) +
geom_line() +
geom_point(shape = 15) +
geom_point(aes(x = month_death, y = id), col = "black", shape = 4)+
labs(x = "Tiempo de seguimiento (meses)", y = "Patient ID", col = "Sexo",
title = "Seguimiento de Ensayo clínco",
subtitle = "x indica el mes de fallecimiento del paciente")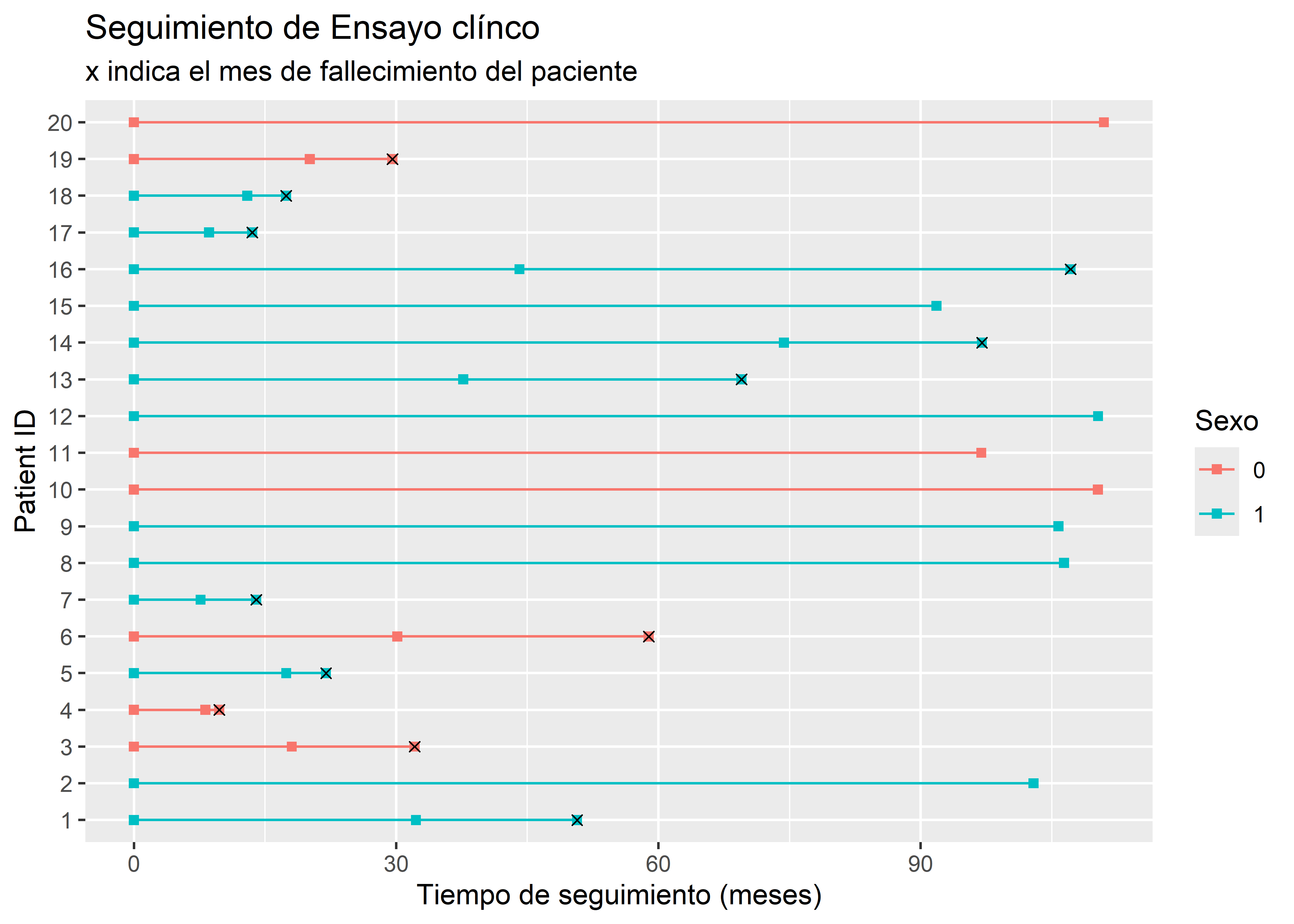
En la figura presentada, se muestra el seguimiento de 20 participantes en el estudio. De estos, 12 fallecieron durante el período de estudio. Además, se puede observar que el participante número 15 se retiró poco después de los 90 meses sin experimentar el evento de interés, lo que posiblemente se considera una pérdida de seguimiento. También es relevante destacar que los participantes 10, 12 y 20 no experimentaron el evento al final del período de seguimiento. La variabilidad en las contribuciones de tiempo por parte de cada persona durante el estudio resalta la necesidad de emplear nuevas herramientas para el análisis de la variable de tiempo hasta el evento.
21.3 Funciones para el análisis de supervivencia
El análisis de supervivencia tuvo sus inicios enfocados en temas de medicina y la salud pública en el siglo XX. Su principal aplicación estuvo centrada en la construcción de tablas de mortalidad y tasas de mortalidad por edad. Más tarde, surgió la necesidad de métodos robustos que consideraran las censuras, lo que llevó al desarrollo del estimado Kaplan-Meier en la década de 1950. Este método permitió calcular la función de supervivencia, S(t), aplicándose ampliamente en estudios clínicos y epidemiológicos. Poco después, en la década de 1970, David R. Cox introdujo el modelo de regresión de Cox, que incluyó la función de riesgo, h(t). Este modelo se convirtió en una herramienta poderosa en el análisis de supervivencia, especialmente en la presencia de covariables confusoras.
21.3.1 Función de Supervivencia (S(t))
Describe la probabilidad de que un evento no ocurra antes de un tiempo t definido. En otras palabras, S(t) es la probabilidad de que un sujeto o un objeto sobreviva más allá del tiempo t sin experimentar el evento de interés.
21.3.2 Función de Riesgo (Hazard Function o h(t))
Describe la tasa instantánea a la que ocurre el evento en un momento dado t, dado que el evento aún no ha ocurrido hasta ese momento. En otras palabras, h(t) representa la probabilidad condicional de que ocurra el evento en un intervalo de tiempo muy pequeño alrededor de t, dado que no ha ocurrido antes de t.
Nota: Es importante notar que, a diferencia de la función de supervivencia, que se enfoca en la probabilidad de no experimentar un evento, la función de riesgo se enfoca en la probabilidad de que ocurra el evento, es decir, en el fallo. En este sentido, podríamos decir que la función de riesgo presenta una perspectiva inversa de la información que nos brinda la función de supervivencia.
21.4 Tipos de análisis de supervivencia
21.4.1 Tablas de vida
Las tablas de vida es uno de los métodos tradicionales para analizar la supervivencia en una muestra de pacientes homogénea. Una de las aplicaciones más frecuentes es en el análisis de mortalidad por edades en estudios demográficos, por lo cual también son conocidas como tablas de mortalidad. Estas tablas permiten resumir información sobre la probabilidad de supervivencia a un evento considerando las censuras e intervalos de tiempo arbitrarios.
Estudio de caso
Exploraremos rápidamente la base de datos cancer antes de realizar nuestros análisis.
glimpse(cancer)Rows: 228
Columns: 10
$ inst <dbl> 3, 3, 3, 5, 1, 12, 7, 11, 1, 7, 6, 16, 11, 21, 12, 1, 22, 16…
$ time <dbl> 306, 455, 1010, 210, 883, 1022, 310, 361, 218, 166, 170, 654…
$ status <dbl> 2, 2, 1, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, …
$ age <dbl> 74, 68, 56, 57, 60, 74, 68, 71, 53, 61, 57, 68, 68, 60, 57, …
$ sex <dbl> 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 2, 1, …
$ ph.ecog <dbl> 1, 0, 0, 1, 0, 1, 2, 2, 1, 2, 1, 2, 1, NA, 1, 1, 1, 2, 2, 1,…
$ ph.karno <dbl> 90, 90, 90, 90, 100, 50, 70, 60, 70, 70, 80, 70, 90, 60, 80,…
$ pat.karno <dbl> 100, 90, 90, 60, 90, 80, 60, 80, 80, 70, 80, 70, 90, 70, 70,…
$ meal.cal <dbl> 1175, 1225, NA, 1150, NA, 513, 384, 538, 825, 271, 1025, NA,…
$ wt.loss <dbl> NA, 15, 15, 11, 0, 0, 10, 1, 16, 34, 27, 23, 5, 32, 60, 15, …De acuerdo a la exploración, reasignaremos los valores en la variable status, de tal manera que los pacientes muertos sean codificados como 1 (status=1) y los censurados como 0 (status=0). Adicionalmente, convertiremos a factor todas las variables categóricas y re-codificaremos sus niveles para que tengan solo 1 y 0.
cancer_clean <- cancer %>%
mutate(
sex = case_when(sex == 2 ~ 0,
TRUE ~ sex),
status = case_when(status == 2 ~ 1,
status == 1 ~ 0,
TRUE ~ status),
sex = factor(sex,
levels = c(0,1),
labels = c("Femenino", "Masculino")),
ph.ecog = factor(ph.ecog,
levels = c(0,1,2,3),
labels = c("Asintomático",
"Sintomático ambulatorio",
"En cama - 50% del dia",
"En cama + 50% del dia")))El objeto cancer_clean contiene las variables en el formato correcto para poder hacer la tabla de vida. Para ello, utilizaremos la función lifeTable del paquete discSurv y ajustaremos los argumentos “tiempo de supervivencia” (timeColumn) y “ocurrencia del evento” (eventColumn) con las variables correspondientes en nuestra base de datos.
A continuación, analizamos una tabla de vida con intervalos de longitud 1, comenzando desde [0, 1) como el primer intervalo y sucesivamente [1, 2), [2, 3), etc. En esta tabla, también observaremos las estimaciones puntuales de la función de riesgo (hazard) y la función de supervivencia (S), junto con sus respectivas desviaciones estándar.
lftable <- lifeTable(cancer_clean, timeColumn = "time", eventColumn = "status") Según los datos de la tabla de vida, el primer evento se registró en el intervalo [4, 5). Por lo que automáticamente el hazard cambiará con respecto al intervalo anterior. El cálculo del hazard en la tabla de vida se realiza dividiendo el número de eventos registrados para el periodo entre el número de individuos en riesgo para ese mismo periodo (events/atRisk). Para el intervalo [4, 5) el cálculo del hazard es 0.0044 (hazard = 1/228), este valor será útil para calcular la supervivencia (S = 1 - hazard), que para dicho periodo es 0.9956 (S = 1 - 0.0044).
A continuación, se adjunta una tabla que explica el significado de cada una de las variables que conforman la tabla de vida.
| Nombre | Notación |
|---|---|
| Número de individuos en riesgo en un intervalo de tiempo determinado (valor íntegro) | n |
| Número de eventos observados en un intervalo de tiempo determinado (valor íntegro) | events |
| Número de censuras en un intervalo de tiempo determinado (valor íntegro) | dropouts |
| Número estimado de individuos en riesgo con corrección de censurados (valor numérico) | atRisk |
| Riesgo estimado de muerte (sin covariables) en un intervalo de tiempo determinado | hazard |
| Desviación estándar estimada del hazard estimado | seHazard |
| Curva de supervivencia estimada | S |
| Desviación estándar estimada de la función de supervivencia estimada | seS |
| Estimado de la función acumulativa de hazard | cumHazard |
| Desviación estándar estimada de la función de riesgo acumulativo estimada | seCumHazard |
| Probabilidad marginal estimada del evento en el intervalo de tiempo | margProb |
Considerar que las estimaciones de la función de supervivencia o la tasa de supervivencia varían según el intervalo de tiempo que se elija en la tabla de vida. Cuando los intervalos son muy cortos y numerosos, el proceso de cálculo se torna complicado y no se obtienen plenamente los beneficios de usar la tabla de vida. Por otro lado, al emplear intervalos de tiempo prolongados, existe la posibilidad de que las estimaciones puedan carecer de precisión, por lo que se recomienda no usar intervalo de tiempo largo.
21.4.2 Kaplan-Meier
Es el método más usado en análisis de supervivencia. Estima la probabilidad condicional de supervivencia hasta el próximo evento de falla basada en la acumulación de tiempos de falla observados.
Las estimaciones de Kaplan-Meier se caracterizan por su capacidad para adaptarse a la presencia de censuras y proporcionar estimaciones de la probabilidad de supervivencia en intervalos de tiempo específicos. Estas estimaciones tienen en cuenta la información disponible hasta un punto determinado en el tiempo y se utilizan comúnmente en estudios de supervivencia y análisis de tiempo hasta eventos, como en estudios clínicos para evaluar la eficacia de tratamientos médicos.
Tiene 3 supuestos principales:
Todos los individuos (inclusive los que se unieron tarde al estudio) tienen la misma posibilidad de supervivencia.
El evento debe ocurrir en un momento específico del tiempo. Por ejemplo, se espera que todos los pacientes desarrollen cáncer de colon durante el periodo de evaluación.
Los pacientes censurados deben tener el mismo riesgo de que ocurra el evento y su censura no depende del resultado.
Con la misma base de datos ejecutaremos el análisis de Kaplan-Meier, para graficar la curva de supervivencia.
Inicialmente, calcularemos la función de supervivencia para toda la base de datos sin ninguna variable que sirva como estrato. Es por ello que en la fórmula de la función Surv, utilizaremos el número 1 que representará a la variable que estratificaría el análisis. También utilizaremos la función survfit que nos permitirá crear la curva de supervivencia.
En la tabla de Kaplan-Meier, los tiempos representan los momentos en los que se observó el evento de interés. La tabla también muestra que el primer evento ocurre en el tiempo t = 5. En este punto, la probabilidad de supervivencia se calcula restando la supervivencia inicial (100%) al cociente del número de eventos en ese tiempo y el número de personas en riesgo (1/228). Esto da como resultado una probabilidad de supervivencia de 0.9956 en ese intervalo de tiempo.
autoplot(km_curve, surv.colour = "#03595C") +
labs(x = "Tiempo", y = "Función de Supervivencia",
title = "Supervivencia de pacientes con cáncer de pulmón avanzado") +
theme_minimal()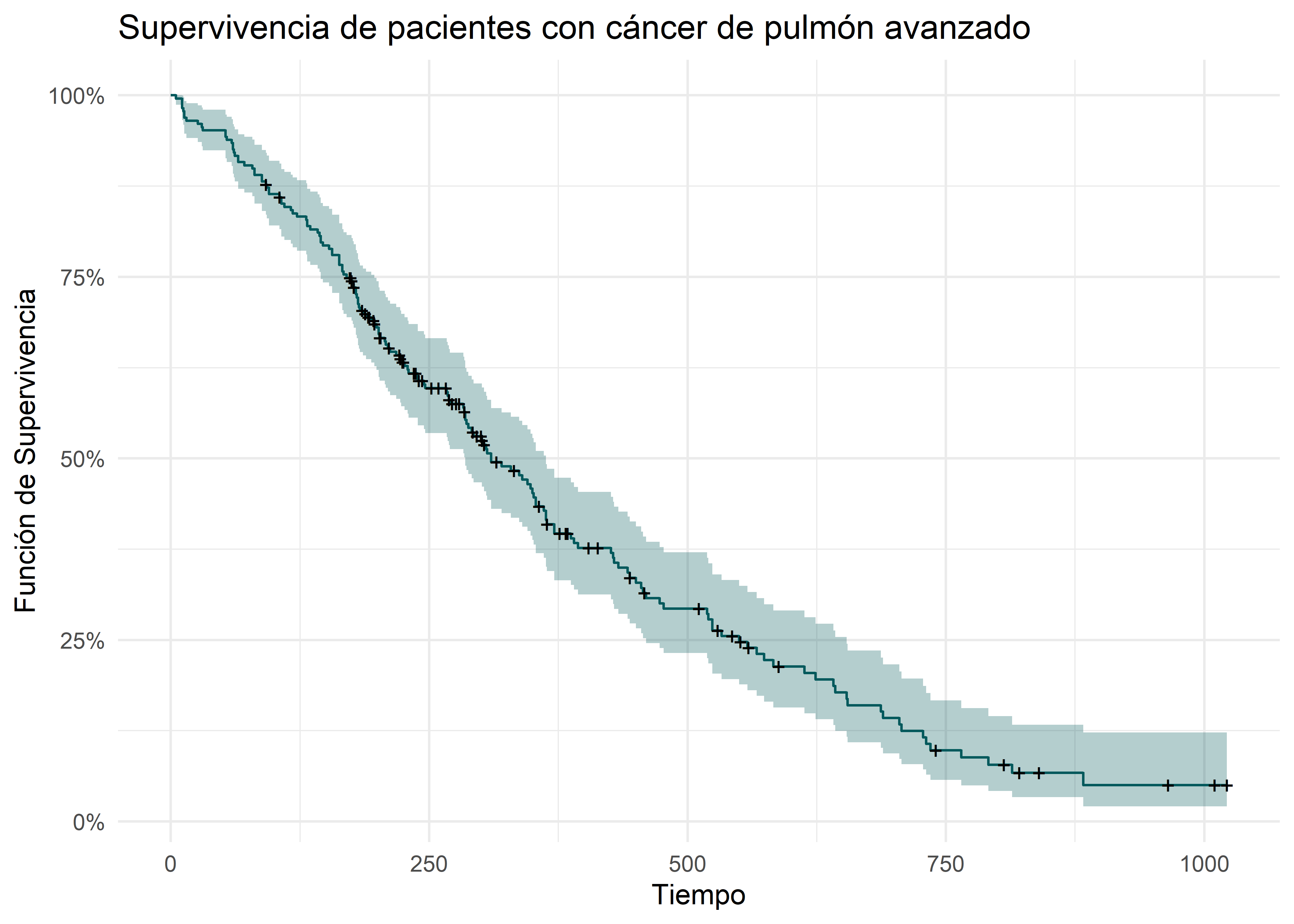
Con apoyo de la tabla resultante del análisis de Kaplan-Meier, y el gráfico de la función de supervivencia de pacientes con cáncer de pulmón avanzado, podemos describir que a los 310 días, el 50% de los individuos que iniciaron el estudio aún seguían vivos, y a los 883 días, tan solo el 5.03% de la población había sobrevivido al cáncer de pulmón avanzado.
Ahora que sabemos la curva de supervivencia en todo el periodo de estudio, observaremos si varía cuando el análisis se estratifica por sexo.
En la tabla de Kaplan-Meier, estratificada por sexo, se pueden apreciar diferencias en el inicio de los eventos entre mujeres y hombres. En el caso de las mujeres, los eventos iniciaron en el día 5, mientras que para los hombres, este inicio ocurrió en el día 11. Además, al final del período de seguimiento del estudio, se observa que la probabilidad de supervivencia en hombres (0.0357) fue inferior a la de las mujeres (0.0832). Para detallar esto, utilizaremos un gráfico de Kaplan-Meier estratificado por la variable sexo.
autoplot(km_sex_curve, surv.alpha = 0.8, conf.int.alpha = 0.4) +
labs(x = "Tiempo",
y = "Función de Supervivencia",
title = "Supervivencia de pacientes con cáncer de pulmón avanzado") +
scale_fill_lancet() +
scale_color_lancet() +
theme_minimal()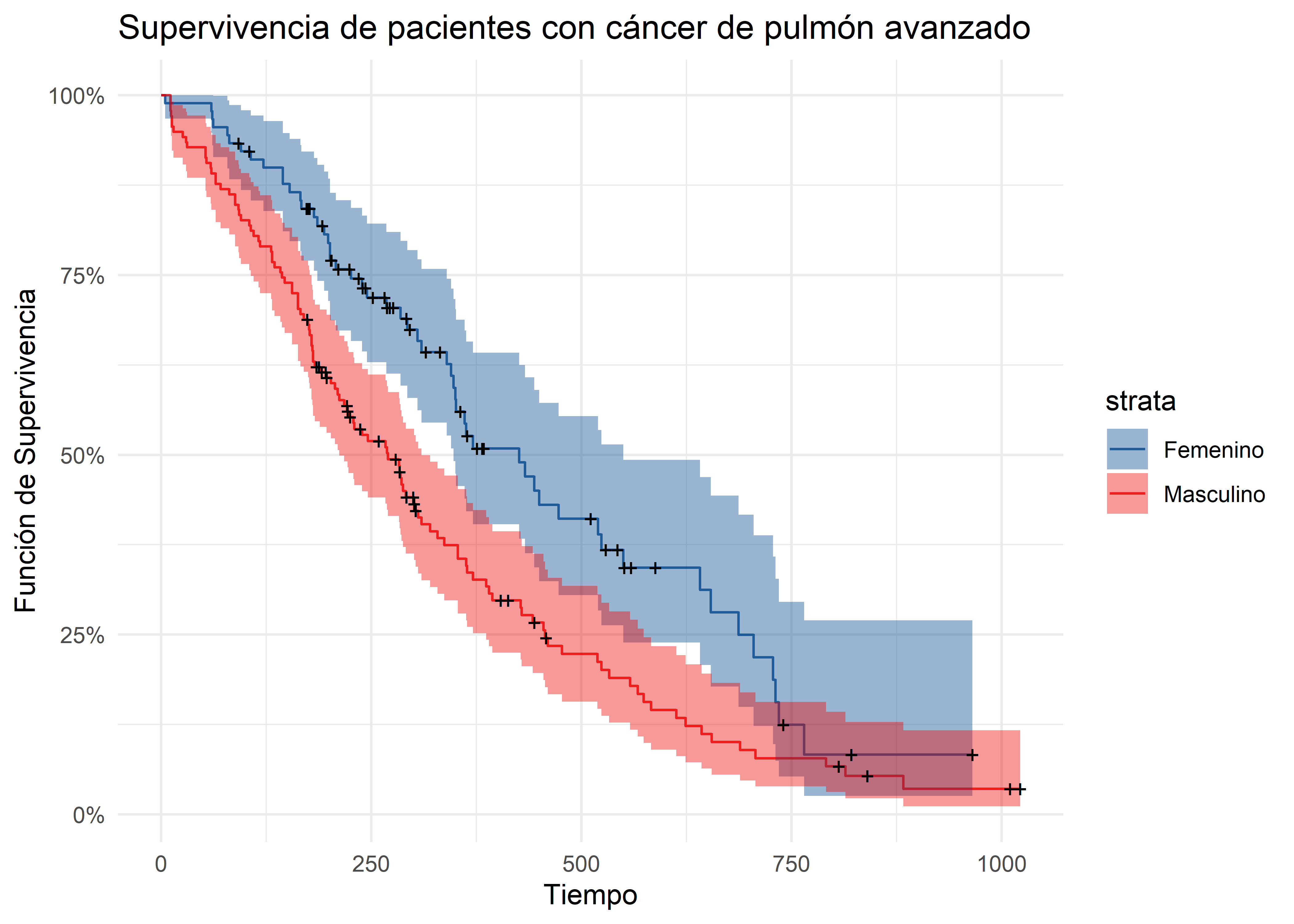
Las curvas de supervivencia obtenidas del análisis de KM estratificado por sexo, revelan que la supervivencia fue ligeramente mayor en las mujeres a comparación de los hombres. En el grupo de los hombres, la supervivencia llegó al 50% en el día 269, mientras que para las mujeres el mismo valor de supervivencia se observó en el día 371.
21.4.3 Modelo de riesgos proporcionales de Cox
La regresión de Cox es método estadístico que estima el Hazard Ratio (HR) o cociente de riesgos instantáneos, el cual compara las tasas de riesgo de dos grupos o categorías diferentes en relación con la ocurrencia de un evento específico.
La característica clave de la regresión de Cox es que no hace suposiciones específicas sobre la forma de la distribución de supervivencia de los datos, lo que la hace muy flexible. En cambio, se basa en la idea de “riesgos proporcionales”, lo que significa que asume que el cociente de riesgos (hazard ratio) entre dos grupos es constante con el tiempo.
Tiene 3 supuestos importantes:
La supervivencia de los individuos es independiente.
A medida que incrementa el predictor (tiempo), aumenta la probabilidad de que ocurra el evento.
El riego de proporcionalidad debe ser constante. Este se puede comprobar inspeccionando la curva de supervivencia o con prueba de residuos de Schoenfeld.
Es importante mencionar que la regresión de Cox permite ajustar el estimado incluyendo covariables al modelo de regresión, de esta manera se evalúa si las covariables afectan la tasa de riesgo de que ocurra el evento en cuestión.
La función que utilizaremos será coxph del paquete survival.
Interpretación del coeficiente de sexo:
En la población de pacientes con cáncer de pulmón avanzado, el hazard de morir en los hombres es 1.73 (IC95%: 1.24 - 2.40) veces el hazard de morir en las mujeres, ajustando por edad y escala funcional ECOG. Este resultado es estadísticamente significativo con un p-valor de 0.001.
Ahora graficaremos la curva de supervivencia obtenida con el modelo de riesgos proporcionales de Cox.
cox_curve <- survfit(cox)
autoplot(cox_curve, surv.colour = "#DC4326") +
labs(x = "Tiempo",
y = "Función de Supervivencia",
title = "Supervivencia de pacientes \n con cáncer de pulmón avanzado") +
theme_minimal()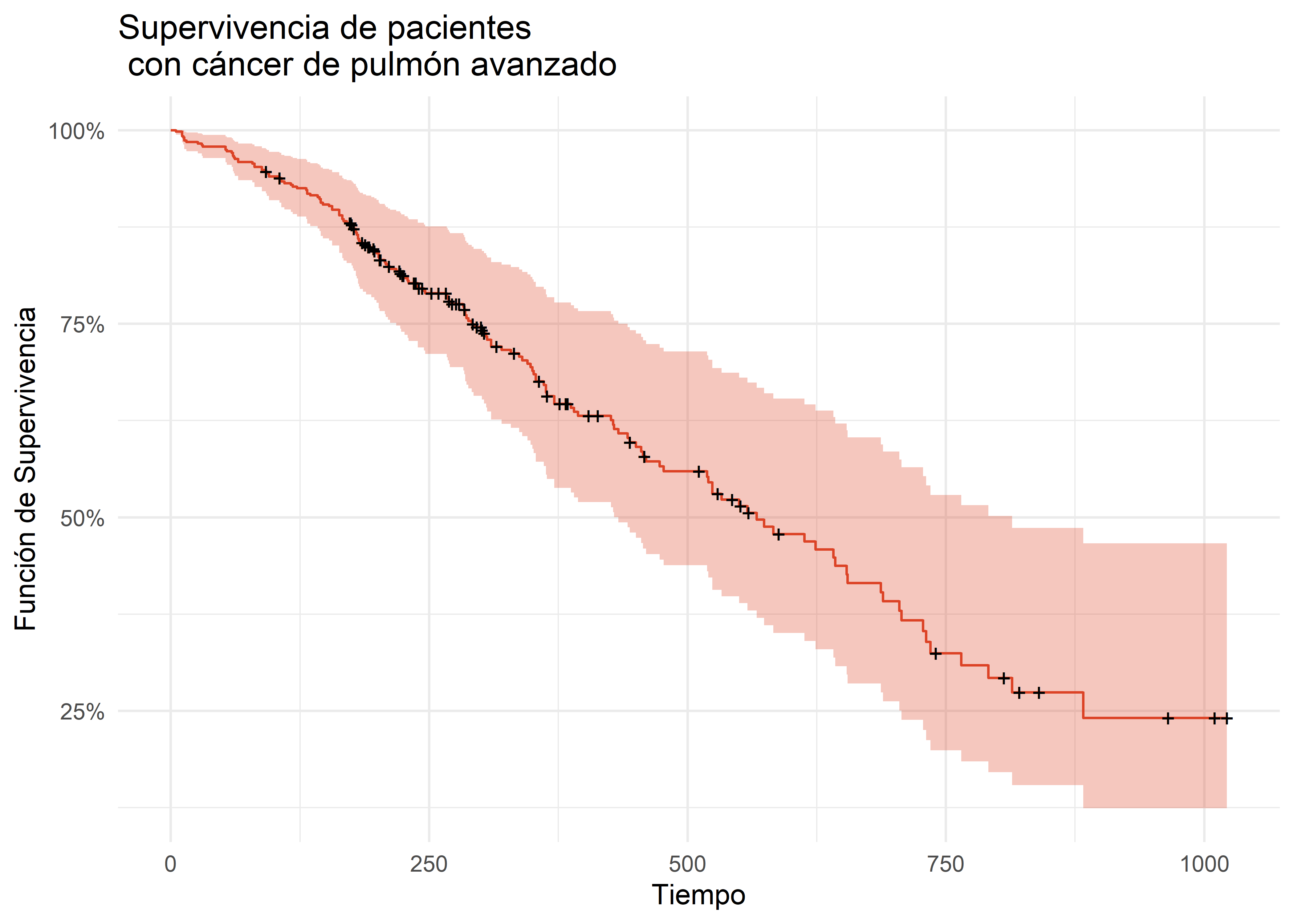
Una vez que hayamos corrido el modelo, podríamos revisar si el supuesto de riesgos proporcionales se cumple. Para ello, utilizaremos la función cox.zph del paquete survival.
cox.zph(cox) chisq df p
sex 2.406 1 0.12
age 0.163 1 0.69
ph.ecog 5.650 3 0.13
GLOBAL 7.777 5 0.17Los valores p de cada uno de los coeficientes son no significativos, lo que significaría que los hazards se mantienen proporcionales.
Finalmente, utilizaremos la prueba global de Schoenfeld, también conocida como prueba de residuos de Schoenfeld. Esta prueba examina si existe una relación significativa entre estos residuos de Schoenfeld y el tiempo. En otras palabras, verifica si hay evidencia de que las razones de riesgo cambian con el tiempo.
ggcoxzph(cox.zph(cox), point.size = 1, ggtheme = theme_classic())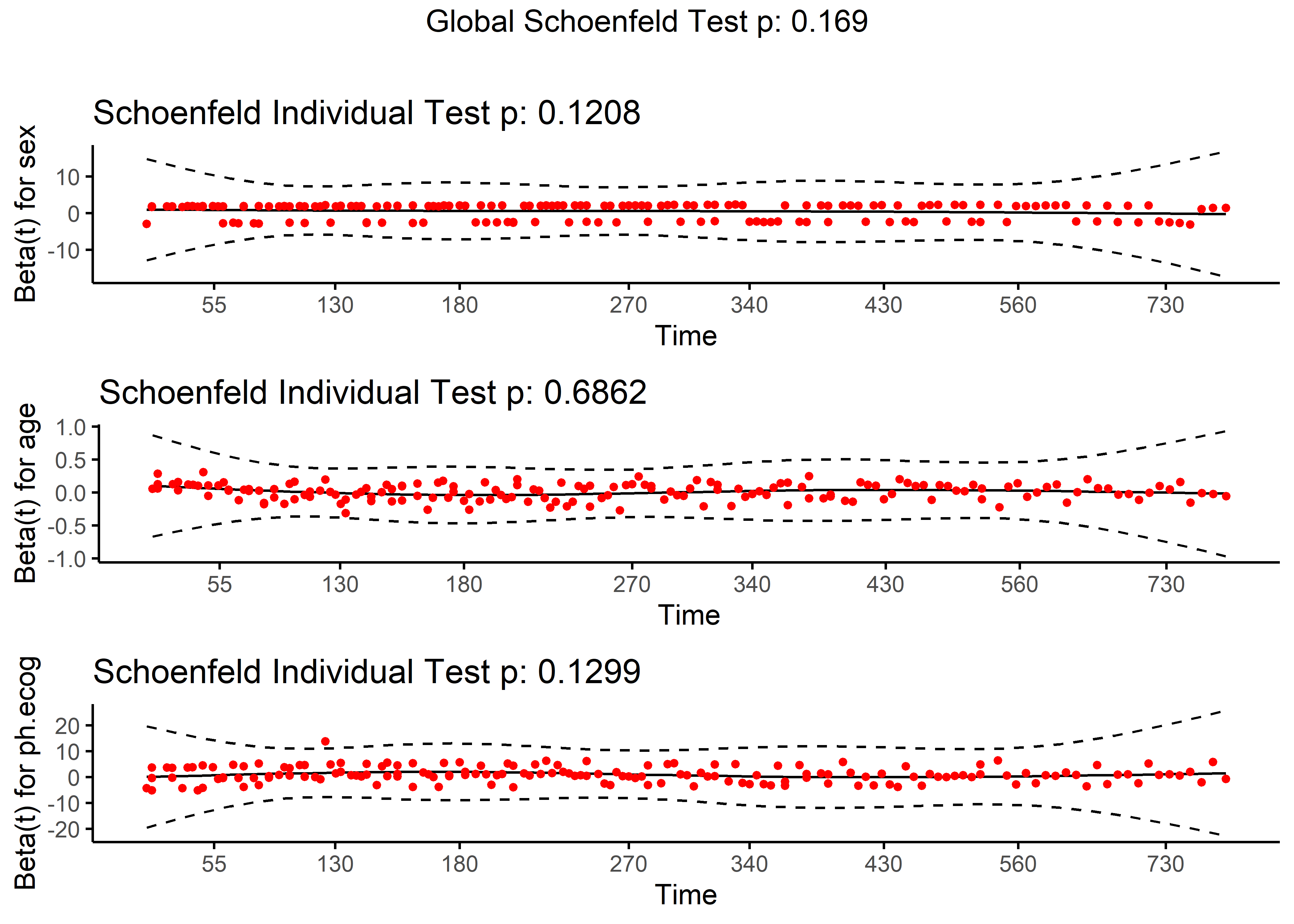
Del gráfico concluimos que los residuos son independientes del tiempo y por lo tanto, la suposición de riesgos proporcionales se cumple.
21.5 Ejercicios
21.5.1 Ejercicio 1
Evalúe el análisis de supervivencia de cáncer pulmonar usando la base de datos cancer, estratificado por edad menor o igual a 70 años y mayor de 70 años.
21.5.2 Ejercicio 2
Realice un gráfico de Kaplan-Meier estratificado por edad menor o igual a 70 años y mayor de 70 años.