18 Estudios transversales
18.1 Paquetes y Data
Los paquetes que utilizaremos para este capítulo serán los siguientes,
covid_mex <- read_csv("data/covid_mexico_2.csv")18.2 Diseño de estudio
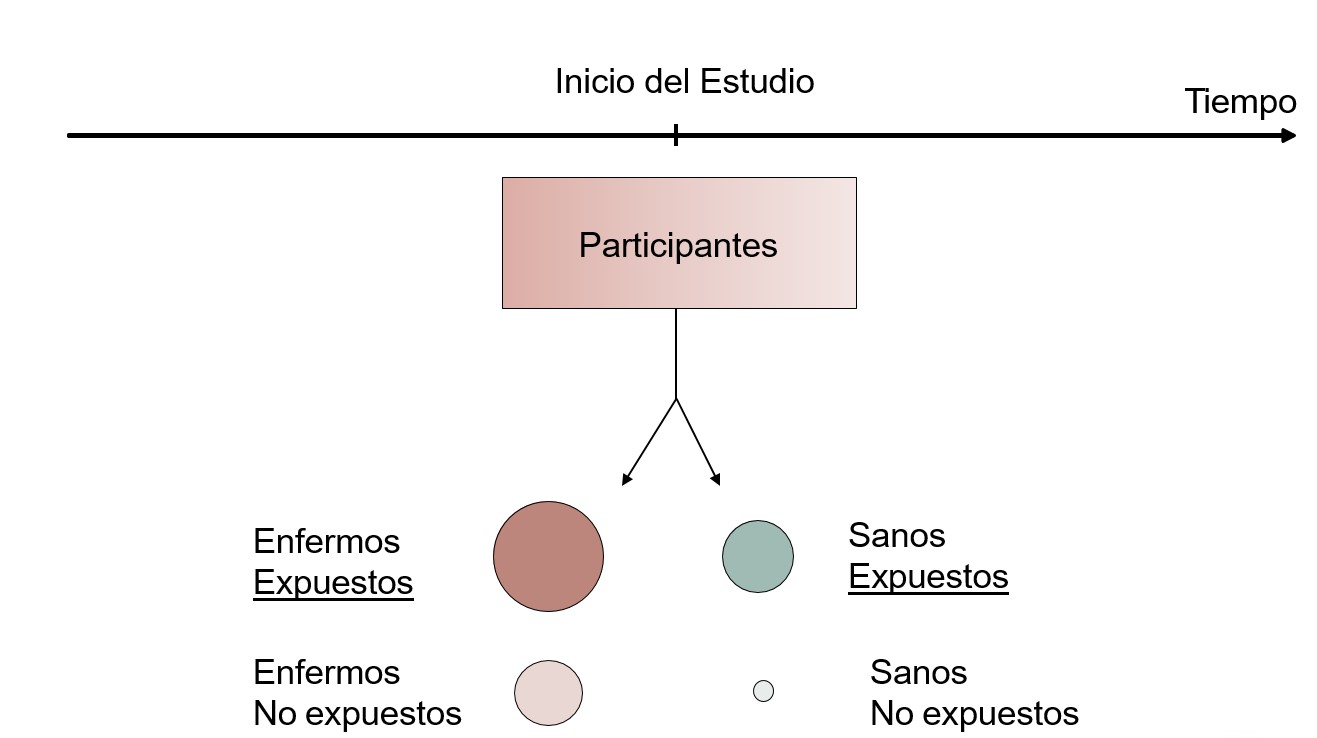
Los estudios de diseño transversal son aquellos en los que la exposición y el desenlace se miden de manera simultánea, sin realizar un seguimiento posterior. En consecuencia, este diseño es útil para determinar la prevalencia de una enfermedad y/o la asociación entre variables independientes y la variable desenlace.
18.3 Medidas de asociación en estudios transversales
En un estudio transversal, las dos medidas de asociación más comunes son la Razón de Prevalencia (RP) y el Odds Ratio (OR). La RP evalúa la proporción de casos de una enfermedad en el grupo expuesto en comparación con el grupo no expuesto en un punto en el tiempo y es especialmente adecuada para enfermedades comunes. Por otro lado, el OR compara las probabilidades de un evento entre grupos expuestos y no expuestos, siendo útil para eventos raros o cuando la prevalencia del evento es baja. En este capítulo, realizaremos el cálculo de ambas medidas mediante análisis de regresión.
18.3.1 Razón de Prevalencias
Recordemos que la razón de prevalencia es una medida de asociación que compara la prevalencia de la enfermedad en el grupo de expuestos y la prevalencia de la enfermedad en el grupo de no expuestos.
Se puede representar de la siguiente manera,
La estimación de la Razón de Prevalencia (RP) puede llevarse a cabo utilizando distintos enfoques, entre los cuales destacan dos modelos: la Regresión de Poisson y la Regresión Log-binomial. La Regresión de Poisson se basa en el análisis de datos de conteo o prevalencia, mientras que la Regresión Log-binomial calcula directamente el valor de la RP. No obstante, es importante señalar que estos modelos pueden presentar dificultades de convergencia.
Para superar estas limitaciones, Zou (2004) propone una alternativa en la forma de un modelo de Regresión de Poisson modificado, conocido como Poisson Modificado. Este enfoque incorpora estimaciones de errores robustos, lo que contribuye a una mayor estabilidad en el proceso de estimación.
18.3.2 Modelo de regresión de Poisson modificado
El modelo de regresión de Poisson es uno de los modelos lineales generalizados (GLM) que es usado para modelar datos de conteo en un determinado intervalo de tiempo como el número de atenciones cirugías ambulatorias en los hospitales de Lima durante el mes de Julio de 2023, el número de casos de malaria por semana epidemiológica en los establecimientos de salud de Loreto en el año 2021, entre otros. Al modelar datos de conteo, esperamos trabajar con números enteros no negativos.
El modelo de regresión de Poisson puede ser expresado matemáticamente de la siguiente manera,
Donde:
-
-
-
Para ajustar el modelo de regresión de Poisson, utilizamos técnicas estadísticas, como la máxima verosimilitud, el cual estimará los valores de los coeficientes de regresión (
Después de ajustar el modelo, obtendremos los siguientes resultados:
18.3.2.1 Ejercicio
Para este ejercicio, utilizaremos el objeto covid_mex, el cual contiene una muestra de la base de datos de los resultados del test RT-PCR de COVID-19 en México, entre abril y junio de 2020. La base de datos oficial contiene variables sociodemográficas como sexo, edad, lugar de origen, condición de migrante; y también variables clínicas como obesidad, diabetes, inmunosupresión, asma, epoc, hipertensión, entre otras. La base de datos cruda puede ser accedida a través de la página oficial de la Dirección General de Epidemiología o también pueden encontrarla procesada aquí.
El objetivo de este ejercicio es estimar la razón de prevalencias de pacientes diagnosticados con COVID-19 en UCI y con antecedente de obesidad, ajustando por sexo, edad categorizada, asma y tabaquismo. Para ello, haremos una exploración rápida de la base de datos.
glimpse(covid_mex)Rows: 2,600
Columns: 7
$ RESULTADO <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
$ UCI <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,…
$ TABAQUISMO <dbl> 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ SEXO <dbl> 2, 2, 2, 2, 1, 1, 2, 2, 2, 1, 2, 1, 1, 2, 1, 2, 2, 2, 2, 1,…
$ ASMA <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ OBESIDAD <dbl> 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0,…
$ EDAD <dbl> 56, 52, 75, 76, 51, 73, 71, 48, 68, 48, 50, 71, 56, 39, 62,…Ahora podemos saber que la base de datos covid_mex cuenta con 2600 observaciones, 7 variables, y que ninguna de las variables son de tipo factor. Es por ello que, debemos manipular las variables antes de introducirlas al modelo de regresión. Pero antes de ello, verificaremos que las variables que deberían ser dicotómicas tengan realmente dos valores. La variable EDAD es numérica por naturaleza, por lo tanto, no evaluaremos valores únicos y la variable RESULTADO solo tendrá un valor único debido a que solo nos hemos enfocado en los pacientes positivos a SARS-CoV-2.
unique(covid_mex$TABAQUISMO)[1] 0 1unique(covid_mex$SEXO)[1] 2 1unique(covid_mex$ASMA)[1] 0 1unique(covid_mex$OBESIDAD)[1] 1 0unique(covid_mex$UCI)[1] 0 1A continuación se muestra el diccionario de la base de datos covid_mex.
| Variable | Notación |
|---|---|
| Resultado | 1 = Positivo |
| UCI | 1 = UCI, 0 = No UCI |
| TABAQUISMO | 1 = Fumador, 0 = No Fumador |
| SEXO | 2 = Femenino, 1 = Masculino |
| ASMA | 1 = Asmatico, 0 = No Asmatico |
| OBESIDAD | 1 = Obeso, 0 = No Obeso |
| EDAD | Edad en años |
Con la información proporcionada en la tabla anterior, procederemos a convertir las variables correspondientes a factor. Adicionalmente, debemos recordar que en el modelo final debemos incluir la edad categorizada teniendo en cuenta los siguientes rangos: “0-10”, “11-20”, “21-30”, “31-40”, “41 - +”.
covid_mex_clean <- covid_mex %>%
mutate(
SEXO = case_when(
SEXO == 1 ~ 1,
TRUE ~ 0
),
EDAD_CAT = case_when(
EDAD < 11 ~ 0,
EDAD < 21 ~ 1,
EDAD < 31 ~ 2,
EDAD < 41 ~ 3,
TRUE ~ 4
),
TABAQUISMO = factor(
TABAQUISMO,
levels = c(0, 1),
labels = c("No Fumador", "Fumador")
),
SEXO = factor(
SEXO,
levels = c(0, 1),
labels = c("Femenino", "Masculino")
),
ASMA = factor(
ASMA,
levels = c(0,1),
labels = c("No Asmatico", "Asmatico")
),
OBESIDAD = factor(
OBESIDAD,
levels = c(0,1),
labels = c("No Obeso", "Obeso")
),
EDAD_CAT = factor(
EDAD_CAT,
levels = c(0,1,2,3,4),
labels = c("0-10", "11-20", "21-30", "31-40", "41 - +")
)
) %>%
select(-EDAD)Con la base de datos final, podemos realizar tablas o gráficos exploratorios sobre las variables para evaluar su distribución.
covid_mex_clean %>%
cross_tbl(by = "SEXO") %>%
theme_pubh()|
Femenino, N = 1,640 |
Masculino, N = 960 |
Overall, N = 2,600 |
|
|---|---|---|---|
| RESULTADO | 1,640 (100%) | 960 (100%) | 2,600 (100%) |
| UCI | 114 (7.0%) | 50 (5.2%) | 164 (6.3%) |
| TABAQUISMO | |||
| No Fumador | 1,444 (88%) | 926 (96%) | 2,370 (91%) |
| Fumador | 196 (12%) | 34 (3.5%) | 230 (8.8%) |
| ASMA | |||
| No Asmatico | 1,612 (98%) | 923 (96%) | 2,535 (98%) |
| Asmatico | 28 (1.7%) | 37 (3.9%) | 65 (2.5%) |
| OBESIDAD | |||
| No Obeso | 1,271 (78%) | 723 (75%) | 1,994 (77%) |
| Obeso | 369 (23%) | 237 (25%) | 606 (23%) |
| EDAD_CAT | |||
| 0-10 | 12 (0.7%) | 9 (0.9%) | 21 (0.8%) |
| 11-20 | 3 (0.2%) | 7 (0.7%) | 10 (0.4%) |
| 21-30 | 66 (4.0%) | 45 (4.7%) | 111 (4.3%) |
| 31-40 | 190 (12%) | 99 (10%) | 289 (11%) |
| 41 - + | 1,369 (83%) | 800 (83%) | 2,169 (83%) |
Un total de 2600 participantes fueron incluidos en el análisis. Las mujeres presentaron hábitos tabáquicos en mayor proporción que los hombres (12% vs. 3.5%). Adicionalmente, reportaron una mayor frecuencia de ingreso a UCI (7.0%). Finalmente, se encontraron frecuencias bastante similares entre hombres y mujeres para las variables de obesidad, asma y grupos etarios.
covid_mex_clean %>%
mutate(
UCI = factor(UCI, levels = c(0,1), labels = c("No UCI", "UCI"))
) %>%
ggplot() +
geom_mosaic(aes(x = product(SEXO), fill = EDAD_CAT)) +
scale_fill_npg() +
facet_wrap("UCI") +
ggtitle("Ingreso a UCI por sexo y grupo etario") +
theme_minimal() +
theme(
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
axis.text.y=element_blank(),
axis.ticks.y=element_blank(),
axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1)
) +
labs(fill = "Grupo Etario", x = "Sexo", y = "Proporción")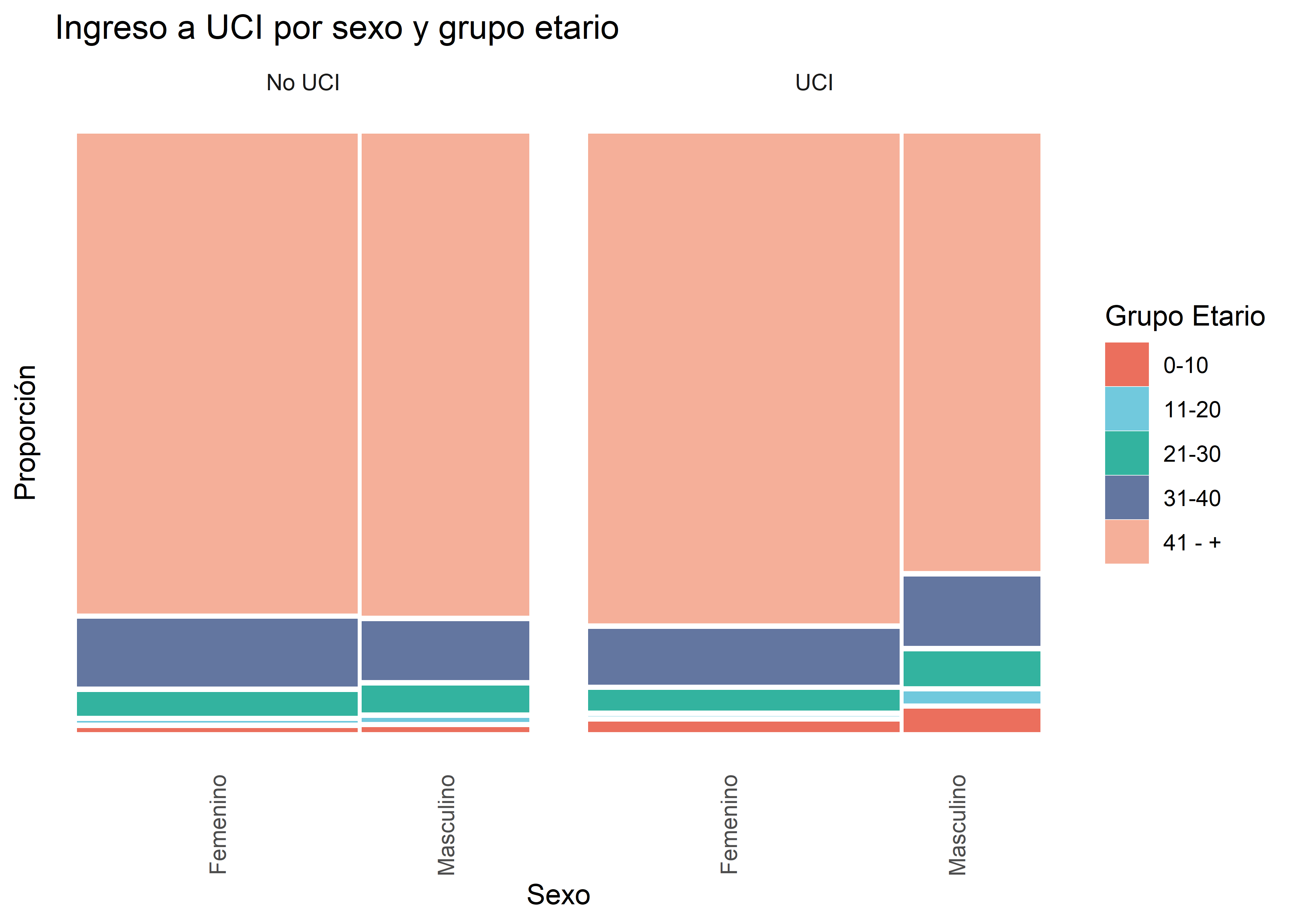
Podemos observar que en el grupo de pacientes que no ingresó a la unidad de cuidados intensivos, las proporciones se mantienen bastante similares en ambos sexos, mientras que en el gráfico de la derecha, se reportó una mayor proporción de mujeres de 41 o más años de edad ingresando a UCI en comparación a los hombres del mismo rango de edad.
Una vez terminada la exploración rápida de los datos, realizaremos el modelo de regresión de Poisson. Recordemos que estamos interesados en reportar la razón de prevalencias de ingreso a UCI en pacientes con antecedente de obesidad ajustando por sexo, edad categorizada, asma y tabaquismo. Para ello, deberemos primero filtrar a todos los pacientes positivos a SARS-CoV-2. Y posteriormente correr el modelo de regresión. Finalmente, deberemos exponenciar los coeficientes de la regresión para eliminar el logaritmo. Con la función tidy del paquete broom, podemos obtener los coeficientes exponenciados si configuramos el argumento exponientiate = TRUE.
model_poisson <- glm(
UCI ~ OBESIDAD + SEXO + EDAD_CAT + ASMA + TABAQUISMO,
family = poisson(link="log"),
data = covid_mex_clean
)
model_poisson
Call: glm(formula = UCI ~ OBESIDAD + SEXO + EDAD_CAT + ASMA + TABAQUISMO,
family = poisson(link = "log"), data = covid_mex_clean)
Coefficients:
(Intercept) OBESIDADObeso SEXOMasculino EDAD_CAT11-20
-1.5641 0.3948 -0.3057 -0.5775
EDAD_CAT21-30 EDAD_CAT31-40 EDAD_CAT41 - + ASMAAsmatico
-1.2447 -1.3363 -1.2559 0.5717
TABAQUISMOFumador
0.1938
Degrees of Freedom: 2599 Total (i.e. Null); 2591 Residual
Null Deviance: 906.4
Residual Deviance: 891.1 AIC: 1237Ahora exponenciamos los coeficientes.
model_poisson_exp <- broom::tidy(model_poisson, conf.int = T, exponentiate = T)
model_poisson_exp# A tibble: 9 × 7
term estimate std.error statistic p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.209 0.504 -3.11 0.00190 0.0646 0.491
2 OBESIDADObeso 1.48 0.171 2.30 0.0212 1.05 2.06
3 SEXOMasculino 0.737 0.173 -1.77 0.0766 0.521 1.03
4 EDAD_CAT11-20 0.561 1.12 -0.516 0.606 0.0287 3.81
5 EDAD_CAT21-30 0.288 0.629 -1.98 0.0479 0.0866 1.10
6 EDAD_CAT31-40 0.263 0.559 -2.39 0.0167 0.0966 0.917
7 EDAD_CAT41 - + 0.285 0.510 -2.46 0.0137 0.119 0.930
8 ASMAAsmatico 1.77 0.390 1.47 0.142 0.748 3.52
9 TABAQUISMOFumador 1.21 0.249 0.777 0.437 0.722 1.93 El objeto model_poisson_exp contiene una regresión de poisson original, la cual estima los errores estándar a través del método de máxima verosimilitud. Para obtener el modelo de Poisson modificado, debemos aplicar el estimador de errores sandwich o estimación de errores robustos. Para ello, haremos uso de la función summ del paquete jtools.
model_poisson_mod_exp <- summ(model_poisson, robust = "HC1", confint = T, digits = 3, exp = T)
tidy(model_poisson_mod_exp) %>%
datatable(
options = list(
display = "compact",
pageLength = 10,
scrollX = TRUE
)
)Si comparamos los coeficientes de la regresión de Poisson y la regresión de Poisson modificada, no observaremos ningún cambio, ya que, el cambio solo se ha realizado en la estimación de los errores estándar. Sin embargo, si centramos la comparación en los intervalos de confianza, sí podremos observar un cambio. El cálculo de los errores estándar robustos ha reducido los intervalos de confianza a comparación de la estimación de los errores con el método de máxima verosimilitud.
Interpretación del coeficiente de Obesidad:
En la población de pacientes mexicanos con COVID-19, la proporción de personas que ingresaron a UCI en el grupo de obesos fue 1.48 (IC95%: 1.07 - 2.05) veces la proporción de personas que ingresaron a UCI en el grupo de no obesos, ajustando por sexo, edad categorizada, condición de asma y hábito tabáquico. Este resultado fue estadísticamente significativo con un p-valor de 0.017.
18.3.3 Odds Ratio
El Odds Ratio o Razón de Odds es la probabilidad de que el evento ocurra sobre la probabilidad de que el evento no ocurra en el grupo de expuestos, versus, la probabilidad de que el evento ocurra sobre la probabilidad de que el evento no ocurra en los no expuestos.
También puede ser expresado simplificadamente de la siguiente manera,
En un diseño transversal, si el evento de interés es raro o tiene una baja prevalencia en la población, el OR puede proporcionar una estimación precisa de la asociación. Usualmente, se utiliza el 10% como punto de corte para decidir si un evento es raro o poco frecuente. En la sección previa generamos una tabla con la distribución de las variables incluidas en el estudio, y pudimos observar que la proporción de pacientes en UCI fue de 6.3% en toda la muestra, lo que nos permite aplicar una regresión logística.
18.3.4 Regresión Logística
El OR puede ser calculado a través de un modelo de regresión logística en un estudio de diseño transversal, estimando la relación entre una variable desenlace dicotómica y una o más covariables que expliquen el evento de interés.
En esta sección, utilizaremos la misma estructura del modelo de regresión anterior pero esta vez utilizaremos una familia distinta de los modelos lineales generalizados (family = binomial).
Este sería el modelo teórico:
Donde logit() es la función de enlace no lineal que relaciona una expresión lineal de los predictores con la expectativa de la respuesta binaria:
Entonces el modelo sería,
Recordemos la estructura del modelo de regresión logística en R usando la función glm()
El argumento family establece la distribución de errores para el modelo, mientras que el argumento link relaciona los predictores con el valor esperado del resultado.
A diferencia del modelo de regresión de Poisson, para la regresión Logística, necesitaremos convertir la variable desenlace a tipo factor.
class(covid_mex_clean$UCI)[1] "numeric"La variable desenlance UCI por el momento es numérica, procederemos a manipularla para su posterior inclusión en el modelo de regresión propuesto.
Ahora comprobaremos que realmente se haya efectuado el cambio.
class(covid_uci_fct$UCI)[1] "factor"El objeto covid_uci_fct contiene todas las variables necesarias para nuestro análisis de regresión.
logistic_reg <- glm(
UCI ~ OBESIDAD + SEXO + EDAD_CAT + ASMA + TABAQUISMO,
family = binomial(link = "logit"),
data = covid_uci_fct
)
logistic_reg
Call: glm(formula = UCI ~ OBESIDAD + SEXO + EDAD_CAT + ASMA + TABAQUISMO,
family = binomial(link = "logit"), data = covid_uci_fct)
Coefficients:
(Intercept) OBESIDADObeso SEXOMasculino EDAD_CAT11-20
-1.3392 0.4260 -0.3276 -0.6836
EDAD_CAT21-30 EDAD_CAT31-40 EDAD_CAT41 - + ASMAAsmatico
-1.4067 -1.5045 -1.4186 0.6271
TABAQUISMOFumador
0.2105
Degrees of Freedom: 2599 Total (i.e. Null); 2591 Residual
Null Deviance: 1224
Residual Deviance: 1207 AIC: 1225Al igual que en el modelo de regresión de Poisson, es importante exponenciar los coeficientes de la regresión, de lo contrario no estaremos interpretando el odds, sino el logaritmo del odds.
logistic_reg_exp <- logistic_reg %>%
tidy(exponentiate = TRUE, conf.int = TRUE)
logistic_reg_exp %>%
datatable(
options = list(
display = "compact",
pageLength = 10,
scrollX = TRUE
)
)Interpretación del OR de Obesidad
En la población de pacientes mexicanos con COVID-19, el odds de ingresar a UCI en el grupo de obesos es 1.53 (IC95%: 1.07 - 2.16) veces el Odds en el grupo de no obesos, ajustando por sexo, edad categorizada, condición de asma y hábito tabáquico. Este resultado fue estadísticamente significativo con un valor p de 0.017.
Adicionalmente, deseamos saber si es que el coeficiente de exposición principal (EDAD_CAT = 41 - +). Para ello, debemos refactorizar la variable y correr nuevamente el análisis de regresión.
El nuevo dataset contiene a la categoría de edad 41 años a más (EDAD_CAT = 41 - +) como la categoría de referencia, y ahora sí podremos correr el análisis de regresión.
logistic_reg_2 <- glm(
UCI ~ OBESIDAD + SEXO + EDAD_CAT + ASMA + TABAQUISMO,
family = binomial(link = "logit"),
data = covid_uci_fct_rlvl
)
logistic_reg_2
Call: glm(formula = UCI ~ OBESIDAD + SEXO + EDAD_CAT + ASMA + TABAQUISMO,
family = binomial(link = "logit"), data = covid_uci_fct_rlvl)
Coefficients:
(Intercept) OBESIDADObeso SEXOMasculino EDAD_CAT0-10
-2.75784 0.42600 -0.32761 1.41863
EDAD_CAT11-20 EDAD_CAT21-30 EDAD_CAT31-40 ASMAAsmatico
0.73498 0.01198 -0.08591 0.62711
TABAQUISMOFumador
0.21055
Degrees of Freedom: 2599 Total (i.e. Null); 2591 Residual
Null Deviance: 1224
Residual Deviance: 1207 AIC: 1225Recordemos nuevamente que estamos trabajando con el logaritmo del odds. Por tal motivo, debemos exponenciar los coeficientes.
logistic_reg_2_exp <- logistic_reg_2 %>%
tidy(exponentiate = TRUE, conf.int = TRUE) %>%
datatable(
options = list(
display = "compact",
pageLength = 10,
scrollX = TRUE
)
)
logistic_reg_2_expEl
18.3.5 Visualización de Modelos
Ahora que tenemos todos los modelos ejecutados, podemos visualizar los coeficientes de todas las variables incluidas en el análisis junto con sus respectivos intervalos de confianza. Para fines prácticas solo utilizaremos 3 modelos:
- Modelo 1: Regresión de Poisson
- Modelo 2: Regresión de Poisson Modificado
- Modelo 3: Regresión Logística (sin el cambio de la categoría de referencia)
Para ello, primero deberemos unir todos los modelos en una sola base de datos. Por tal motivo, las columnas que queremos mantener en las tres bases de datos deben tener el mismo nombre. Si se dan cuenta, el objeto model_poisson_mod_exp no es un data frame, por lo que tendremos que manipularlo, y renombrar algunas de sus variables para que podamos unir todas las bases de datos sin ningún problema.
class(model_poisson_mod_exp)[1] "summ.glm" "summ" Comencemos con la manipulación de datos.
model_poisson_exp_viz <- model_poisson_exp %>%
mutate(model = "R. Poisson")
model_poisson_mod_exp_viz <- as_tibble(model_poisson_mod_exp$coeftable, rownames = "term") %>%
rename(conf.low ="2.5%") %>%
rename(conf.high = "97.5%") %>%
rename(estimate = "exp(Est.)") %>%
rename(p.value = "p") %>%
rename(statistic = "z val.") %>%
mutate(model = "R. Poisson Modificado")
logistic_reg_exp_viz <- logistic_reg_exp %>%
mutate(model = "R. Logistica")
model_results <- bind_rows(model_poisson_exp_viz, model_poisson_mod_exp_viz, logistic_reg_exp_viz)Cuando la base de datos contenga los tres modelos de regresión, procederemos a graficarlos utilizando el paquete ggplot.
ggplot(data = model_results,
aes(x = estimate, y = term, xmin = conf.low, xmax = conf.high,
color = model, shape = model)) +
scale_color_npg() +
geom_pointrange(position = position_dodge(width = 1.0)) +
labs(title = "Estimados de los modelos de UCI y Obesidad",
x = "Estimado",
y = "Predictor",
caption = "Error bars show the 95% confidence interval") +
scale_y_discrete(labels = c("Intercepto", "Asmatico", "Edad: 11-20", "Edad: 21-30", "Edad: 31-40", "Edad: 41 - +", "Obeso", "Masculino", "Fumador")) +
ggpubr::theme_pubclean()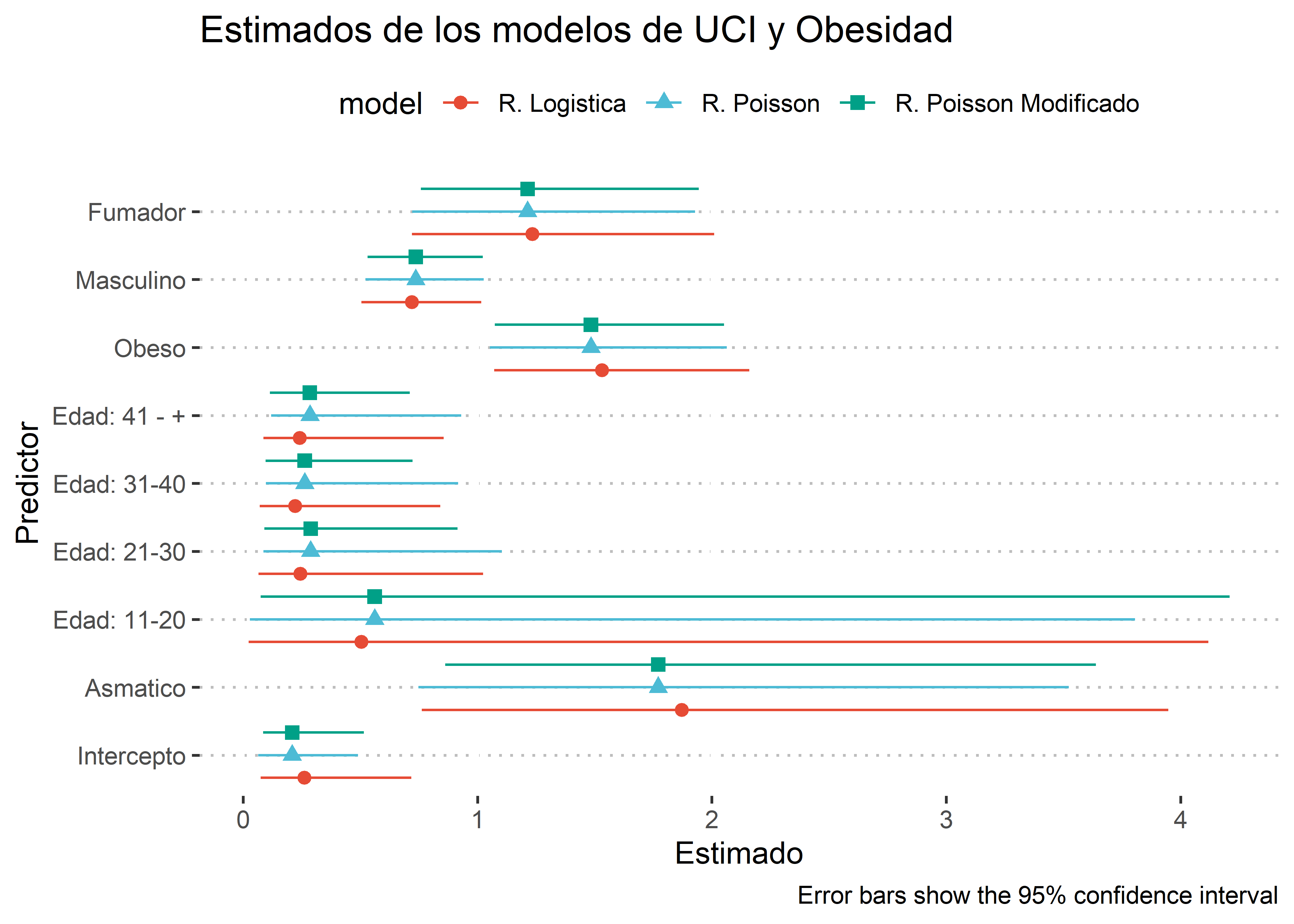
18.4 Ejercicios
18.4.1 Ejercicio 1
Elabore un modelo de regresión logístico incluyendo a la condición de UCI (UCI) como outcome y solo a las variables Sexo (SEX) y la condición de fumador (TABAQUISMO) como predictores. Exponencie los coeficientes de la regresión para obtener los OR.
18.4.2 Ejercicio 2
Elabore un modelo de regresión de Poisson Modificado incluyendo a la condición de UCI (UCI) como outcome y solo a las variables obesidad (OBESIDAD) y la condición de asma (ASMA) como predictores. Exponencie los coeficientes de la regresión para obtener los OR.