6 Análisis exploratorio de datos (AED)
6.1 Paquetes y data
Los paquetes que se utilizarán son los siguientes:
La base ratones.csv contiene los datos del estudio (experimentos) de Winzell y Ahrén (2004) sobre un modelo animal (ratones) para estudiar los mecanismos y el tratamiento de la tolerancia a la glucosa alterada y la diabetes tipo 2 (Modificado de Data Analysis for the Life Sciences ).
ratones <- read_csv("data/ratones.csv")6.2 Medidas de frecuencia
6.2.1 Una variable
El paquete janitor (Firke 2021) tiene la función tabyl(), que permite generar tablas de frecuencias y se integra en el ecosistema de tidyverse.
tabyl() permite almacenar el objeto del cálculo de frecuencias en formato tidy para su manipulación posterior.
| Diet | n | percent |
|---|---|---|
| chow | 449 | 0.5307329 |
| hf | 397 | 0.4692671 |
Adicionalmente, podemos configurar nuestra tabla con adorn_*(). Por ejemplo, podemos utilizar adorn_totals("row") para agregar el total de las filas y adorn_pct_formatting() para dar formato a la columna de porcentajes.
ratones %>%
tabyl(Diet) %>%
adorn_totals("row") %>%
adorn_pct_formatting() Diet n percent
chow 449 53.1%
hf 397 46.9%
Total 846 100.0%6.2.2 Tabulaciones cruzadas
Podemos realizar tablas de doble entrada (frecuencias de 2 variables) con tabyl():
Al igual que con las frecuencias de una variable, podemos cambiar el formato de la tabla con adorn_*(). Se puede encontrar más información detallada de las opciones de formato en la viñeta de tabyls.
ratones %>%
tabyl(Diet, Sex) %>%
adorn_percentages("col") %>%
adorn_pct_formatting(digits = 2) %>%
adorn_ns() Diet F M
chow 52.94% (225) 53.21% (224)
hf 47.06% (200) 46.79% (197)Otro paquete con funciones útiles para medidas descriptivas es pubh (Athens 2022), el cual está enfocado en salud pública. La función cross_tbl() permite realizar también tablas de doble entrada.
|
F, N = 425 |
M, N = 421 |
Overall, N = 846 |
|
|---|---|---|---|
| Diet | |||
| chow | 225 (53%) | 224 (53%) | 449 (53%) |
| hf | 200 (47%) | 197 (47%) | 397 (47%) |
Se puede generar tablas de frecuencias con múltiples variables categóricas.
6.3 Medidas de tendencia central
6.3.1 Media aritmética
Con la función mean() calculamos la media aritmética o promedio de una variable, dada por la ecuación
donde \(n\) es el número de datos en la muestra.
Por ejemplo, para la variable glucose:
mean(ratones$glucose)[1] 7.006728O de forma alternativa usando tidyverse
6.3.2 Mediana
A diferencia de la media, la mediana nos permite identificar el valor que divide una distribución de datos ordenados por la mitad:
\[\begin{equation} \mathrm{mediana}\left(x\right) = \begin{cases} x\left[\frac{n}{2}\right] & \text{si $n$ es par} \\ \frac{x\left[\frac{n-1}{2}\right] + x\left[\frac{n+1}{2}\right]}{2} & \text{si $n$ es impar} \end{cases} \end{equation}\]donde \(n\) es el número de datos y \([\) \(]\) denota el número de orden de los datos ordenados.
La función median() nos permite calcular la mediana de una variable. Por ejemplo, con la variable glucose:
median(ratones$glucose)[1] 7.00021O de forma alternativa usando tidyverse
6.3.3 Moda
La moda nos da como resultado el valor más frecuente en la muestra. Suele ser utilizado para variables categóricas.
R no tiene una función base para calcular la moda. Utilizaremos la función Mode() del paquete pracma (Borchers 2022).
Mode(ratones$glucose)[1] 7.029131O de forma alternativa usando tidyverse
6.4 Medidas de dispersión
6.4.1 Rango
Se conoce como rango a la diferencia entre el valor máximo y el mínimo observados. También se le llama amplitud total o recorrido.
\[\begin{equation} \mathrm{rango}\left(x\right) = \mathrm{max}\left(x\right) - \mathrm{min}\left(x\right) \end{equation}\]Podemos utilizar las funciones max() y min() para hallar el valor mínimo y máximo de una variable, respectivamente, y luego calcular su rango:
maximo <- max(ratones$glucose)
maximo[1] 8.315831minimo <- min(ratones$glucose)
minimo[1] 5.65037rango <- maximo - minimo
rango[1] 2.665461Para hallar el rango como intervalo, podemos utilizar la función range(). Comprobamos que el resultado sea igual al de max() y min().
range(ratones$glucose)[1] 5.650370 8.315831O de forma alternativa usando tidyverse
6.4.2 Rango intercuartil (RIC)
Con la función IQR() hallamos el rango intercuartil, el cual es la diferencia entre los percentiles 75 (cuartil 3) y el percentil 25 (cuartil 1):
Usando glucose:
IQR(ratones$glucose)[1] 0.5067847O de forma alternativa usando tidyverse
6.4.3 Desviación estándar
Con la desviación estándar, calculamos la desviación promedio de los datos con respecto a su media:
\[\begin{equation} s\left(x\right) = \sqrt{\frac{\sum_{i=1}^{n}{\left(x_{i}-\bar{x}\right)}}{n-1}} \end{equation}\]donde \(n\) es el número de datos en la muestra.
En R, podemos usar la función sd():
sd(ratones$glucose)[1] 0.383118O de forma alternativa usando tidyverse
6.4.4 Varianza muestral
También podemos utilizar la función var() para obtener la varianza muestral, la cual es la desviación estándar al cuadrado, \(\mathrm{var}\left(x\right) = s^{2}\).
var(ratones$glucose)[1] 0.1467794O de forma alternativa usando tidyverse
6.4.5 Coeficiente de variación
El coeficiente de variación mide la variabilidad relativa a la media de los datos. Dado que el coeficiente de variación no tiene una unidad de medida, se puede usar para comparar variables con diferentes escalas de medición. La fórmula del coeficiente de variación es la siguiente:
\[\begin{equation} \mathrm{cv}\left(x\right) = \frac{\sigma}{\bar{x}} \end{equation}\]En R, podemos crear fácilmente una función para calcular el coeficiente de variación:
Usando glucose, tenemos:
cv(ratones$glucose)[1] 0.05467859O de forma alternativa usando tidyverse
6.5 Medidas de localización y forma
Para explicar y entender mejor la distribución de los datos de una variable, utilizamos las medidas de asimetría (skewness) y curtosis (kurtosis).
6.5.1 Asimetría
La asimetría nos indica qué tanto y en qué dirección la distribución de los datos es asimétrica con respecto a su media. Se toma como referencia la distribución normal, la cual es idealmente simétrica, para evaluar la asimetría de una distribución.
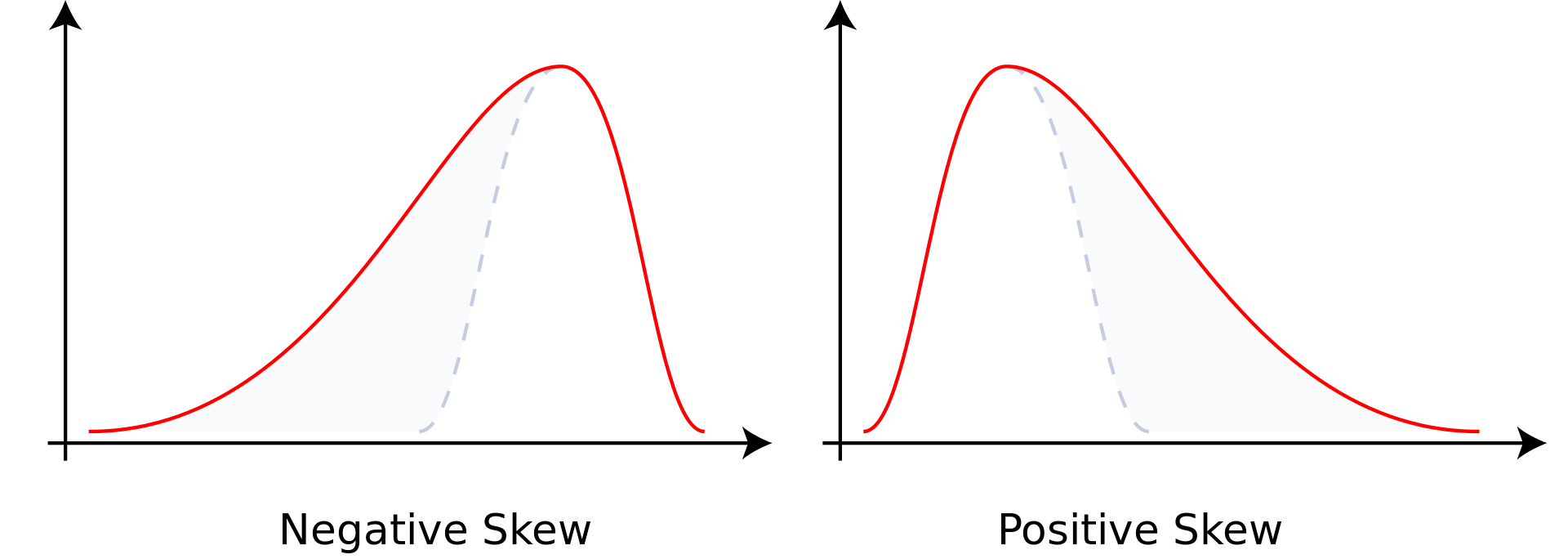
Una asimetría negativa nos dice que la zona con mayor densidad de la distribución está hacia la derecha, y por tanto la distribución posee una cola a la izquierda, mientras que una asimetría positiva nos dice que la zona con mayor densidad de la distribución está hacia la izquierda y que posee una cola hacia la derecha.
Veamos cómo se ve la distribución de la variable glucose mediante un histograma.
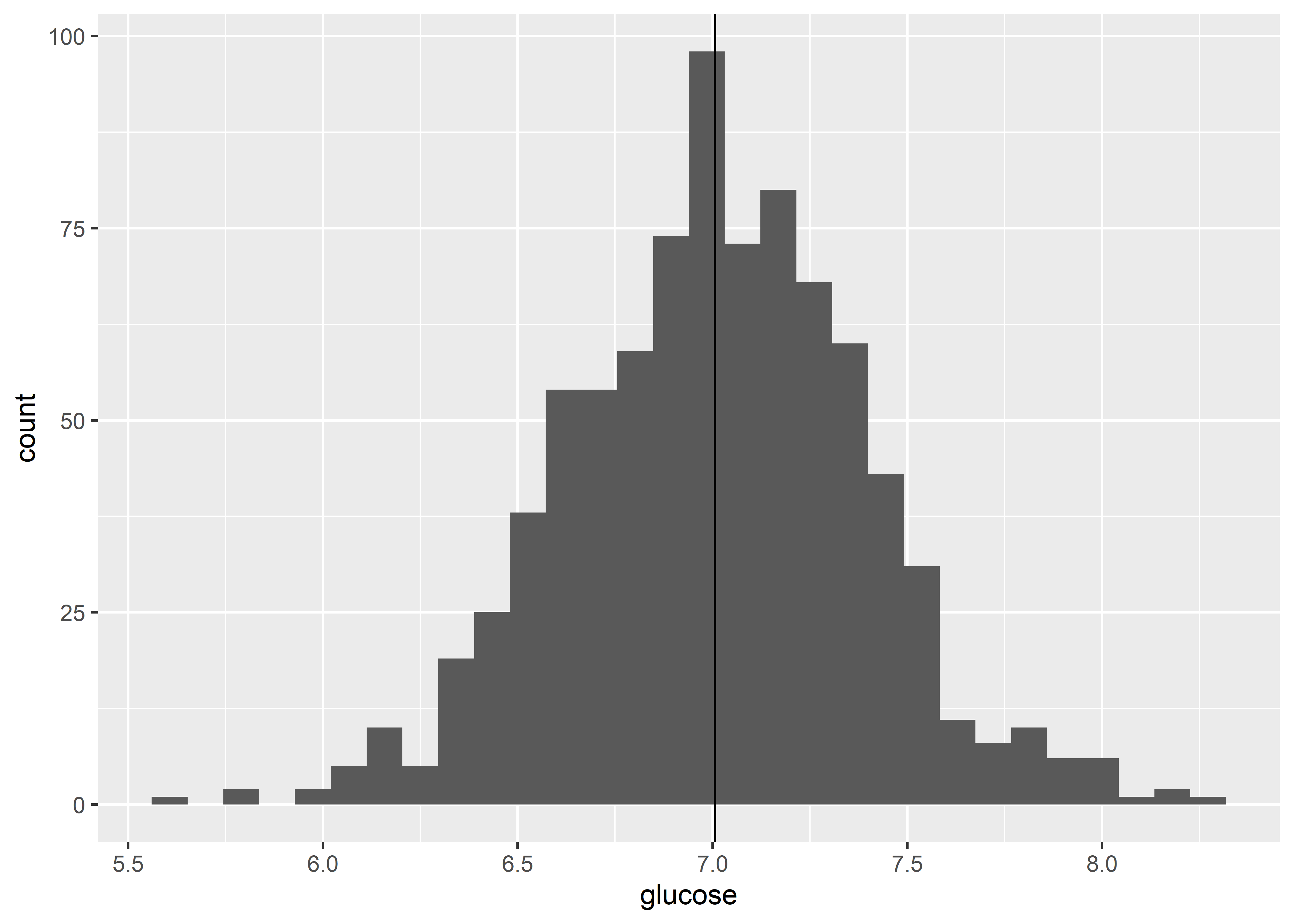
En la figura anterior, la línea vertical representa a la media de la distribución. A simple vista, la distribución no parece ser asimétrica. Para comprobarlo, podemos usar la función skewness() del paquete moments (Komsta y Novomestky 2022) para calcular la asimetría.
skewness(ratones$glucose)[1] 0.001214676O de forma alternativa usando tidyverse
Debido a que el valor obtenido es muy pequeño, podemos asumir que la distribución de esta variable no presenta asimetría.
6.5.2 Curtosis
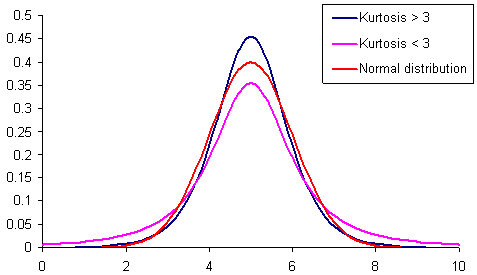
La curtosis es una medida de qué tan “pesadas” son las colas de una distribución; es decir, cuánta densidad de probabilidad contienen. Al igual que la asimetría, la curtosis se calcula relativamente a la distribución normal, la cual tiene una curtosis de 3. Una curtosis alta en magnitud indica que hay valores muy extremos, mientras que una curtosis pequeña indica que no hay valores muy extremos.
Por otro lado, una curtosis positiva quiere decir que la distribución tiene las colas más pesadas que la distribución normal, mientras que una curtosis negativa quiere decir que la distribución tiene colas menos pesadas que la distribución normal.
La curtosis es calculada con la función kurtosis() del paquete moments.
kurtosis(ratones$glucose)[1] 3.355597O de forma alternativa usando tidyverse
En este caso, el valor de la curtosis se encuentra muy cercano al valor ideal de 3. Esto quiere decir que la distribución tiene colas muy similares en densidad a las de la distribución normal.
6.5.3 Prueba de Jarque-Bera
De forma alternativa, el paquete moments ofrece una función para el cálculo de la prueba de Jarque-Bera. Esta es una prueba de bondad de ajuste cuya hipótesis nula es que el conjunto de datos tiene una asimetría (skewness) y curtosis que coincide con una distribución normal.
jarque.test(ratones$glucose)
Jarque-Bera Normality Test
data: ratones$glucose
JB = 4.4575, p-value = 0.1077
alternative hypothesis: greaterSegún esta prueba, no tenemos evidencia suficiente para decir que esta variable tiene una asimetría y curtosis diferente de una distribución normal.
Sin embargo, como toda prueba estadística, es sensible al tamaño de la muestra y por tanto se sugiere no basarse unicamente en la prueba de hipótesis para tomar una desición sobre la distribución de nuestra variable.
6.6 Múltiples métricas
Con la función summary(), obtenemos un resumen de las principales medidas de una variable (valor mínimo, 1er cuartil, mediana (2do cuartil), media, 3er cuartil y valor máximo):
summary(ratones$glucose) Min. 1st Qu. Median Mean 3rd Qu. Max.
5.650 6.744 7.000 7.007 7.251 8.316 Podemos usar la función estat() del paquete pubh para obtener múltiples medidas de tendencia central en formato tidy:
La función skim() del paquete skimr también provee una exploración de métricas para variables categóricas y continuas.
| Name | Piped data |
| Number of rows | 846 |
| Number of columns | 10 |
| _______________________ | |
| Column type frequency: | |
| character | 3 |
| numeric | 7 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| Sex | 0 | 1 | 1 | 1 | 0 | 2 | 0 |
| Diet | 0 | 1 | 2 | 4 | 0 | 2 | 0 |
| gen_w | 0 | 1 | 8 | 8 | 0 | 2 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| Bodyweight | 5 | 0.99 | 28.85 | 6.26 | 15.51 | 24.04 | 28.19 | 32.95 | 54.08 | ▃▇▅▁▁ |
| glucose | 0 | 1.00 | 7.01 | 0.38 | 5.65 | 6.74 | 7.00 | 7.25 | 8.32 | ▁▃▇▃▁ |
| en_intake | 0 | 1.00 | 43.07 | 3.97 | 36.88 | 39.80 | 42.40 | 45.43 | 56.20 | ▇▇▅▂▁ |
| insulin | 0 | 1.00 | 497.12 | 110.45 | 80.88 | 425.85 | 494.07 | 567.83 | 964.36 | ▁▃▇▂▁ |
| meta_eff | 0 | 1.00 | 547.78 | 123.09 | 307.74 | 444.71 | 546.88 | 649.90 | 792.26 | ▅▇▇▇▅ |
| ein_resp | 0 | 1.00 | 5002.99 | 191.30 | 4078.18 | 4894.64 | 5023.54 | 5131.30 | 5471.18 | ▁▁▃▇▂ |
| time | 0 | 1.00 | 720.23 | 5.59 | 703.52 | 716.37 | 720.40 | 723.75 | 739.74 | ▁▅▇▃▁ |
La función cross_tbl() del paquete pubh permite mostrar medidas descriptivas de variables categóricas y continuas.
ratones %>%
cross_tbl(by = "Sex") %>%
theme_pubh()|
F, N = 425 |
M, N = 421 |
Overall, N = 846 |
|
|---|---|---|---|
| Diet | |||
| chow | 225 (53%) | 224 (53%) | 449 (53%) |
| hf | 200 (47%) | 197 (47%) | 397 (47%) |
| Bodyweight | 24.5 (22.1, 27.5) | 32.3 (29.1, 36.3) | 28.2 (24.0, 33.0) |
| Unknown | 0 | 5 | 5 |
| glucose | 6.99 (6.74, 7.24) | 7.00 (6.76, 7.26) | 7.00 (6.74, 7.25) |
| en_intake | 42.2 (39.8, 45.2) | 42.5 (39.8, 45.8) | 42.4 (39.8, 45.4) |
| insulin | 495 (426, 567) | 494 (428, 569) | 494 (426, 568) |
| meta_eff | 554 (454, 649) | 539 (440, 652) | 547 (445, 650) |
| ein_resp | 5,023 (4,880, 5,135) | 5,024 (4,910, 5,126) | 5,024 (4,895, 5,131) |
| time | 720.1 (716.3, 723.8) | 720.6 (716.5, 723.7) | 720.4 (716.4, 723.8) |
| gen_w | |||
| negative | 412 (97%) | 354 (84%) | 766 (91%) |
| positive | 13 (3.1%) | 67 (16%) | 80 (9.5%) |
Otros paquetes que se pueden explorar para múltiples métricas son
infer,desctable,psychyHmisc. Se puede encontrar una lista más completa en el post de Adam Medcalf.
6.7 Métricas estratificadas
Con la función summaryBy() del paquete doBy (Højsgaard y Halekoh 2022), podemos comparar múltiples métricas estratificadas por una segunda variable.
En el código a continuación, compararemos la variable glucosa (glucose) en función de diagnóstico molecular (gen_w). Utilizando los datos del objeto ratones, calcularemos la media (mean), desviación estándar (sd), mediana (median), tamaño (length), simetría (skewness) y curtosis (kurtosis)
En algunas ocasiones, debemos utilizar la función
as.data.framepara cambiar el formato del objeto del conjunto de datos:ratones <- as.data.frame(ratones)
summaryBy(
glucose ~ gen_w, data = ratones, FUN = c(mean, sd, median, skewness, kurtosis),
na.rm = T
)# A tibble: 2 × 6
gen_w glucose.mean glucose.sd glucose.median glucose.skewness glucose.kurtosis
<chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 nega… 7.02 0.384 7.01 0.0245 3.38
2 posi… 6.92 0.367 6.95 -0.320 2.84Podemos realizar la misma rutina con la función stat() del paquete pubh dentro del ecosistema tidyverse.
Es importante notar que la variable sobre la cual vamos a estratificar nuestras métricas tiene que estar en formato
factor. Para cambiar una variable a tipo de dato factor, podemos usar la funciónas.factor().
gen_w N Min Max Mean Median SD CV
1 glucose negative 766 5.65 8.32 7.02 7.01 0.38 0.05
2 positive 80 5.83 7.60 6.92 6.95 0.37 0.05También se puede estratificar usando la función group_by() del paquete dplyr y la función skim() del paquete skimr:
| Name | Piped data |
| Number of rows | 846 |
| Number of columns | 2 |
| _______________________ | |
| Column type frequency: | |
| numeric | 1 |
| ________________________ | |
| Group variables | gen_w |
Variable type: numeric
| skim_variable | gen_w | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|---|
| glucose | negative | 0 | 1 | 7.02 | 0.38 | 5.65 | 6.77 | 7.01 | 7.25 | 8.32 | ▁▃▇▃▁ |
| glucose | positive | 0 | 1 | 6.92 | 0.37 | 5.83 | 6.67 | 6.95 | 7.16 | 7.60 | ▁▂▆▇▅ |
6.8 Tablas descriptivas con gtsummary
El paquete gtsummary permite crear tablas descriptivas o de resumen con formato de publicación de manera sencilla. La función principal de este paquete es tbl_summary(). El comportamiento por defecto de esta función es resumir todas las variables de un conjunto de datos que se le pase y mostrar estadísticas de resumen según el tipo de variable (categórica o continua).
Por ejemplo, con el conjunto de datos ratones:
library(gtsummary)
tbl_summary(ratones)| Characteristic | N = 8461 |
|---|---|
| Sex | |
| F | 425 (50%) |
| M | 421 (50%) |
| Diet | |
| chow | 449 (53%) |
| hf | 397 (47%) |
| Bodyweight | 28.2 (24.0, 33.0) |
| Unknown | 5 |
| glucose | 7.00 (6.74, 7.25) |
| en_intake | 42.4 (39.8, 45.4) |
| insulin | 494 (426, 568) |
| meta_eff | 547 (445, 650) |
| ein_resp | 5,024 (4,895, 5,131) |
| time | 720.4 (716.4, 723.8) |
| gen_w | |
| negative | 766 (91%) |
| positive | 80 (9.5%) |
| 1 n (%); Median (IQR) | |
Para las variables categóricas, esta función calcula por defecto el número de observaciones por categoría y el porcentaje de las observaciones sobre el total. Por otro lado, para las variables continuas, la función calcula por defecto la mediana y el intervalo del 50% central de la distribución de las observaciones; es decir, el intervalo comprendido entre el percentil 25 y el percentil 75. Además, en presencia de valores ausentes para una variable, la función agrega el conteo de NAs bajo la etiqueta Unknown.
Para hacer una selección de las variables que queremos resumir, podemos usar el parámetro include:
tbl_summary(ratones, include = c(Diet, glucose, insulin))| Characteristic | N = 8461 |
|---|---|
| Diet | |
| chow | 449 (53%) |
| hf | 397 (47%) |
| glucose | 7.00 (6.74, 7.25) |
| insulin | 494 (426, 568) |
| 1 n (%); Median (IQR) | |
Podemos estraficar por alguna variable categórica usando el parámetro by. Por ejemplo, describamos las variables glucose y insulin por tipo de dieta:
tbl_summary(ratones, include = c(Diet, glucose, insulin), by = Diet)| Characteristic | chow, N = 4491 | hf, N = 3971 |
|---|---|---|
| glucose | 7.03 (6.76, 7.27) | 6.98 (6.73, 7.24) |
| insulin | 499 (434, 568) | 491 (422, 569) |
| 1 Median (IQR) | ||
Si quisieramos cambiar las estadísticas descriptivas que se calculan, podemos usar el parámetro statistic. Para especificar las variables y sus estadísticas descriptivas con este parámetro, se usa la notación de fórmula. En R, la sintaxis de una fórmula está dada por y ~ x, la cual se lee como y en función de x. En el caso de las tablas descriptivas, en el lado izquierdo de la fórmula especificamos la(s) variable(s) y en el lado derecho especificamos cómo queremos mostrar la(s) estadística(s) descriptiva(s) que queremos calcular. El formato lo especificamos en una cadena, poniendo las estadísticas entre llaves.
Por ejemplo, el formato por defecto para el resumen de las variables continuas es "{median} ({p25}, {p75})". Si quisiéramos calcular la media y la desviación estándar, el formato podría ser "{mean} ({sd})". Generalmente, los nombres de las estadísticas se asemejan a las funciones de R para calcularlas. Para mayor información sobre la notación de estos formatos ver ?tbl_summary().
Por otro lado, para especificar las variables en la fórmula de statistic, podemos usar las funciones de ayuda all_categorical() y all_continuous() para seleccionar todas las variables categóricas y continuas, respectivamente. Por ejemplo, calculemos la media y la desviación estándar de las variables glucose y insulin por tipo de dieta:
ratones |>
tbl_summary(
include = c(Diet, glucose, insulin),
by = Diet,
statistic = all_continuous() ~ "{mean} ({sd})"
)| Characteristic | chow, N = 4491 | hf, N = 3971 |
|---|---|---|
| glucose | 7.03 (0.39) | 6.98 (0.37) |
| insulin | 500 (110) | 494 (111) |
| 1 Mean (SD) | ||
Si, por ejemplo, quisiéramos calcular el máximo y el mínimo (rango) de estas variables, el formato podría ser el siguiente:
ratones |>
tbl_summary(
include = c(Diet, glucose, insulin),
by = Diet,
statistic = all_continuous() ~ "({min}, {max})"
)| Characteristic | chow, N = 4491 | hf, N = 3971 |
|---|---|---|
| glucose | (5.65, 8.21) | (5.82, 8.32) |
| insulin | (81, 964) | (81, 823) |
| 1 (Range) | ||
También podemos calcular estadísticas para las variables continuas en múltiples líneas. Para esto, tenemos que usar el parámetro type para decirle a la función que todas las variables continuas sean del tipo "continuous2" usando también la notación de fórmula. Además, en el parámetro statistic tenemos que agregar en un vector con todos los resúmenes descriptivos que queremos hacer. Por ejemplo:
ratones |>
tbl_summary(
include = c(Diet, glucose, insulin),
by = Diet,
type = all_continuous() ~ "continuous2",
statistic = all_continuous() ~ c(
"{mean} ({sd})", "{median} ({p25}, {p75})", "({min}, {max})"
)
)| Characteristic | chow, N = 449 | hf, N = 397 |
|---|---|---|
| glucose | ||
| Mean (SD) | 7.03 (0.39) | 6.98 (0.37) |
| Median (IQR) | 7.03 (6.76, 7.27) | 6.98 (6.73, 7.24) |
| (Range) | (5.65, 8.21) | (5.82, 8.32) |
| insulin | ||
| Mean (SD) | 500 (110) | 494 (111) |
| Median (IQR) | 499 (434, 568) | 491 (422, 569) |
| (Range) | (81, 964) | (81, 823) |
El paquete gtsummary tiene un gran número de herramientas para generar y personalizar tablas. En este capítulo, se ha mostrado solo la funcionalidad básica. En los siguientes capítulos se hará uso de este paquete y se mostrarán funcionalidades adicionales. Para mayor detalle sobre las funcionalidades, además de tutoriales, visitar la página web del paquete en gtsummary.
6.9 Visualización y AED
6.9.1 Análisis de una variable
6.9.1.1 Frecuencias
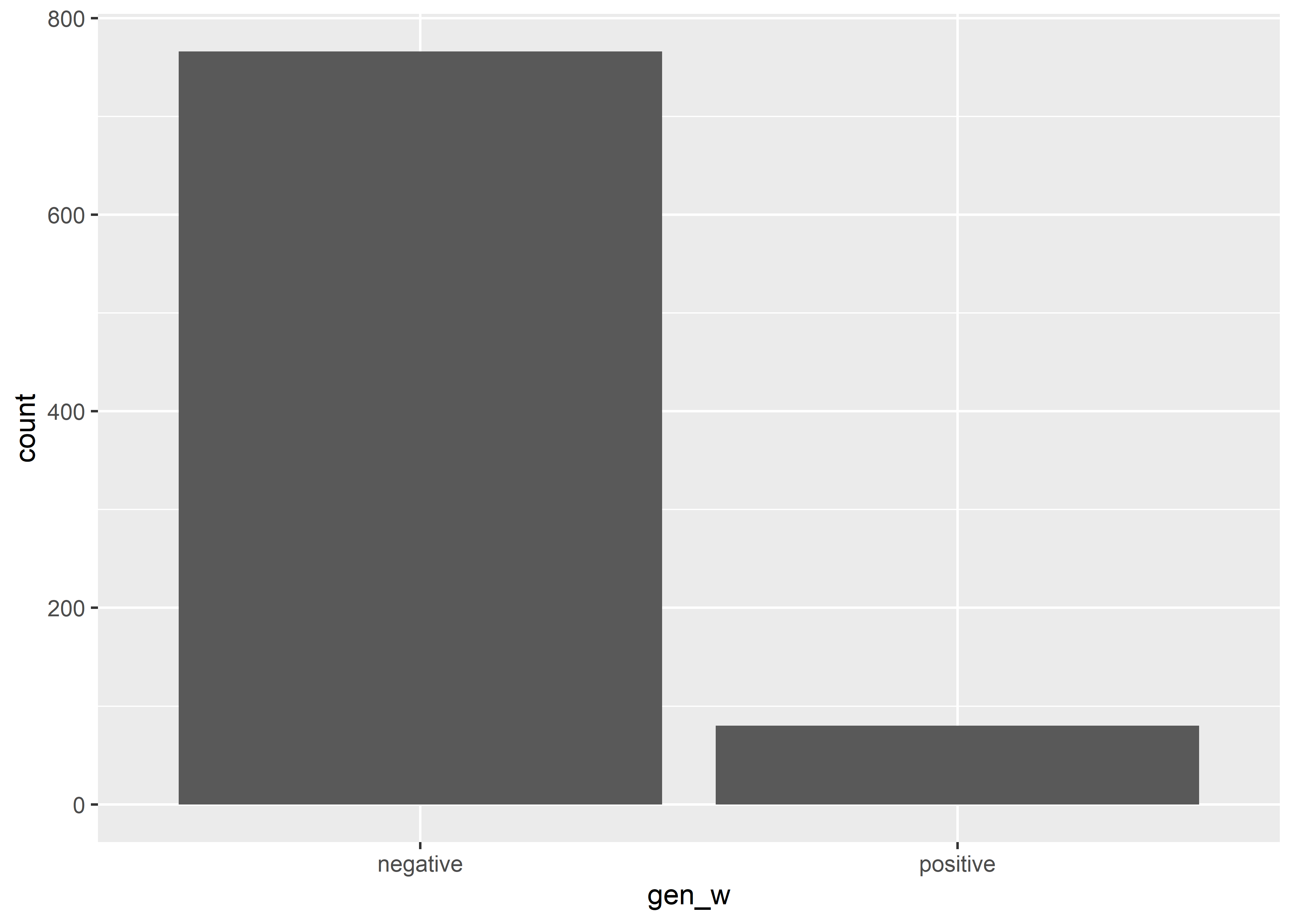
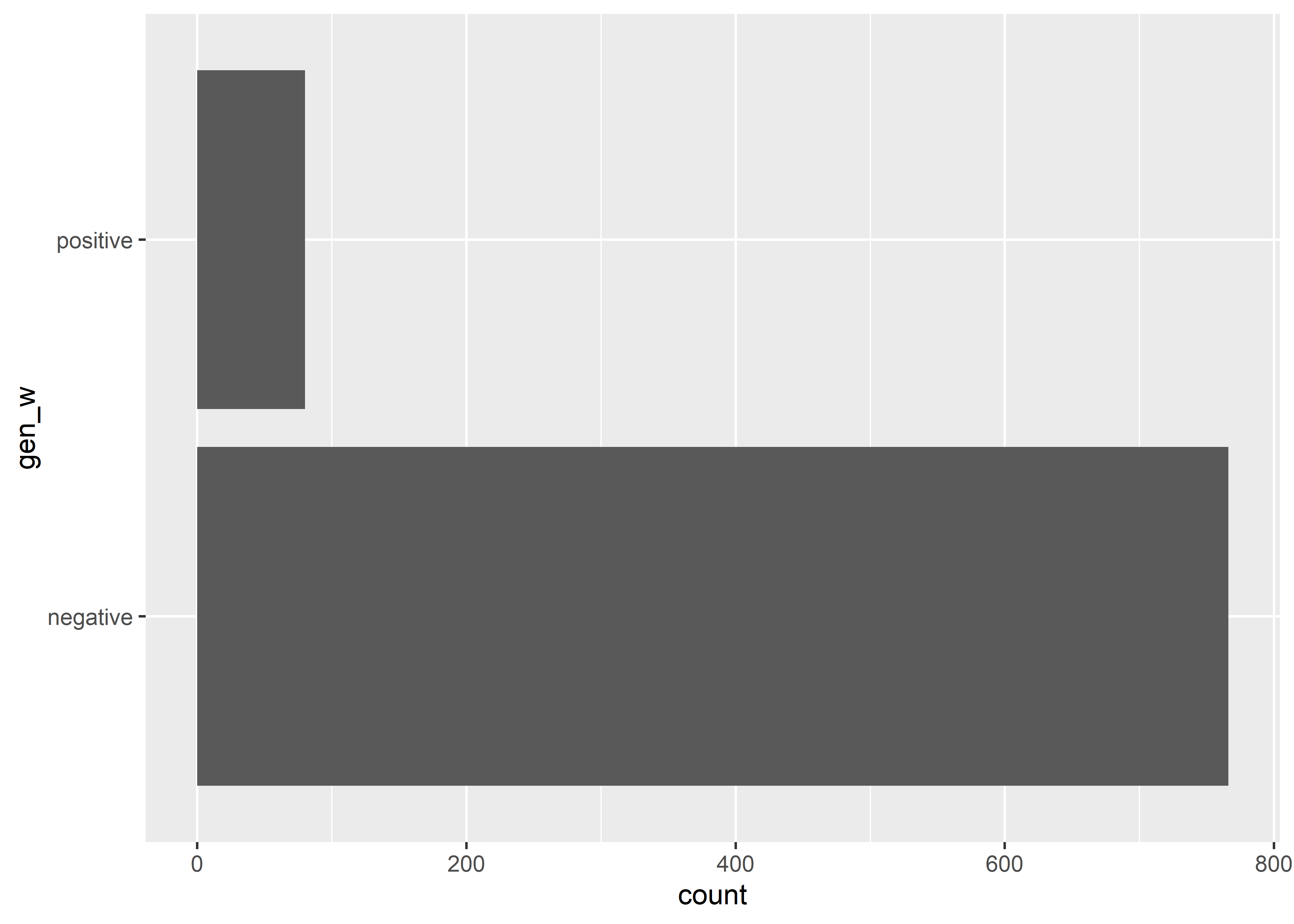
La geometría geom_bar() permite visualizar las frecuencias de una sola variable. En el siguiente ejemplo visualizaremos la distribución de los resultados de las pruebas genéticas.
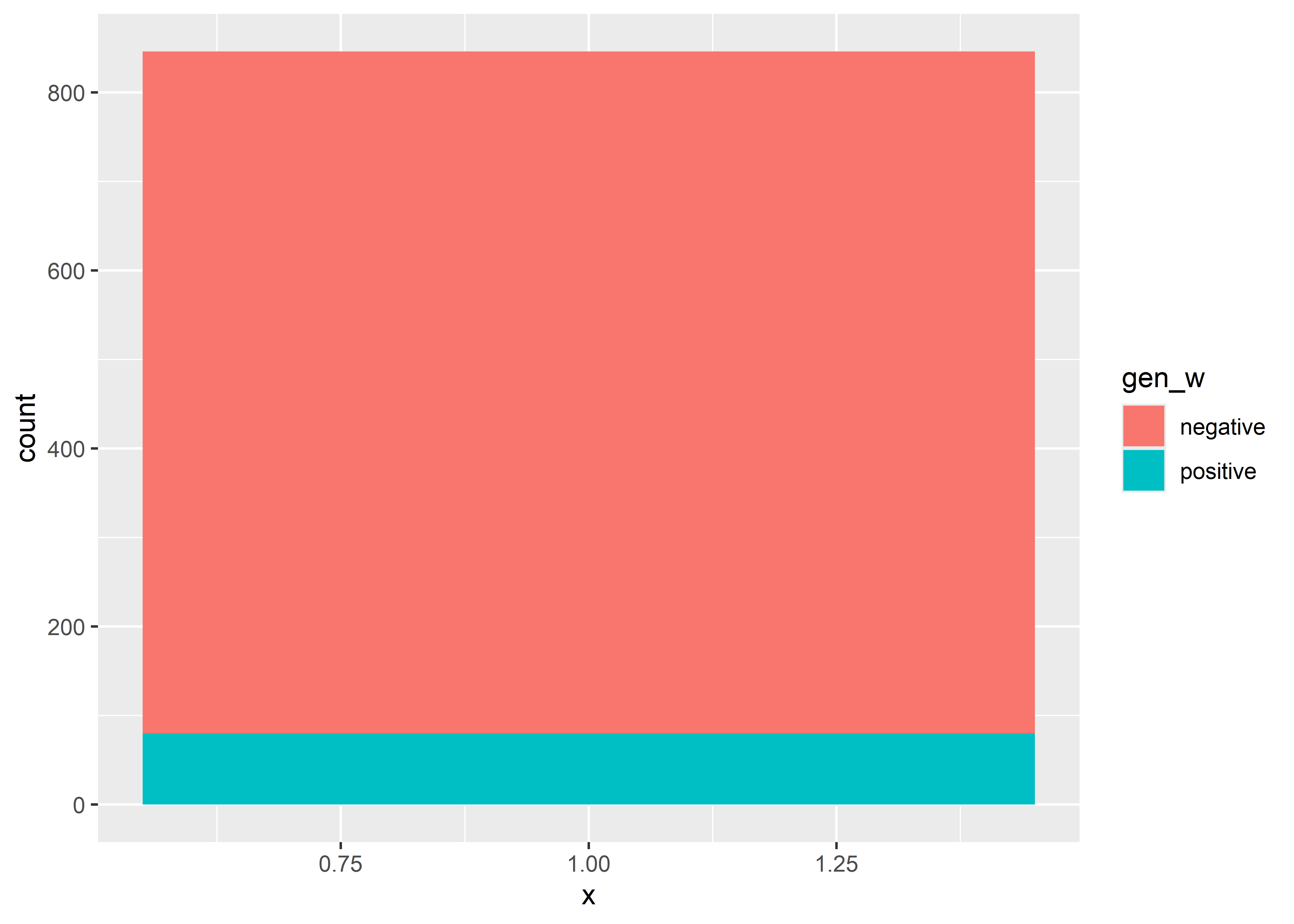
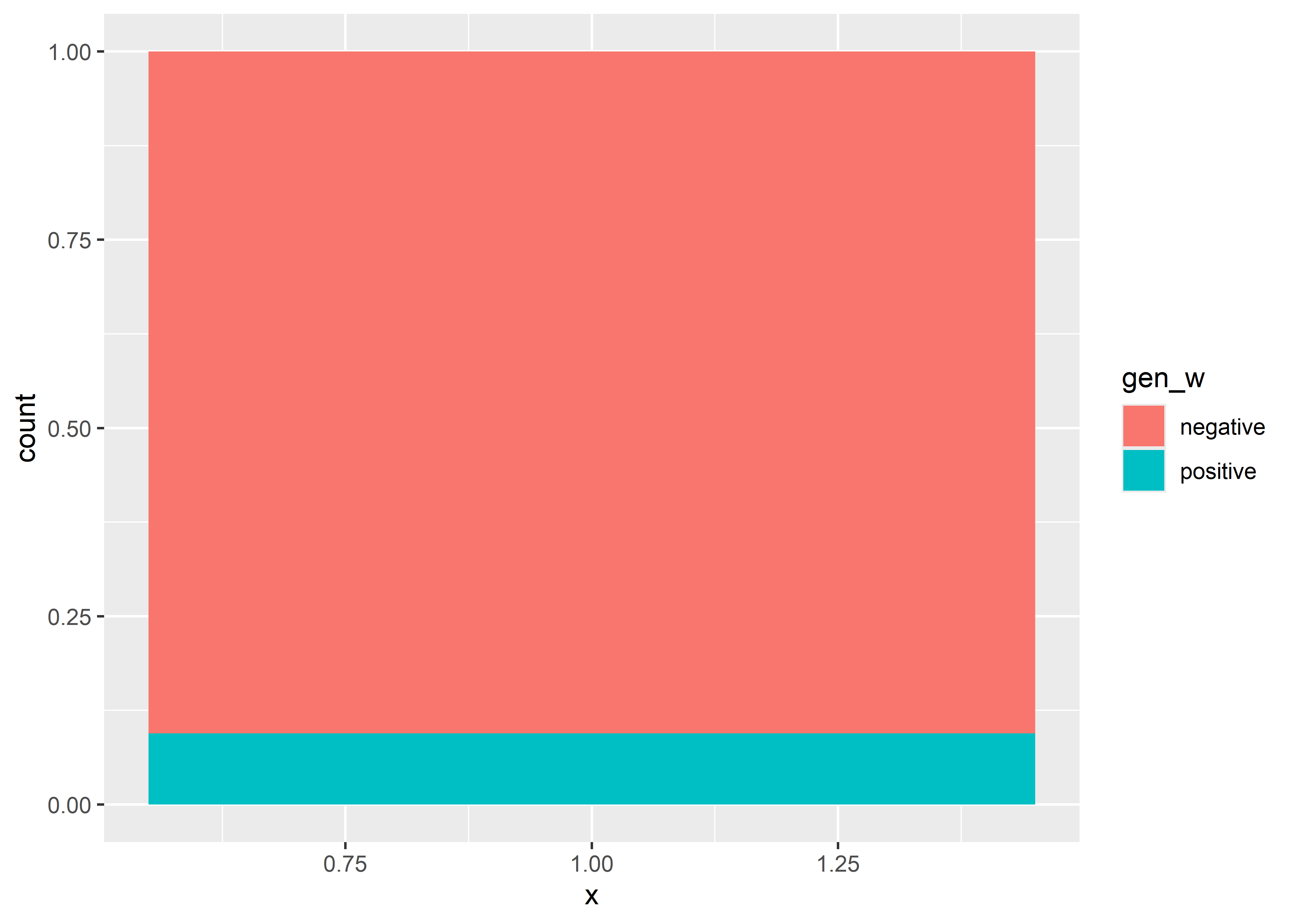
También podemos visualizar estos datos de forma apilada
Y podemos visualizar estos datos de forma relativa cambiando el argumento postion dentro de geom_bar().
Si cambiamos el sistema de coordenadas de nuestro gráfico a polar podemos obtener un gráfico de Pie
ratones %>%
ggplot(aes(x = 1, fill=gen_w)) +
geom_bar(position = "fill") +
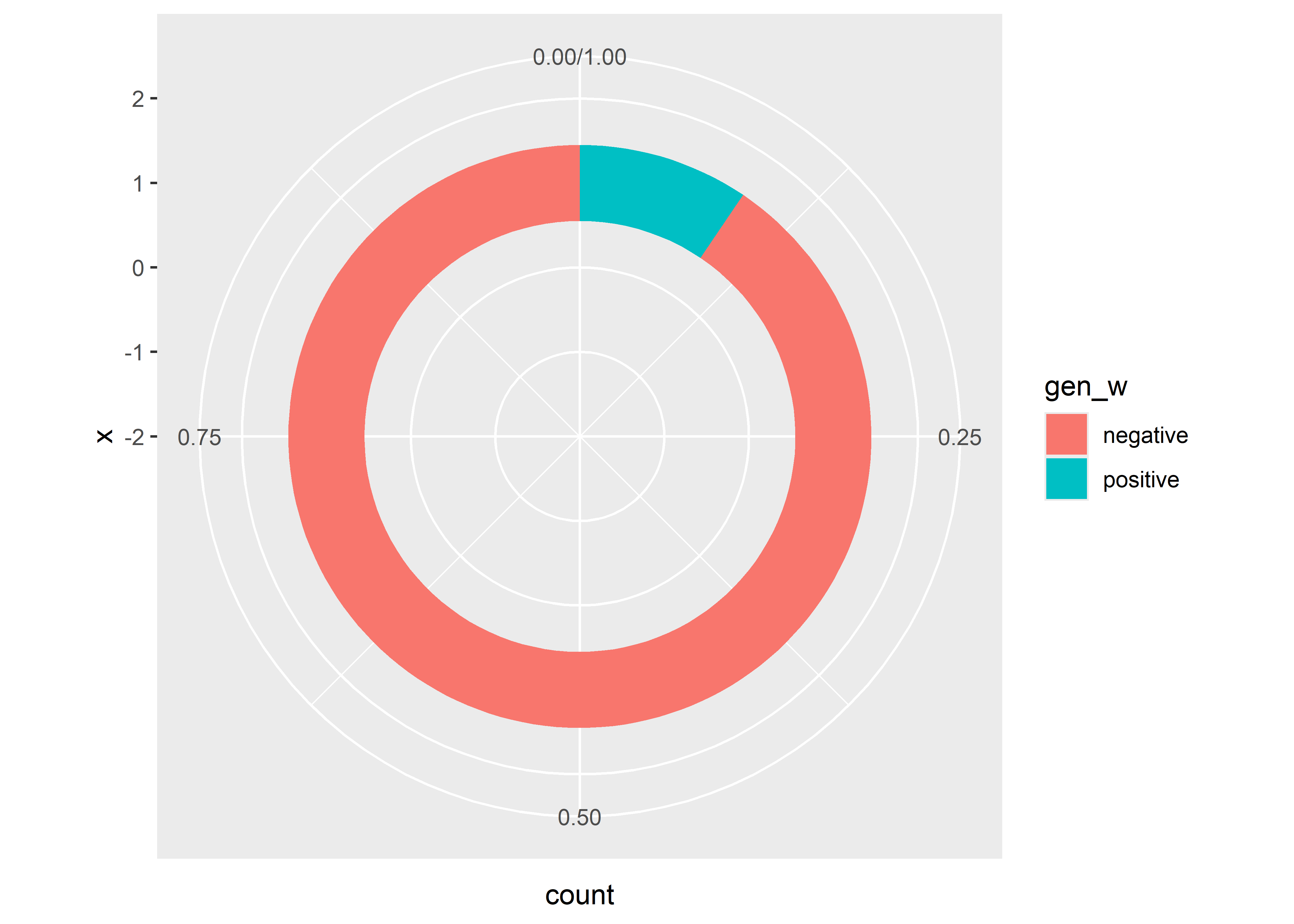
coord_polar(theta = "y")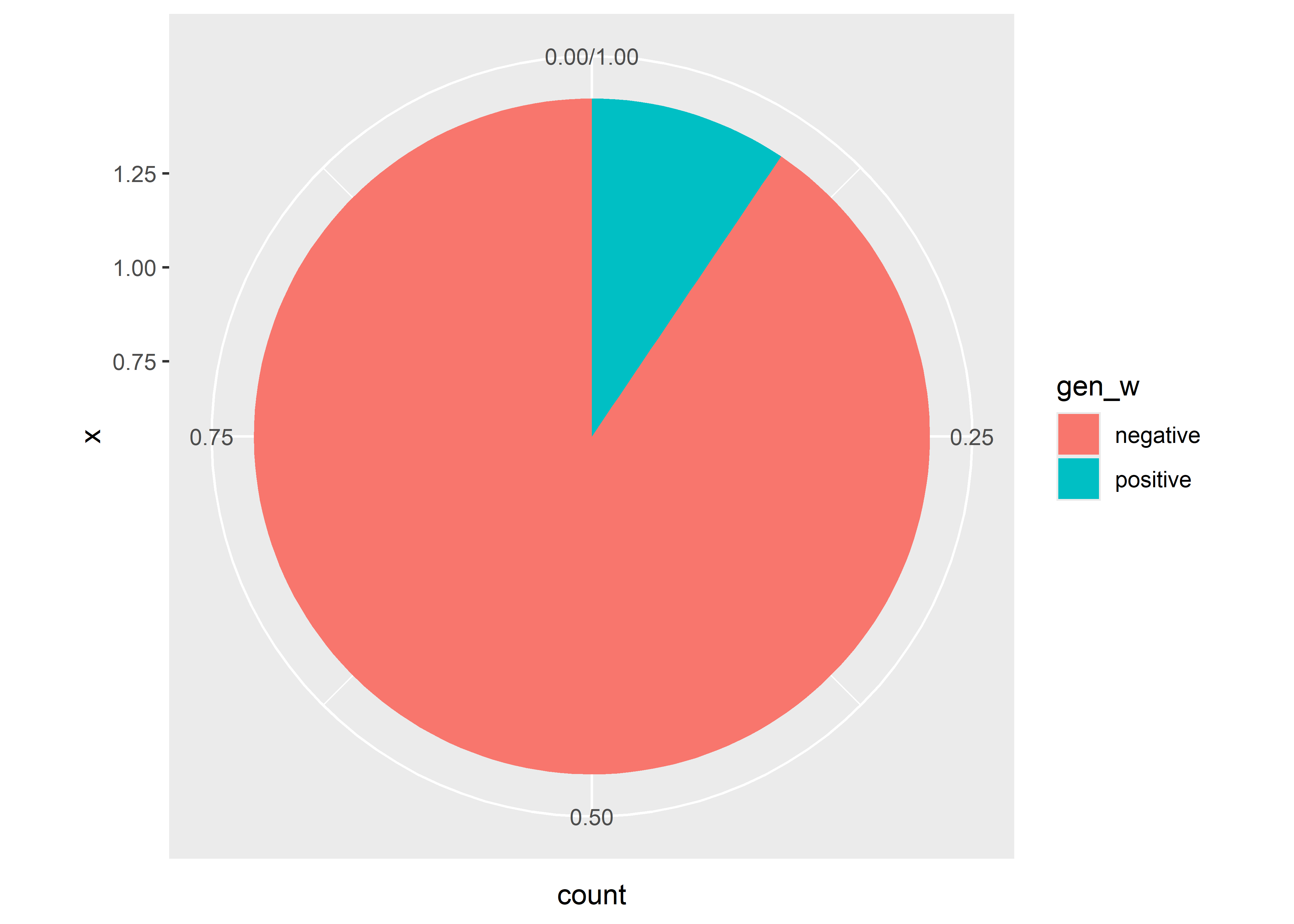
Este gráfico de Pie es muy popular pero no se recomienda dentro del AED principalmente por las dificultades en interpretar los ángulos y áreas como se explica es este post de from Data to Viz. Como alternativa podemos utilizar un gráfico tipo Donut.
6.9.1.2 Stem plot
Con la función stem() generamos un gráfico de texto, conocido como diagrama de tallos y hojas, el cual nos permite visualizar la distribución de un grupo de observaciones.
En este caso, utilizaremos la variable glucose.
stem(ratones$glucose)
The decimal point is 1 digit(s) to the left of the |
56 | 5
58 | 236
60 | 2246802245569
62 | 000134800111344567777888888
64 | 00002233334556666677788888889990011222333334444444555555666677777788
66 | 00000002222222233333344444444445555566677777888890000000000011111122+37
68 | 00000000111122222233333344444444555555566666667788888888889999999999+98
70 | 00000000001111222222223333333333344444444445555566666666667777777788+82
72 | 00000000000011111111222222222222333333334444444455555555555556666666+68
74 | 00111111111222223333333444455666777778888990000022223333455555667777
76 | 00122234788901236999
78 | 0112245781123689
80 | 12386
82 | 126.9.1.3 Histograma
Similar a la función stem(), la función hist() nos permite visualizar la distribución de una variable a través de un histograma.
Nuevamente, utilizaremos la variable glucose para la visualización:
hist(ratones$glucose)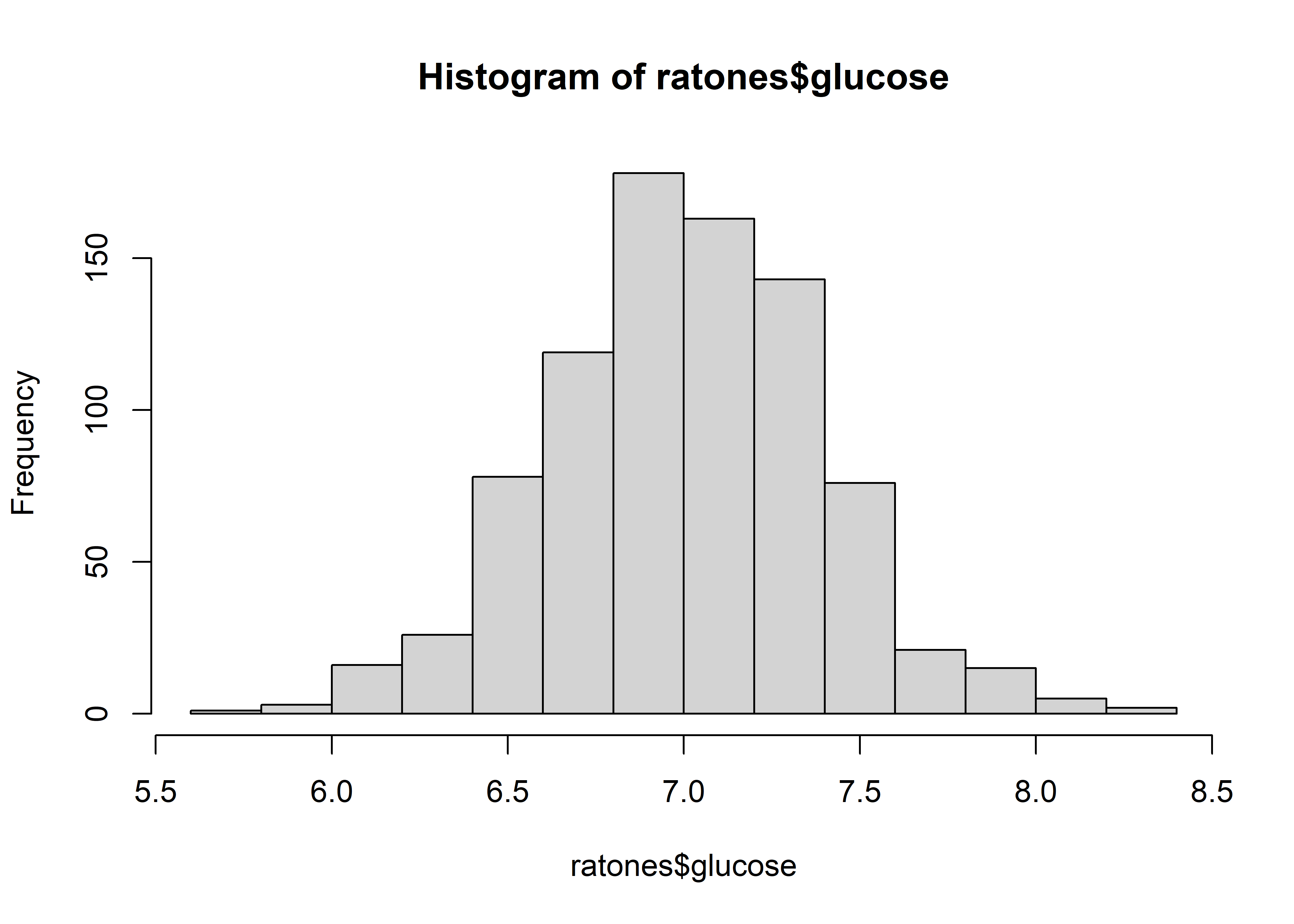
Podemos generar el mismo gráfico en el ecosistema tidyverse con ggplot y la geometría geom_histogram():
ratones %>%
ggplot(aes(x = glucose)) +
geom_histogram()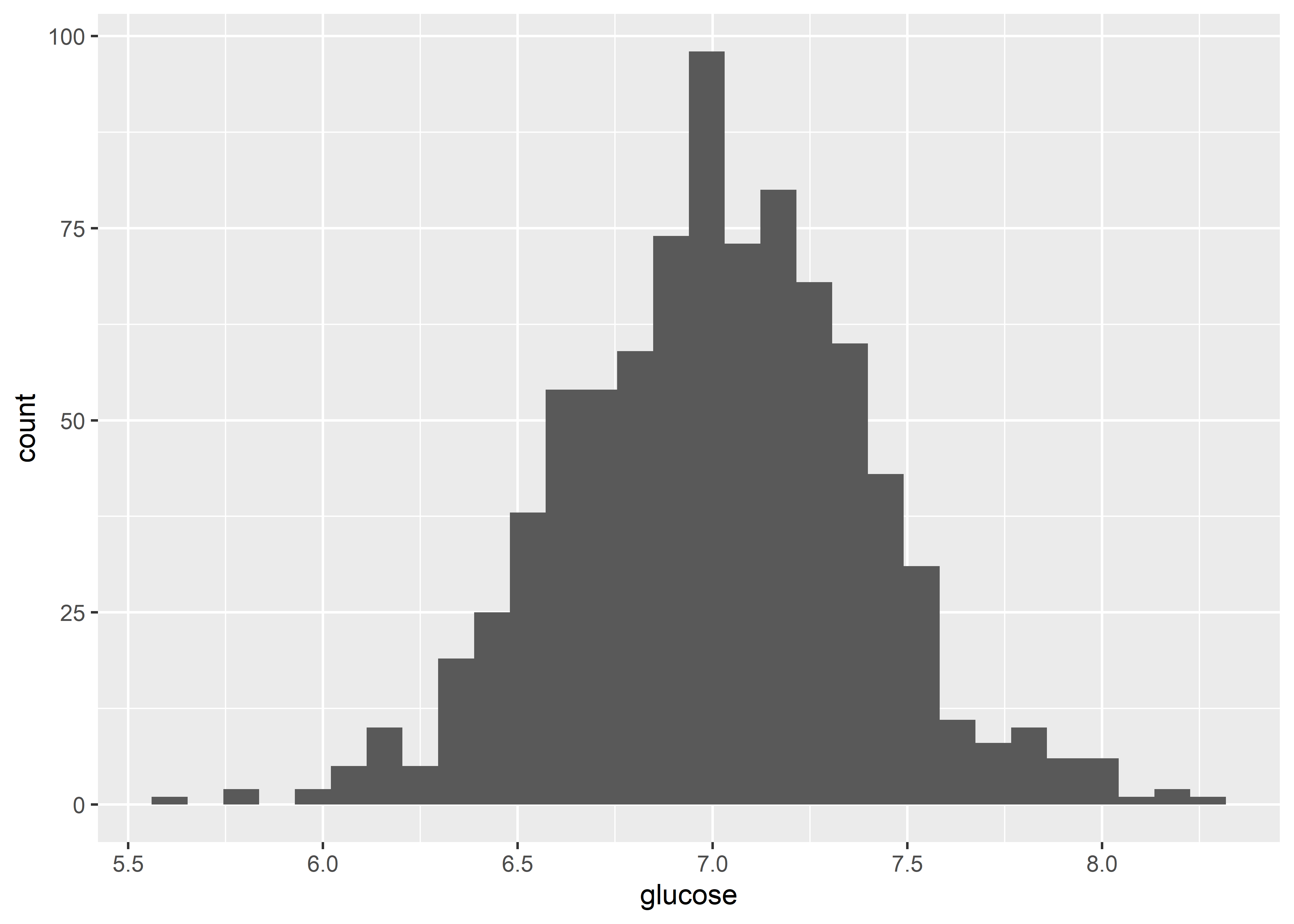
Anotaciones
Utilizaremos la flexibilidad gráfica de ggplot con la geometría geom_vline() para anotar nuestro histograma con las posiciones de nuestras tres medidas de tendencia central de la variable glucose:
- La media, de rojo
- La mediana, de azul
- La moda, de verde
ratones %>%
ggplot(aes(x = glucose)) +
geom_histogram() +
geom_vline(aes(xintercept = mean(glucose)), col = "red") +
geom_vline(aes(xintercept = median(glucose)), col = "blue") +
geom_vline(aes(xintercept = Mode(glucose)), col = "green")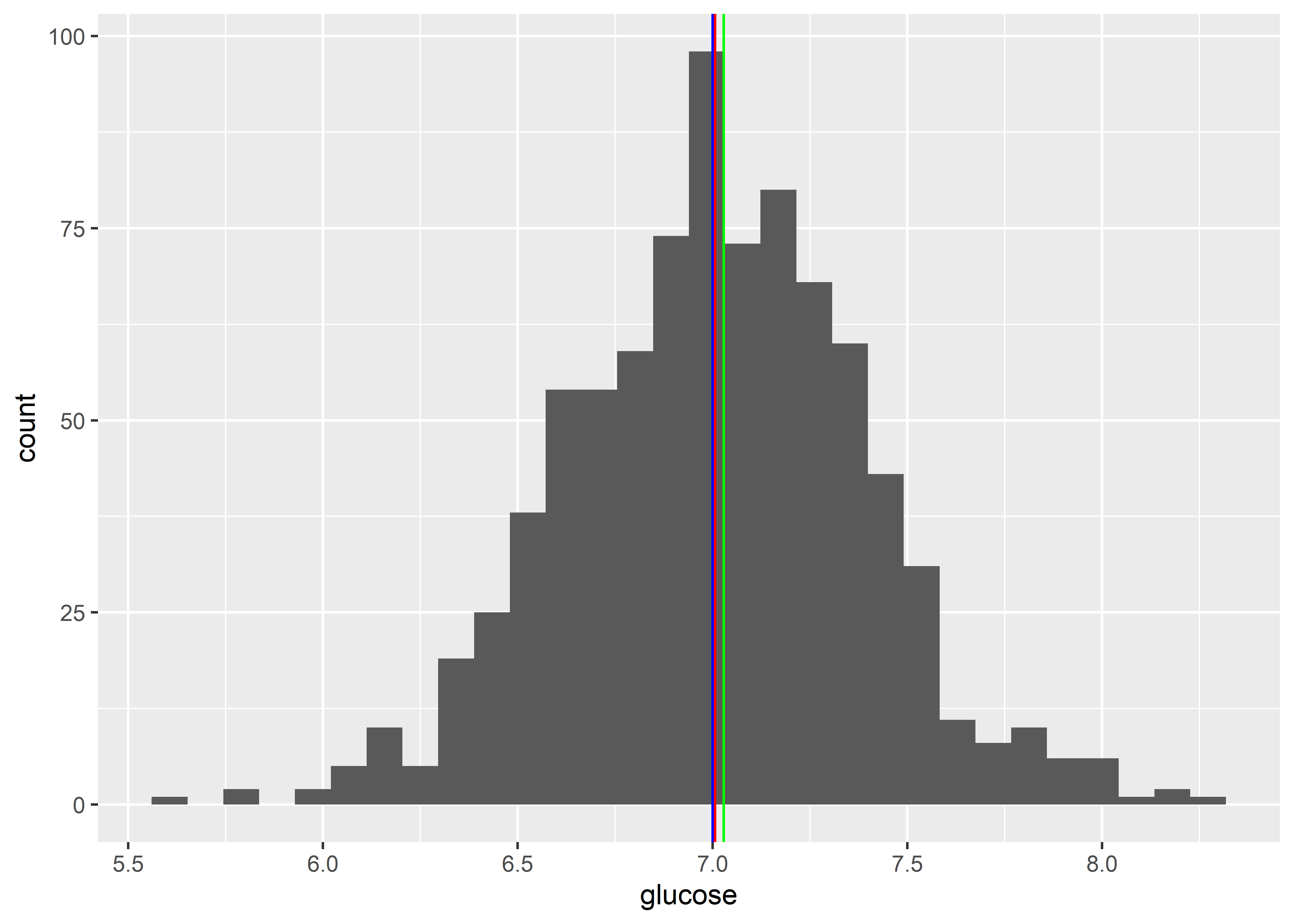
6.9.1.4 Boxplot
Usaremos la geometría geom_boxplot() para generar diagramas de caja (boxplots).
ratones %>%
ggplot(aes(x = glucose)) +
geom_boxplot()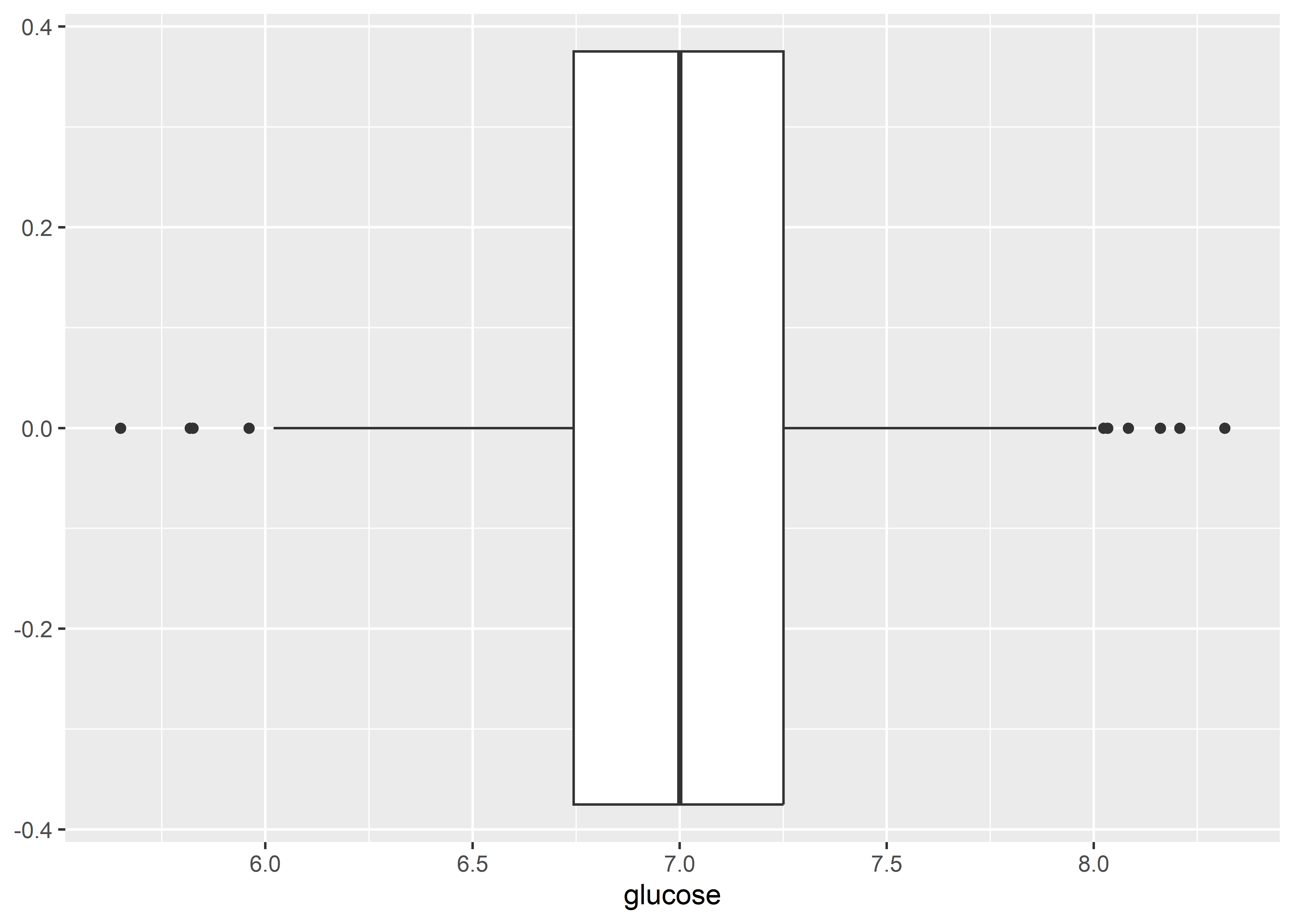
6.9.1.5 Gráficos estadísticos
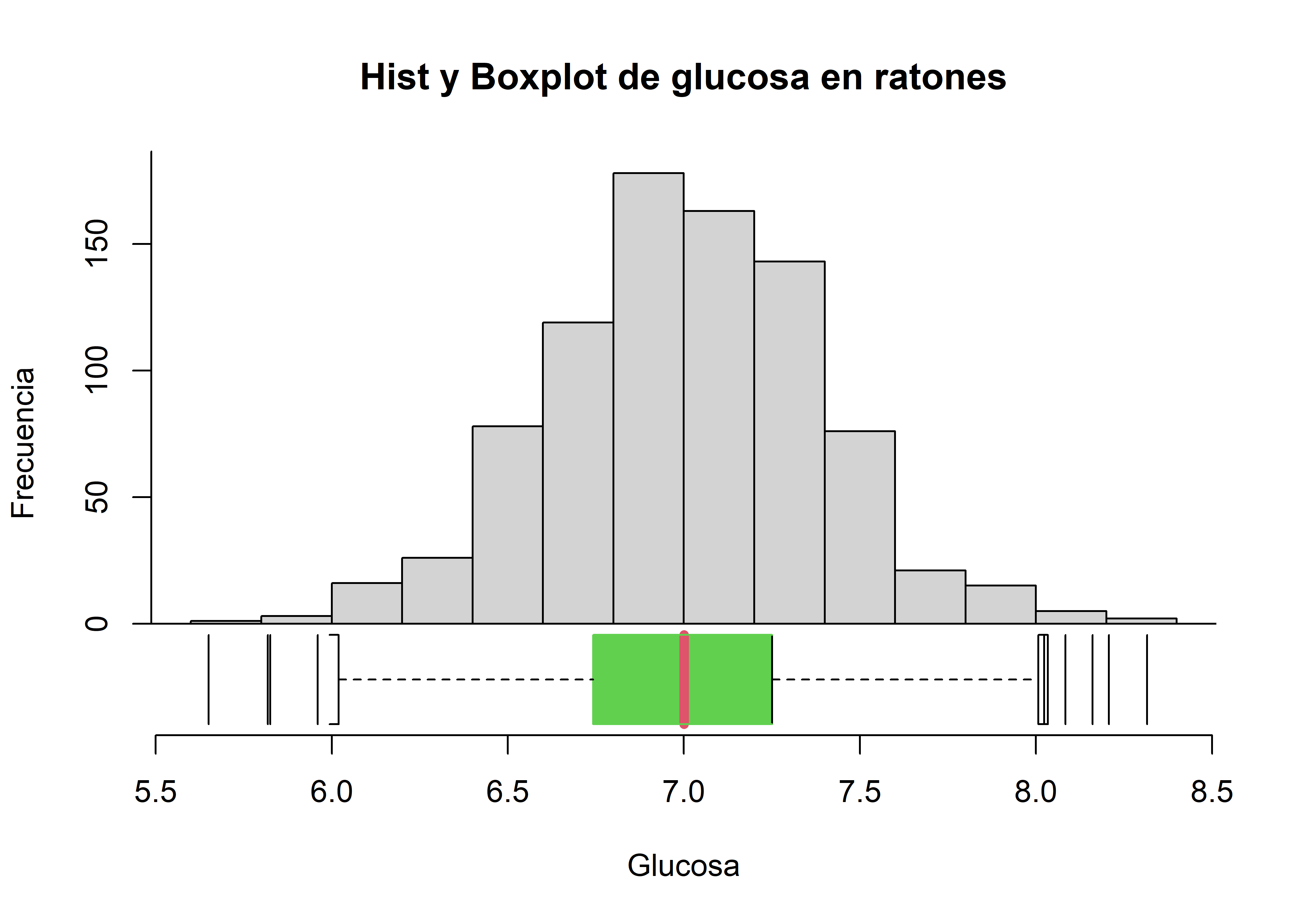
Podemos combinar múltiples gráficos para entender la información que proporciona cada gráfico. La función histBxp() del paquete sfsmisc (Maechler 2022) nos permite comparar el gráfico de histograma con el del boxplot.
histBxp(
ratones$glucose, main = "Hist y Boxplot de glucosa en ratones", xlab = "Glucosa",
ylab = "Frecuencia"
)
Con el paquete ggplot podemos combinar geometrías para lograr un gráfico equivalente.
ratones %>%
ggplot(aes(x = glucose)) +
geom_boxplot(width = 10) +
geom_histogram(fill = "transparent", col = "black")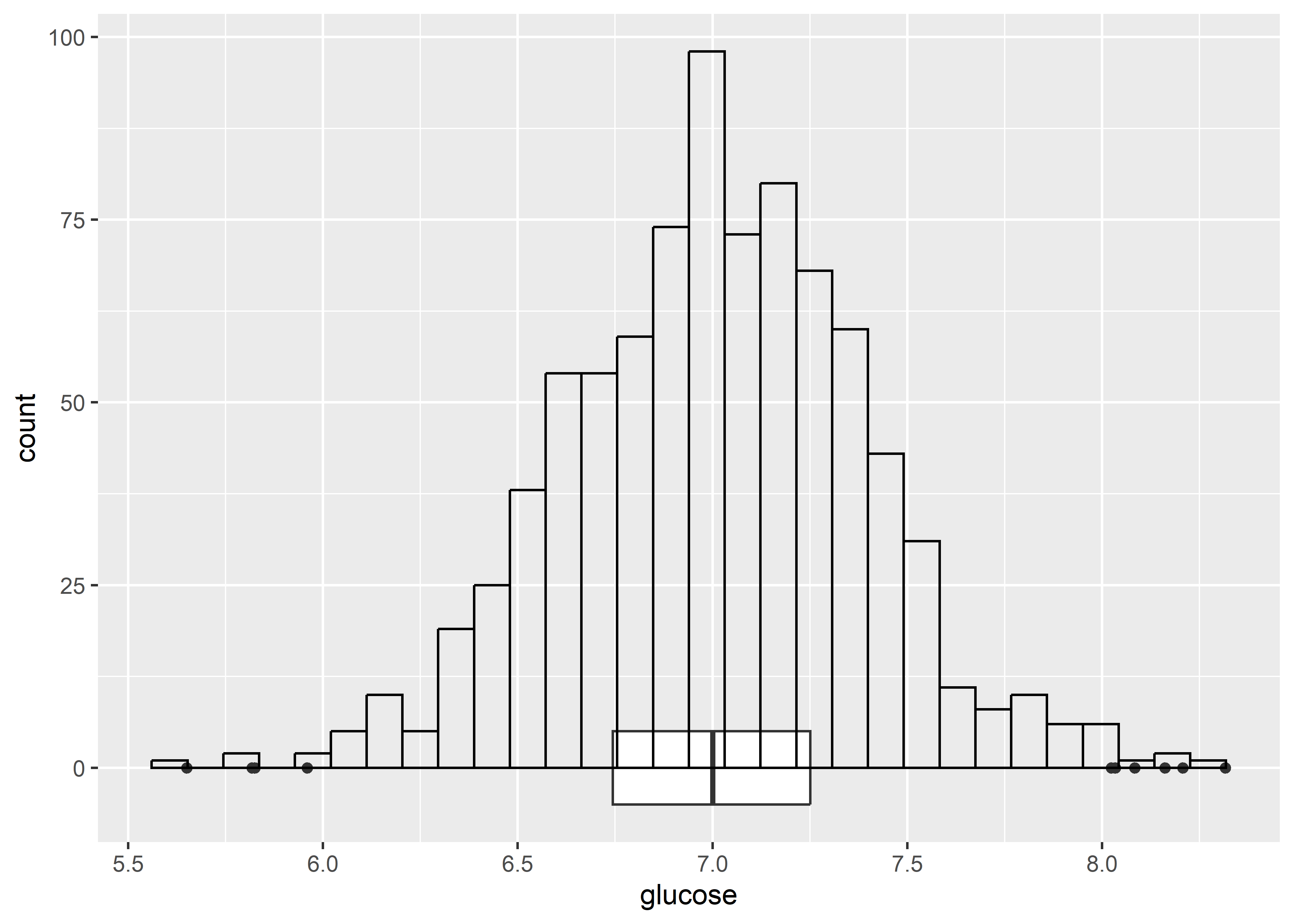
Adicionalmente, podemos agregar anotaciones de las posiciones de nuestras tres medidas de tendencia central de la variable glucose:
ratones %>%
ggplot(aes(x = glucose)) +
geom_boxplot(width = 10) +
geom_histogram(fill = "transparent", col = "black") +
geom_vline(aes(xintercept = mean(glucose)), col = "red") +
geom_vline(aes(xintercept = median(glucose)), col = "blue") +
geom_vline(aes(xintercept = Mode(glucose)), col = "green")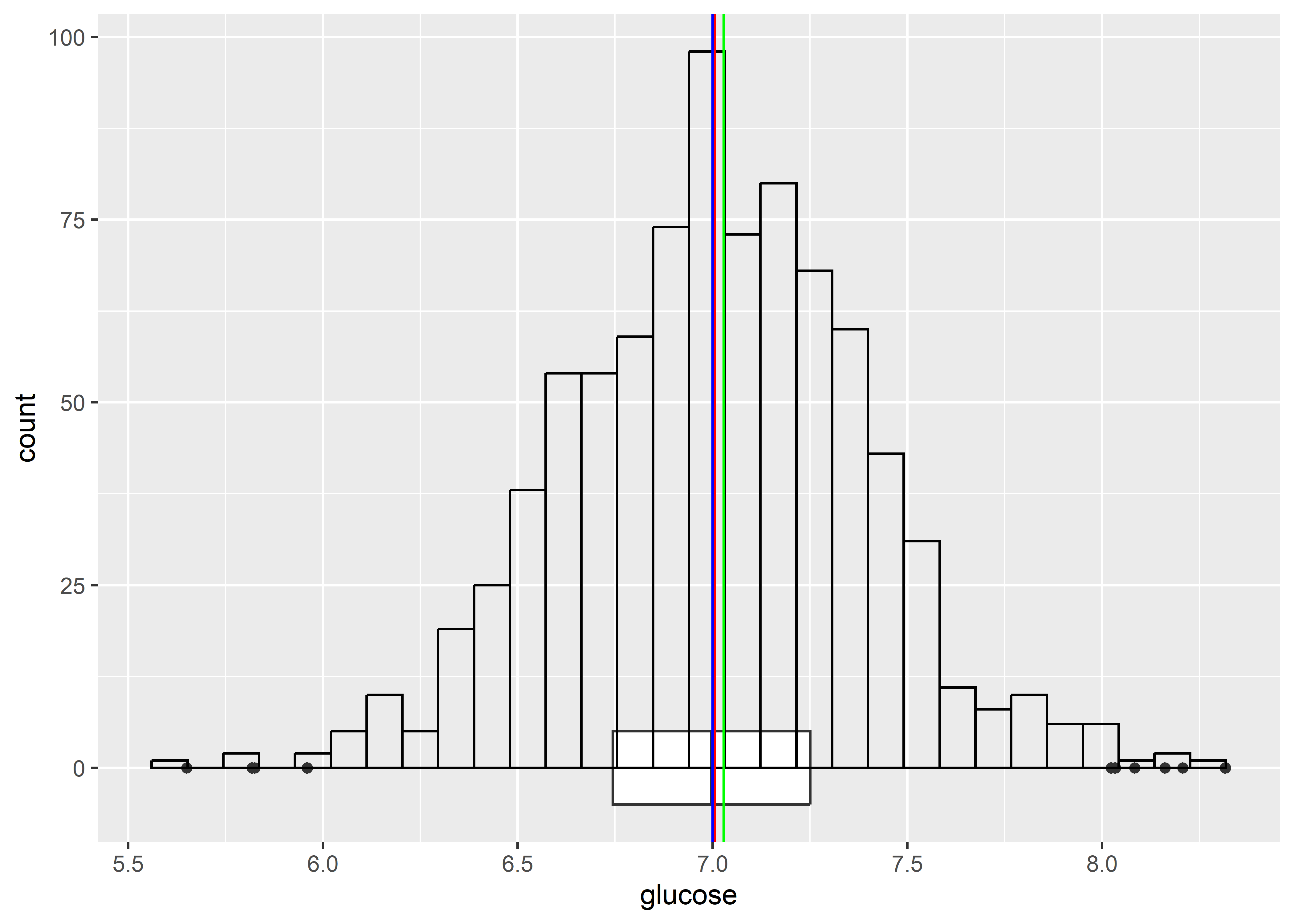
6.9.2 Comparación de dos variables
6.9.2.1 Categórica vs. categórica
Los gráficos de mosaicos nos permiten comparar dos variables categóricas. Usaremos la geometría geom_mosaic() del paquete ggmosaic (Jeppson, Hofmann, y Cook 2021)
ratones %>%
ggplot() +
geom_mosaic(aes(x = product(Sex, gen_w), fill = Sex))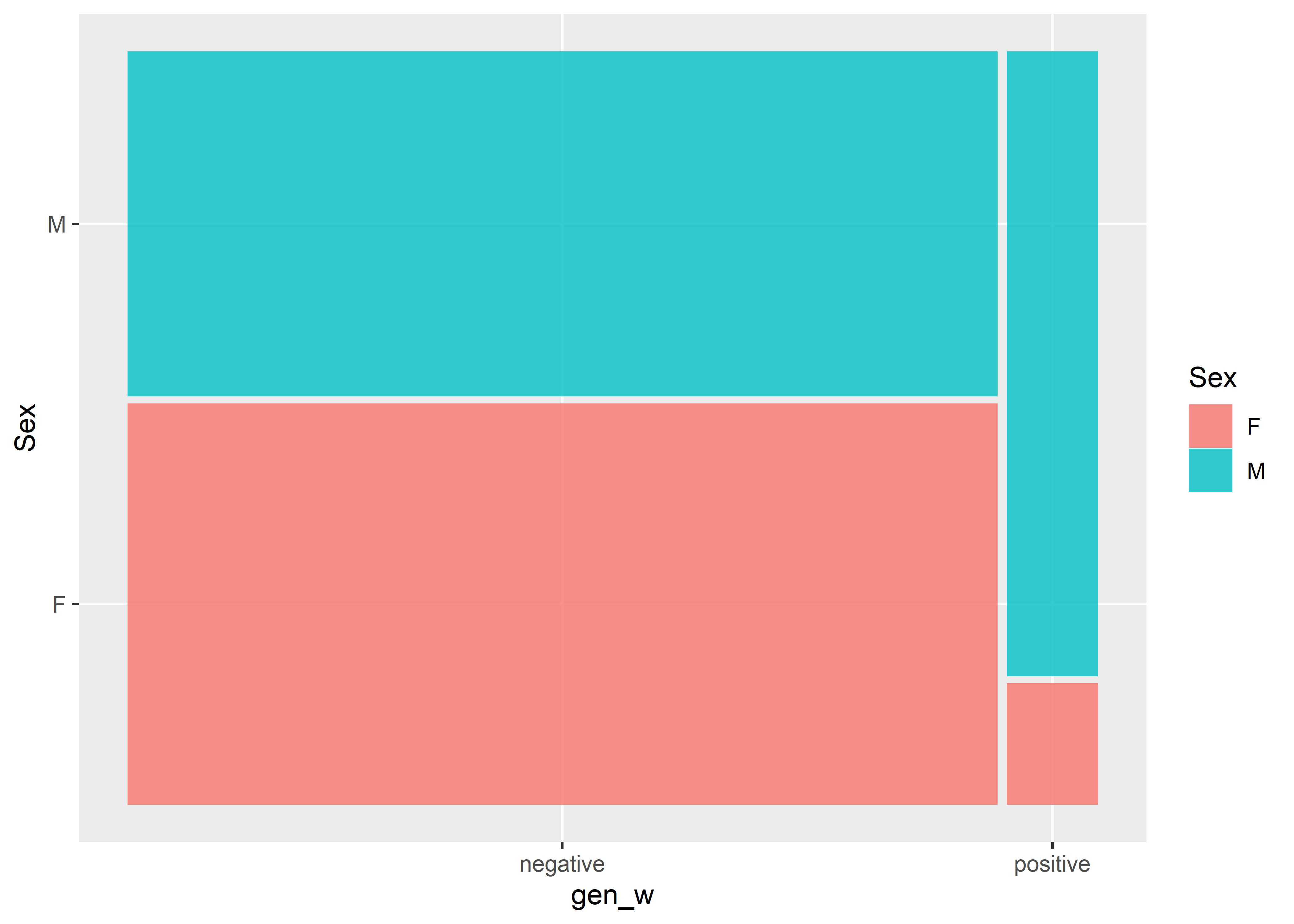
6.9.2.2 Continua vs. continua
Para comparar dos variables continuas en un gráfico de dispersión, utilizaremos la geometría geom_point() de ggplot.
Para el ejemplo, usaremos las variables ein_resp y time
ratones %>%
ggplot(aes(x = ein_resp, y = time)) +
geom_point() + geom_smooth()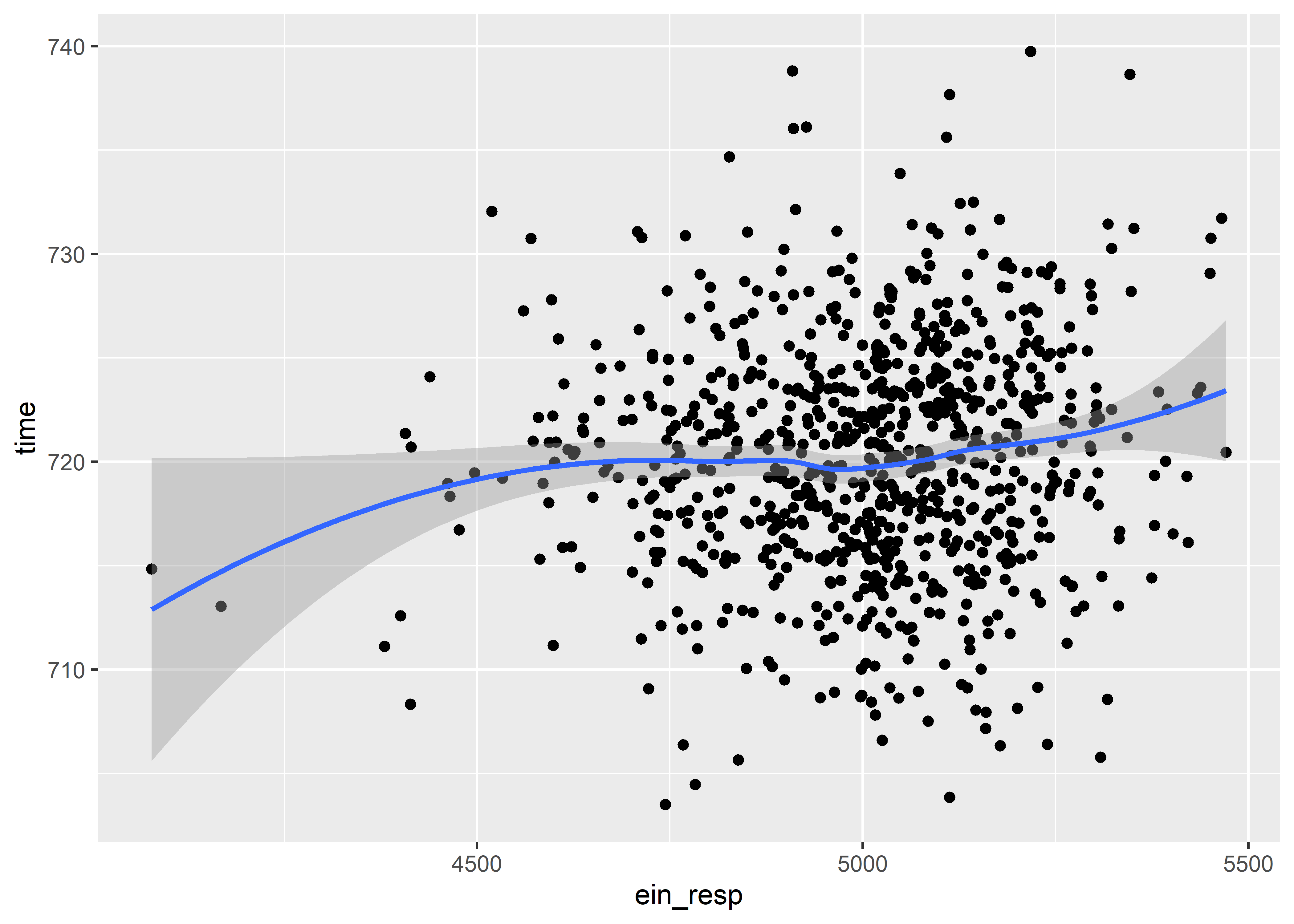
6.9.2.3 Continua vs. categórica
Para el ejemplo, usaremos un boxplot para comparar las variables Bodyweight y Diet.
ratones %>%
ggplot(aes(x = Diet, y = Bodyweight)) +
geom_boxplot()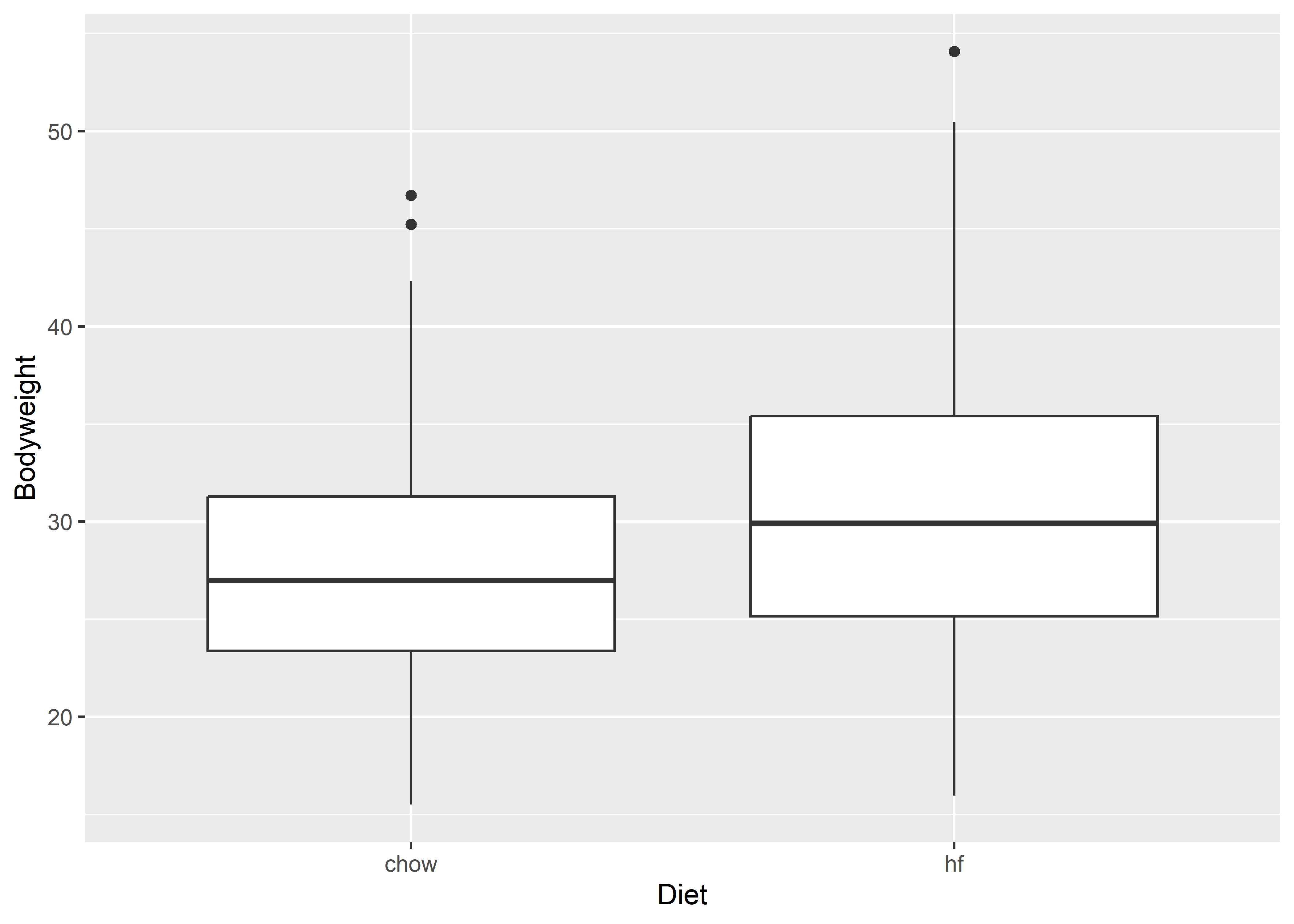
También podemos utilizar una geometría de violín.
ratones %>%
ggplot(aes(x = Diet, y = Bodyweight)) +
geom_violin()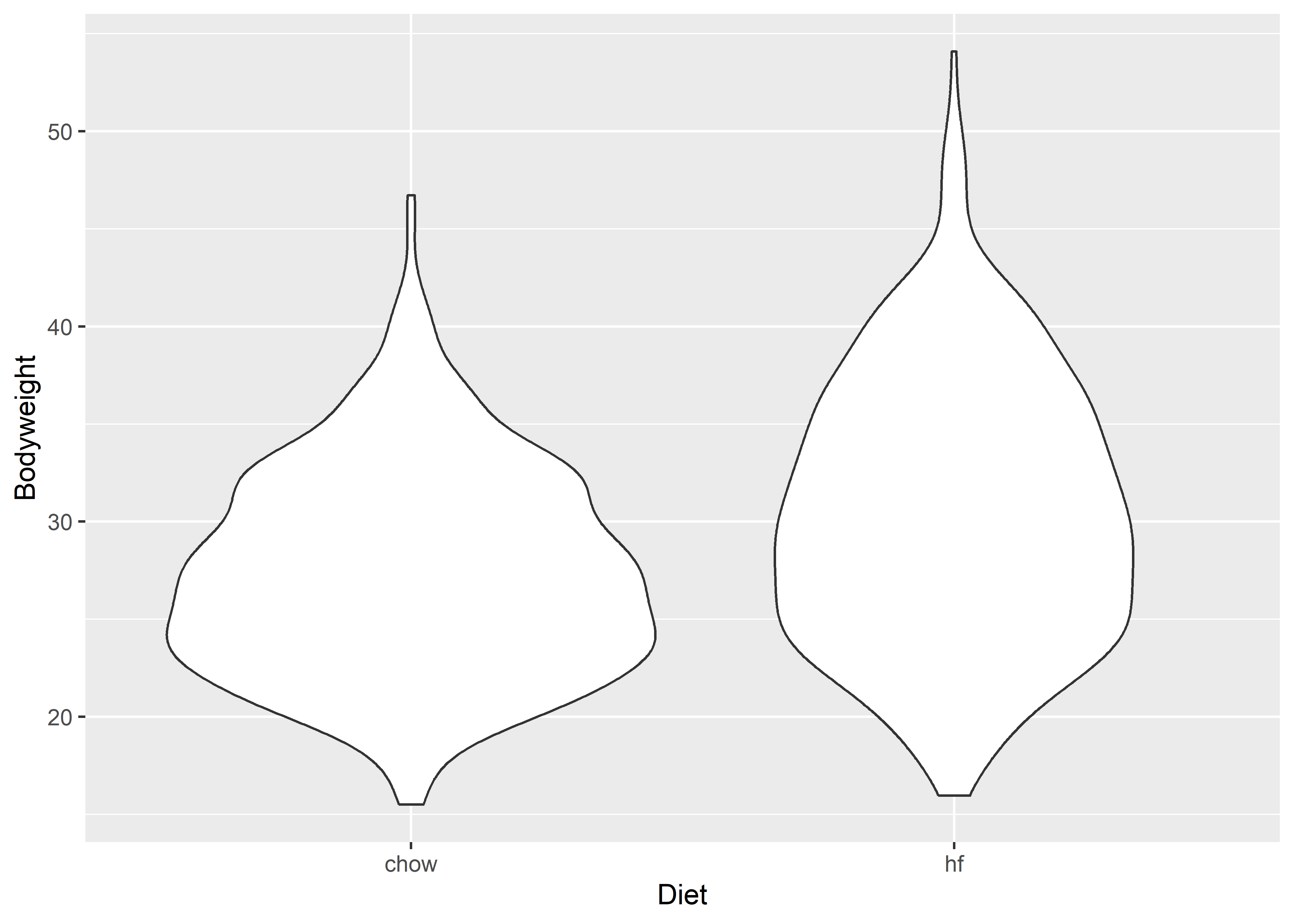
6.10 Ejercicios
Ejercicio 1
Realizar la exploración gráfica sobre la distribución de las variables consumo de energía (en_intake) y tiempo en días (time). Además, calcular los valores de la media, mediana, simetría y curtosis. Utilizar la geometría geom_vline() para complementar los gráficos. Finalmente, sustentar la conclusión sobre la forma de las distribuciones.
Ejercicio 2
Comparar la dispersión de las variables eficiencia metabólica (kJ/día por gramo de peso corporal) (meta_eff) y respuesta temprana a la insulina (pmol/l) (ein_resp) utilizando la(s) medida(s) de dispersión más adecuada(s).
Ejercicio 3
A) Explorar y comparar en_intake y ein_respen términos de asimetría.
B) Explorar y comparar insulin y meta_effen términos de curtosis.