19 Estudios de casos y controles
19.1 Paquetes y data
Los paquetes que se utilizarán son:
El archivo de datos dhs.csv contiene información relacionada a la salud materno-infantil y condiciones sociodemográficas en Perú. En este conjunto de datos, cada observación (una madre que tiene un hijo dentro del periodo de estudio) esta agrupada en comunidades. Estos datos son una submuestra de la Encuesta Demográfica y de Salud Familiar (ENDES). Para esta sección, exploraremos la relación entre agua segura para consumo (safe_water) y muerte infantil en menores de 1 mes de nacidos (death_1m)
peru <- read_csv("data/dhs.csv")19.2 Diseño de estudio
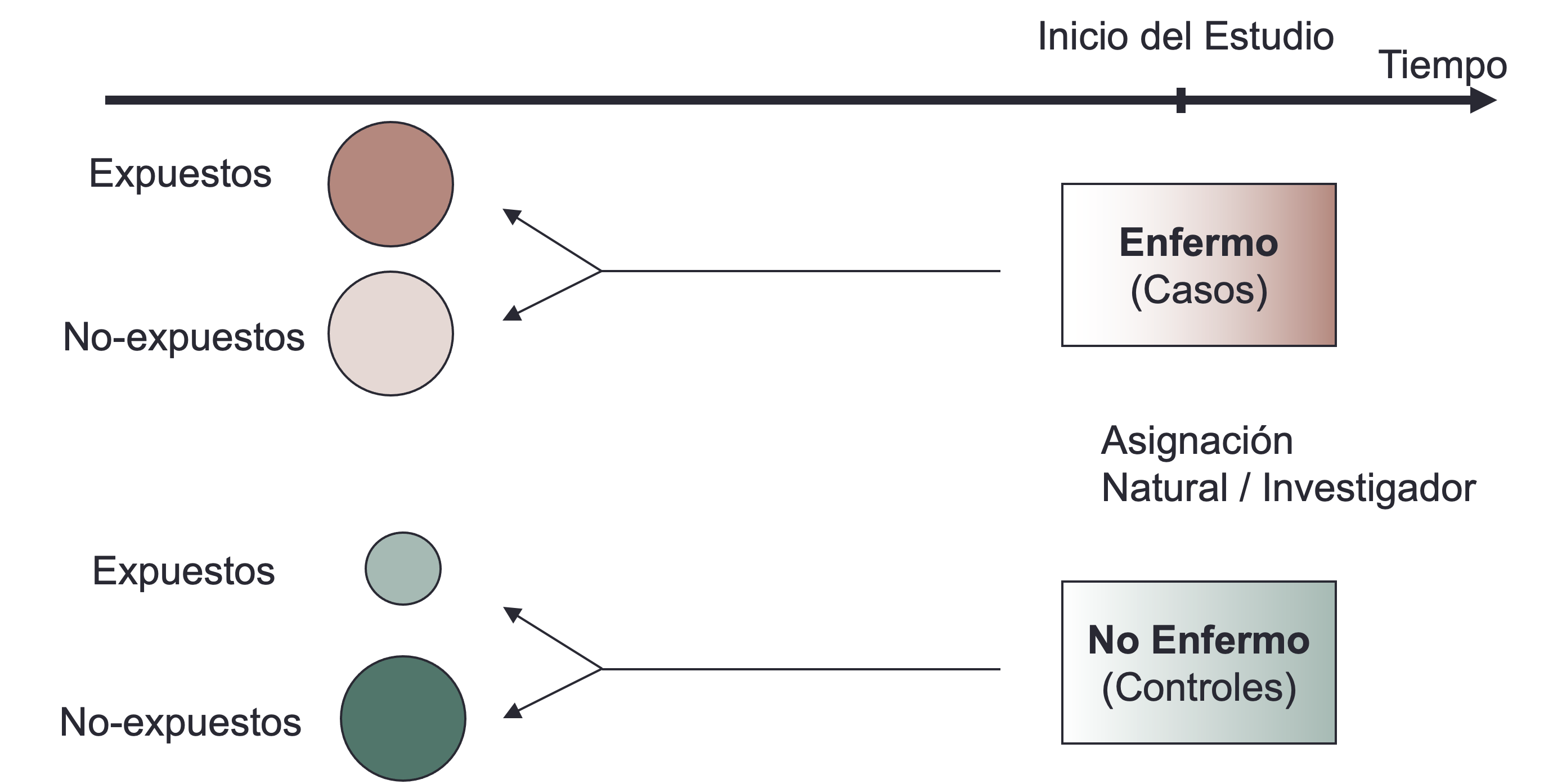
En este tipo de estudio, se investiga la relacion entre dos variables partiendo de la enfermedad ( desenlace ) y se explora los factores de exposición. Es usado en epidemiología para identificar factores que difieren en su frecuencia entre los casos y los controles
Esquema básico
Se selecciona un grupo de sujetos con la enfermedad (llamados “casos”).
Se selecciona otro grupo de personas sin la enfermedad (llamados “controles”).
Se determina la frecuencia de exposición en los casos y los controles, y se comparan los “odds” de la exposición entre ellos.
Las diferencias se interpretan como posibles factores asociados con la enfermedad.
Debido al diseño del estudio, la proporción de casos Ecuación 19.1 está definida por el investigador. En otras palabras, la frecuencia real de la enfermedad (ej. prevalencia, incidencia) real se desconoce.
\[ {Proporción \;casos} = \frac{Casos}{Casos + Controles} \tag{19.1}\]
Esta limitación (marco de datos ausentes) implica la creación de pseudo-frecuencias en base a distintos supuestos. En un estudio de casos y controles se seleccionan los controles para representar la distribución de exposición de la población fuente. Si la selección es exitosa, los denominadores pueden ser reemplazados para aproximarse a las frecuencias originales.
19.3 Selección de participantes
19.3.1 Selección de casos
Es importante identificar si se trabajará con casos incidentes (recién diagnosticados) o casos prevalentes (tiene la enfermedad desde hace un tiempo).
Si se usa casos prevalentes, habrá un mayor número de casos, pero dependerá de la supervivencia de la enfermedad.
Al trabajar con casos incidentes uno debe esperar a que se haga el diagnóstico. Se estará excluyendo a cualquier persona fallecida por la enfermedad antes de ser diagnosticada.
19.3.2 Selección de controles
Es uno de los procesos más delicados en el diseño de casos y controles. La selección de controles inadecuados puede invalidar los resultados del estudio. Los controles deben ser representativos de todas las personas sin la enfermedad.
Debe observarse estrictamente dos reglas básicas:
Los controles deben seleccionarse de la misma población que da origen a los casos de estudio. Si no se puede seguir esta regla, se requiere evidencia sólida de que la población que proporciona los controles tiene una distribución de exposición idéntica a la de la población que es la fuente de los casos; esta contingencia es muy difícil de demostrar y rara vez se cumple.
Dentro de los estratos de factores que se utilizarán para la estratificación en el análisis, los controles deben seleccionarse independientemente de su estado de exposición, es decir, la tasa de muestreo para los controles no debe variar con la exposición.
19.4 Emparejamiento
Es una restricción parcial en la selección de sujetos de estudio. Es un método utilizado en estudios observacionales para controlar el sesgo de confusión.
Restringe la elegibilidad de los sujetos de COMPARACIÓN para que sean similares a los sujetos ÍNDICE.
Las variables comunes son factores de riesgo para la enfermedad que también están relacionados con la exposición (CONFUSORES).
Otros factores logísticos tales como: momento del diagnóstico, lugar de residencia, centro médico, tiempo de seguimiento, etc.
19.4.1 Tipos de emparejamiento
Emparejamiento por frecuencia: el número seleccionado en cada categoría de emparejamiento del grupo de comparación (controles) se hace proporcional al número en esa categoría del grupo de índice (casos).
-
Emparejamiento individual: uno o más sujetos de comparación (controles) se seleccionan por separado para cada sujeto índice (casos).
Proporción variable: La proporción de sujetos de comparación (controles) con respecto a los sujetos índice (casos) varía (esto no suele ser por diseño, sino como resultado de la falta de participación).
Proporción fija: La proporción de sujetos de comparación (controles) con los sujetos índice (casos) es la misma para todos los conjuntos emparejados (p. ej., “por parejas”, 1:1, 1:2, etc.)
19.4.2 Procesamiento de datos
Para empezar, procesaremos el conjunto de datos para poner en formato las variables de interés.
Crearemos la variable provincia usando los primeros 2 dígitos del código de comunidad (
village). Usaremos la funciónstr_subdel paquete stringr que se encuentra dentro del tidyverse.
19.4.3 Emparejamiento por frecuencia
De nuestro conjunto de datos fuente seleccionaremos a todos los casos (madres que hayan registrado una muerte infantil en menores de 1 mes de nacidos - death_1m) y determinaremos la distribución de sus frecuecias de quintil de edad y seguro de salud.
Se hará un muestreo aleatorio de controles proporcional a la distribución de las frecuecias de quintil de edad y seguro de salud del grupo de casos. Tomaremos una muestra global de controles de 650 (ratio global 1:10).
Utilizaremos la función
map2del paquete purrr que se encuentra dentro del tidyverse para calcular una muestra dentro de cada grupo.
Finalmente uniremos los conjuntos de datos de casos y controles.
Verificamos si la muestra cumple los criterios de emparejamiento por frecuencias.
dat_f %>%
select(death_1m, age_cat, insurance, safe_water) %>%
cross_tbl(by = "death_1m", percent = "col")|
0, N = 650 |
1, N = 65 |
Overall, N = 715 |
|
|---|---|---|---|
| age_cat | |||
| [15,17] | 270 (42%) | 27 (42%) | 297 (42%) |
| (17,18] | 30 (4.6%) | 3 (4.6%) | 33 (4.6%) |
| (18,20] | 130 (20%) | 13 (20%) | 143 (20%) |
| (20,23] | 80 (12%) | 8 (12%) | 88 (12%) |
| (23,42] | 140 (22%) | 14 (22%) | 154 (22%) |
| insurance | |||
| 0 = no | 380 (58%) | 38 (58%) | 418 (58%) |
| 1 = yes | 270 (42%) | 27 (42%) | 297 (42%) |
| safe_water | |||
| No | 239 (37%) | 40 (62%) | 279 (39%) |
| Si | 411 (63%) | 25 (38%) | 436 (61%) |
Un estudio de casos y controles calcula el odds ratio (OR) de exposición, que es matemáticamente equivalente al OR de enfermedad.
Empezaremos la construcción de las tablas de contingencias
|
0, N = 650 |
1, N = 65 |
Overall, N = 715 |
|
|---|---|---|---|
| safe_water | |||
| No | 239 (37%) | 40 (62%) | 279 (39%) |
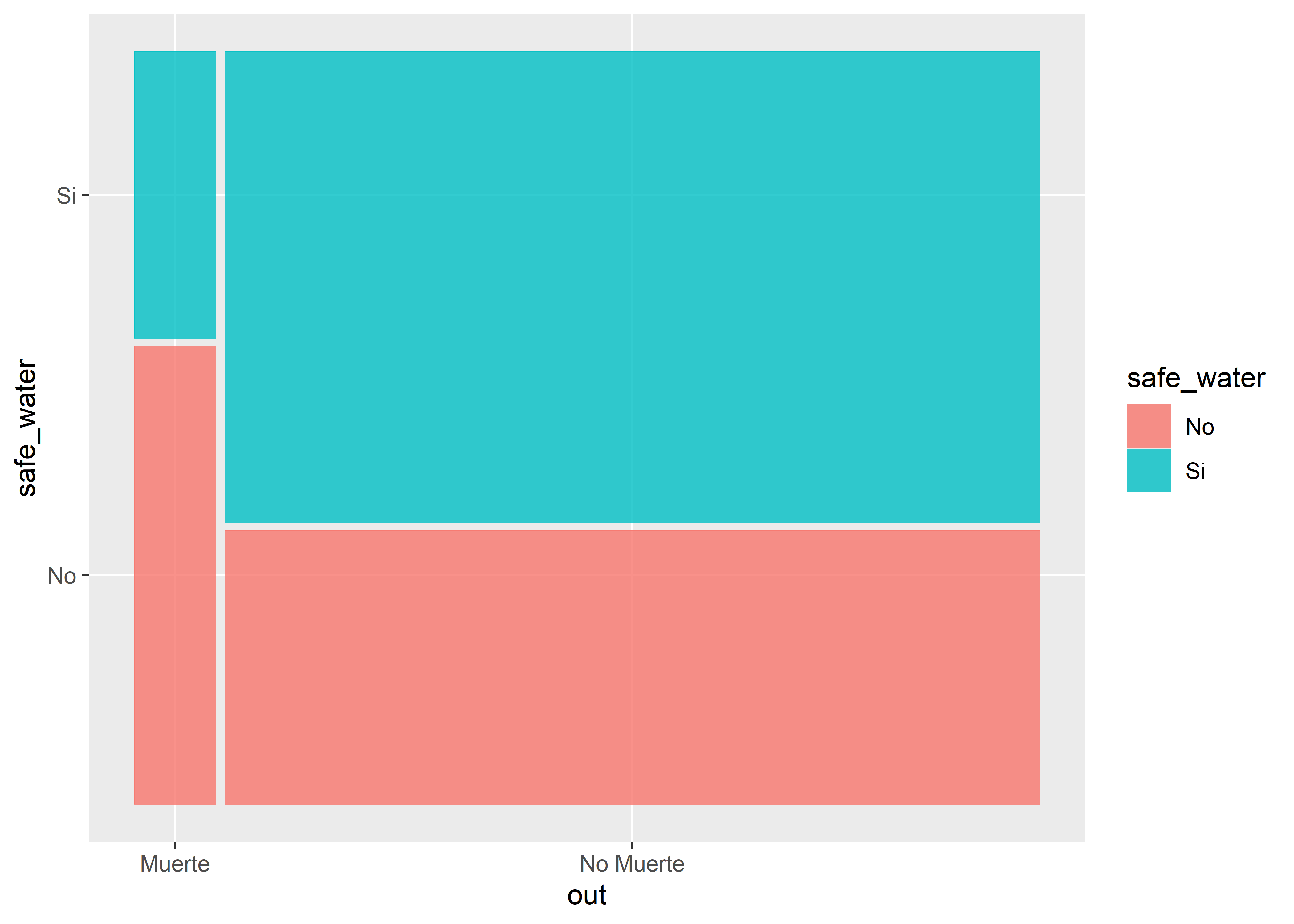
| Si | 411 (63%) | 25 (38%) | 436 (61%) |
Observamos que en el grupo de casos, la mayoría no tiene agua segura de consumo y que en el grupo de controles la mayoría sí la tiene.
dat_f %>%
contingency(death_1m ~ safe_water,
method = "case.control") Outcome
Predictor 1 0
Si 25 411
No 40 239
Outcome + Outcome - Total Odds
Exposed + 25 411 436 0.06 (0.04 to 0.09)
Exposed - 40 239 279 0.17 (0.12 to 0.23)
Total 65 650 715 0.10 (0.08 to 0.13)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Exposure odds ratio 0.36 (0.22, 0.61)
Attrib fraction (est) in the exposed (%) -174.74 (-385.20, -58.17)
Attrib fraction (est) in the population (%) -67.36 (-107.93, -34.71)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 15.236 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
Wald confidence limits
CI: confidence interval
Pearson's Chi-squared test with Yates' continuity correction
data: dat
X-squared = 14.213, df = 1, p-value = 0.0001633El resultado de las tablas de contingencia no toma en consideración el diseño de muestras emparejadas por frecuencias.
El análisis de los datos emparejados debe tener en cuenta las variables de emparejamiento a través de alguna forma de estratificación, por ejemplo, modelos multivariables.
Usaremos una regresión logística multivariable con el comando glm.
model <- glm(death_1m ~ safe_water + age_cat + insurance,
family="binomial", data = dat_f)| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| (Intercept) | 0.1583119 | 0.2422932 | -7.6072623 | 0.0000000 | 0.0963837 | 0.2498864 |
| safe_waterSi | 0.3580418 | 0.2696474 | -3.8090693 | 0.0001395 | 0.2087098 | 0.6033769 |
| age_cat(17,18] | 0.9288583 | 0.6446523 | -0.1144789 | 0.9088581 | 0.2111750 | 2.8812586 |
| age_cat(18,20] | 1.1024013 | 0.3590368 | 0.2715343 | 0.7859801 | 0.5304806 | 2.1916263 |
| age_cat(20,23] | 1.1202045 | 0.4364990 | 0.2600493 | 0.7948258 | 0.4492586 | 2.5382273 |
| age_cat(23,42] | 1.1139096 | 0.3532757 | 0.3053594 | 0.7600925 | 0.5442910 | 2.1960957 |
| insurance1 = yes | 1.0242004 | 0.2736274 | 0.0873897 | 0.9303618 | 0.5941684 | 1.7441624 |
Construiremos un gráfico de mosaico para comparar las dos variables categóricas. Usaremos la geometría geom_mosaic() del paquete ggmosaic
19.4.4 Emparejamiento Individual
Los casos serán definidos como aquellas madres en nuestro conjunto de datos peru que hayan registrado una muerte infantil en menores de 1 mes de nacidos (death_1m).
Los controles serán definidos como otras madres que vivan en la misma provincia, grupo de riqueza y quintil de edad.
Se realizará un emparejamiento individual con una proporción variable. El ratio máximo de casos:controles será de 1:3 (proporción variable).
Para determinar los grupos de emparejamiento usaremos el paquete MatchIt.
set.seed(2023)
peru_match <- matchit(death_1m ~ province + wealth_ind + age_cat,
exact = ~ province + wealth_ind + age_cat,
ratio = 3,
data = peru)
dat_m <- match.data(peru_match)Inspeccionamos la proporción de emparejamiento en los grupos de emparejamiento que se pudieron lograr.
dat_m %>%
group_by(subclass) %>%
count() %>%
ggplot(aes(x = n)) +
geom_bar() +
geom_label(stat = "count",
aes(label = after_stat(count)))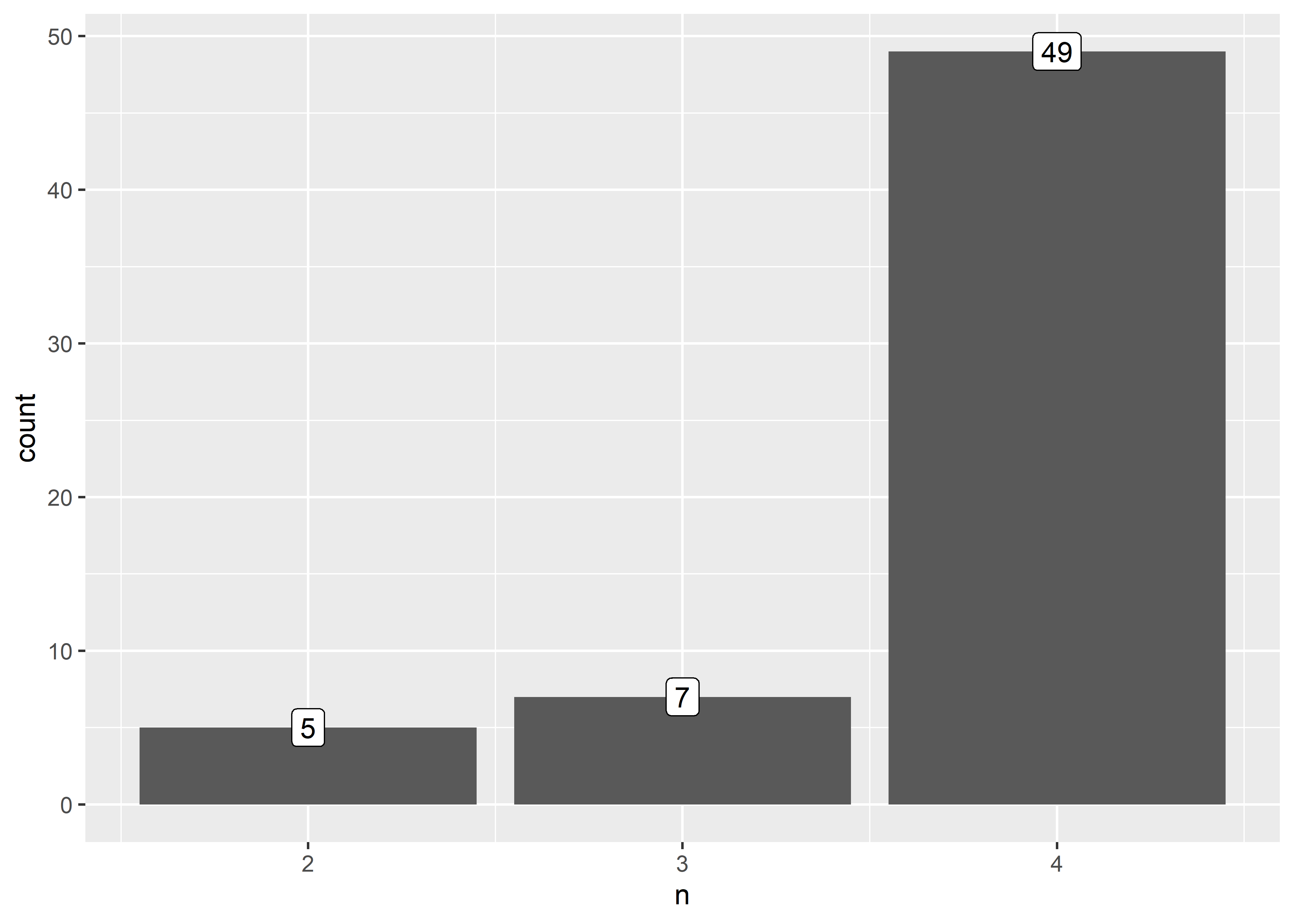
En este conjunto de datos se han podido emparejar (de forma individual):
- 49 casos con 3 controles.
- 7 casos con 2 controles.
- 5 casos con 1 control.
Debido al diseño analítico (proporción variable), utilizaremos todos los grupos de emparejamiento, 1:3, 1:2 y 1:1.
Empezaremos la construcción de las tablas de contingencias
|
0, N = 166 |
1, N = 61 |
Overall, N = 227 |
|
|---|---|---|---|
| safe_water | |||
| No | 83 (50%) | 38 (62%) | 121 (53%) |
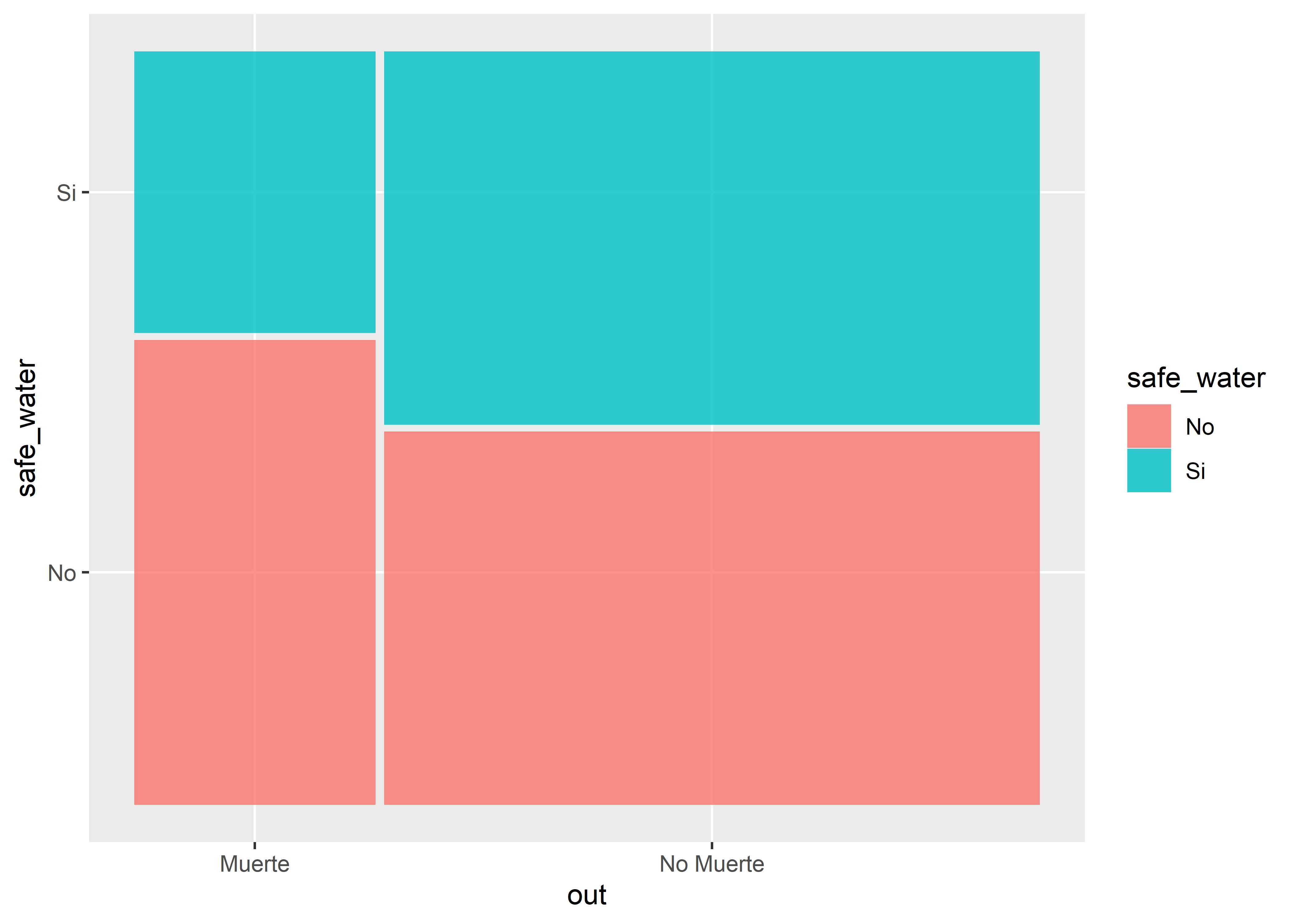
| Si | 83 (50%) | 23 (38%) | 106 (47%) |
Observamos que en grupo de casos la mayoría no tiene agua segura de consumo y que en el grupo de controles las frecuencias son iguales.
dat_m %>%
contingency(death_1m ~ safe_water,
method = "case.control") Outcome
Predictor 1 0
Si 23 83
No 38 83
Outcome + Outcome - Total Odds
Exposed + 23 83 106 0.28 (0.16 to 0.43)
Exposed - 38 83 121 0.46 (0.30 to 0.66)
Total 61 166 227 0.37 (0.27 to 0.48)
Point estimates and 95% CIs:
-------------------------------------------------------------------
Exposure odds ratio 0.61 (0.33, 1.10)
Attrib fraction (est) in the exposed (%) -64.85 (-216.95, 12.87)
Attrib fraction (est) in the population (%) -24.59 (-59.58, 2.73)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 2.709 Pr>chi2 = 0.100
Fisher exact test that OR = 1: Pr>chi2 = 0.133
Wald confidence limits
CI: confidence interval
Pearson's Chi-squared test with Yates' continuity correction
data: dat
X-squared = 2.2377, df = 1, p-value = 0.1347El resultado de las tablas de contingencia no toma en consideración el diseño de muestras emparejadas individualmente.
En estudios de casos y controles emparejados individualmente, solo los pares discordantes aportan información a la razón de odds (OR).
El análisis de los datos emparejados debe tener en cuenta las variables de emparejamiento a través de alguna forma de estratificación, por ejemplo, regresión logística condicional.
Usaremos una regresión logística condicional usando el comando clogit del paquete survival.
| term | estimate | std.error | statistic | p.value | conf.low | conf.high |
|---|---|---|---|---|---|---|
| safe_waterSi | 0.4787554 | 0.3645873 | -2.020272 | 0.0433552 | 0.2343022 | 0.9782525 |
Construiremos un gráfico de mosaico para comparar las dos variables categóricas. Usaremos la geometría geom_mosaic() del paquete ggmosaic
19.5 Ejercicios
Ejercicio 1
A) Usando el conjunto de datos peru (dhs.csv), realizar un emparejamiento individual en base a la provincia, grupo de riqueza y quintil de edad. Utilizar una proporción fija. Es decir, incluir solo a los casos que se hayan podido emparejar con 3 controles.
B) Comparar los resultados con el emparejamiento individual con proporción variable.
Ejercicio 2
A) Usando el conjunto de datos peru (dhs.csv), proponer una nueva estrategia de emparejamiento por frecuencia.
B) Comparar los resultados con el emparejamiento por frecuencia propuesto anteriormente.