Solucionario de ejercicios

Pipelines

dhs <- read_csv("data/dhs.csv")

Ejercicio 1

A) Escribir en lenguaje natural, que procedimientos se estan llevando a cabo en el siguiente codigo.

dhs_pipe2 <- dhs %>% 
  select(wealth_ind, literacy, educ_yrs, death_1m) %>%
  drop_na() %>%
  group_by(wealth_ind, literacy) %>%
  summarise(median_edu = median(educ_yrs), 
            tot_death = sum(death_1m), 
            pop = n()) %>%
  filter(tot_death>10)

De la base de datos dat, seleccionar las variables de interes (wealth_ind, literacy, educ_yrs, death_1m), luego filtrar aquellas observaciones con datos completos, luego agrupar los datos por categorias de nivel de ingreso y alfabetismo, luego calcular la mediana de años de educacion y el numero total de muertes neonatales en cada grupo y luego (finalmente) filtrar los grupos que tengan mas de 10 muertes neonatales.

B) ¿Que conclusiones podria sacar de este pipeline?

Los grupos de educacion e ingresos que tienen mas de 10 muertes neo-natales son los grupos desde el mas pobre hasta rico (1-4) que pueden leer almenos una oracion.

Ejercicio 2

A) Escribir el pipeline para la siguiente tarea de manejo de datos.

De la base de datos dhs, filtrar las observaciones de las madres menores de 20 años, luego remover todos las observaciones con valores ausentes (NA) en las variables edad, edad de pareja y seguro, luego calcular la diferencia entre la edad de la participante y la de su pareja, luego agrupar de acuerdo a si tienen seguro y acceso a agua potable segura, y luego calcular el promedio de hijos de las madres en cada una de estas categorias y la diferencia promedio de edad con sus parejas.

data_pipe3 <- dhs %>% 
  drop_na(partner_age, age, insurance) %>%
  filter(age<20) %>%
  mutate(diff_age = partner_age - age) %>%
  group_by(insurance, safe_water) %>%
  summarise(mean_child = mean(num_child), mean_diff = mean(diff_age))

B) ¿Que conclusiones podria sacar de este pipeline?

El grupo de mujeres sin seguro de salud y sin agua potable segura, son aquellas con la menor diferencia de años con su pareja. El promedio de hijos es muy similar en las categorias de seguro de salud y acceso a agua potable segura.

ggplot

Ejercicio 1

A) Usando la base de datos who explorar la relación entre la inteisdad de emisiones de CO2 debido a actividades económicas (co2_economic_output) y malnutrición infantil (malnutrition_weight_age). Diferenciar los paises de acuerdo al continente (continent) donde se encuentran localizado

who <- read_csv("data/who.csv")

who %>%
  ggplot(aes(x = co2_economic_output, y = malnutrition_weight_age, 
             col = continent)) +
  geom_point()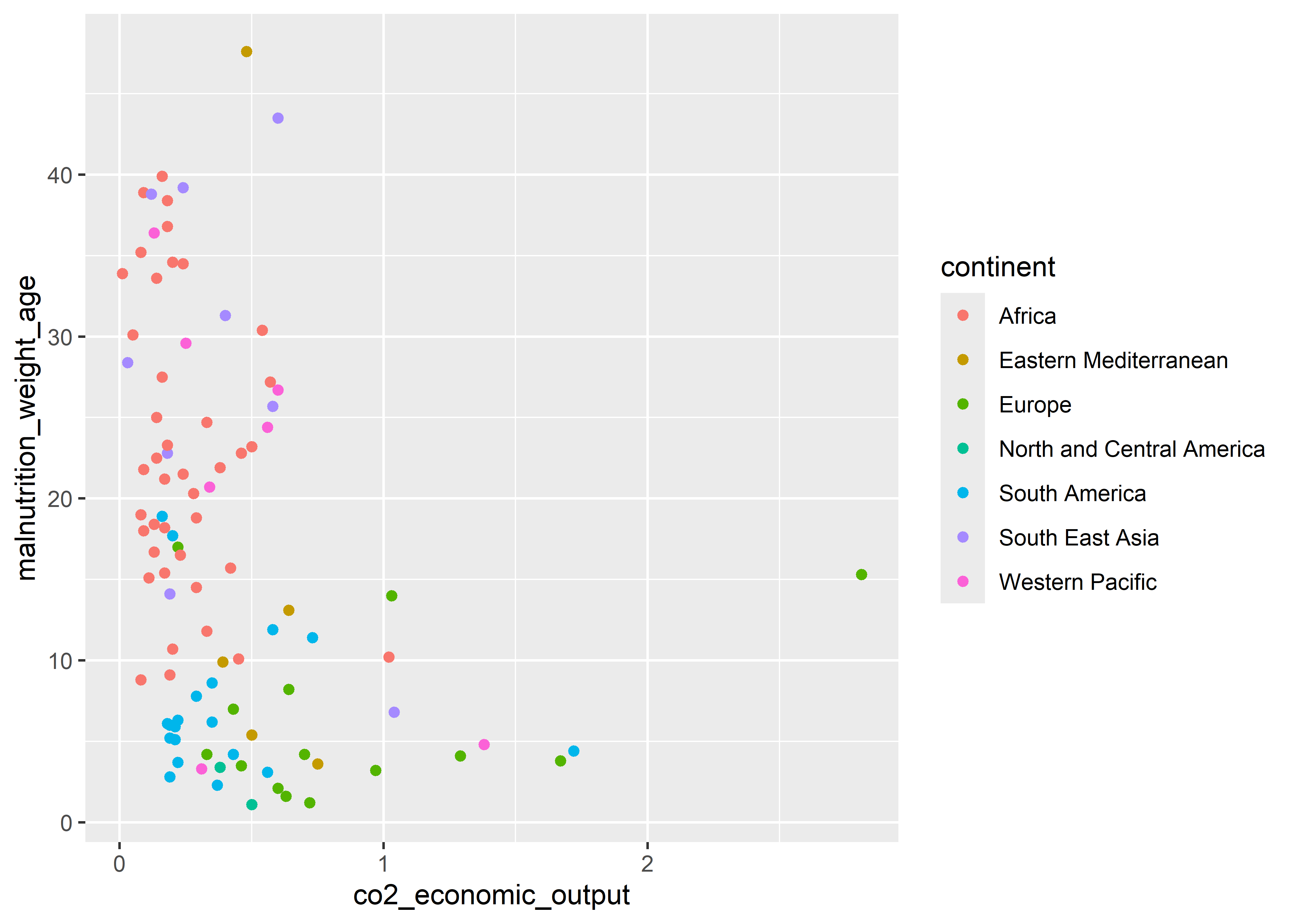

B) Que conclusiones podría sacar de este gráfico

Los paises del continente Africano tiene un perfil con alta malnutrición infantil y baja inteisdad de emisiones de CO2 debido a actuvidades económicas. Por lo contrario, los países Europeos muestran un perfil con baja malnutrición infantil y alta inteisdad de emisiones de CO2 debido a actividades económicas. Existe una tendencia de que aquellos paises donde hay mayor inteisdad de emisiones de CO2 debido a actividades económicas tiene una menor tasa de malnutrición infantil. No hay una estructura causal detrás de este análisis por lo que no se puede sugerir que la “manipulación” de alguna de estas variables generará cambios en la otra. En caso no exita suficiente información de alguna de malnutrición infantil, la inteisdad de emisiones de CO2 debido a actividades económicas podría ser un buen proxy.

Ejercicio 2

A) Reproducir el siguiente gráfico que muestra la diferencia en la distribución de camas hospitalarias (hospital_beds) en los diferentes quintiles de gasto en salud (contruir en base a la variable health_expenditure_gdp).

who %>%
  drop_na(health_expenditure_gdp) %>%
  mutate(cat_exp = cut_number(health_expenditure_gdp, 5)) %>%
  ggplot(aes(x = hospital_beds, y = cat_exp)) +
  geom_violin(fill = "gray") +
  geom_point(aes(color = cat_exp)) +
  theme_bw() +
  scale_color_brewer(palette = "Reds") +
  labs(x = "Camas Hospitalarias", y = "Quintiles de Gasto en Salud",
       color = "Quintiles de Gasto en Salud")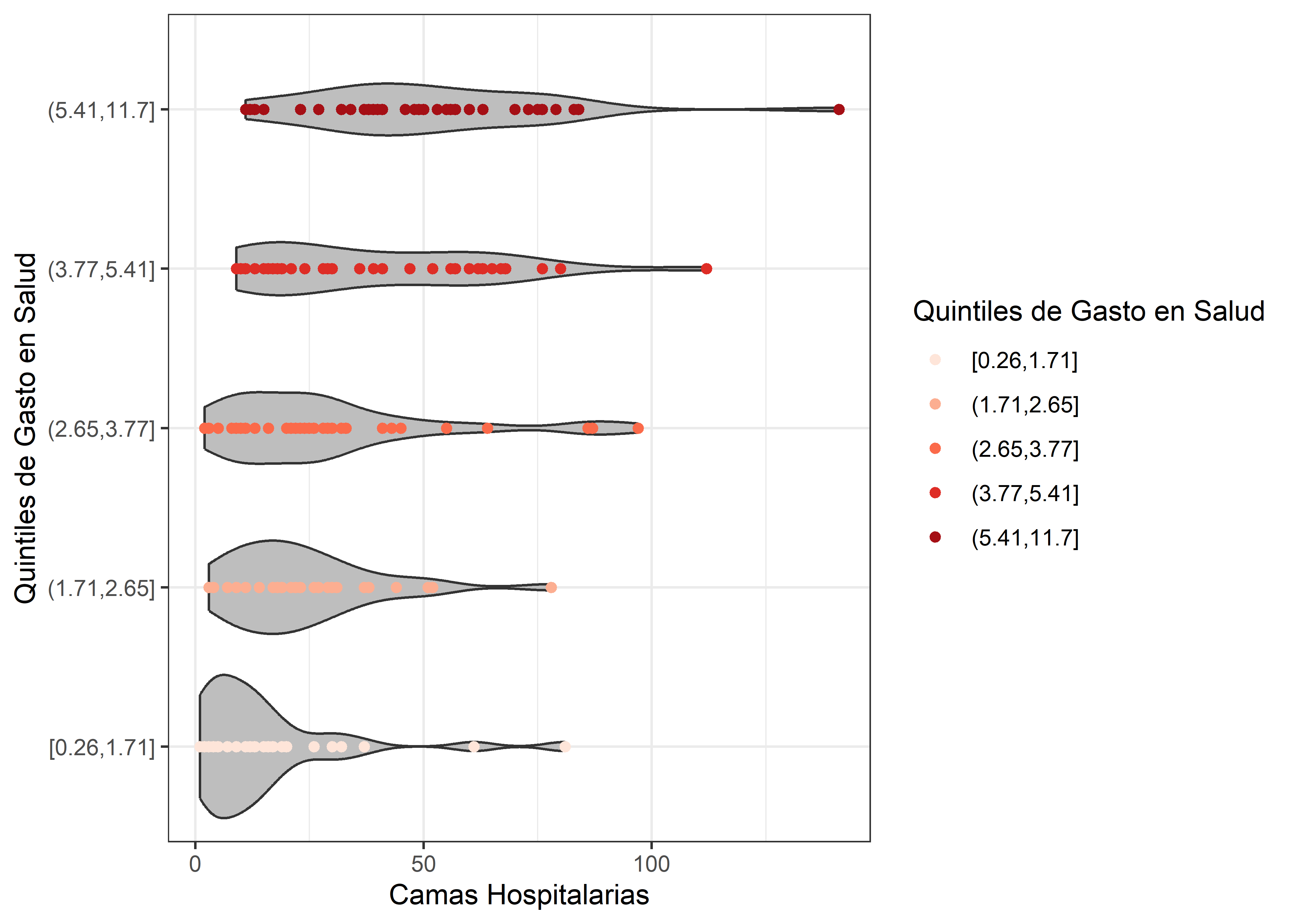

Analisis Exploratorio de Datos (AED)

ratones <- read_csv("data/ratones.csv")

library(pracma)
library(moments)

Ejercicio 1

Realizar la exploración gráfica sobre la distribución de las variables consumo de energía (en_intake) y tiempo en dias (time). Además, calcule los valores de la media, mediana, simetría y curtosis. Utiliza la geometría geom_vline() para complementar los gráficos. Finalmente, sustente su conclusión sobre la forma de las distribuciones.

Para en_intake:

ratones %>%
  ggplot(aes(x = en_intake)) +
  geom_boxplot(width = 10) + 
  geom_histogram(fill="transparent", col = "black") +
  geom_vline(aes(xintercept = mean(en_intake)), col = "red") +
  geom_vline(aes(xintercept = median(en_intake)), col = "blue") +
  geom_vline(aes(xintercept = Mode(en_intake)), col = "green")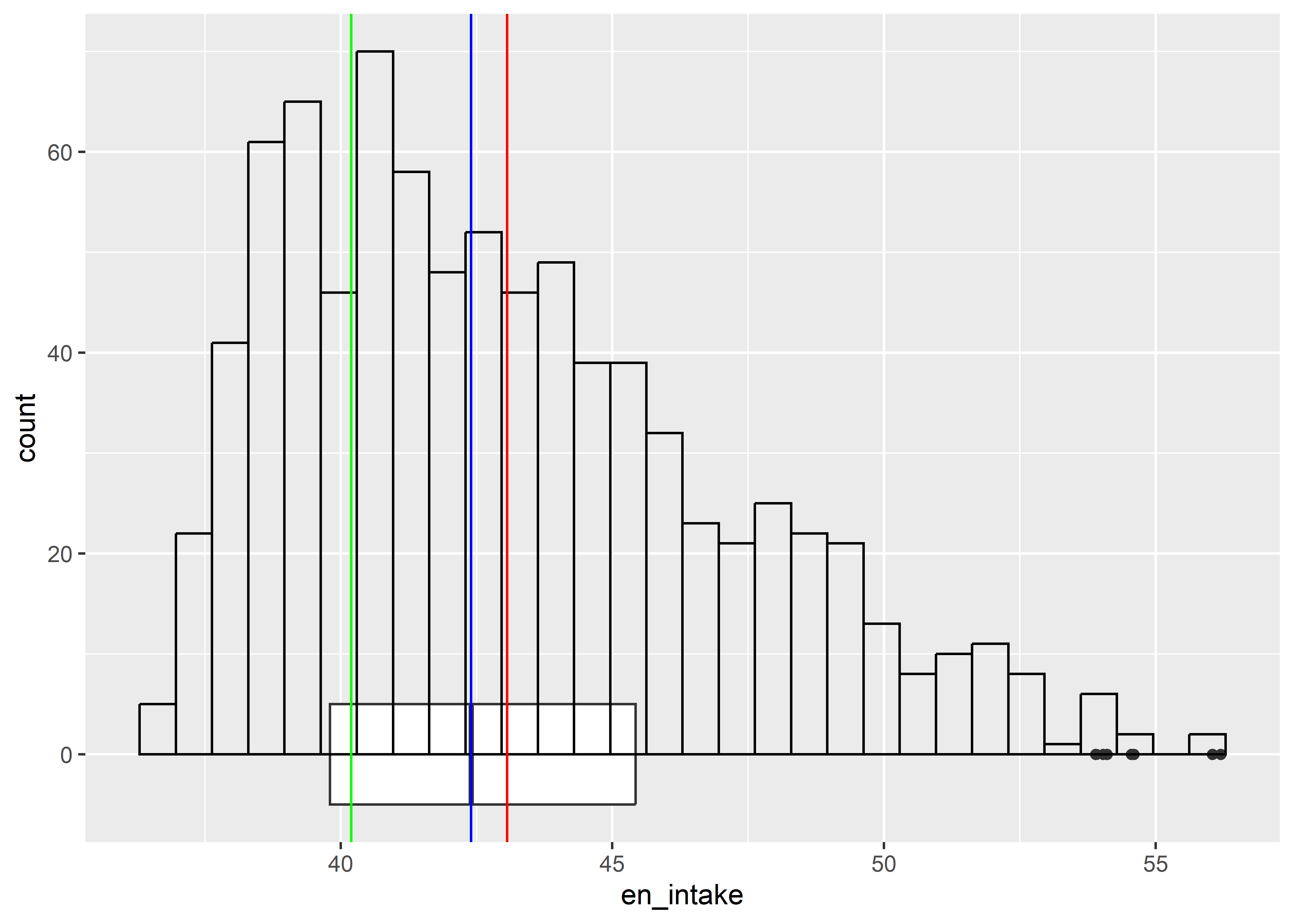

Para time:

ratones %>%
  ggplot(aes(x = time)) +
  geom_boxplot(width = 10) + 
  geom_histogram(fill="transparent", col = "black") +
  geom_vline(aes(xintercept = mean(time)), col = "red") +
  geom_vline(aes(xintercept = median(time)), col = "blue") +
  geom_vline(aes(xintercept = Mode(time)), col = "green")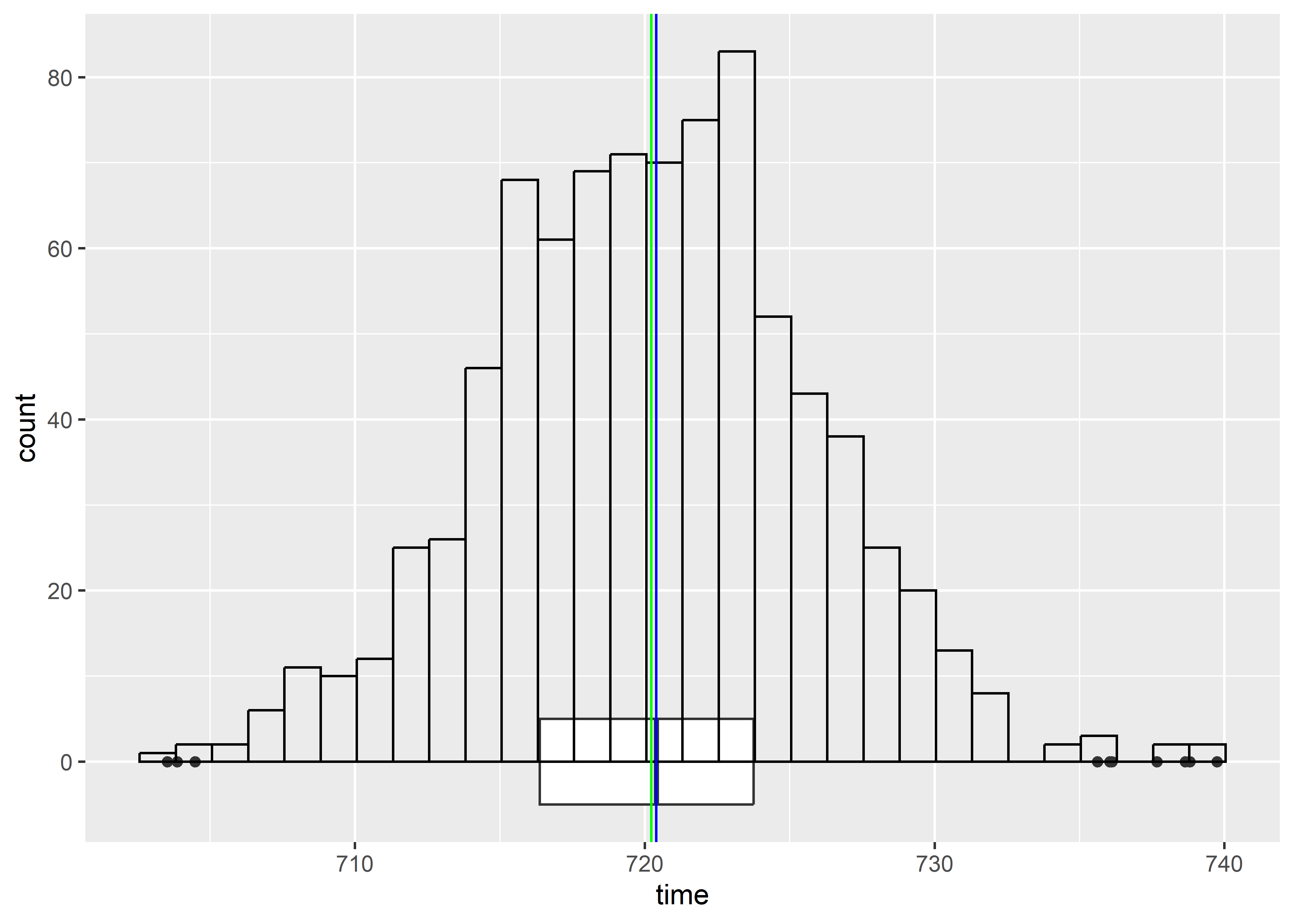

De acuerdo a la exploración gráfica y las diferentes medidas de tendencia central la variable time tiene distribucion nomal y la variable en_intake tiene un sesgo a la derecha (positivo).

Ejercicio 2

Comparar la dispersión de las variables eficiencia metabólica (kJ/día por gramo de peso corporal) (meta_eff) y respuesta temprana a la insulina (pmol/l) (ein_resp) utilizando la(s) medida(s) de dispersión más adecuada(s).

Para meta_eff:

ratones %>%
  ggplot(aes(x = meta_eff)) +
  geom_boxplot(width = 10) + 
  geom_histogram(fill="transparent", col = "black") +
  geom_vline(aes(xintercept = mean(meta_eff)), col = "red") +
  geom_vline(aes(xintercept = median(meta_eff)), col = "blue") +
  geom_vline(aes(xintercept = Mode(meta_eff)), col = "green")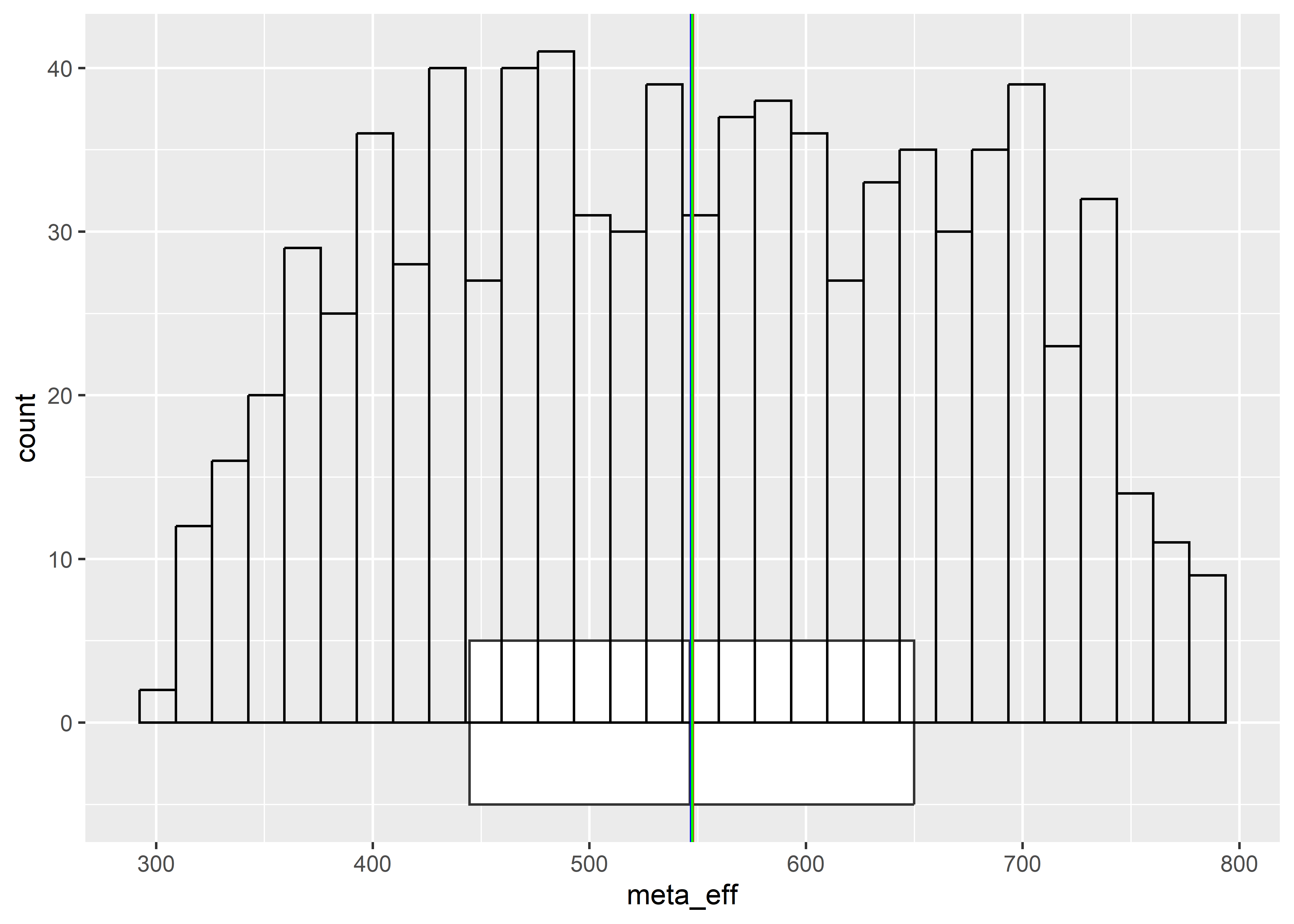

ratones %>%
  estat(~ meta_eff)
             N    Min    Max   Mean Median     SD   CV
1 meta_eff 846 307.74 792.26 547.78 546.88 123.09 0.22

Para ein_resp:

ratones %>%
  ggplot(aes(x = ein_resp)) +
  geom_boxplot(width = 10) + 
  geom_histogram(fill="transparent", col = "black") +
  geom_vline(aes(xintercept = mean(ein_resp)), col = "red") +
  geom_vline(aes(xintercept = median(ein_resp)), col = "blue") +
  geom_vline(aes(xintercept = Mode(ein_resp)), col = "green")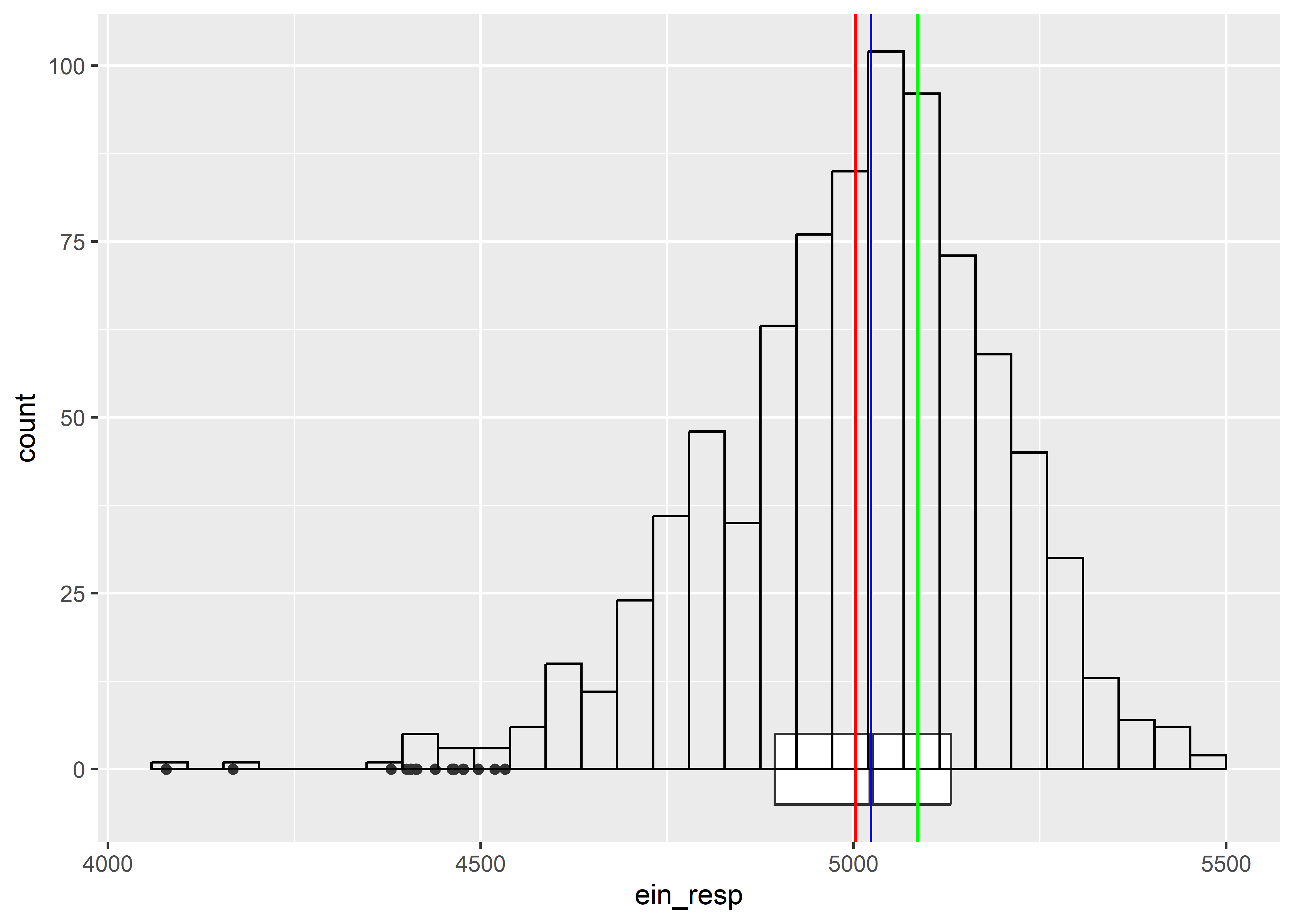

ratones %>%
  estat(~ ein_resp)
             N     Min     Max    Mean  Median    SD   CV
1 ein_resp 846 4078.18 5471.18 5002.99 5023.54 191.3 0.04

De acuerdo a la exploración gráfica la variable meta_eff tiene una mayor dispersion que la variable ein_resp. Sin embargo, las medidas de dispersion tradicionales muestran que ein_resp tiene una mayor desviacion standard (sd) y varianza (var) que meta_eff. Estas mediciones estan influenciadas por la escala de ambas variables. Al calcular el coeficiente de variacion (cv) se observa que el cv meta_eff = 0.2247065 > ein_resp = 0.03823714.

Ejercicio 3

A) Explorar y comparar en_intake y ein_respen términos de asimetría.

Para en_intake:

ratones %>%
  ggplot(aes(x = en_intake)) +
  geom_boxplot(width = 10) + 
  geom_histogram(fill="transparent", col = "black") +
  geom_vline(aes(xintercept = mean(en_intake)), col = "red") +
  geom_vline(aes(xintercept = median(en_intake)), col = "blue") +
  geom_vline(aes(xintercept = Mode(en_intake)), col = "green")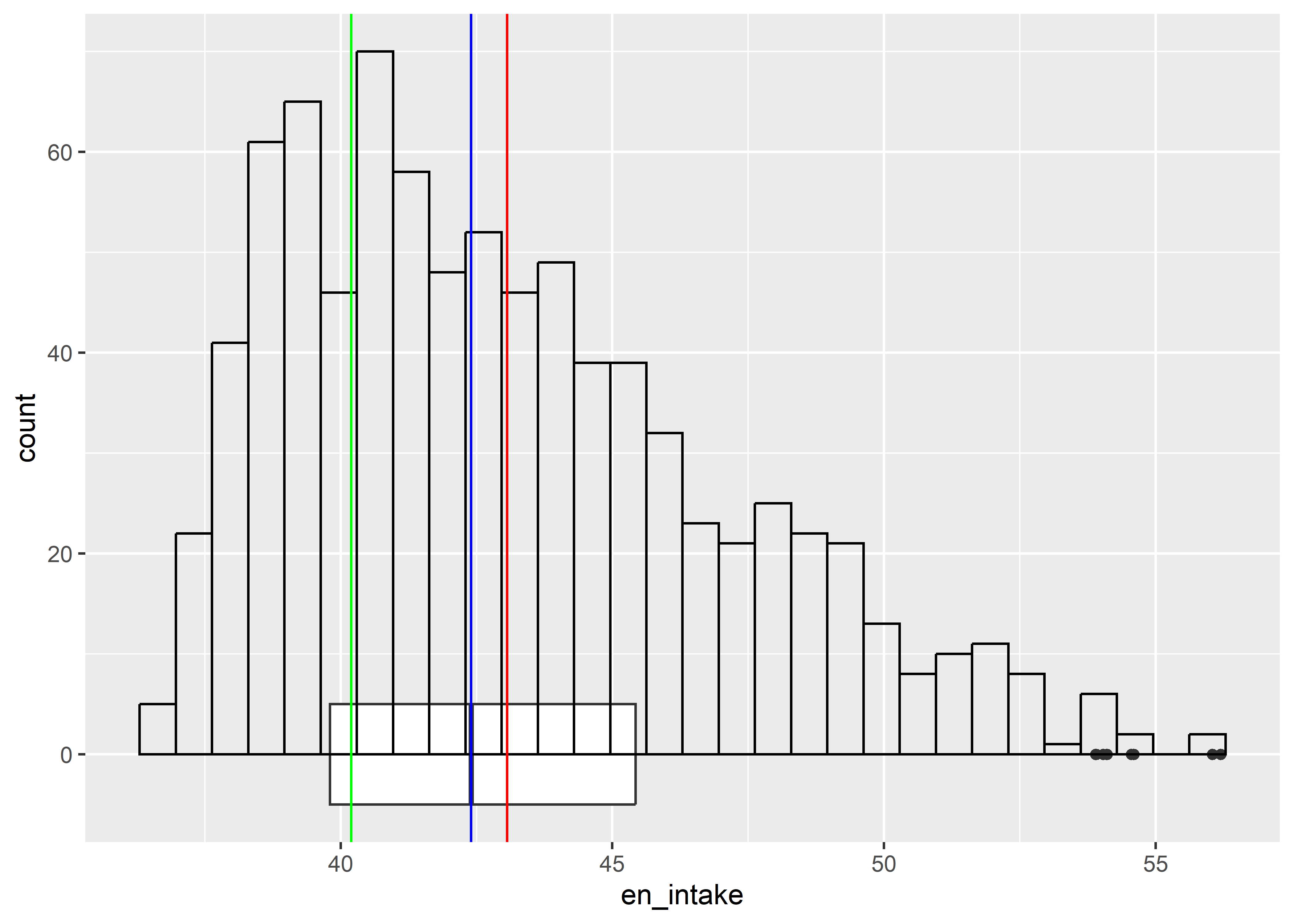

skewness(ratones$en_intake)
[1] 0.7060313

Para ein_resp:

ratones %>%
  ggplot(aes(x = ein_resp)) +
  geom_boxplot(width = 10) + 
  geom_histogram(fill="transparent", col = "black") +
  geom_vline(aes(xintercept = mean(ein_resp)), col = "red") +
  geom_vline(aes(xintercept = median(ein_resp)), col = "blue") +
  geom_vline(aes(xintercept = Mode(ein_resp)), col = "green")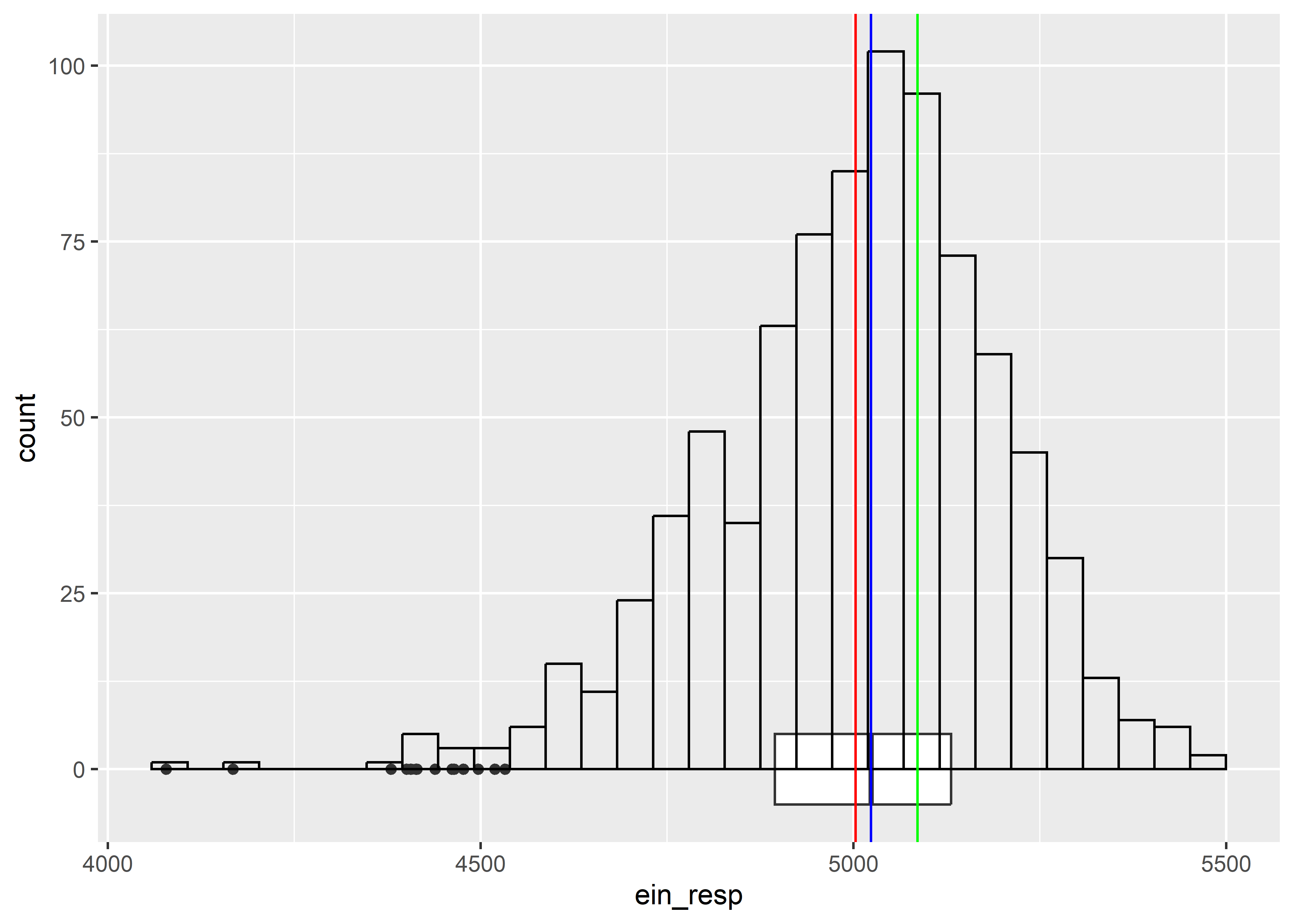

skewness(ratones$ein_resp)
[1] -0.6105134

De acuerdo a la inspeccion grafica la variable en_intake tiene un sesgo a la derecha (positivo) [Moda<Mediana<Media]. Por otro lado, la variable ein_resp tiene un sesgo a la izquierda (negativo) [Moda>Mediana>Media].

B) Explorar y comparar insulin y meta_effen términos de curtosis.

Para insulin:

ratones %>%
  ggplot(aes(x = insulin)) +
  geom_boxplot(width = 10) + 
  geom_histogram(fill="transparent", col = "black") +
  geom_vline(aes(xintercept = mean(insulin)), col = "red") +
  geom_vline(aes(xintercept = median(insulin)), col = "blue") +
  geom_vline(aes(xintercept = Mode(insulin)), col = "green")

kurtosis(ratones$insulin)
[1] 4.090441

Para meta_eff:

ratones %>%
  ggplot(aes(x = meta_eff)) +
  geom_boxplot(width = 10) + 
  geom_histogram(fill="transparent", col = "black") +
  geom_vline(aes(xintercept = mean(meta_eff)), col = "red") +
  geom_vline(aes(xintercept = median(meta_eff)), col = "blue") +
  geom_vline(aes(xintercept = Mode(meta_eff)), col = "green")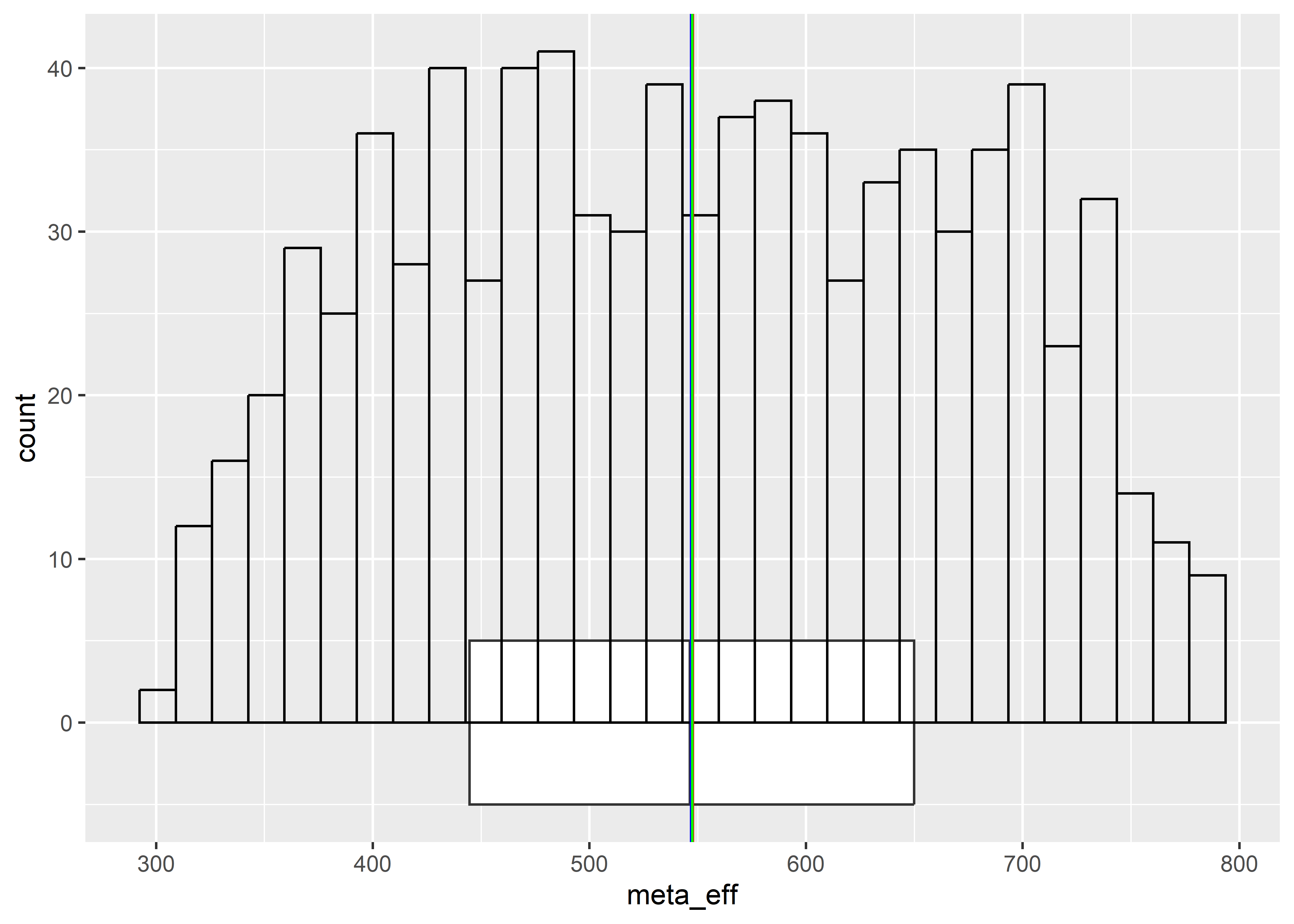

kurtosis(ratones$ein_resp)
[1] 4.027426

De acuerdo a las medidas de tendencia central, ambas variables insulin y meta_eff tienen la Media, Moda y Mediana muy cercanas, sugiriendo que ambas tienen distribucion normal. Sin embargo, al realizar la inspeccion gráfica y medición de la kurtosis observamos que insulin es leptocurtica y meta_eff es platicurtica.

Resumen de variables

var mean median mode sd cv skew kurt type
Bodyweight 28.847038 28.19000 26.070000 6.260434 0.2170217 0.5567657 3.138633 S. derecha
glucose 7.006728 7.00021 7.029131 0.383118 0.0546786 0.0012147 3.355597 Normal
en_intake 43.066220 42.39931 40.193526 3.971329 0.0922145 0.7060313 2.880872 S. derecha
insulin 497.116404 494.06867 496.967784 110.452824 0.2221870 0.0586389 4.090441 Normal, Lepto
meta_eff 547.776213 546.87788 547.531554 123.088855 0.2247065 0.0053068 1.940977 Normal, Plat
ein_resp 5002.985187 5023.54299 5086.226871 191.299835 0.0382371 -0.6105134 4.027426 S. izquierda
time 720.225261 720.39538 720.218237 5.588546 0.0077594 0.0396712 3.247685 Normal

Exactitud y precisión

Ejercicio 1

Carguemos el conjunto de datos:

data("ChickWeight")
View(ChickWeight)

Llamemos a tidyverse para poder hacer el procesamiento que se indica en el ejercicio:

Ahora, debemos calcular el promedio de las observaciones por cada pollito dada la dieta que recibió:

chick <- ChickWeight %>% 
  group_by(Chick, Diet) %>%  
  summarise(mean_weight = mean(weight))
`summarise()` has grouped output by 'Chick'. You can override using the
`.groups` argument.
View(chick)

Procedemos a calcular las estimaciones la media del peso promedio de los pollitos durante el experimento para cada tipo de dieta y sus errores estándar:

chick_mean <- chick %>% 
  group_by(Diet) %>%  
  summarise(
    n = n(), 
    sd = sd(mean_weight), 
    sample_mean = mean(mean_weight)
  ) |> 
  mutate(se = sd / sqrt(n))

chick_mean
# A tibble: 4 × 5
  Diet      n    sd sample_mean    se
  <fct> <int> <dbl>       <dbl> <dbl>
1 1        20  31.1        98.1  6.95
2 2        10  31.4       123.   9.94
3 3        10  27.3       143.   8.63
4 4        10  16.2       135.   5.11

Grafiquemos las estimaciones y sus errores estándar:

chick_mean %>% 
  ggplot(aes(x = Diet, y = sample_mean, col = Diet)) +
  geom_point(size = 4) +
  geom_errorbar(
    aes(ymin = sample_mean - se, ymax = sample_mean + se), width = 0.1
  )

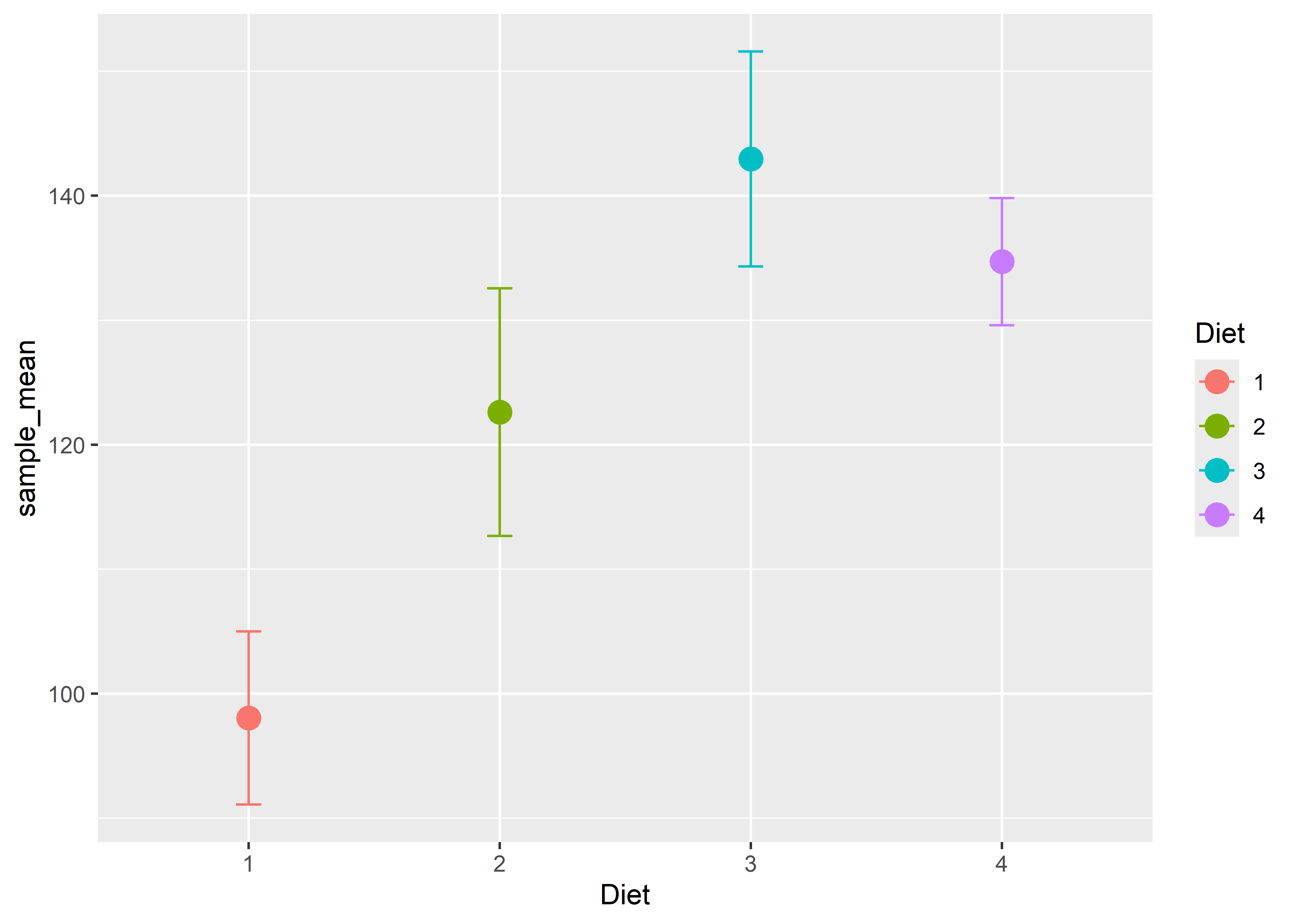
Se observa que la media estimada del peso promedio de los pollitos durante el experimento fue mayor en el grupo que recibió la dieta 3 (142.95$\(8.63 gramos), seguida de la dieta 4 (134.71\)\(5.11 gramos), la dieta 2 (122.62\)\(9.94 gramos) y, por último, la dieta 1 (98.05\)$6.95 gramos). Vemos también que la estimación del grupo de la dieta 2 tiene el mayor error estándar (menor precisión), mientras que la estimación de grupo de la dieta 4 tiene el menor error estándar (mayor precisión).

Ahora, para calcular los intervalos de confianza para cada grupo, podemos usar la función t_test() del paquete rstatix. Cargamos el paquete y procedemos a realizar los cálculos:


Attaching package: 'rstatix'
The following object is masked from 'package:stats':

    filter
chick_ci <- chick %>% 
  group_by(Diet) %>% 
  t_test(mean_weight ~ 1, detailed = TRUE) %>% 
  select(Diet, estimate, conf.low, conf.high)

chick_ci
# A tibble: 4 × 4
  Diet  estimate conf.low conf.high
  <fct>    <dbl>    <dbl>     <dbl>
1 1         98.1     83.5      113.
2 2        123.     100.       145.
3 3        143.     123.       162.
4 4        135.     123.       146.

Graficamos los intervalos de confianza para las estimaciones de la media del peso promedio de los pollitos durante el experimento:

chick_ci %>% 
  ggplot(aes(x = Diet, y = estimate, color = Diet)) +
  geom_point(size = 4) +
  geom_pointrange(aes(ymin = conf.low, ymax = conf.high))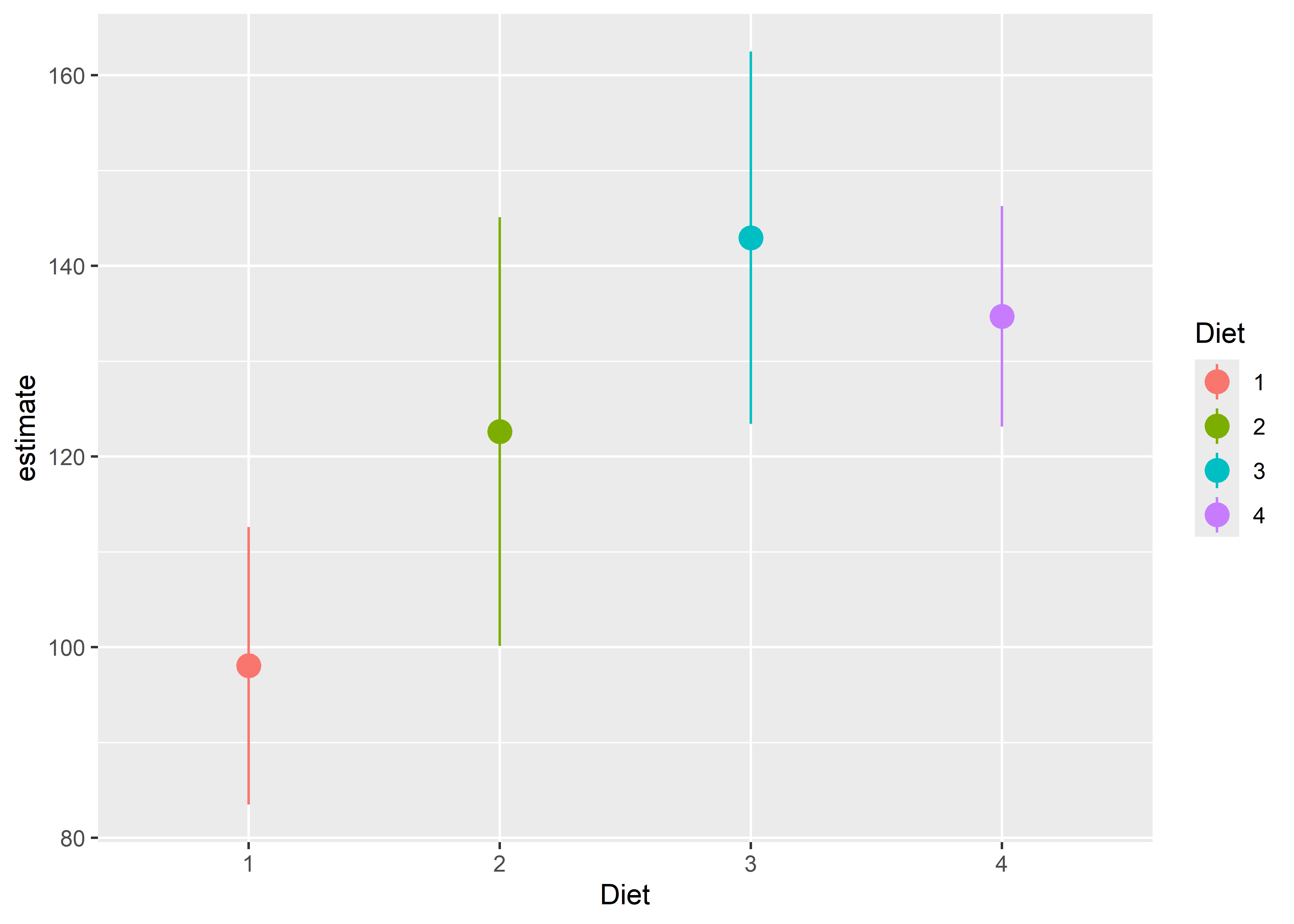

De este gráfico podemos llegar a las mismas conclusiones con respecto a la precisión de las estimaciones que con el gráfico anterior usando los errores estándar. Sin embargo, la interpretación de los intervalos de confianza es diferente. Aquí podemos decir, por ejemplo, que con un 95% de confianza, se estima que la media del peso promedio de los pollitos que reciben la dieta 3 se encuentra entre los 123.42 y 162.47 gramos.

Ejercicio 2

Carguemos los datos:

fev <- read_csv("data/fev.csv")
Rows: 654 Columns: 6
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (6): id, age, fev, hgt, sex, smoke

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Ejecutemos los modelos:

regre_model_fit_1 <- lm(fev ~ age + hgt, data = fev)
regre_model_fit_2 <- lm(fev ~ age + poly(hgt, 2) + sex, data = fev)
library(mgcv)
Loading required package: nlme

Attaching package: 'nlme'
The following object is masked from 'package:dplyr':

    collapse
This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.

Attaching package: 'mgcv'
The following object is masked from 'package:pracma':

    magic
regre_model_fit_3 <- gam(fev ~ s(age) + s(hgt), data = fev)

Las mismas funciones vistas para los modelos de regresión lineal se pueden usar para los GAM.

Llamemos al paquete broom para poder usar la función augment() y calcular los valores predichos:

regre_model_pred_1 <- regre_model_fit_1 %>% 
  augment() %>% 
  select(obs = fev, pred = .fitted)

regre_model_pred_2 <- regre_model_fit_2 %>% 
  augment() %>% 
  select(obs = fev, pred = .fitted)

regre_model_pred_3 <- regre_model_fit_3 %>% 
  augment() %>% 
  select(obs = fev, pred = .fitted)

regre_models_predictions <- bind_rows(
  list(
    "model_1" = regre_model_pred_1, "model_2" = regre_model_pred_2, 
    "model_3" = regre_model_pred_3
  ), 
  .id = "model"
)

Ahora, caguemos el paquete yardstick que contiene las funciones para el cálculo de diversas medidas para expresar el error de predicción:


Attaching package: 'yardstick'
The following object is masked from 'package:readr':

    spec

Con las medidas solicitadas en el ejercicio, definamos un conjunto de medidas:

metrics_regression <- metric_set(rmse, mae, mape)

Por último, realicemos el cálculo de las medidas para cada uno de los modelos:

regre_models_predictions %>% 
  group_by(model) %>%
  metrics_regression(truth = obs, estimate = pred) 
# A tibble: 9 × 4
  model   .metric .estimator .estimate
  <chr>   <chr>   <chr>          <dbl>
1 model_1 rmse    standard       0.419
2 model_2 rmse    standard       0.395
3 model_3 rmse    standard       0.393
4 model_1 mae     standard       0.319
5 model_2 mae     standard       0.297
6 model_3 mae     standard       0.294
7 model_1 mape    standard      12.7  
8 model_2 mape    standard      11.7  
9 model_3 mape    standard      11.6

Observamos que, según todas las medidas, el modelo aditivo generalizado (model_3) tiene un menor error de predicción, seguido muy cercanamente por el modelo con efecto polinomial para la altura (model_2), mientras que el modelo con solo efectos lineales para ambos predictores (model_1) es claramente inferior que los dos anteriores. Dados estos resultados, por el principio de parsimonia (escoger el modelo más simple que tenga un buen ajuste o poder predictivo) podríamos preferir el model_2 al model_3, ya que el último es más complejo de interpretar.

Ejercicio 3

Cargamos los datos:

data("Bernard", package = "pubh")
View(Bernard)

Realicemos las operaciones que se indican en el ejercicio:

sepsis <- Bernard %>% 
  drop_na() %>% 
  mutate(fate = factor(fate, levels = c("Alive", "Dead")))
class_model_fit_1 <- glm(
  fate ~ treat + race + apache, family = binomial, data = sepsis
)
class_model_fit_2 <- glm(
  fate ~ treat + race + apache + o2del, family = binomial, data = sepsis
)
class_model_fit_3 <- glm(
  fate ~ treat + race + apache + o2del + temp0, family = binomial, data = sepsis
)
class_model_pred_1 <- class_model_fit_1 %>% 
  augment(type.predict = "response") %>% 
  mutate(pred_class = ifelse(.fitted > 0.5, "Dead", "Alive")) %>% 
  select(obs = fate, pred = pred_class)

class_model_pred_2 <- class_model_fit_2 %>% 
  augment(type.predict = "response") %>% 
  mutate(pred_class = ifelse(.fitted > 0.5, "Dead", "Alive")) %>% 
  select(obs = fate, pred = pred_class)

class_model_pred_3 <- class_model_fit_3 %>% 
  augment(type.predict = "response") %>% 
  mutate(pred_class = ifelse(.fitted > 0.5, "Dead", "Alive")) %>% 
  select(obs = fate, pred = pred_class)

Al igual que en el ejercicio anterior, lo que se tendría que hacer una vez que se tienen las predicciones de todos los modelos es juntarlas en una sola tabla:

class_models_predictions <- bind_rows(
  list(
    "model_1" = class_model_pred_1, "model_2" = class_model_pred_2, 
    "model_3" = class_model_pred_3
  ), 
  .id = "model"
)

Como se nos dice en la pista del ejercicio, es necesario antes convertir a las columnas de las clases reales u observadas (obs) y las clases predichas (pred) en factores con el primer nivel como el evento de interés. Dado que nuestro evento de interés es “Alive”, ponemos a esta clase como el primer nivel:

class_models_predictions <- class_models_predictions %>% 
  mutate(
    obs = factor(obs, levels = c("Alive", "Dead")),
    pred = factor(pred, levels = c("Alive", "Dead"))
  )

Ahora, definimos un conjunto de medidas con aquellas solicitadas en el ejercicio y calculamos para cada modelo:

metrics_classification <- metric_set(accuracy, mcc, kap)

class_models_predictions %>% 
  group_by(model) %>%
  metrics_classification(truth = obs, estimate = pred, event_level = "second")
# A tibble: 9 × 4
  model   .metric  .estimator .estimate
  <chr>   <chr>    <chr>          <dbl>
1 model_1 accuracy binary         0.685
2 model_2 accuracy binary         0.692
3 model_3 accuracy binary         0.692
4 model_1 mcc      binary         0.190
5 model_2 mcc      binary         0.227
6 model_3 mcc      binary         0.220
7 model_1 kap      binary         0.164
8 model_2 kap      binary         0.208
9 model_3 kap      binary         0.198

Observamos que el primer modelo (model_1) tiene el peor performance de clasificación según las medidas de evaluación usadas. El segundo (model_2) y tercer (model_3) modelo tienen un performance similar, aunque model_2 tiene un mayor coeficiente de correlación de Matthews y coeficiente kappa e igual exactitud (accuracy) que model_3.

Regresión lineal: Conceptos básicos

Ejercicio 1

Leamos y demos un vistazo a los datos:

iq <- read_csv("data/iq.csv")
Rows: 434 Columns: 5
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (5): kid_score, mom_hs, mom_iq, mom_work, mom_age

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
View(iq)

Los puntajes de los test de IQ para los niños se encuentran en la variable kid_score, mientras que los puntajes de las madres en mom_iq. Para construir el modelo de regresión lineal, usamos la función lm():

regre_simple_iq <- lm(kid_score ~ mom_iq, data = iq)
summary(regre_simple_iq)

Call:
lm(formula = kid_score ~ mom_iq, data = iq)

Residuals:
    Min      1Q  Median      3Q     Max 
-56.753 -12.074   2.217  11.710  47.691 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 25.79978    5.91741    4.36 1.63e-05 ***
mom_iq       0.60997    0.05852   10.42  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 18.27 on 432 degrees of freedom
Multiple R-squared:  0.201, Adjusted R-squared:  0.1991 
F-statistic: 108.6 on 1 and 432 DF,  p-value: < 2.2e-16

Podemos obtener los intervalos del confianza de los parámetros del modelo usando la función confint(). Para un 97% de confianza, agregamos el argumento level = 0.97:

confint(regre_simple_iq, level = 0.97)
                 1.5 %     98.5 %
(Intercept) 12.9158953 38.6836604
mom_iq       0.4825579  0.7373912

Para obtener los resultados en formato tidy, podemos usar la función tidy() del paquete broom con los argumentos conf.int = TRUE y conf.level = 0.97:

tidy(regre_simple_iq, conf.int = TRUE, conf.level = 0.97)
# A tibble: 2 × 7
  term        estimate std.error statistic  p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
1 (Intercept)   25.8      5.92        4.36 1.63e- 5   12.9      38.7  
2 mom_iq         0.610    0.0585     10.4  7.66e-23    0.483     0.737

Interpretación: Tenemos un 97% de confianza de que, en promedio, el puntaje del test de IQ de un niño aumentaría entre 0.48 y 0.74 unidades por un aumento de una unidad en el puntaje de la madre.

Ejercicio 2

La variable mom_hs contiene la variable indicadora de si la madre se graduó (1) o no (0) de la secundaria. Primero, convertimos esta variable en factor:

iq_v2 <- iq %>% 
  mutate(mom_hs = factor(mom_hs, levels = c(0, 1), labels = c("No", "Sí")))

Ahora, construimos el modelo de regresión lineal múltiple:

regre_mult_iq <- lm(kid_score ~ mom_iq + mom_hs, data = iq_v2)
summary(regre_mult_iq)

Call:
lm(formula = kid_score ~ mom_iq + mom_hs, data = iq_v2)

Residuals:
    Min      1Q  Median      3Q     Max 
-52.873 -12.663   2.404  11.356  49.545 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 25.73154    5.87521   4.380 1.49e-05 ***
mom_iq       0.56391    0.06057   9.309  < 2e-16 ***
mom_hsSí     5.95012    2.21181   2.690  0.00742 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 18.14 on 431 degrees of freedom
Multiple R-squared:  0.2141,    Adjusted R-squared:  0.2105 
F-statistic: 58.72 on 2 and 431 DF,  p-value: < 2.2e-16

Por último, obtenemos los intervalos de confianza:

tidy(regre_mult_iq, conf.int = TRUE, conf.level = 0.97)
# A tibble: 3 × 7
  term        estimate std.error statistic  p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
1 (Intercept)   25.7      5.88        4.38 1.49e- 5   12.9      38.5  
2 mom_iq         0.564    0.0606      9.31 6.61e-19    0.432     0.696
3 mom_hsSí       5.95     2.21        2.69 7.42e- 3    1.13     10.8

Intrepretación:

  • Tenemos un 97% de confianza de que, en promedio, el puntaje del test de IQ de un niño aumenta entre 0.43 y 0.70 unidades por un aumento de una unidad en el puntaje de la madre, dado que la madre no cambia su condición de graduada o no graduada de la secundaria.

  • Tenemos un 97% de confianza de que si la madre pasara de no estar graduada de la secundaria a graduada, el puntaje del test de IQ del niño aumentaría, en promedio, entre 1.1343381 y 10.765896 unidades, dado que la madre mantiene su puntaje de IQ.

Ejercicio 3

regre_mult_inter_iq <- lm(kid_score ~ mom_iq + mom_hs + mom_iq*mom_hs, data = iq_v2)
summary(regre_mult_inter_iq)

Call:
lm(formula = kid_score ~ mom_iq + mom_hs + mom_iq * mom_hs, data = iq_v2)

Residuals:
    Min      1Q  Median      3Q     Max 
-52.092 -11.332   2.066  11.663  43.880 

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)     -11.4820    13.7580  -0.835 0.404422    
mom_iq            0.9689     0.1483   6.531 1.84e-10 ***
mom_hsSí         51.2682    15.3376   3.343 0.000902 ***
mom_iq:mom_hsSí  -0.4843     0.1622  -2.985 0.002994 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 17.97 on 430 degrees of freedom
Multiple R-squared:  0.2301,    Adjusted R-squared:  0.2247 
F-statistic: 42.84 on 3 and 430 DF,  p-value: < 2.2e-16

Para obtener los efectos marginales, podemos usar la función estimate_slopes() del paquete modelbased:


Attaching package: 'modelbased'
The following object is masked from 'package:rstatix':

    get_emmeans
The following object is masked from 'package:huxtable':

    print_md
estimate_slopes(regre_mult_inter_iq, trend = "mom_iq", at = "mom_hs")
Estimated Marginal Effects

mom_hs | Coefficient |   SE |       95% CI | t(430) |      p
------------------------------------------------------------
No     |        0.97 | 0.15 | [0.68, 1.26] |   6.53 | < .001
Sí     |        0.48 | 0.07 | [0.36, 0.61] |   7.38 | < .001
Marginal effects estimated for mom_iq

Intrepretación: El aumento promedio en el puntaje del test de IQ de un niño asociado a un aumento en el puntaje del test de IQ de la madre es de 0.97 unidades en el grupo de las madres que no se graduaron de la secundaria, mientras que en el grupo de las madres que sí se graduaron el aumento promedio es de 0.48 unidades.

Regresión lineal: Evaluación y extensiones

Ejercicio 1

Leamos y demos un vistazo a los datos:

iq <- read_csv("data/iq.csv")
Rows: 434 Columns: 5
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (5): kid_score, mom_hs, mom_iq, mom_work, mom_age

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
View(iq)

Los puntajes de los test de IQ para los niños se encuentran en la variable kid_score, los puntajes de las madres en mom_iq, y la variable indicadora de si la madre se graduó o no de la secundaria está dada por mom_hs. Primero, convertimos la variable mom_hs en factor:

iq_v2 <- iq %>% 
  mutate(mom_hs = factor(mom_hs, levels = c(0, 1), labels = c("No", "Sí")))

Ahora, construimos el modelo de regresión múltiple:

regre_mult_iq <- lm(kid_score ~ mom_iq + mom_hs, data = iq_v2)
summary(regre_mult_iq)

Call:
lm(formula = kid_score ~ mom_iq + mom_hs, data = iq_v2)

Residuals:
    Min      1Q  Median      3Q     Max 
-52.873 -12.663   2.404  11.356  49.545 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 25.73154    5.87521   4.380 1.49e-05 ***
mom_iq       0.56391    0.06057   9.309  < 2e-16 ***
mom_hsSí     5.95012    2.21181   2.690  0.00742 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 18.14 on 431 degrees of freedom
Multiple R-squared:  0.2141,    Adjusted R-squared:  0.2105 
F-statistic: 58.72 on 2 and 431 DF,  p-value: < 2.2e-16

Para generar los gráficos de residuales, podemos usar la función autoplot() del paquete ggfortify:

autoplot(regre_mult_iq)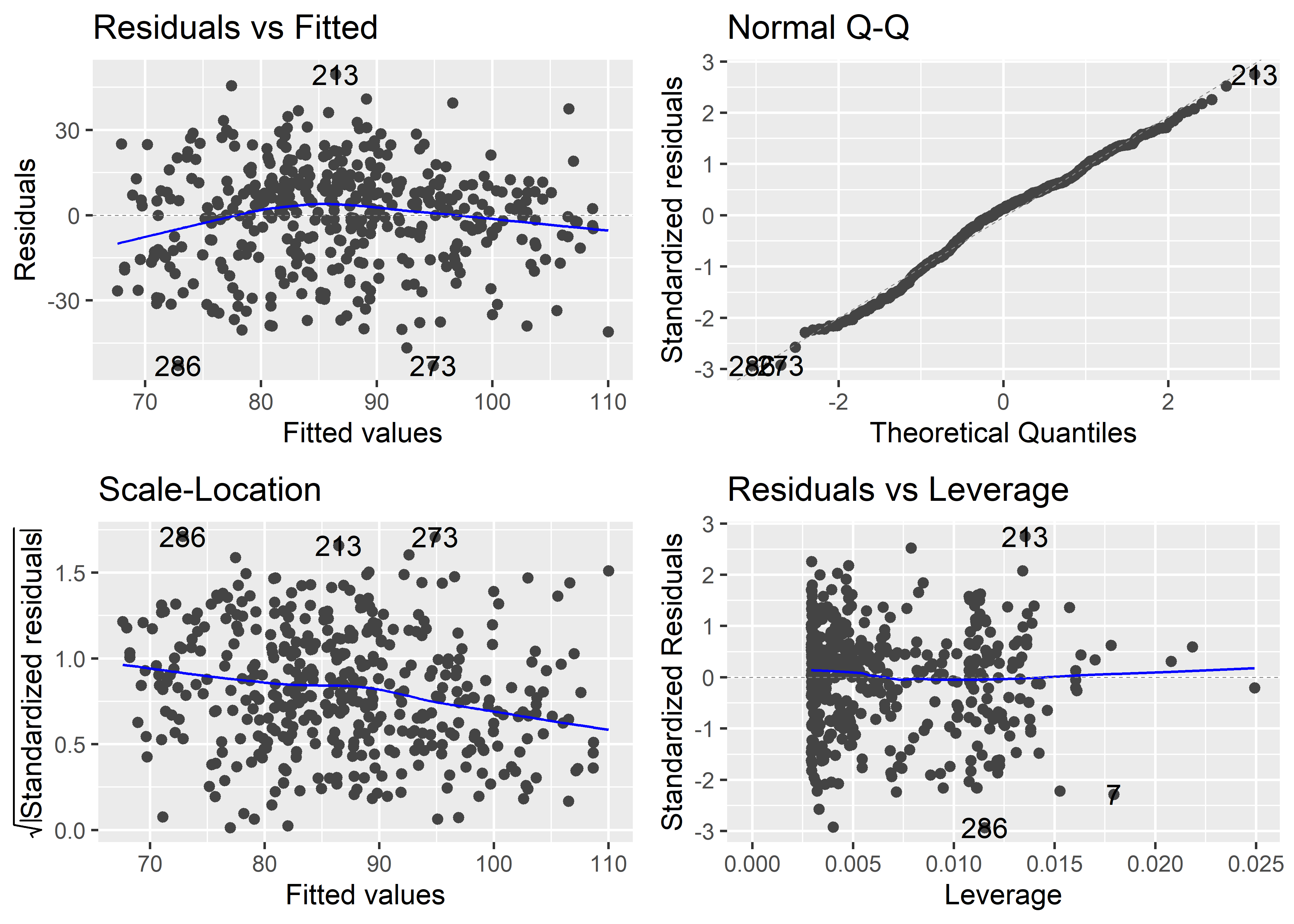

Vemos que, en general, no hay patrones que podrían indicar una falta grave de adecuación del modelo. Las líneas de tendencia en los gráficos “Residuals vs Fitted” y “Scale-location” no son exactamente horizontales, pero tampoco tienen un patrón curvilíneo acentuado. Sin embargo, podría ser buena idea probar añadiendo más predictores o alguna transformación de los predictores actuales para ver si se logra eliminar estos ligeros patrones.

Ejercicio 2

Para añadir una transformación polinómica de grado 2 sobre un predictor usamos la función poly() y pasamos al parámetro degree el valor 2:

regre_mult_poly_iq <- lm(kid_score ~ poly(mom_iq, degree = 2) + mom_hs, data = iq_v2)
summary(regre_mult_poly_iq)

Call:
lm(formula = kid_score ~ poly(mom_iq, degree = 2) + mom_hs, data = iq_v2)

Residuals:
    Min      1Q  Median      3Q     Max 
-54.553 -10.940   2.502  11.095  48.710 

Coefficients:
                          Estimate Std. Error t value Pr(>|t|)    
(Intercept)                 82.784      1.937  42.749   <2e-16 ***
poly(mom_iq, degree = 2)1  178.049     18.733   9.504   <2e-16 ***
poly(mom_iq, degree = 2)2  -55.989     18.096  -3.094   0.0021 ** 
mom_hsSí                     5.107      2.207   2.314   0.0211 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 17.96 on 430 degrees of freedom
Multiple R-squared:  0.2313,    Adjusted R-squared:  0.2259 
F-statistic: 43.12 on 3 and 430 DF,  p-value: < 2.2e-16

Ahora veamos los gráficos de residuales:

autoplot(regre_mult_poly_iq)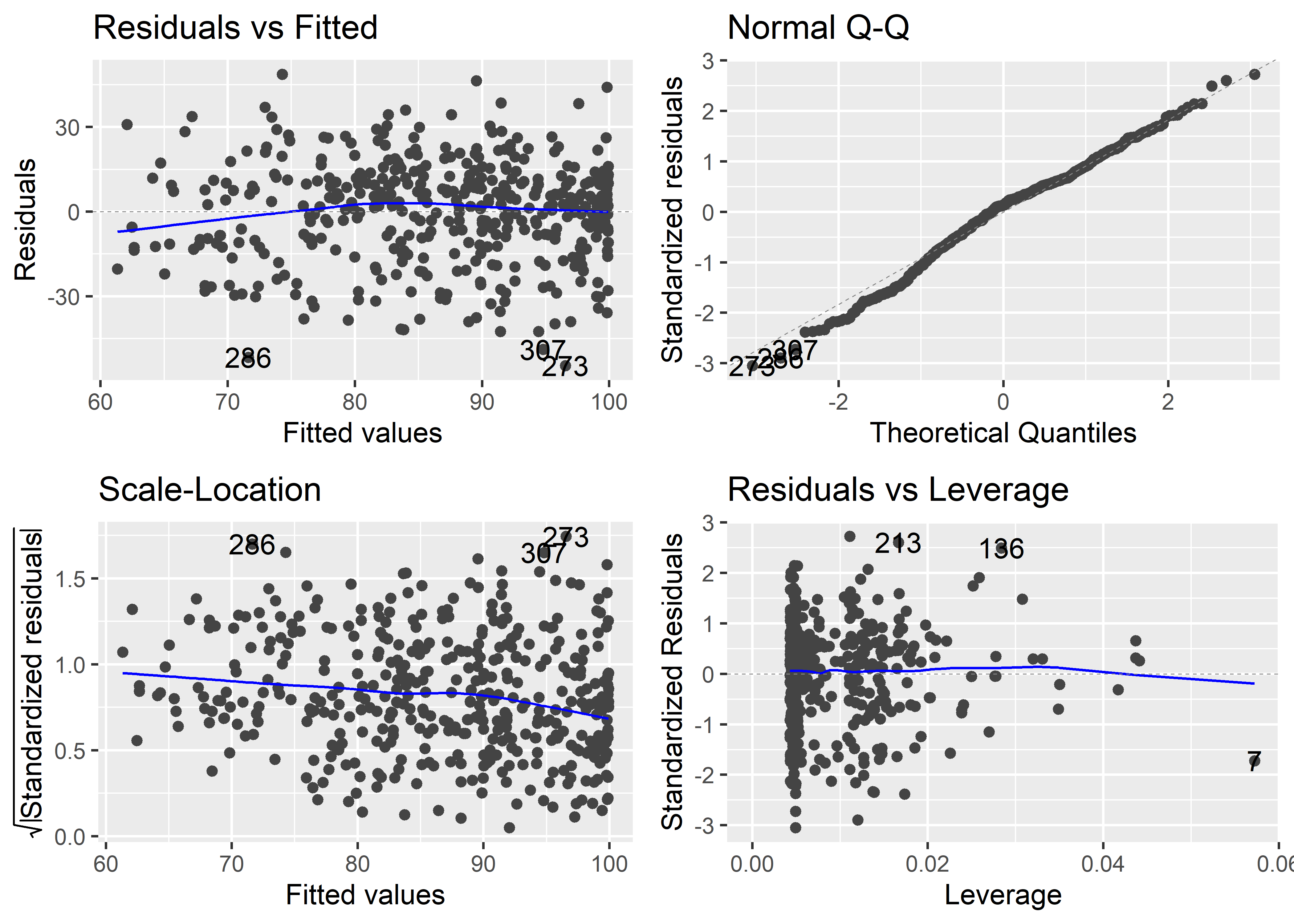

Vemos que con la transformación polinómica sobre mom_iq, las líneas de tendencia en los gráficos “Residuals vs Fitted” y “Scale-location” se hacen más horizontales y los patrones curvilíneos se atenúan. Por lo tanto, este modelo parece ser adecuado para explicar los puntajes de las pruebas de IQ de los niños.

Ejercicio 3

Ajustemos los modelos que se piden:

regre_simple_iq_iq <- lm(kid_score ~ mom_iq, data = iq)
regre_simple_hs_iq <- lm(kid_score ~ mom_hs, data = iq)
regre_multi_iq <- lm(kid_score ~ mom_iq + mom_hs, data = iq)
regre_multi_inter_iq <- lm(kid_score ~ mom_iq + mom_hs + mom_iq*mom_hs, data = iq)

Podemos usar la función compare_performance() del paquete performance para comparar el ajuste de los modelos:


Attaching package: 'performance'
The following objects are masked from 'package:yardstick':

    mae, rmse
The following objects are masked from 'package:huxtable':

    print_html, print_md
compare_performance(
  regre_simple_iq_iq, regre_simple_hs_iq, regre_multi_iq, regre_multi_inter_iq, 
  rank = TRUE
)
# Comparison of Model Performance Indices

Name                 | Model |    R2 | R2 (adj.) |   RMSE |  Sigma | AIC weights | AICc weights | BIC weights | Performance-Score
---------------------------------------------------------------------------------------------------------------------------------
regre_multi_inter_iq |    lm | 0.230 |     0.225 | 17.888 | 17.971 |       0.967 |        0.966 |       0.725 |           100.00%
regre_multi_iq       |    lm | 0.214 |     0.210 | 18.073 | 18.136 |       0.031 |        0.031 |       0.176 |            56.41%
regre_simple_iq_iq   |    lm | 0.201 |     0.199 | 18.224 | 18.266 |       0.002 |        0.002 |       0.099 |            49.89%
regre_simple_hs_iq   |    lm | 0.056 |     0.054 | 19.807 | 19.853 |    4.51e-19 |     4.70e-19 |    1.98e-17 |             0.00%

Considerando todos los indicadores de ajuste, el modelo que incluye la interacción entre el puntaje del test de IQ de la madre y la condición de si la madre se graduó o no de secundaria tiene un ajuste a los datos.

Medidas de frecuencia

Ejercicio 1

library(tidyverse)
library(sampler)
framingham <- read_csv("data/framingham_freq.csv")
  • Prevalencia puntual al incio de estudio de enfermedad coronaria estratificado por diabetes
angina_0_diabetes <- framingham %>%
  filter(TIME == 0) %>%
  mutate(PREVMI = factor(PREVMI, 
                         levels = c(0,1), 
                         labels = c("no", "yes")),
         DIABETES = factor(DIABETES, 
                      levels = c(0,1), 
                      labels = c("No diabetes", "Diabetes"))) %>%
  group_by(DIABETES, PREVMI) %>% 
  summarise(n=n())
`summarise()` has grouped output by 'DIABETES'. You can override using the
`.groups` argument.
angina_0_diabetes
# A tibble: 4 × 3
# Groups:   DIABETES [2]
  DIABETES    PREVMI     n
  <fct>       <fct>  <int>
1 No diabetes no      4234
2 No diabetes yes       79
3 Diabetes    no       114
4 Diabetes    yes        7
angina_0_diabetes %>%
  group_by(DIABETES) %>% 
  rpro(n, ci = 95)
Adding missing grouping variables: `DIABETES`
Storing counts in `nn`, as `n` already present in input
# A tibble: 4 × 6
# Groups:   DIABETES [2]
  DIABETES        n midpoint    me lower upper
  <fct>       <int>    <dbl> <dbl> <dbl> <dbl>
1 No diabetes    79     1.83 0.400  1.43  2.23
2 No diabetes  4234    98.2  0.400 97.8  98.6 
3 Diabetes        7     5.79 4.18   1.61  9.96
4 Diabetes      114    94.2  4.18  90.0  98.4

En la población de Framingham, la prevalencia puntual al incio del estudio de infarto al miocardio en población diabética es 4.18 (IC95%: 90.04 - 98.39).

Ejercicio 2

  • Prevalencia de hipertensión en el periodo 2
#Seleccionando el periodo 2 
pp_hipertension <- framingham %>%
  mutate(hipertension = PREVHYP + HYPERTEN) %>% 
  mutate(hipertension = case_when(hipertension >= 1 ~ 1,
                            TRUE ~ 0)) %>% 
  mutate(hipertension = factor(hipertension, 
                         levels = c(0,1), 
                         labels = c("No hipertensión", "Hipertensión"))) 

hipertension_p2 <- pp_hipertension %>% 
  filter(PERIOD == 2) %>%  
  group_by(hipertension) %>% 
  summarise(n = n())

hipertension_p2 %>%
  rpro(n, ci = 95)
Storing counts in `nn`, as `n` already present in input
ℹ Use `name = "new_name"` to pick a new name.
# A tibble: 2 × 5
      n midpoint    me lower upper
  <int>    <dbl> <dbl> <dbl> <dbl>
1   995     25.3  1.36  24.0  26.7
2  2936     74.7  1.36  73.3  76.0

En la población de Framingham, la prevalencia de hipertensión en el segundo periodo de estudio 1.36 (IC95%: 73.33 - 76.05).

Ejercicio 3

  • Incidencia de stroke en el periodo 3
free_prev_stroke <- framingham %>% 
  filter(PREVSTRK == 0 & PERIOD == 3) %>%
  mutate(STROKE = factor(STROKE, 
                           levels = c(0,1), 
                           labels = c("No stroke ", "Stroke"))) 

stroke <- free_prev_stroke %>% 
  group_by(STROKE) %>% 
  count()

stroke %>%
  ungroup() %>% 
  rpro(n, ci = 95)
Storing counts in `nn`, as `n` already present in input
ℹ Use `name = "new_name"` to pick a new name.
# A tibble: 2 × 5
      n midpoint    me lower upper
  <int>    <dbl> <dbl> <dbl> <dbl>
1   214     6.70 0.867  5.83  7.57
2  2980    93.3  0.867 92.4  94.2

Durante el periodo 3 del estudio de Framingham, se observó una incidencia acumulada del 6.7% (IC 95%: 5.83 - 7.57) . Es decir, por cada 1000 personas, hubo aproximadamente 67 casos nuevos de stroke.

Medidas de asociación

library(tidyverse)
library(epiR)
library(fmsb)
framingham <- read.csv("./data/framingham_freq.csv")

Ejercicio 1

Calculando la Razón de prevalencia de PREVCHD al basal respecto al factor de exposición de sexo:

prevalence_chd <- framingham %>% 
  filter(TIME==0) %>% 
  select(PREVCHD, SEX) %>% 
  mutate(PREVCHD = factor(PREVCHD, 
                         levels = c(1,0), 
                         labels = c("Enfermedad cardicaca", "No enfermedad cardiaca")),
         SEX = factor(SEX, levels = c(1,2), 
                      labels = c("Male", "Female")))

tab_prevalence <- table(prevalence_chd$SEX, prevalence_chd$PREVCHD)

tab_prevalence
        
         Enfermedad cardicaca No enfermedad cardiaca
  Male                    124                   1820
  Female                   70                   2420
epi.2by2(tab_prevalence, method = "cross.sectional")
             Outcome +    Outcome -      Total               Prev risk *
Exposed +          124         1820       1944       6.38 (5.33 to 7.56)
Exposed -           70         2420       2490       2.81 (2.20 to 3.54)
Total              194         4240       4434       4.38 (3.79 to 5.02)

Point estimates and 95% CIs:
-------------------------------------------------------------------
Prev risk ratio                                2.27 (1.70, 3.02)
Prev odds ratio                                2.36 (1.75, 3.18)
Attrib prev in the exposed *                   3.57 (2.30, 4.83)
Attrib fraction in the exposed (%)            55.93 (41.28, 66.92)
Attrib prev in the population *                1.56 (0.68, 2.45)
Attrib fraction in the population (%)         35.75 (22.78, 46.53)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 33.206 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
 Wald confidence limits
 CI: confidence interval
 * Outcomes per 100 population units

En la población de Framingham, la prevalencia de cardiopatía coronaria en las mujeres es 2.27 (IC95%: 1.70 - 3.02) veces la prevalencia en el grupo de los hombres.

Calculando la Razón de Odds de PREVCHD al basal respecto al factor de exposición de condición de fumador:

odds_chd <- framingham %>% 
  filter(TIME==0) %>% 
  select(PREVCHD, CURSMOKE) %>% 
  mutate(PREVCHD = factor(PREVCHD, 
                           levels = c(1,0), 
                           labels = c("Enfermedad cardicaca", "No enfermedad cardiaca")),
         CURSMOKE = factor(CURSMOKE, 
                           levels = c(1,0), 
                           labels = c("Fumador","No Fumador")))

odds_tab <- table(odds_chd$CURSMOKE, odds_chd$PREVCHD)

odds_tab
            
             Enfermedad cardicaca No enfermedad cardiaca
  Fumador                      86                   2095
  No Fumador                  108                   2145
epi.2by2(odds_tab, method = "case.control")
             Outcome +    Outcome -      Total                       Odds
Exposed +           86         2095       2181        0.04 (0.03 to 0.05)
Exposed -          108         2145       2253        0.05 (0.04 to 0.06)
Total              194         4240       4434        0.05 (0.04 to 0.05)

Point estimates and 95% CIs:
-------------------------------------------------------------------
Exposure odds ratio                            0.82 (0.61, 1.09)
Attrib fraction (est) in the exposed (%)      -22.65 (-65.86, 9.08)
Attrib fraction (est) in the population (%)   -10.04 (-25.20, 3.28)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 1.916 Pr>chi2 = 0.166
Fisher exact test that OR = 1: Pr>chi2 = 0.186
 Wald confidence limits
 CI: confidence interval

En la población de Framingham, el Odds de cardiopatía coronaria en el grupo de fumadores es 0.82 (IC95%: 0.61 - 1.09) veces el Odds en el grupo de no fumadores. Como se puede observar, el intervalo de confianza contiene a la unidad, por tal motivo, este resultado no es estadísticamente significativo.

Calculando la Razón de Odds de PREVCHD en el periodo 2 respecto al factor de exposición de diabetes:

incident_chd <- framingham %>% 
  filter(PREVCHD == 0 & PERIOD == 2) %>%
  select(ANYCHD, DIABETES) %>% 
  mutate(ANYCHD = factor(ANYCHD, 
                           levels = c(1,0), 
                           labels = c("Enfermedad cardicac", "No enfermedad cardiaca")),
         DIABETES = factor(DIABETES, 
                           levels = c(1,0), 
                           labels = c("Diabetico", "No diabetico")))


tab_incience <- table(incident_chd$DIABETES, incident_chd$ANYCHD)

tab_incience
              
               Enfermedad cardicac No enfermedad cardiaca
  Diabetico                     62                     62
  No diabetico                 721                   2797
epi.2by2(tab_incience, method = "cohort.count")
             Outcome +    Outcome -      Total                 Inc risk *
Exposed +           62           62        124     50.00 (40.89 to 59.11)
Exposed -          721         2797       3518     20.49 (19.17 to 21.87)
Total              783         2859       3642     21.50 (20.17 to 22.87)

Point estimates and 95% CIs:
-------------------------------------------------------------------
Inc risk ratio                                 2.44 (2.02, 2.94)
Inc odds ratio                                 3.88 (2.70, 5.57)
Attrib risk in the exposed *                   29.51 (20.60, 38.41)
Attrib fraction in the exposed (%)            59.01 (50.55, 66.02)
Attrib risk in the population *                1.00 (-0.88, 2.89)
Attrib fraction in the population (%)         4.67 (3.05, 6.27)
-------------------------------------------------------------------
Uncorrected chi2 test that OR = 1: chi2(1) = 61.785 Pr>chi2 = <0.001
Fisher exact test that OR = 1: Pr>chi2 = <0.001
 Wald confidence limits
 CI: confidence interval
 * Outcomes per 100 population units

En la población de Framingham, la incidencia de cardiopatía coronaria en el grupo de diabéticos es 2.44 (IC95%: 2.02 - 2.94) veces la incidencia en el grupo de no fumadores.

Ejercicio 2

Razón de tasa de incidencias para la variable Enfermedad Coronaria (ANYCHD) en función de la condición de diabetes. Hacer el cálculo para el segundo periodo de estudio.

rti_chd <- framingham %>% 
  filter(PREVCHD == 0 & PERIOD == 2) %>%
  select(ANYCHD, DIABETES, TIMECHD) %>% 
  mutate(ANYCHD = factor(ANYCHD, 
                           levels = c(1,0), 
                           labels = c("Enfermedad cardicaca", "No enfermedad cardiaca")),
         DIABETES = factor(DIABETES, 
                           levels = c(1,0), 
                           labels = c("Diabetico", "No diabetico"))) %>% 
  filter(ANYCHD == "Enfermedad cardicaca") %>% 
  group_by(DIABETES, ANYCHD) %>% 
  summarise(personas_tiempo = sum(TIMECHD),
            cases = n()) %>% 
  select(-ANYCHD) %>% 
  relocate(cases, .after = DIABETES)
`summarise()` has grouped output by 'DIABETES'. You can override using the
`.groups` argument.
rti_chd
# A tibble: 2 × 3
# Groups:   DIABETES [2]
  DIABETES     cases personas_tiempo
  <fct>        <int>           <int>
1 Diabetico       62          314764
2 No diabetico   721         3988907
rti_final <- rateratio(rti_chd$cases[1], rti_chd$cases[2],
                       rti_chd$personas_tiempo[1], rti_chd$personas_tiempo[2],
                       conf.level = 0.95)
            Cases Person-time
Exposed        62      314764
Unexposed     721     3988907
Total         783     4303671
str(rti_final)
List of 5
 $ p.value  : num 0.516
 $ conf.int : num [1:2] 0.841 1.412
  ..- attr(*, "conf.level")= num 0.95
 $ estimate : num 1.09
 $ method   : chr "Incidence rate ratio estimate and its significance probability"
 $ data.name: chr "rti_chd$cases[1] rti_chd$cases[2] rti_chd$personas_tiempo[1] rti_chd$personas_tiempo[2]"
 - attr(*, "class")= chr "htest"
print(rti_final)

    Incidence rate ratio estimate and its significance probability

data:  rti_chd$cases[1] rti_chd$cases[2] rti_chd$personas_tiempo[1] rti_chd$personas_tiempo[2]
p-value = 0.516
95 percent confidence interval:
 0.8407569 1.4124728
sample estimates:
[1] 1.089746

En la población de Framingham, la tasa de incidencia de enfermedad coronaria en el grupo de diabéticos es 1.09 (IC95%: 0.84 - 1.41) veces la tasa de incidencia en el grupo de no diabéticos.

Estudios Transversales

library(jtools)
library(broom)
covid_mex <- read_csv("data/covid_mexico_2.csv")

Ejercicio 1

Elabore un modelo de regresión logístico incluyendo a la condición de UCI (UCI) como outcome y solo a las variables Sexo (SEX) y la condición de fumador (TABAQUISMO) como predictores. Exponencie los coeficientes de la regresión para obtener los OR.

Para ello, factorizaremos las variables que serán utilizadas en el análisis.

covid_mex_clean_1 <- covid_mex %>% 
  mutate(
    SEXO = case_when(
      SEXO == 1 ~ 1,
      TRUE ~ 0
    ),
    TABAQUISMO = factor(
      TABAQUISMO,
      levels = c(0, 1),
      labels = c("No Fumador", "Fumador")
      ),
    SEXO = factor(
      SEXO,
      levels = c(0, 1),
      labels = c("Femenino", "Masculino")
      ),
    UCI = factor(
      UCI,
      levels = c(0,1),
      labels = c("No UCI", "UCI")
    )
  )

Posteriormente, se ejecutará el modelo de regresión logística

log_reg_eje_1 <- glm(
  UCI ~ SEXO + TABAQUISMO,
  family = binomial(link = "logit"),
  data = covid_mex_clean_1
  )

Finalmente, se deben exponenciar los coeficientes para poder obtener el OR.

exponenciado_logistica <- log_reg_eje_1 %>% 
  tidy(exponentiate = TRUE, conf.int = TRUE)

exponenciado_logistica
# A tibble: 3 × 7
  term              estimate std.error statistic   p.value conf.low conf.high
  <chr>                <dbl>     <dbl>     <dbl>     <dbl>    <dbl>     <dbl>
1 (Intercept)         0.0722     0.104    -25.3  6.42e-141   0.0585    0.0880
2 SEXOMasculino       0.753      0.177     -1.60 1.09e-  1   0.529     1.06  
3 TABAQUISMOFumador   1.30       0.257      1.01 3.15e-  1   0.760     2.09

En la población de pacientes mexicanos con COVID-19, El Odds de ingresar a UCI en el grupo de hombres es 0.75 (IC95%: 0.53 - 1.06) veces el Odds en el grupo de mujeres, luego de ajustar por la condición de fumador. Este resultado no fue estadísticamente significativo (p=0.109).

Ejercicio 2

Elabore un modelo de regresión de Poisson Modificado incluyendo a la condición de UCI (UCI) como outcome y solo a las variables obesidad (OBESIDAD) y la condición de asma (ASMA) como predictores. Exponencie los coeficientes de la regresión para obtener los OR.

Al igual que en el ejercicio anterior, deberemos convertir en factor las variables que serán utilizadas en nuestro análisis.

covid_mex_clean_2 <- covid_mex %>% 
  mutate(
    OBESIDAD = factor(
      OBESIDAD,
      levels = c(0, 1),
      labels = c("No Obeso", "Obeso")
      ),
    ASMA = factor(
      ASMA,
      levels = c(0, 1),
      labels = c("Asmatico", "No Asmatico")
      )
    )

Posteriormente, se ejecutará el modelo de regresión de Poisson

poisson_eje_2 <- glm(
  UCI ~ OBESIDAD + ASMA,
  family = poisson(link="log"),
  data = covid_mex_clean_2
)

poisson_eje_2

Call:  glm(formula = UCI ~ OBESIDAD + ASMA, family = poisson(link = "log"), 
    data = covid_mex_clean_2)

Coefficients:
    (Intercept)    OBESIDADObeso  ASMANo Asmatico  
        -2.8826           0.3812           0.4839  

Degrees of Freedom: 2599 Total (i.e. Null);  2597 Residual
Null Deviance:      906.4 
Residual Deviance: 899.8    AIC: 1234

Ahora estimaremos la varianza robusta y exponenciaremos los coeficientes.

model_poisson_mod_exp <- summ(poisson_eje_2, robust = "HC1", confint = T, digits = 3, exp = T)

model_poisson_mod_exp
Observations 2600
Dependent variable UCI
Type Generalized linear model
Family poisson
Link log
χ²(2) 6.557
Pseudo-R² (Cragg-Uhler) 0.007
Pseudo-R² (McFadden) 0.005
AIC 1233.839
BIC 1251.429
exp(Est.) 2.5% 97.5% z val. p
(Intercept) 0.056 0.047 0.067 -31.203 0.000
OBESIDADObeso 1.464 1.065 2.013 2.348 0.019
ASMANo Asmatico 1.622 0.795 3.310 1.330 0.184
Standard errors: Robust, type = HC1

En la población de pacientes mexicanos con COVID-19, la proporción de personas que ingresan a UCI en el grupo de obesos es 1.46 (IC95%: 1.07 - 2.01) veces la proporción en el grupo de no obesos, luego de ajustar por la condición de asma Este resultado fue estadísticamente significativo con un valor p = 0.019.

Estudios de Casos y Controles

Ejercicio 1

A) Usando la base de datos peru (dhs.csv), realizar un emparejamiento individual en base a la provincia, grupo de riqueza y quintil de edad. Utilizar una proporción fija. Es decir, incluir solo a los casos que se hayan podido emparejar 3 controles.

library(tidyverse)
library(MatchIt)
library(survival)
library(broom)

peru <- read_csv("data/dhs.csv")

peru <- peru %>%
  drop_na() %>%
  mutate(province = str_sub(village, 1, 2),
         safe_water = factor(safe_water, labels = c("No", "Si")),
         age_cat = cut_number(age, 5))

peru_match <- matchit(death_1m ~ province + wealth_ind + age_cat, 
          exact = ~ province + wealth_ind + age_cat, 
          ratio = 3, 
          data = peru)

dat_m <- match.data(peru_match)

dat_m <- dat_m %>%
  group_by(subclass) %>%
  filter(n() > 3) %>%
  ungroup()

logit2 <- clogit(death_1m ~ safe_water + strata(subclass), data = dat_m)

tidy(logit2, exponentiate = T, conf.int = T)
# A tibble: 1 × 7
  term         estimate std.error statistic p.value conf.low conf.high
  <chr>           <dbl>     <dbl>     <dbl>   <dbl>    <dbl>     <dbl>
1 safe_waterSi    0.498     0.386     -1.81  0.0707    0.234      1.06

B) Comparar los resultados con el emparejamiento individual con proporción fija.

Estudios de cohortes

library(tidyverse)
library(broom)
library(ggplot2)
library(sjPlot)

framingham <- read_csv("data/framingham_cohort_dataset.csv")

Ejercicio 1

Realizar un modelo de regresión de Poisson para estimar tasas individuales, considerando como desenlace a la variable casos de hipertensión (HYPERTEN) y como covariables a edad (AGE), número de cigarrillos por día (CIGPDAY) e índice de masa corporal (BMI).

Recordemos que en un estudio de cohortes se iniciará el análisis con casos incidentes (casos nuevos). Para ello, manipularemos la base de datos para obtener los casos nuevos de hipertensión.

libre_hipertension <- framingham %>%
 mutate( 
  PREVHYP = factor(PREVHYP,
                          levels = c(0, 1),
                          labels = c("No hipertenso", "Hipertenso Prevalente"))
  ) %>% 
 filter(PREVHYP != "Hipertenso Prevalente")

Utilizaremos el comando slice_tail() para obtener el último registro de cada participante en la base de datos.

casos_hipertension <- libre_hipertension %>% 
  arrange(PERIOD) %>% 
  group_by(RANDID) %>% 
  slice_tail(n = 1)

A continuación ejecutaremos el modelo de regresión de Poisson.

poisson_hipertension <- glm(HYPERTEN ~  AGE + CIGPDAY + BMI,
               family = poisson(link="log"),
               data = casos_hipertension)

poisson_hipertension_tidy <- tidy(poisson_hipertension, conf.int = T, exponentiate = T)

poisson_hipertension_tidy
# A tibble: 4 × 7
  term        estimate std.error statistic      p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>        <dbl>    <dbl>     <dbl>
1 (Intercept)    0.546   0.237       -2.55 0.0107          0.343     0.869
2 AGE            0.987   0.00281     -4.79 0.00000171      0.981     0.992
3 CIGPDAY        0.996   0.00197     -2.11 0.0349          0.992     1.00 
4 BMI            1.03    0.00633      5.40 0.0000000659    1.02      1.05

En la población de estudio, la incidencia acumulada de hipertensión arterial es 0.987 (IC95%: 0.981 - 0.992) cuando la edad incrementa en una unidad, ajustando por cigarrillos por día e índice de masa corporal. Siendo este resultado estadísticamente significativo (p < 0.001).

Ejercicio 2

Considerando las variables del modelo del ejercicio 1, calcule las tasas agrupadas por periodo (PERIOD) y sexo (SEX).

casos_hipertension_agrupado <- casos_hipertension %>% 
  group_by(PERIOD, SEX) %>% 
  summarise(casos_hipertension = sum(HYPERTEN, na.rm = T),
            AGE = mean(AGE, na.rm = T),
            BMI = mean(BMI, na.rm = T),
            CIGPDAY = mean(CIGPDAY, na.rm = T)
            )
`summarise()` has grouped output by 'PERIOD'. You can override using the
`.groups` argument.
modelo_hipertension_agrupado <- glm(casos_hipertension ~ AGE + CIGPDAY + BMI + SEX,
               family = poisson(link="log"),
               data = casos_hipertension_agrupado)

modelo_hipertension_tidy <- tidy(modelo_hipertension_agrupado, conf.int = T, exponentiate = T)

En la población de estudio, la incidencia acumulada de hipertensión arterial es 0.802 (IC95%: 0.655 - 0.981) cuando la edad incrementa en una unidad, ajustando por consumo de cigarillo por día, índice de masa corporal y sexo. Siendo este resultado estadísticamente significativo (p=0.032).

Estudios de supervivencia

Para este ejercicio, procedemos con la creación de la variable edad dicotomizada (<= 70 años y > 70 años), para su posterior factorización.

data_cancer <- cancer %>% 
  mutate(
  status = case_when(status == 2 ~ 1,
                       status == 1 ~ 0,
                       TRUE ~ status),
  edad_cat = case_when(age <= 70 ~ 0,
                        TRUE ~ 1),
  edad_cat = factor(edad_cat,
                   levels = c(0,1),
                   labels = c("Menor o igual a 70 años", "Mayor de 70 años"))
  )

Con la base de datos preparada, realizaremos el análisis de supervivencia utilizando el método de Kaplan-Meier.

km_ecog_curve <- survfit(Surv(time, status) ~ edad_cat, data=data_cancer)

tidy(km_ecog_curve)
# A tibble: 201 × 9
    time n.risk n.event n.censor estimate std.error conf.high conf.low strata   
   <dbl>  <dbl>   <dbl>    <dbl>    <dbl>     <dbl>     <dbl>    <dbl> <chr>    
 1     5    182       1        0    0.995   0.00551     1        0.984 edad_cat…
 2    11    181       1        0    0.989   0.00781     1        0.974 edad_cat…
 3    13    180       1        0    0.984   0.00960     1        0.965 edad_cat…
 4    15    179       1        0    0.978   0.0111      1.00     0.957 edad_cat…
 5    53    178       2        0    0.967   0.0137      0.993    0.941 edad_cat…
 6    60    176       2        0    0.956   0.0159      0.986    0.927 edad_cat…
 7    61    174       1        0    0.951   0.0169      0.983    0.920 edad_cat…
 8    62    173       1        0    0.945   0.0179      0.979    0.913 edad_cat…
 9    65    172       2        0    0.934   0.0197      0.971    0.899 edad_cat…
10    71    170       1        0    0.929   0.0206      0.967    0.892 edad_cat…
# ℹ 191 more rows

En el tiempo 15 del estudio, observamos que la supervivencia es de 97.80% (95%CI: 95.70% - 99.96%) en el grupo de personas que tienen 70 años o menos.

En el tiempo 13 del estudio, observamos que la supervivencia es de 91.30% (95%CI: 83.51% - 99.82%) en el grupo de personas que tienen más de 70 años.

Ejercicio 2

Para el gráfico de Kaplan-Meier estratificado utilizaremos la función autoplot().

autoplot(km_ecog_curve, surv.alpha = 0.8, conf.int.alpha = 0.4) +
  labs(x = "Tiempo", 
       y = "Función de Supervivencia",
       title = "Supervivencia de pacientes \n con cancer de pulmón avanzado") +
  scale_fill_lancet() +
  scale_color_lancet() +
  theme_minimal()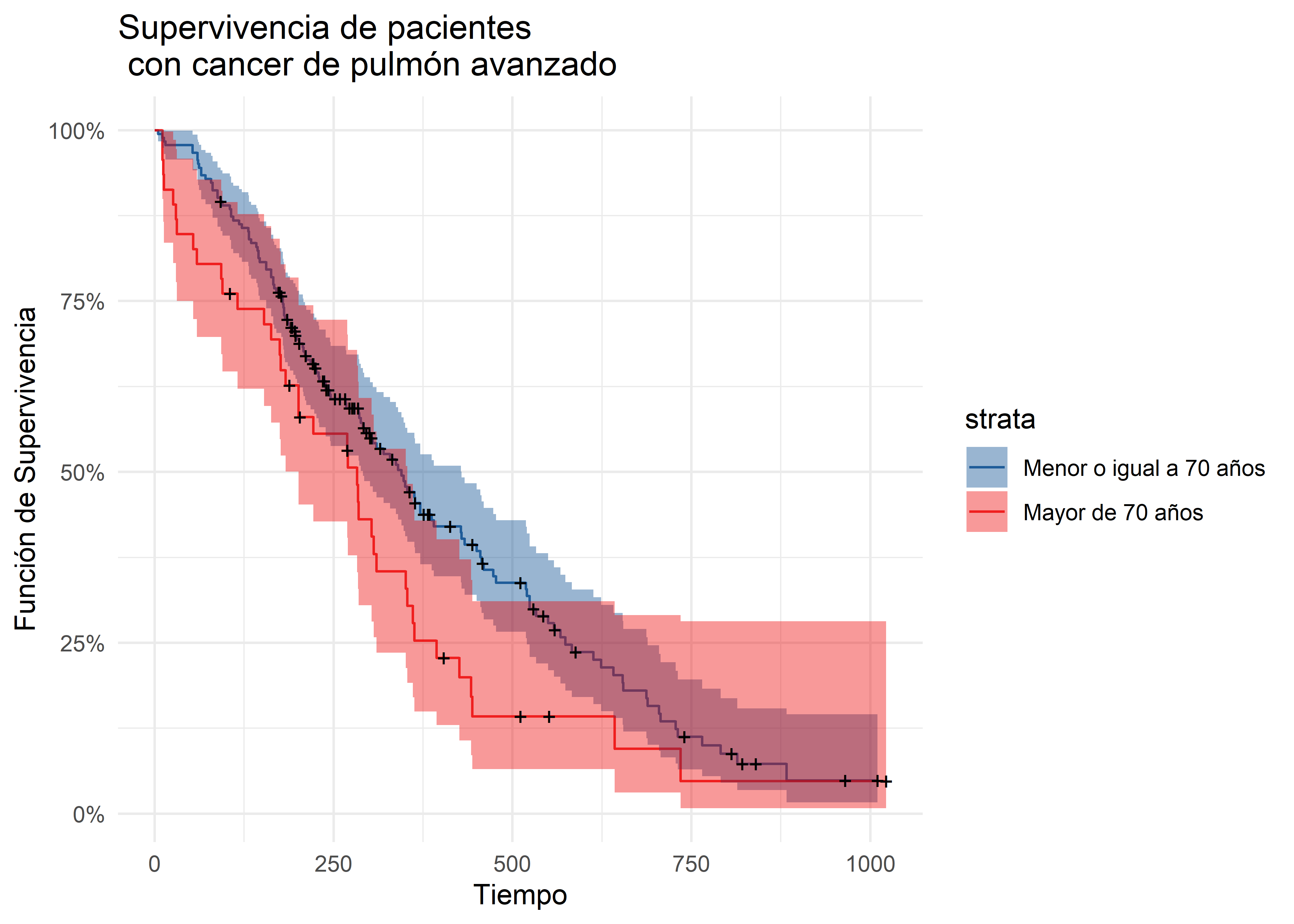

En el gráfico de Kaplan-Meier observamos los pacientes menores o iguales a 70 años llegan al 50% de supervivencia en el día 340, mientras que para el grupo de pacientes mayores a 70 años, el mismo valor de supervivenvia fue observado en el día 270.

Análisis multinivel

Ejercicio 1

Leamos y demos un vistazo a los datos:

nurses <- read_csv("data/nurses.csv")
Rows: 1000 Columns: 11
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (11): hospital, ward, wardid, nurse, age, gender, experien, stress, ward...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
View(nurses)

Primero, transformemos las variables indicadoras en factores:

nurses <- nurses %>% 
  mutate(across(c(hospital:nurse, gender, wardtype, expcon), factor))

Para construir los modelos multinivel, carguemos el paquete lme4:

Loading required package: Matrix

Attaching package: 'Matrix'
The following objects are masked from 'package:pracma':

    expm, lu, tril, triu
The following objects are masked from 'package:tidyr':

    expand, pack, unpack

Attaching package: 'lme4'
The following object is masked from 'package:nlme':

    lmList

Ajustemos el primer modelo con efectos aleatorios correlacionados para los coeficientes de expcon y wardype:

model_v1 <- lmer(
  stress ~ age + gender + experien + expcon + wardtype + (expcon + wardtype|wardid), 
  data = nurses
)
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 1 negative eigenvalues
summary(model_v1)
Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ age + gender + experien + expcon + wardtype + (expcon +  
    wardtype | wardid)
   Data: nurses

REML criterion at convergence: 1644.2

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.75297 -0.70472 -0.00538  0.65276  2.80266 

Random effects:
 Groups   Name        Variance Std.Dev. Corr       
 wardid   (Intercept) 0.2544   0.5043              
          expcon1     0.6708   0.8190    0.14      
          wardtype1   0.4295   0.6554   -0.72 -0.31
 Residual             0.2174   0.4662              
Number of obs: 1000, groups:  wardid, 100

Fixed effects:
             Estimate Std. Error t value
(Intercept)  5.762313   0.115759  49.778
age          0.022162   0.002199  10.078
gender1     -0.453350   0.034987 -12.958
experien    -0.061755   0.004474 -13.804
expcon1     -0.695213   0.147271  -4.721
wardtype1    0.040844   0.125188   0.326

Correlation of Fixed Effects:
          (Intr) age    gendr1 expern expcn1
age       -0.276                            
gender1   -0.225 -0.015                     
experien   0.000 -0.817  0.029              
expcon1   -0.266  0.003 -0.002  0.001       
wardtype1 -0.591 -0.002 -0.004  0.002 -0.051
optimizer (nloptwrap) convergence code: 0 (OK)
unable to evaluate scaled gradient
Model failed to converge: degenerate  Hessian with 1 negative eigenvalues

Vemos que el modelo ha fallado en converger. Usemos la función allFit() para encontrar el optimizador que logre la convergencia y la función glance() del paquete broom.mixed para mostrar los resultados en una tabla:

model_v1_allfit <- allFit(model_v1, verbose = FALSE)
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 1 negative eigenvalues
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 2 negative eigenvalues
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 1 negative eigenvalues
glance(model_v1_allfit)
# A tibble: 5 × 9
  optimizer          nobs sigma logLik   AIC   BIC REMLcrit df.residual  NLL_rel
  <chr>             <int> <dbl>  <dbl> <dbl> <dbl>    <dbl>       <int>    <dbl>
1 bobyqa             1000 0.466  -822. 1670. 1734.    1644.         987 0       
2 Nelder_Mead        1000 0.466  -822. 1670. 1734.    1644.         987 9.66e-12
3 nlminbwrap         1000 0.466  -822. 1670. 1734.    1644.         987 7.50e-12
4 nloptwrap.NLOPT_…  1000 0.466  -822. 1670. 1734.    1644.         987 6.90e- 9
5 nloptwrap.NLOPT_…  1000 0.466  -822. 1670. 1734.    1644.         987 7.00e- 9

Vemos que con el optimizador bobyqa se logra la convergencia (NLL_rel igual a 0). Reajustemos el modelo:

model_v1 <- lmer(
  stress ~ age + gender + experien + expcon + wardtype + (expcon + wardtype|wardid),
  data = nurses, control = lmerControl(optimizer = "bobyqa")
)
summary(model_v1)
Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ age + gender + experien + expcon + wardtype + (expcon +  
    wardtype | wardid)
   Data: nurses
Control: lmerControl(optimizer = "bobyqa")

REML criterion at convergence: 1644.2

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.75297 -0.70472 -0.00538  0.65276  2.80266 

Random effects:
 Groups   Name        Variance Std.Dev. Corr       
 wardid   (Intercept) 0.2544   0.5043              
          expcon1     0.7575   0.8704    0.03      
          wardtype1   0.1677   0.4095   -0.52 -0.46
 Residual             0.2174   0.4662              
Number of obs: 1000, groups:  wardid, 100

Fixed effects:
             Estimate Std. Error t value
(Intercept)  5.762313   0.115759  49.778
age          0.022161   0.002199  10.078
gender1     -0.453350   0.034987 -12.958
experien    -0.061755   0.004474 -13.804
expcon1     -0.695213   0.147271  -4.721
wardtype1    0.040844   0.125189   0.326

Correlation of Fixed Effects:
          (Intr) age    gendr1 expern expcn1
age       -0.276                            
gender1   -0.225 -0.015                     
experien   0.000 -0.817  0.029              
expcon1   -0.266  0.003 -0.002  0.001       
wardtype1 -0.591 -0.002 -0.004  0.002 -0.051

Para evaluar la significancia del modelo,

set.seed(2024)
tidy(model_v1, conf.int = TRUE, conf.method = "boot", boot.type = "perc")
Computing bootstrap confidence intervals ...

4 message(s): boundary (singular) fit: see help('isSingular')
510 warning(s): Hessian is numerically singular: parameters are not uniquely determined (and others)
Computing bootstrap confidence intervals ...

6 message(s): boundary (singular) fit: see help('isSingular')
539 warning(s): Hessian is numerically singular: parameters are not uniquely determined (and others)
# A tibble: 13 × 8
   effect   group    term        estimate std.error statistic conf.low conf.high
   <chr>    <chr>    <chr>          <dbl>     <dbl>     <dbl>    <dbl>     <dbl>
 1 fixed    <NA>     (Intercept)   5.76     0.116      49.8     5.57      5.99  
 2 fixed    <NA>     age           0.0222   0.00220    10.1     0.0182    0.0269
 3 fixed    <NA>     gender1      -0.453    0.0350    -13.0    -0.520    -0.387 
 4 fixed    <NA>     experien     -0.0618   0.00447   -13.8    -0.0715   -0.0529
 5 fixed    <NA>     expcon1      -0.695    0.147      -4.72   -0.964    -0.384 
 6 fixed    <NA>     wardtype1     0.0408   0.125       0.326  -0.231     0.269 
 7 ran_pars wardid   sd__(Inter…   0.504   NA          NA       0.345     0.668 
 8 ran_pars wardid   cor__(Inte…   0.0293  NA          NA      -0.339     0.349 
 9 ran_pars wardid   cor__(Inte…  -0.521   NA          NA      -0.833    -0.0806
10 ran_pars wardid   sd__expcon1   0.870   NA          NA       0.644     1.13  
11 ran_pars wardid   cor__expco…  -0.460   NA          NA      -0.889     0.575 
12 ran_pars wardid   sd__wardty…   0.410   NA          NA       0.281     0.708 
13 ran_pars Residual sd__Observ…   0.466   NA          NA       0.444     0.486

Utilizando el método Bootstrap, vemos que los efectos aleatorios de expcon y wardtype son significativos, dado que los intervalos de confianza no contienen el 0.

Ajustemos ahora el segundo modelo con efectos aleatorios no correlacionados para expcon y wardtype:

model_v2 <- lmer(
  stress ~ age + gender + experien + (expcon|wardid) + (wardtype|wardid), 
  data = nurses
)
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 3 negative eigenvalues
summary(model_v2)
Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ age + gender + experien + (expcon | wardid) + (wardtype |  
    wardid)
   Data: nurses

REML criterion at convergence: 1660.4

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.71832 -0.70404 -0.00175  0.66250  2.83227 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 wardid   (Intercept) 0.17893  0.4230        
          expcon1     0.68068  0.8250   0.33 
 wardid.1 (Intercept) 0.09447  0.3074        
          wardtype1   0.19977  0.4470   -0.94
 Residual             0.21735  0.4662        
Number of obs: 1000, groups:  wardid, 100

Fixed effects:
             Estimate Std. Error t value
(Intercept)  5.655003   0.089447   63.22
age          0.022241   0.002199   10.11
gender1     -0.453405   0.034997  -12.96
experien    -0.061849   0.004475  -13.82

Correlation of Fixed Effects:
         (Intr) age    gendr1
age      -0.358              
gender1  -0.295 -0.015       
experien  0.002 -0.817  0.028
optimizer (nloptwrap) convergence code: 0 (OK)
unable to evaluate scaled gradient
Model failed to converge: degenerate  Hessian with 3 negative eigenvalues

El modelo no convergió. Busquemos el optimizador que logre la convergencia:

model_v2_allfit <- allFit(model_v2, verbose = FALSE)
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 3 negative eigenvalues
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 2 negative eigenvalues
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 3 negative eigenvalues
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 3 negative eigenvalues
glance(model_v2_allfit)
# A tibble: 5 × 9
  optimizer          nobs sigma logLik   AIC   BIC REMLcrit df.residual  NLL_rel
  <chr>             <int> <dbl>  <dbl> <dbl> <dbl>    <dbl>       <int>    <dbl>
1 bobyqa             1000 0.466  -830. 1682. 1736.    1660.         989 0       
2 Nelder_Mead        1000 0.466  -830. 1682. 1736.    1660.         989 1.02e-10
3 nlminbwrap         1000 0.466  -830. 1682. 1736.    1660.         989 3.02e-11
4 nloptwrap.NLOPT_…  1000 0.466  -830. 1682. 1736.    1660.         989 2.67e- 9
5 nloptwrap.NLOPT_…  1000 0.466  -830. 1682. 1736.    1660.         989 1.33e-10

En este caso, fue el optimziador bobyqa. Reajustemos el modelo:

model_v2 <- lmer(
  stress ~ age + gender + experien + (expcon|wardid) + (wardtype|wardid), 
  data = nurses, control = lmerControl(optimizer = "bobyqa")
)
summary(model_v2)
Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ age + gender + experien + (expcon | wardid) + (wardtype |  
    wardid)
   Data: nurses
Control: lmerControl(optimizer = "bobyqa")

REML criterion at convergence: 1660.4

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.71832 -0.70404 -0.00175  0.66250  2.83227 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 wardid   (Intercept) 0.19693  0.4438        
          expcon1     0.78029  0.8833   0.16 
 wardid.1 (Intercept) 0.07646  0.2765        
          wardtype1   0.12532  0.3540   -0.94
 Residual             0.21735  0.4662        
Number of obs: 1000, groups:  wardid, 100

Fixed effects:
             Estimate Std. Error t value
(Intercept)  5.655003   0.089447   63.22
age          0.022241   0.002199   10.11
gender1     -0.453405   0.034997  -12.96
experien    -0.061849   0.004475  -13.82

Correlation of Fixed Effects:
         (Intr) age    gendr1
age      -0.358              
gender1  -0.295 -0.015       
experien  0.002 -0.817  0.028

Evaluemos la significancia de los efectos aleatorios:

set.seed(2024)
tidy(model_v2, conf.int = TRUE, conf.method = "boot", boot.type = "perc")
Computing bootstrap confidence intervals ...

14 message(s): boundary (singular) fit: see help('isSingular')
554 warning(s): Hessian is numerically singular: parameters are not uniquely determined (and others)
Computing bootstrap confidence intervals ...

14 message(s): boundary (singular) fit: see help('isSingular')
574 warning(s): Hessian is numerically singular: parameters are not uniquely determined (and others)
# A tibble: 11 × 8
   effect   group    term        estimate std.error statistic conf.low conf.high
   <chr>    <chr>    <chr>          <dbl>     <dbl>     <dbl>    <dbl>     <dbl>
 1 fixed    <NA>     (Intercept)   5.66     0.0894       63.2  5.48       5.82  
 2 fixed    <NA>     age           0.0222   0.00220      10.1  0.0182     0.0269
 3 fixed    <NA>     gender1      -0.453    0.0350      -13.0 -0.520     -0.387 
 4 fixed    <NA>     experien     -0.0618   0.00448     -13.8 -0.0707    -0.0532
 5 ran_pars wardid   sd__(Inter…   0.444   NA            NA    0.279      0.516 
 6 ran_pars wardid   cor__(Inte…   0.163   NA            NA   -0.00265    0.372 
 7 ran_pars wardid   sd__expcon1   0.883   NA            NA    0.675      1.13  
 8 ran_pars wardid.1 sd__(Inter…   0.277   NA            NA    0.00183    0.552 
 9 ran_pars wardid.1 cor__(Inte…  -0.936   NA            NA   -1.00      -0.401 
10 ran_pars wardid.1 sd__wardty…   0.354   NA            NA    0.202      0.515 
11 ran_pars Residual sd__Observ…   0.466   NA            NA    0.444      0.485

Vemos que han habido algunos problemas de convergencia a la hora de calcular los intervalos de confianza mediante Bootstrap, por lo que no podemos estar totalmente seguros que estos resultados sean confiables. Si obviamos estos problemas, solo para efectos prácticamos, podemos observar que los efectos aleatorios no correlacionados de expcon y wardtype son significativos.

Ejercicio 2

Podemos ajustar el modelo de tres niveles con interceptos aleatorios para los pabellones dentro de cada hospital y para los hospitales usando las siguiente líneas de código:

model_ri_3lvl <- lmer(stress ~ (1|hospital/ward), data = nurses)
summary(model_ri_3lvl)
Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ (1 | hospital/ward)
   Data: nurses

REML criterion at convergence: 1945

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.97604 -0.65739  0.01792  0.67398  3.11229 

Random effects:
 Groups        Name        Variance Std.Dev.
 ward:hospital (Intercept) 0.4888   0.6992  
 hospital      (Intercept) 0.1743   0.4175  
 Residual                  0.3013   0.5489  
Number of obs: 1000, groups:  ward:hospital, 100; hospital, 25

Fixed effects:
            Estimate Std. Error t value
(Intercept)   5.0010     0.1103   45.34

Nótese que se usa el identificador ward y no wardid con en los ejercicios anteriores. La razón es que los valores de wardid no están anidados dentro de los valores de hospital, ya que esta variable identifica a cada pabellón idenpendientemente del hospital al que pertenece.

Por otro lado, en la salida del modelo vemos que el efecto aleatorio (1|hospital/ward) se expande en los efectos aleatorios del hospital ((1|hospital)) y del pabellón relativo a cada hospital ((1|hospital:ward)). Por esta razón, también podemos ajustar este modelo la siguiente manera:

model_ri_3lvl <- lmer(stress ~ (1|hospital) + (1|hospital:ward), data = nurses)
summary(model_ri_3lvl)
Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ (1 | hospital) + (1 | hospital:ward)
   Data: nurses

REML criterion at convergence: 1945

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.97604 -0.65739  0.01792  0.67398  3.11229 

Random effects:
 Groups        Name        Variance Std.Dev.
 hospital:ward (Intercept) 0.4888   0.6992  
 hospital      (Intercept) 0.1743   0.4175  
 Residual                  0.3013   0.5489  
Number of obs: 1000, groups:  hospital:ward, 100; hospital, 25

Fixed effects:
            Estimate Std. Error t value
(Intercept)   5.0010     0.1103   45.34

Ahora, ajustemos el modelo de dos niveles con interceptos aleatorios para los pabellones (indistintamente de a qué hospital pertenecen) para hacer la comparación:

model_ri_2lvl <- lmer(stress ~ (1|wardid), data = nurses)
summary(model_ri_2lvl)
Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ (1 | wardid)
   Data: nurses

REML criterion at convergence: 1952.4

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.94699 -0.67691 -0.00005  0.69678  3.12110 

Random effects:
 Groups   Name        Variance Std.Dev.
 wardid   (Intercept) 0.6576   0.8109  
 Residual             0.3013   0.5489  
Number of obs: 1000, groups:  wardid, 100

Fixed effects:
            Estimate Std. Error t value
(Intercept)  5.00065    0.08295   60.28

Para calcular el coeficiente de correlación interclase (ICC) usamos la función icc() del paquete performance. Primero, para el modelo de dos niveles:

library(performance)
icc(model_ri_2lvl)
# Intraclass Correlation Coefficient

    Adjusted ICC: 0.686
  Unadjusted ICC: 0.686

Ahora, para el modelo de tres niveles:

icc(model_ri_3lvl)
# Intraclass Correlation Coefficient

    Adjusted ICC: 0.688
  Unadjusted ICC: 0.688

Vemos que la proporción de varianza explicada por los factores de agrupación (niveles) en el modelo de tres niveles es mayor que la de los factores de agrupación en el modelo de dos niveles. Podemos también separa el ICC por los factores de agrupación de a partir del segundo nivel:

icc(model_ri_3lvl, by_group = TRUE)
# ICC by Group

Group         |   ICC
---------------------
hospital:ward | 0.507
hospital      | 0.181

Vemos que la proporción de varianza explicada por pabellones dentro de cada hospital es mayor que la explicada por los hospitales.

Por último, para comparar la calidad de ajuste de los modelos, podemos usar la función anova():

anova(model_ri_2lvl, model_ri_3lvl)
refitting model(s) with ML (instead of REML)
Data: nurses
Models:
model_ri_2lvl: stress ~ (1 | wardid)
model_ri_3lvl: stress ~ (1 | hospital) + (1 | hospital:ward)
              npar    AIC  BIC  logLik deviance  Chisq Df Pr(>Chisq)   
model_ri_2lvl    3 1955.3 1970 -974.64   1949.3                        
model_ri_3lvl    4 1950.4 1970 -971.18   1942.4 6.9195  1   0.008526 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Podemos observar que el AIC del modelo de tres niveles es menor que el del modelo de dos niveles. Por tanto, el primero brinda un mejor ajuste. Además, dado que los modelos son anidados, podemos evaluar la significancia del modelo de tres niveles con respecto al de dos niveles. En este caso, vemos que el p-valor de la prueba ji al cuadrado es significativo y, por tanto, el modelo de tres niveles es significativo sobre el de dos niveles.

Ejercicio 3

Para que al función lmer() devuelva las pruebas de significancia para los efectos fijos necesitamos llamar antes al paquete lmerTest:


Attaching package: 'lmerTest'
The following object is masked from 'package:lme4':

    lmer
The following object is masked from 'package:pracma':

    rand
The following object is masked from 'package:stats':

    step

Ahora, ajustamos el modelo con las espeficicaciones indicadas en el ejercicio:

model_full_3lvl <- lmer(
  stress ~ age + gender + experien + expcon + wardtype + hospsize + (expcon|hospital) + 
    (wardtype|hospital) + (hospsize|hospital:ward), data = nurses
)
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 1 negative eigenvalues
Warning: Model failed to converge with 1 negative eigenvalue: -3.0e-05
summary(model_full_3lvl)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: stress ~ age + gender + experien + expcon + wardtype + hospsize +  
    (expcon | hospital) + (wardtype | hospital) + (hospsize |  
    hospital:ward)
   Data: nurses

REML criterion at convergence: 1608.4

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.66405 -0.69679 -0.00233  0.63510  2.76914 

Random effects:
 Groups        Name        Variance Std.Dev. Corr 
 hospital.ward (Intercept) 0.10032  0.3167        
               hospsize    0.06596  0.2568   -0.56
 hospital      (Intercept) 0.08239  0.2870        
               wardtype1   0.03144  0.1773   -0.10
 hospital.1    (Intercept) 0.11122  0.3335        
               expcon1     0.64523  0.8033   -0.62
 Residual                  0.21733  0.4662        
Number of obs: 1000, groups:  hospital:ward, 100; hospital, 25

Fixed effects:
              Estimate Std. Error         df t value Pr(>|t|)    
(Intercept)   5.523071   0.158393  29.170334  34.869  < 2e-16 ***
age           0.022235   0.002196 909.104890  10.123  < 2e-16 ***
gender1      -0.453315   0.034894 914.051118 -12.991  < 2e-16 ***
experien     -0.061739   0.004464 915.765552 -13.831  < 2e-16 ***
expcon1      -0.711134   0.175172  20.524193  -4.060 0.000586 ***
wardtype1     0.081922   0.077054  13.139514   1.063 0.306852    
hospsize      0.277322   0.129052  22.163320   2.149 0.042818 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
          (Intr) age    gendr1 expern expcn1 wrdty1
age       -0.197                                   
gender1   -0.168 -0.013                            
experien  -0.004 -0.817  0.028                     
expcon1   -0.324  0.003 -0.002  0.000              
wardtype1 -0.206 -0.012 -0.001  0.014  0.000       
hospsize  -0.633 -0.005  0.003  0.004 -0.008 -0.004
optimizer (nloptwrap) convergence code: 0 (OK)
unable to evaluate scaled gradient
Model failed to converge: degenerate  Hessian with 1 negative eigenvalues

Vemos que el modelo no ha convergido. Evaluemos otros optimizadores:

model_full_3lvl_allfit <- allFit(model_full_3lvl, verbose = FALSE)
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
unable to evaluate scaled gradient
Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge: degenerate Hessian with 1 negative eigenvalues
Warning: Model failed to converge with 1 negative eigenvalue: -3.0e-05
glance(model_full_3lvl_allfit)
# A tibble: 5 × 9
  optimizer          nobs sigma logLik   AIC   BIC REMLcrit df.residual  NLL_rel
  <chr>             <int> <dbl>  <dbl> <dbl> <dbl>    <dbl>       <int>    <dbl>
1 bobyqa             1000 0.466  -804. 1642. 1726.    1608.         983 0       
2 Nelder_Mead        1000 0.466  -804. 1642. 1726.    1608.         983 4.88e-11
3 nlminbwrap         1000 0.466  -804. 1642. 1726.    1608.         983 7.64e- 9
4 nloptwrap.NLOPT_…  1000 0.466  -804. 1642. 1726.    1608.         983 1.04e- 8
5 nloptwrap.NLOPT_…  1000 0.466  -804. 1642. 1726.    1608.         983 2.78e- 8

El optimizador con el que se logra la convergencia es bobyqa. Reajustemos el modelo:

model_full_3lvl <- lmer(
  stress ~ age + gender + experien + expcon + wardtype + hospsize + (expcon|hospital) + 
    (wardtype|hospital) + (hospsize|hospital:ward), 
  data = nurses, control = lmerControl(optimizer = "bobyqa")
)
summary(model_full_3lvl)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: stress ~ age + gender + experien + expcon + wardtype + hospsize +  
    (expcon | hospital) + (wardtype | hospital) + (hospsize |  
    hospital:ward)
   Data: nurses
Control: lmerControl(optimizer = "bobyqa")

REML criterion at convergence: 1608.4

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.66405 -0.69679 -0.00233  0.63510  2.76914 

Random effects:
 Groups        Name        Variance Std.Dev. Corr 
 hospital.ward (Intercept) 0.10033  0.3167        
               hospsize    0.06597  0.2569   -0.56
 hospital      (Intercept) 0.01405  0.1185        
               wardtype1   0.03145  0.1773   -0.25
 hospital.1    (Intercept) 0.17955  0.4237        
               expcon1     0.64520  0.8032   -0.49
 Residual                  0.21733  0.4662        
Number of obs: 1000, groups:  hospital:ward, 100; hospital, 25

Fixed effects:
              Estimate Std. Error         df t value Pr(>|t|)    
(Intercept)   5.523076   0.158393  29.159813  34.870  < 2e-16 ***
age           0.022235   0.002196 909.104788  10.123  < 2e-16 ***
gender1      -0.453315   0.034894 914.051154 -12.991  < 2e-16 ***
experien     -0.061739   0.004464 915.765535 -13.831  < 2e-16 ***
expcon1      -0.711134   0.175168  20.523124  -4.060 0.000586 ***
wardtype1     0.081922   0.077056  13.121689   1.063 0.306892    
hospsize      0.277315   0.129053  22.157302   2.149 0.042827 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
          (Intr) age    gendr1 expern expcn1 wrdty1
age       -0.197                                   
gender1   -0.168 -0.013                            
experien  -0.004 -0.817  0.028                     
expcon1   -0.324  0.003 -0.002  0.000              
wardtype1 -0.206 -0.012 -0.001  0.014  0.000       
hospsize  -0.633 -0.005  0.003  0.004 -0.008 -0.004

De los resultados del modelo, vemos que todos los efectos fijos son significativos con excepción del efecto fijo del tipo de pabellón (wardtype).

Ahora, comparemos este modelo y el modelo de tres niveles con solo interceptos aleatorios:

anova(model_ri_3lvl, model_full_3lvl)
refitting model(s) with ML (instead of REML)
Data: nurses
Models:
model_ri_3lvl: stress ~ (1 | hospital) + (1 | hospital:ward)
model_full_3lvl: stress ~ age + gender + experien + expcon + wardtype + hospsize + (expcon | hospital) + (wardtype | hospital) + (hospsize | hospital:ward)
                npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)    
model_ri_3lvl      4 1950.4 1970.0 -971.18   1942.4                         
model_full_3lvl   17 1606.7 1690.1 -786.35   1572.7 369.67 13  < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Vemos que, según el AIC, este modelo con efectos mixtos tiene un mucho mejor ajuste que el modelo anterior con solo interceptos aleatorios. Además, la prueba de significancia resultó significativa, por lo que tenemos evidencia estadística para afirmar que el modelo de tres niveles con efectos mixtos brinda un mejor ajuste que el modelo de tres niveles con interceptos aleatorios.