12 Regresión lineal: Conceptos básicos
En este capítulo, veremos algunas herramientas para hacer un análisis de regresión lineal en R. El análisis de regresión lineal consiste en la construcción de un modelo de regresión lineal, el cual es un modelo matemático que nos permite aproximar la asociación entre una variable de respuesta escalar y una o más variables explicativas o predictoras usando una función lineal.
En general, un modelo de regresión lineal puede usarse para inferencia o predicción. Estos objetivos responden a preguntas distintas. Digamos que queremos construir un modelo de regresión lineal para explicar el ingreso bruto (en soles, por ejemplo) y los años de estudio de un grupo de personas. Podemos usar un modelo de regresión lineal para responder las siguientes preguntas según nuestro objetivo:
- Inferencia: ¿Existe una asociación estadísticamente significative entre el ingreso bruto y los años de estudio de este grupo de personas? ¿Es esta asociación lineal?
- Predicción: Si solo tengo el dato del ingreso bruto de una persona, ¿cuál es el ingreso bruto de una persona? ¿Qué tan precisa es esta predicción?
En este libro le daremos más énfasis a la inferencia, es decir, a encontrar modelos que nos ayuden a determinar qué variables predictoras están asociadas con la variable de respuesta y si esta asociación es lineal. Sin embargo, cuando sea necesario, haremos comentarios sobre cómo evaluar el poder predictivo de un modelo de regresión lineal, particularmente para comparar múltiples modelos.
12.1 Volumen espiratorio forzado en niños
En este capítulo usaremos el conjunto de datos del archivo fev.csv. Este archivo contiene parte de las observaciones del estudio realizado por Tager et al. (1979), quienes investigaron el efecto del tabaquismo de los padres en la función pulmonar de 654 niños y adolescentes de 3 a 19 años de edad en East Boston, Massachusetts. Este archivo fue recuperado del repositorio de recursos de Rosner (2015).
Llamemos al paquete tidyverse y usemos la función read_csv() para leer la base:
Podemos usar el comando View(fev) para dar un vistazo a la data:
View(fev)En este conjunto de datos, la columna id es el identificador de cada niño, age es la edad en años, fev es el volumen espiratorio forzado entre 25% y 75% de la capacidad vital en litro, hgt es la altura en pulgadas, sex es el sexo (0: Mujer, 1: Hombre) y smoke es la condición de fumador (0: No fuma, 1: Sí fuma).
12.2 Regresión lineal simple
El caso más simple de un modelo de regresión lineal es cuando usamos solo una variable predictora para explicar la variable de respuesta. En este caso, al modelo de regresión lineal se le llama modelo de regresión lineal simple. Como ejemplo, construiremos un modelo de regresión lineal con el volumen espiratorio forzado (fev) de los niños como variable de respuesta y la altura (hgt) como su única variable predictora.
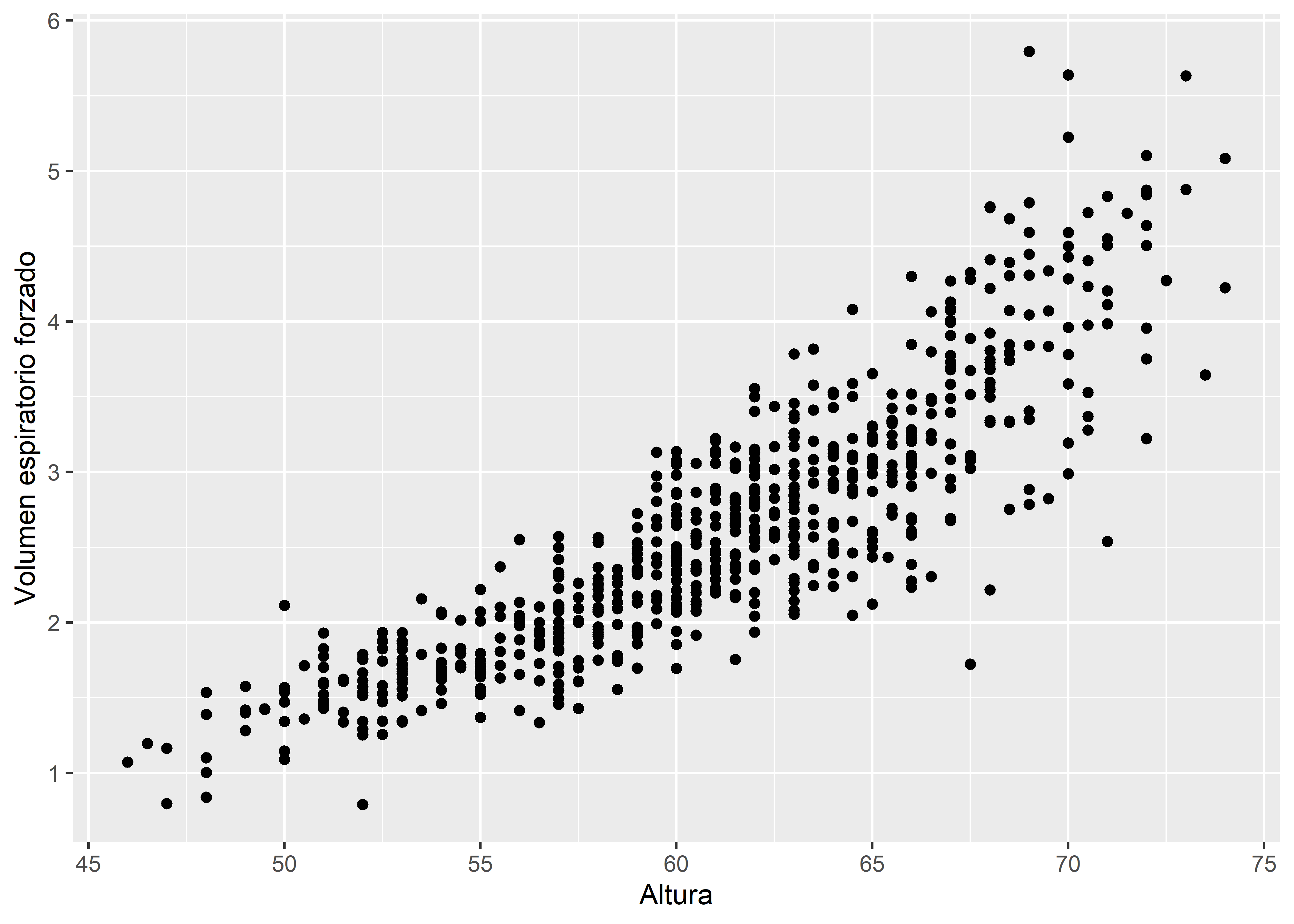
Primero veamos un gráfico de dispersión entre hgt y fev para analizar visualmente la asociación entre estas variables:
fev %>%
ggplot(aes(hgt, fev)) +
geom_point() +
labs(x = "Altura", y = "Volumen espiratorio forzado")En la Figura 12.1, vemos que la asociación entre las variables es aproximadamente lineal. Por lo tanto, un modelo de regresión lineal es conveniente para representar esta asociación.
12.2.1 Ajuste del modelo
En R podemos ajustar un modelo de regresión lineal a un conjunto de datos usando la función lm(). Esta función se utiliza de la siguiente manera:
lm(formula, data, ...)El parámetro fórmula es una expresión de la forma y ~ x, donde y y x hacen referencia al nombre de la variable de respuesta y al de la variable predictora en en el objeto data, respectivamente. En nuestro caso, la fórmula estaría dada por fev ~ hgt y la data por fev. Ejecutamos la función y almacenamos los resultados en un objeto:
fit_simple <- lm(fev ~ hgt, fev)Para ver un resumen de resultados del ajuste del modelo usamos la función summary():
summary(fit_simple)
Call:
lm(formula = fev ~ hgt, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.75167 -0.26619 -0.00401 0.24474 2.11936
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.432679 0.181460 -29.94 <2e-16 ***
hgt 0.131976 0.002955 44.66 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4307 on 652 degrees of freedom
Multiple R-squared: 0.7537, Adjusted R-squared: 0.7533
F-statistic: 1995 on 1 and 652 DF, p-value: < 2.2e-16Este resumen contiene las siguientes secciones:
-
Call: La función ejecutada. -
Residuals: Estadísticas descriptivas de los residuales. -
Coefficients: Tabla con los coeficientes estimados (Estimate), sus errores estándar (Std. Error), valor de la estadísticat value) y el p-valor de la prueba de significancia (Pr(>|t|)). Adicionalmente, se incluyen códigos para los niveles de significancia (Por ejemplo,***quiere decir que la prueba resultó significativa a un nivel de significancia de 0.001, ya que el p-valor está entre 0 y 0.001). -
Residual standard error: Error estándar residual (raíz cuadrada del promedio de los residuales al cuadrado) y grados de libertad. -
Multiple R-squared: -
Adjusted R-squared: -
F-statistic: Estadística -
p-value: p-valor de la prueba de significancia del modelo.
Para poder manejar mejor los resultados, podemos pasarlos a una tabla o data frame. La función tidy() del paquete broom nos permite hacer esto:
# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -5.43 0.181 -29.9 1.45e-124
2 hgt 0.132 0.00295 44.7 1.57e-200Por defecto, la función tidy() muestra los términos del modelo (term), las estimaciones (estimates), los errores estándar (std.error), la estadística de prueba (statistic) y el p-valor de la prueba de significancia (p.value).
De estos resultados, podemos ver que la estimación del intercepto es de -5.4327 con error estándar (SE, por sus siglas en inglés) de 0.1815, mientras que la estimación del coeficiente de hgt es de 0.1320 (SE = 0.003). Con estos valores, podemos escribir el modelo de regresión lineal ajustado o ecuación de predicción:
De la estimación del coeficiente de hgt podemos decir que se estima que el aumento en la altura de 1 pulgada está asociado con un aumento en el volumen espiratorio forzado de 0.1320 L, en promedio.
La ecuación de predicción Ecuación 12.1 representa una línea recta. Para visualizarla podemos usar la función geom_smooth() del paquete ggplot2 incluyendo los argumentos method = lm y formula = y ~ x:
fev %>%
ggplot(aes(hgt, fev)) +
geom_point() +
geom_smooth(method = lm, formula = y ~ x) +
labs(x = "Altura", y = "Volumen espiratorio forzado") 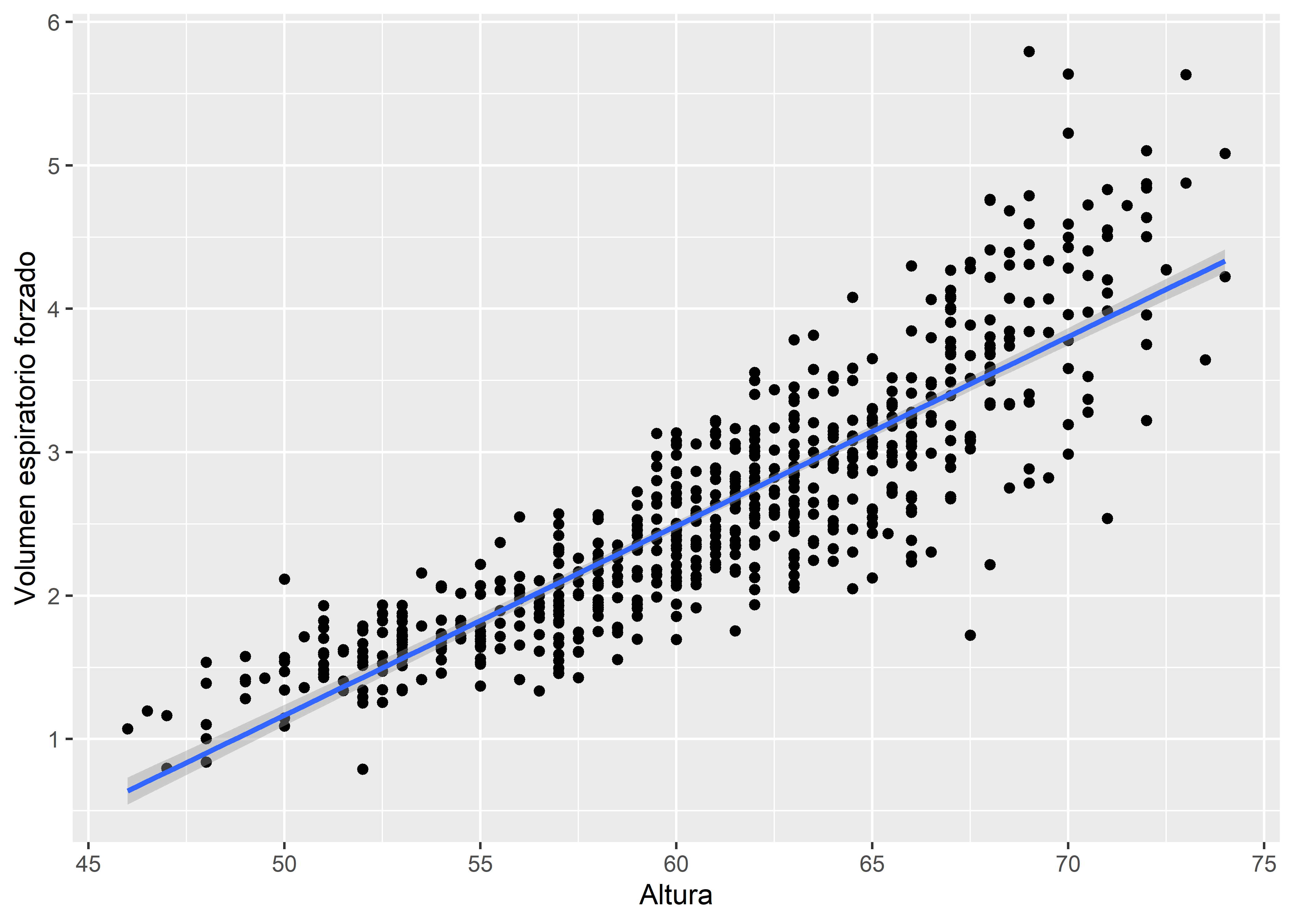
La línea recta azul es la gráfica de la ecuación Ecuación 12.1. Adicionalmente, se muestra una banda de confianza de color gris alrededor de la línea, la cual se construye a partir de los intervalos de confianza de los valores esperados de la variable de respuesta. Por defecto, la banda tiene un nivel de confianza de 95%.
12.2.2 Intervalos de confianza de los coeficientes
Los intervalos de confianza de los coeficientes estimados pueden calcularse usando la función confint():
confint(fit_simple) 2.5 % 97.5 %
(Intercept) -5.7889951 -5.076363
hgt 0.1261732 0.137778Por defecto, esta función calcula los intervalos al 95% de confianza. Para cambiar el nivel de confianza, podemos usar el parámetro level. Por ejemplo, a un 90% de confianza:
confint(fit_simple, level = 0.9) 5 % 95 %
(Intercept) -5.7315784 -5.133779
hgt 0.1271082 0.136843También podemos usar la función tidy() para construir los intervalos de confianza y mostrar los límites inferiores y superiores en una tabla. Para esto agregamos el argumento conf.int = TRUE en la función:
tidy(fit_simple, conf.int = TRUE)# A tibble: 2 × 7
term estimate std.error statistic p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -5.43 0.181 -29.9 1.45e-124 -5.79 -5.08
2 hgt 0.132 0.00295 44.7 1.57e-200 0.126 0.138Al final de la tabla, la función añade una columna con el límite de confianza inferior (conf.low) y otra con el limíte de confianza superior (conf.high). Por defecto, se calcula límites al 95% de confianza. Para cambiar el nivel, usamos el argumento conf.level. Por ejemplo, al 90% de confianza:
tidy(fit_simple, conf.int = TRUE, conf.level = 0.9)# A tibble: 2 × 7
term estimate std.error statistic p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -5.43 0.181 -29.9 1.45e-124 -5.73 -5.13
2 hgt 0.132 0.00295 44.7 1.57e-200 0.127 0.13712.2.3 Predicción de la respuesta
Podemos usar el modelo de regresión ajustado para hacer predicciones de la respuesta dado un conjunto de valores del predictores. A estas predicciones se les conoce como valores predichos. Para calcular estas predicciones se usa la ecuación de predicción. Por ejemplo, si queremos predecir cuánto será el volumen espiratorio forzado de un niño o niña de 55.2 pulgadas de altura usando la ecuación Ecuación 12.1, reemplazamos hgt por 55.2 y tenemos que la predicción de fev es -5.4327 + 0.1320(55.2) = 1.8537.
Para obtener los valores predichos de la respuesta dados los valores del predictor en la data que se usó para ajustar el modelo, podemos usar la función fitted(). Por ejemplo, los 5 primeros valores predichos de fev usando el modelo fit_simple son:
fitted(fit_simple)[1:5] 1 2 3 4 5
2.089929 3.475672 1.759990 1.562026 2.089929 A estos valores predichos también se le conocen como valores ajustados. Estos valores predichos corresponden a reemplazar en la ecuación Ecuación 12.1 los 5 primeros valores de la variable predictora hgt:
coefficients(fit_simple)[1] + coefficients(fit_simple)[2] * fev$hgt[1:5][1] 2.089929 3.475672 1.759990 1.562026 2.089929Es posible también obtener los valores ajustados llamando al objeto fitted.values que contiene el objeto fit_simple donde está el modelo:
fit_simple$fitted.values[1:10] 1 2 3 4 5 6 7 8
2.089929 3.475672 1.759990 1.562026 2.089929 2.617831 2.221904 1.957953
9 10
2.287892 2.485855 La función fitted() solo devuelve los valores predichos calculados a partir de la data que se usó para ajustar el modelo. Una función más general es la función predict(), la cual permite también pasar un conjunto de valores nuevos de la variable predictora. Por defecto, si no pasamos un conjunto de valores nuevos, predict() devuelve los valores ajustados:
predict(fit_simple)[1:5] 1 2 3 4 5
2.089929 3.475672 1.759990 1.562026 2.089929 Creemos ahora un conjunto de valores nuevos de la variable predictora. Usaremos la función runif() para generar un vector de 5 números aleatorios entre el mínimo y el máximo de hgt:
set.seed(2023)
new_data <- tibble(hgt = runif(n = 5, min = min(fev$hgt), max = max(fev$hgt)))
new_data# A tibble: 5 × 1
hgt
<dbl>
1 59.1
2 55.4
3 50.6
4 57.1
5 46.9Los datos deben almacenarse en un data frame y la columna que contiene los nuevos datos debe llamarse igual que la variable predictora.
Luego, pasamos estos nuevos valores al parámetro newdata de la función predict():
predict(fit_simple, newdata = new_data) 1 2 3 4 5
2.3624834 1.8768340 1.2398598 2.1019861 0.7505045 De esta manera, obtenemos las predicciones de fev dados nuevos valores del predictor hgt.
Para obtener los valores predichos en una tabla, podemos usar la función augment() del paquete broom:
augment(fit_simple)# A tibble: 5 × 8
fev hgt .fitted .resid .hat .sigma .cooksd .std.resid
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1.71 57 2.09 -0.382 0.00234 0.431 0.000923 -0.888
2 1.72 67.5 3.48 -1.75 0.00343 0.425 0.0286 -4.07
3 1.72 54.5 1.76 -0.0400 0.00361 0.431 0.0000157 -0.0930
4 1.56 53 1.56 -0.00403 0.00465 0.431 0.000000205 -0.00937
5 1.90 57 2.09 -0.195 0.00234 0.431 0.000241 -0.453 Aquí solo se muestran las primeras 5 filas, pero la tabla resultante debería tener el mismo número de filas que la tabla fev (654). La función augment() devuelve las variables del modelo, fev y hgt y las predicciones en la columna .fitted. Además, devuelve los residuales (.resid) y otras estadísticas de ajuste basados en estos.
Si queremos calcular los errores estándar de los valores predichos agregamos el argumento se_fit = TRUE:
augment(fit_simple, se_fit = TRUE)# A tibble: 5 × 9
fev hgt .fitted .se.fit .resid .hat .sigma .cooksd .std.resid
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1.71 57 2.09 0.0208 -0.382 0.00234 0.431 0.000923 -0.888
2 1.72 67.5 3.48 0.0252 -1.75 0.00343 0.425 0.0286 -4.07
3 1.72 54.5 1.76 0.0259 -0.0400 0.00361 0.431 0.0000157 -0.0930
4 1.56 53 1.56 0.0294 -0.00403 0.00465 0.431 0.000000205 -0.00937
5 1.90 57 2.09 0.0208 -0.195 0.00234 0.431 0.000241 -0.453 En el caso de que queramos usar un nuevo conjunto de valores del predictor en la función augment(), lo pasamos al parámetro newdata:
augment(fit_simple, newdata = new_data, se_fit = TRUE)# A tibble: 5 × 3
hgt .fitted .se.fit
<dbl> <dbl> <dbl>
1 59.1 2.36 0.0179
2 55.4 1.88 0.0239
3 50.6 1.24 0.0355
4 57.1 2.10 0.0207
5 46.9 0.751 0.045512.2.3.1 Incertidumbre de valores predichos
La incertidumbre de los valores predichos depende del tipo de predicción que se quiera realizar:
Si el objetivo es predecir el valor esperado o medio de la respuesta dado un valor particular de la variable predictora, entonces la incertidumbre de la predicción se expresa mediante un intervalo de confianza.
Si el objetivo es predecir un caso individual o una nueva observación de la respuesta dado un valor particular de la variable predictora, entonces la incertidumbre de la predicción se expresa mediante un intervalo de predicción, también conocido como intervalo de tolerancia.
Técnicamente, la predicción del valor medio o de un caso individual es la misma dado un valor particular del predictor. Sin embargo, lo que los diferencia son sus intervalos de incertidumbre. Los intervalos de predicción son más amplios que los intervalos de confianza, ya que existe mayor incertidumbre para predecir un caso individual que para predecir la media de una distribución de valores.
Para hallar los intervalos de confianza de las predicciones de los valores esperados, podemos agregar el argumento interval = "confidence" en la función predict(). Por ejemplo, usando los primeros 5 valores del predictor en la data obtenemos las siguientes predicciones del valor medio de la respuesta y sus intervalos de confianza:
predict(fit_simple, interval = "confidence")[1:5,] fit lwr upr
1 2.089929 2.049044 2.130814
2 3.475672 3.426136 3.525209
3 1.759990 1.709201 1.810779
4 1.562026 1.504352 1.619701
5 2.089929 2.049044 2.130814Por defecto, la función devuelve los intervalos al 95% de confianza. El límite inferior se encuentra en la columna lwr, mientras que el límite superior en upr. Si queremos cambiar el nivel de confianza, podemos usar el parámetro level. Por ejemplo, para un 90% de confianza:
predict(fit_simple, interval = "confidence", level = 0.9)[1:5,] fit lwr upr
1 2.089929 2.055632 2.124226
2 3.475672 3.434118 3.517226
3 1.759990 1.717385 1.802595
4 1.562026 1.513646 1.610407
5 2.089929 2.055632 2.124226Por el contrario, si quisieramos calcular los intervalos de predicción, agregamos el argumento interval = "prediction". Por ejemplo, usando los valores del predictor en new_data:
predict(fit_simple, newdata = new_data, interval = "prediction") fit lwr upr
1 2.3624834 1.51607248 3.208894
2 1.8768340 1.02984967 2.723818
3 1.2398598 0.39130926 2.088410
4 2.1019861 1.25533452 2.948638
5 0.7505045 -0.09987401 1.600883Podemos también usar la función augment() del paquete broom para calcular los intervalos de confianza o de predicción usando los mismos argumentos que agregamos en la función predict(). Por ejemplo, para los intervalos de confianza:
augment(fit_simple, interval = "confidence")# A tibble: 5 × 10
fev hgt .fitted .lower .upper .resid .hat .sigma .cooksd .std.resid
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1.71 57 2.09 2.05 2.13 -0.382 0.00234 0.431 9.23e-4 -0.888
2 1.72 67.5 3.48 3.43 3.53 -1.75 0.00343 0.425 2.86e-2 -4.07
3 1.72 54.5 1.76 1.71 1.81 -0.0400 0.00361 0.431 1.57e-5 -0.0930
4 1.56 53 1.56 1.50 1.62 -0.00403 0.00465 0.431 2.05e-7 -0.00937
5 1.90 57 2.09 2.05 2.13 -0.195 0.00234 0.431 2.41e-4 -0.453 El límite de inferior del intervalo de confianza se encuentra en la columna .lower y el superior en .upper. Un detalle importante es que esta función no permite cambiar el nivel de confianza, el cual es por defecto de 95%. En el caso de los intervalos de predicción:
augment(fit_simple, se_fit = TRUE, interval = "prediction")# A tibble: 5 × 4
hgt .fitted .lower .upper
<dbl> <dbl> <dbl> <dbl>
1 59.1 2.36 1.52 3.21
2 55.4 1.88 1.03 2.72
3 50.6 1.24 0.391 2.09
4 57.1 2.10 1.26 2.95
5 46.9 0.751 -0.0999 1.60Otra opción para calcular los intervalos de incertidumbre de las predicciones son las funciones estimate_expectation() y estimate_prediction() del paquete modelbased. estimate_expectation() produce intervalos de confianza y estimate_prediction() intervalos de predicción. En estos casos, no es necesario especificar el tipo de intervalo de incertidumbe.
Por ejemplo, con estimate_expectation:
library(modelbased)
estimate_expectation(fit_simple)Model-based Expectation
hgt | Predicted | SE | 95% CI | Residuals
---------------------------------------------------
57.00 | 2.09 | 0.02 | [2.05, 2.13] | -0.38
67.50 | 3.48 | 0.03 | [3.43, 3.53] | -1.75
54.50 | 1.76 | 0.03 | [1.71, 1.81] | -0.04
53.00 | 1.56 | 0.03 | [1.50, 1.62] | -4.03e-03
57.00 | 2.09 | 0.02 | [2.05, 2.13] | -0.19
Variable predicted: fevAquí se muestran solo las 5 primeras filas. Esta función devuelve un data frame pero lo imprime de una manera más estética. Para ver el data frame de manera normal podemos usar la función tibble() del paquete tibble (el paquete tibble se carga junto con tidyverse):
fit_simple %>%
estimate_expectation() %>%
as_tibble()# A tibble: 5 × 6
hgt Predicted SE CI_low CI_high Residuals
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 57 2.09 0.0208 2.05 2.13 -0.382
2 67.5 3.48 0.0252 3.43 3.53 -1.75
3 54.5 1.76 0.0259 1.71 1.81 -0.0400
4 53 1.56 0.0294 1.50 1.62 -0.00403
5 57 2.09 0.0208 2.05 2.13 -0.195 Esta función devuelve los valores de la variable de predictora (hgt), los valores predichos (Predicted), los errores estándar de los valores predichos (SE), los límites inferiores (CI_low) y superiores (CI_high) al 95% de confianza de los valores esperados, y los residuales (Residuals). Para cambiar el nivel de confianza se usa el parámetro ci. Por ejemplo, al 90% de confianza:
fit_simple %>%
estimate_expectation(ci = 0.9) %>%
as_tibble()# A tibble: 5 × 6
hgt Predicted SE CI_low CI_high Residuals
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 57 2.09 0.0208 2.06 2.12 -0.382
2 67.5 3.48 0.0252 3.43 3.52 -1.75
3 54.5 1.76 0.0259 1.72 1.80 -0.0400
4 53 1.56 0.0294 1.51 1.61 -0.00403
5 57 2.09 0.0208 2.06 2.12 -0.195 Para hallar los intervalos de predicción, usamos la función estimate_expectation. Los valores del predictor para los cuales queremos hacer las predicciones se pasan en el parámetro data:
estimate_prediction(fit_simple, data = new_data)Model-based Prediction
hgt | Predicted | SE | 95% CI
----------------------------------------
59.07 | 2.36 | 0.43 | [ 1.52, 3.21]
55.39 | 1.88 | 0.43 | [ 1.03, 2.72]
50.56 | 1.24 | 0.43 | [ 0.39, 2.09]
57.09 | 2.10 | 0.43 | [ 1.26, 2.95]
46.85 | 0.75 | 0.43 | [-0.10, 1.60]
Variable predicted: fevAl 90% de tolerancia:
estimate_prediction(fit_simple, data = new_data, ci = 0.9)Model-based Prediction
hgt | Predicted | SE | 90% CI
---------------------------------------
59.07 | 2.36 | 0.43 | [1.65, 3.07]
55.39 | 1.88 | 0.43 | [1.17, 2.59]
50.56 | 1.24 | 0.43 | [0.53, 1.95]
57.09 | 2.10 | 0.43 | [1.39, 2.81]
46.85 | 0.75 | 0.43 | [0.04, 1.46]
Variable predicted: fev12.3 Regresión lineal múltiple
Un modelo de regresión lineal múltiple es aquel en el que se usa una función lineal de más de una variable predictora para predecir la variable de respuesta. De manera general, si hgt) y edad (age) para predecir el volumen espiratorio forzado (fev).
Previamente a la construcción del modelo, realicemos un análisis exploratorio. En el caso de una regresión lineal simple, vimos mediante un gráfico de dispersión que la asociación entre el volumen espiratorio forzado y la altura era aproximadamente lineal. En el caso de tener varios predictores, se podrían hacer gráficos separados por cada predictor para evaluar la asociación de estos con la respuesta. Sin embargo, de encontrar una asociación aproximadamente lineal por separado, esto no necesariamente significa que el modelo de regresión lineal múltiple sea el adecuado. La mejor opción para evaluar si el modelo es adecuado es primero estimarlo y luego evaluar su ajuste a los datos.
Para evaluar rápidamente la asociación de varias variables podemos usar la función ggpairs() del paquete GGally. Seleccionamos de los datos las variables que queremos examinar y pasamos la selección a la función ggpairs():
Registered S3 method overwritten by 'GGally':
method from
+.gg ggplot2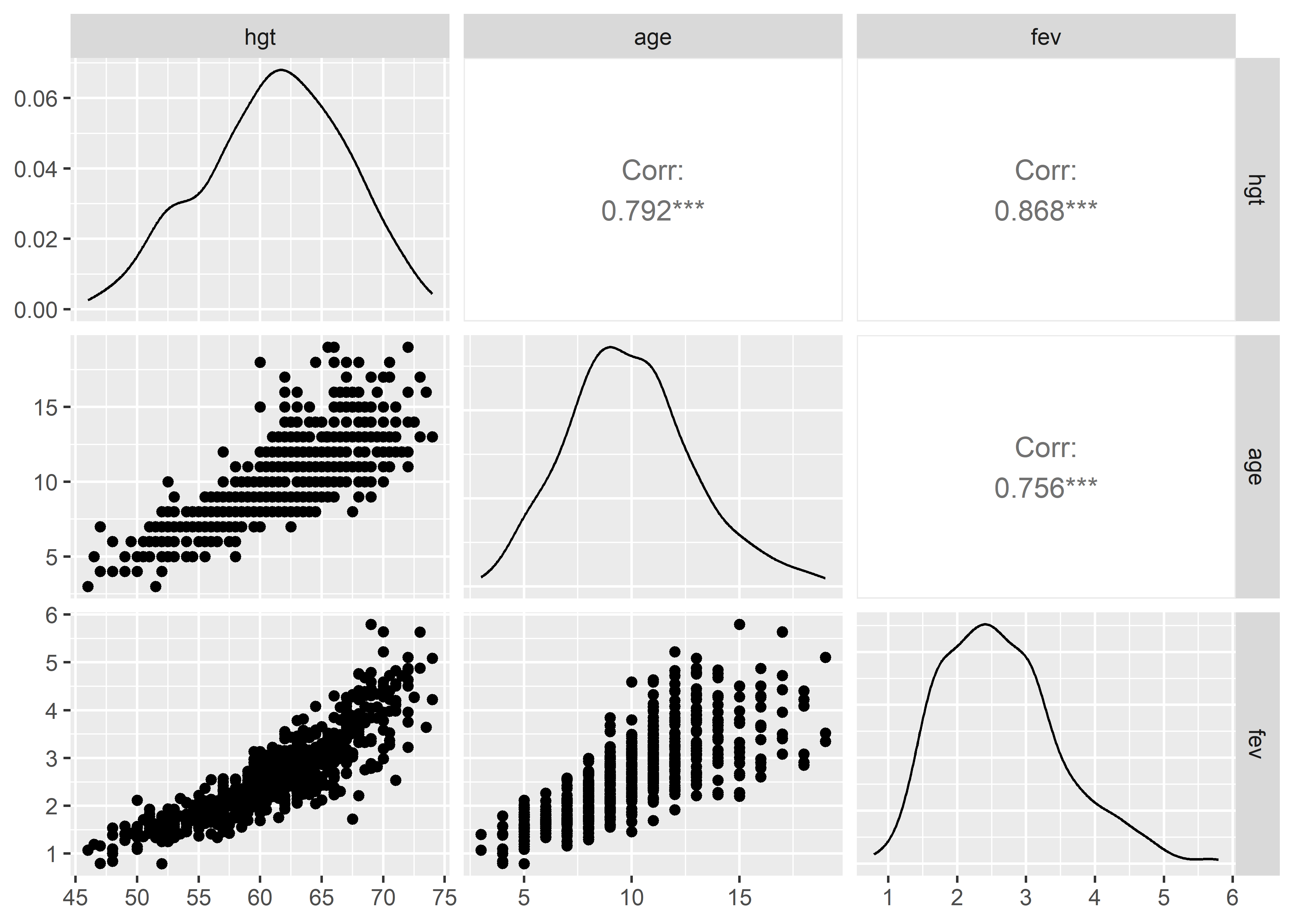
Los dos primeros gráficos de la última fila son los gráficos de dispersión de los predictores hgt y age versus fev. Podemos ver que la asociación entre age y fev es moderadamente lineal, aunque con menor fuerza que en el caso de hgt versus fev. Esto se puede comprobar con los valores del coeficiente de correlación de Pearson. La correlación entre hgt y fev es de 0.87, mientras que para age y fev es de 0.76.
12.3.1 Ajuste del modelo
Para decirle a la función lm() que incluya ambas variables predictoras en el modelo tenemos que escribir en el lado derecho de la formula el nombre de ambas variables separadas por el símbolo +:
fit_multiple <- lm(fev ~ hgt + age, data = fev)También podemos usar la función update() para modificar la fórmula del modelo de regresión simple fit_simple y que incluya la variable age además de la variable hgt que ya está incluida:
fit_multiple <- update(fit_simple, ~ . + age)El . en el segundo argumento de update() representa todo lo que ya está incluido en el modelo fit_simple.
Ahora, usamos la función summary() para ver un resumen del modelo:
summary(fit_multiple)
Call:
lm(formula = fev ~ hgt + age, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.50533 -0.25657 -0.01184 0.24575 2.01914
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.610466 0.224271 -20.558 < 2e-16 ***
hgt 0.109712 0.004716 23.263 < 2e-16 ***
age 0.054281 0.009106 5.961 4.11e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4197 on 651 degrees of freedom
Multiple R-squared: 0.7664, Adjusted R-squared: 0.7657
F-statistic: 1068 on 2 and 651 DF, p-value: < 2.2e-16Usando la función tidy() del paquete broom:
tidy(fit_multiple)# A tibble: 3 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -4.61 0.224 -20.6 9.46e-73
2 hgt 0.110 0.00472 23.3 1.38e-87
3 age 0.0543 0.00911 5.96 4.11e- 9Con las estimaciones de los parámetros, podemos escribir la ecuación de predicción del modelo de regresión lineal múltiple:
De la estimación del coeficiente de la altura podemos decir que se espera un aumento, en promedio, de 0.1097 L en el volumen espiratorio forzado de 0.1097 L por un aumento en la altura de una pulgada, manteniendo la edad constante. Por otro lado, podemos decir que se espera un aumento, en promedio, de 0.0543 en el volumen espiratorio forzado por un aumento de un año en la edad, manteniendo la altura constante.
12.3.2 Intervalos de confianza de los coeficientes
Usando la función tidy(), podemos hallar los intervalos de confianza de los coeficientes estimados:
tidy(fit_multiple, conf.int = TRUE)# A tibble: 3 × 7
term estimate std.error statistic p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -4.61 0.224 -20.6 9.46e-73 -5.05 -4.17
2 hgt 0.110 0.00472 23.3 1.38e-87 0.100 0.119
3 age 0.0543 0.00911 5.96 4.11e- 9 0.0364 0.0722El intervalo al 95% de confianza para el coeficiente estimado de la altura es
12.3.3 Coeficientes estandarizados
Debido a que los predictores se miden en diferentes unidades, es difícil comparar la magnitud del efecto de cada uno de estos en la respuesta. En este caso, la altura se mide en pulgadas y la edad en años. Si quisieramos comparar el efecto de estas variables, tendríamos que saber la equivalencia entre el cambio en una pulgada y el cambio en un año. Una técnica que se utiliza para comparar coeficientes en la misma escala, es estandarizar primero las variables antes de ajustar el modelo. Los coeficientes resultante se llaman coeficientes estandarizados y pueden ser usados para saber qué predictor tiene un mayor efecto relativo en la respuesta.
La estandarización de las variables consiste en transformar los valores de estas de manera que tengan promedio igual a 0 y desviación estándar igual a 1. Para lograr esto, se resta de cada valor el promedio original y se divide el resultado entre la desviación estándar original de la variable. Podemos hacer esto manualmente con los siguientes comandos:
fev_std <- fev %>%
mutate(
fev_std = (fev - mean(fev)) / sd(fev),
hgt_std = (hgt - mean(hgt)) / sd(hgt),
age_std = (age - mean(age)) / sd(age)
)
head(fev_std)# A tibble: 6 × 9
id age fev hgt sex smoke fev_std hgt_std age_std
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 301 9 1.71 57 0 0 -1.07 -0.726 -0.315
2 451 8 1.72 67.5 0 0 -1.05 1.11 -0.654
3 501 7 1.72 54.5 0 0 -1.06 -1.16 -0.992
4 642 9 1.56 53 1 0 -1.24 -1.43 -0.315
5 901 9 1.90 57 1 0 -0.856 -0.726 -0.315
6 1701 8 2.34 61 0 0 -0.347 -0.0252 -0.654También podemos usar la función scale(). Con el argumento center = TRUE le decimos a la función que reste el promedio de los valores y con el argumento scale = TRUE le decimos que divida por la desviación estándar de los valores:
fev_std <- fev %>%
mutate(
fev_std = scale(fev, center = TRUE, scale = TRUE),
hgt_std = scale(hgt, center = TRUE, scale = TRUE),
age_std = scale(age, center = TRUE, scale = TRUE)
)
head(fev_std)# A tibble: 6 × 9
id age fev hgt sex smoke fev_std[,1] hgt_std[,1] age_std[,1]
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 301 9 1.71 57 0 0 -1.07 -0.726 -0.315
2 451 8 1.72 67.5 0 0 -1.05 1.11 -0.654
3 501 7 1.72 54.5 0 0 -1.06 -1.16 -0.992
4 642 9 1.56 53 1 0 -1.24 -1.43 -0.315
5 901 9 1.90 57 1 0 -0.856 -0.726 -0.315
6 1701 8 2.34 61 0 0 -0.347 -0.0252 -0.654Ajustamos el modelo con las variables estandarizadas:
Call:
lm(formula = fev_std ~ hgt_std + age_std, data = fev_std)
Residuals:
Min 1Q Median 3Q Max
-1.73613 -0.29591 -0.01366 0.28343 2.32872
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.115e-17 1.893e-02 0.000 1
hgt_std 7.217e-01 3.102e-02 23.263 < 2e-16 ***
age_std 1.849e-01 3.102e-02 5.961 4.11e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4841 on 651 degrees of freedom
Multiple R-squared: 0.7664, Adjusted R-squared: 0.7657
F-statistic: 1068 on 2 and 651 DF, p-value: < 2.2e-16La estandarización de las variables hace que el intercepto estimado sea teóricamente igual a 0. Por otro lado, encontramos que el coeficiente estandarizado de la altura es
El problema de los coeficientes estandarizados, evidentemente, es que la interpretación no se hace sobre las variables originales, sino sobre las variables transformadas. Una forma de aliviar este problema, es solo estandarizando los predictores. Además, hay que tener cuidado en concluir que la altura es más importante que la edad para predecir el volumen espiratorio forzado, ya que los coeficientes estandarizados dependen del rango de los predictores y si sacamos otra muestra con rangos diferentes es probable que encontremos resultados diferentes (Montgomery, Peck, y Vining 2013).
Existen funciones que calculan los coeficientes estimados sin que el usuario tenga que estandarizar manualmente los predictores. Una de estas es la función model_parameters() del paquete parameters. Esta permite tener un resumen de las estimaciones del modelo, al igual que lo hace summary() y tidy(). Por ejemplo, para el modelo sin estandarización:
model_parameters(fit_multiple)Parameter | Coefficient | SE | 95% CI | t(651) | p
-----------------------------------------------------------------------
(Intercept) | -4.61 | 0.22 | [-5.05, -4.17] | -20.56 | < .001
hgt | 0.11 | 4.72e-03 | [ 0.10, 0.12] | 23.26 | < .001
age | 0.05 | 9.11e-03 | [ 0.04, 0.07] | 5.96 | < .001
Uncertainty intervals (equal-tailed) and p-values (two-tailed) computed
using a Wald t-distribution approximation.model_parameters() devuelve un data frame, sin embargo, imprime una tabla más estética. Para visualizar el data frame, podemos convertirlo a un objeto tibble:
fit_multiple %>%
model_parameters() %>%
as_tibble()# A tibble: 3 × 9
Parameter Coefficient SE CI CI_low CI_high t df_error p
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl>
1 (Intercept) -4.61 0.224 0.95 -5.05 -4.17 -20.6 651 9.46e-73
2 hgt 0.110 0.00472 0.95 0.100 0.119 23.3 651 1.38e-87
3 age 0.0543 0.00911 0.95 0.0364 0.0722 5.96 651 4.11e- 9A diferencia de las funciones que vimos previamente, model_parameters() también permite calcular los coeficientes estandarizados. Para esto, necesitamos añadir el argumento standardize = "refit":
model_parameters(fit_multiple, standardize = "refit")Parameter | Coefficient | SE | 95% CI | t(651) | p
---------------------------------------------------------------------
(Intercept) | -1.43e-16 | 0.02 | [-0.04, 0.04] | -7.53e-15 | > .999
hgt | 0.72 | 0.03 | [ 0.66, 0.78] | 23.26 | < .001
age | 0.18 | 0.03 | [ 0.12, 0.25] | 5.96 | < .001
Uncertainty intervals (equal-tailed) and p-values (two-tailed) computed
using a Wald t-distribution approximation.Si queremos que no se estandarice la respuesta, incluimos el arguemento include_response = FALSE:
model_parameters(fit_multiple, standardize = "refit", include_response = FALSE)Parameter | Coefficient | SE | 95% CI | t(651) | p
-----------------------------------------------------------------
(Intercept) | 2.64 | 0.02 | [2.60, 2.67] | 160.66 | < .001
hgt | 0.63 | 0.03 | [0.57, 0.68] | 23.26 | < .001
age | 0.16 | 0.03 | [0.11, 0.21] | 5.96 | < .001
Uncertainty intervals (equal-tailed) and p-values (two-tailed) computed
using a Wald t-distribution approximation.De esta manera, podemos interpretar los coeficientes estandarizados como los cambios en la respuesta en su escala original cuando los predictores estandarizados cambian en una unidad, dado que el otro predictor se mantiene constante.
12.3.3.1 Forest plots
Un forest plot es un gráfico que muestra la estimación puntual y el intervalo de confianza de los coeficientes de un modelo. El paquete see tiene una función genérica llamada plot() para graficar los resultados producidos por la función model_parameters() del paquete parameters. Primero, es necesario llamar al paquete see:
fit_multiple %>%
model_parameters() %>%
plot()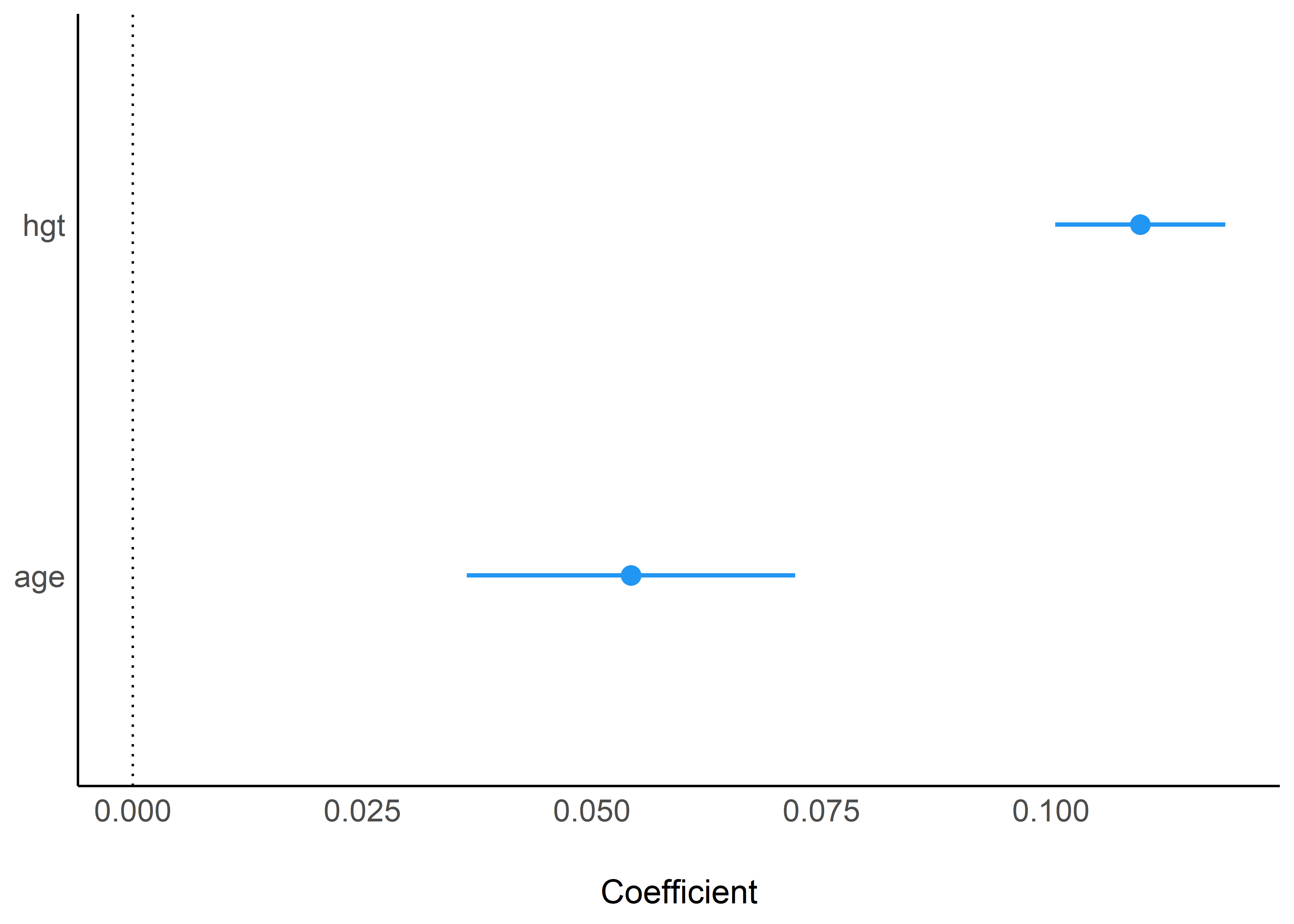
Estandarizando los coeficientes:
fit_multiple %>%
model_parameters(standardize = "refit") %>%
plot()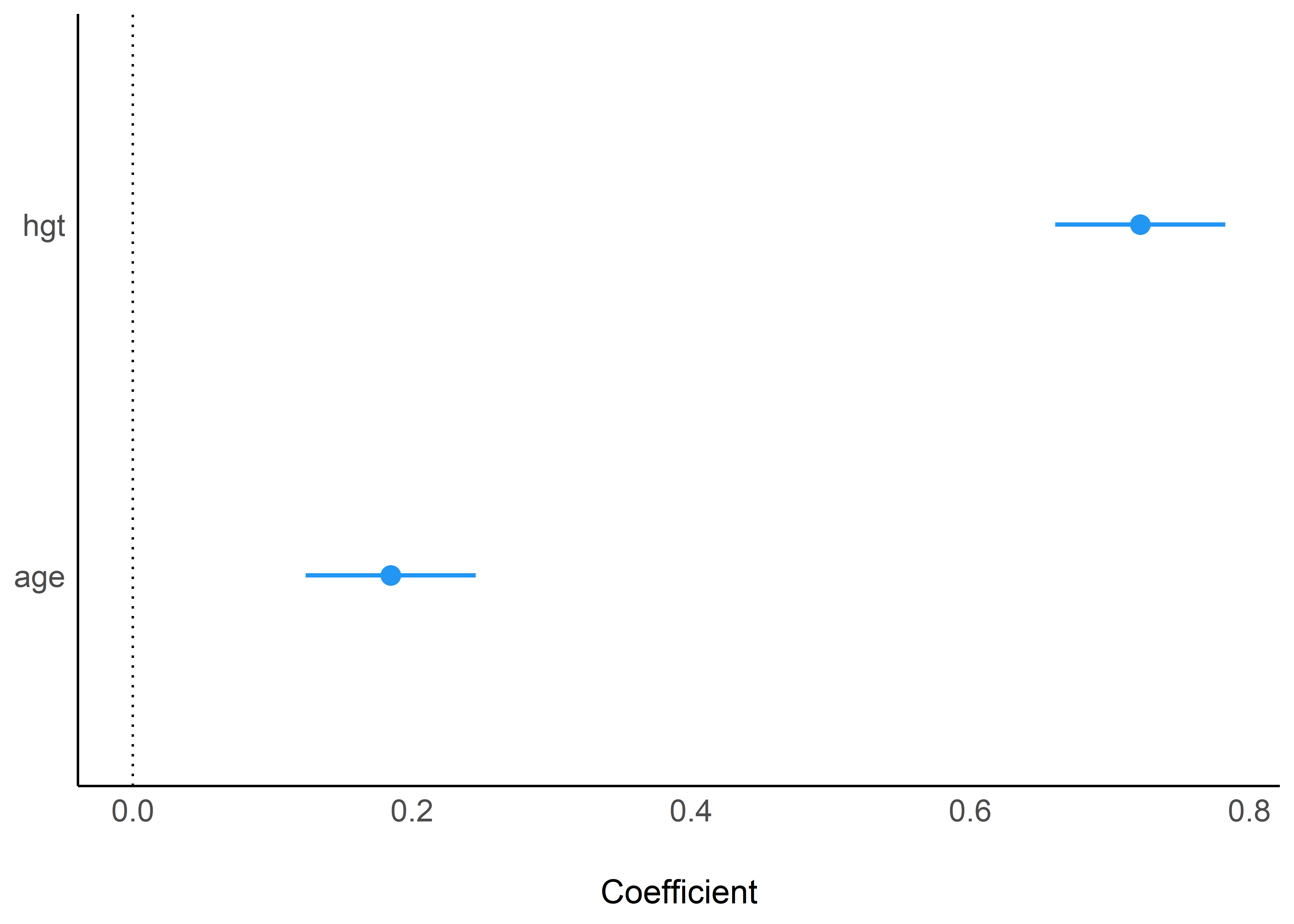
En este último gráfico podemos ver con mayor claridad la diferencia en magnitud de los efectos de la altura y la edad en el volumen espiratorio forzado (estandarizados).
Podemos, además, agregar los valores de los coeficientes y los intervalos de confianza añadiendo el argumento show_labels = TRUE:
fit_multiple %>%
model_parameters(standardize = "refit") %>%
plot(show_labels = TRUE)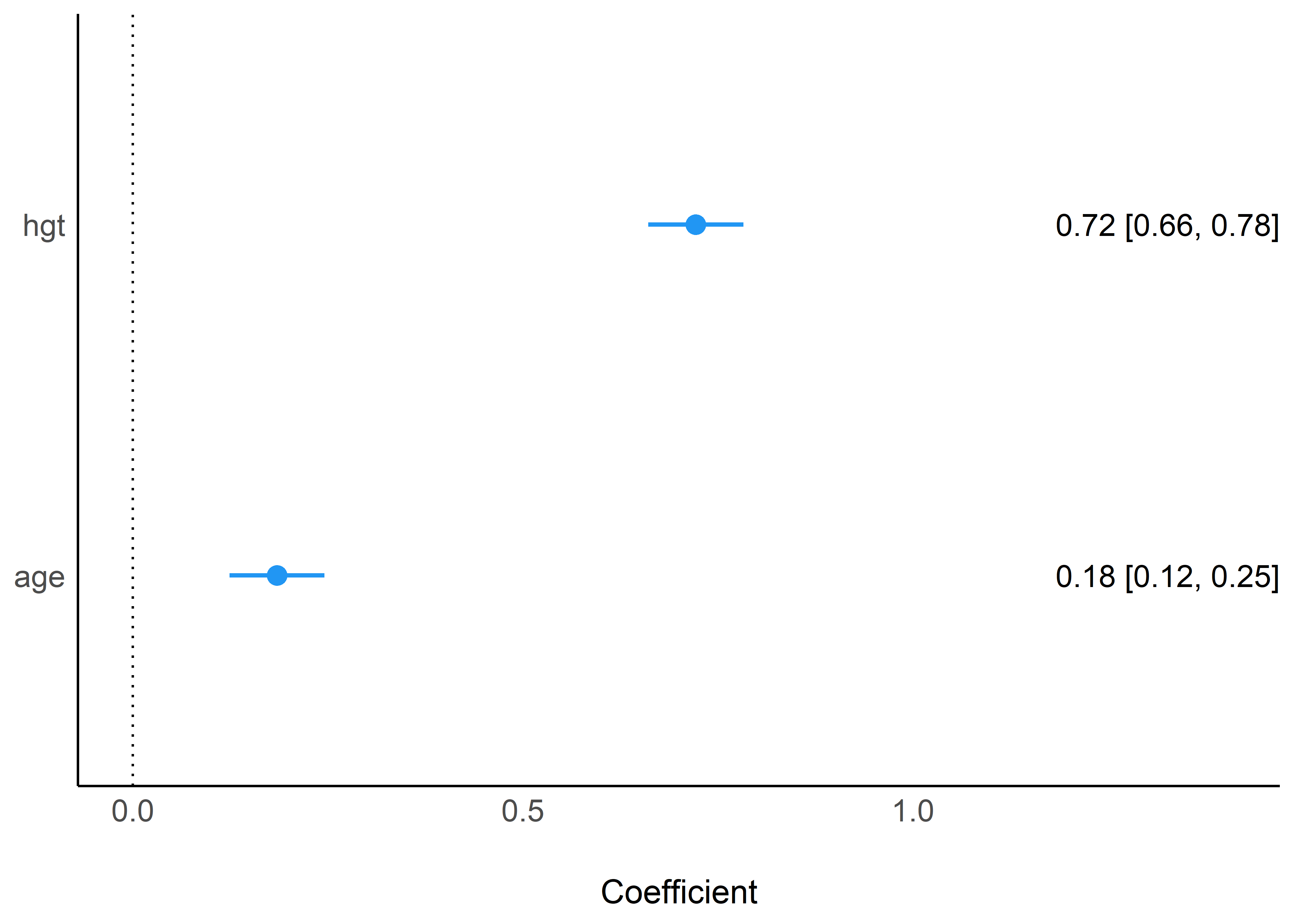
12.3.4 Predicción de la respuesta
Podemos usar la función augment() del paquete broom para hallar los valores predichos del modelo ajustado de regresión múltiple. Por ejemplo, para las primeras 5 observaciones de la data:
augment(fit_multiple)[1:5,]# A tibble: 5 × 9
fev hgt age .fitted .resid .hat .sigma .cooksd .std.resid
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1.71 57 9 2.13 -0.424 0.00262 0.420 0.000893 -1.01
2 1.72 67.5 8 3.23 -1.51 0.0131 0.416 0.0578 -3.61
3 1.72 54.5 7 1.75 -0.0288 0.00363 0.420 0.00000573 -0.0687
4 1.56 53 9 1.69 -0.135 0.00738 0.420 0.000258 -0.322
5 1.90 57 9 2.13 -0.237 0.00262 0.420 0.000279 -0.565 En el caso de que tuvieramos un conjunto nuevo de valores de los predictores para los cuales queremos hacer la predicción de la respuesta, los pasamos como un data frame al parámetro newdata:
set.seed(2023)
new_data_multiple <- tibble(
hgt = runif(n = 5, min = min(fev$hgt), max = max(fev$hgt)),
age = runif(n = 5, min = min(fev$age), max = max(fev$age))
)
augment(fit_multiple, newdata = new_data_multiple)# A tibble: 5 × 3
hgt age .fitted
<dbl> <dbl> <dbl>
1 59.1 4.93 2.14
2 55.4 9.82 2.00
3 50.6 12.9 1.64
4 57.1 7.21 2.04
5 46.9 10.6 1.1112.3.4.1 Incertidumbre de valores predichos
Podemos también calcular los intervalos de confianza o de predicción de los valores predichos, dependiendo de si queremos estimar el valor medio de la distribución de la respuesta o si queremos predecir un caso individual de la respuesta, respectivamente.
En la función tidy() del paquete broom, podemos añadir el argumento interval = "confidence" para hallar los intervalos de confianza al 95%:
augment(fit_multiple, newdata = new_data_multiple, interval = "confidence")# A tibble: 5 × 5
hgt age .fitted .lower .upper
<dbl> <dbl> <dbl> <dbl> <dbl>
1 59.1 4.93 2.14 2.06 2.22
2 55.4 9.82 2.00 1.94 2.06
3 50.6 12.9 1.64 1.49 1.78
4 57.1 7.21 2.04 2.00 2.09
5 46.9 10.6 1.11 0.960 1.25O, en su defecto, interval = "prediction" para los intervalos de predicción:
augment(fit_multiple, newdata = new_data_multiple, interval = "prediction")# A tibble: 5 × 5
hgt age .fitted .lower .upper
<dbl> <dbl> <dbl> <dbl> <dbl>
1 59.1 4.93 2.14 1.31 2.97
2 55.4 9.82 2.00 1.17 2.83
3 50.6 12.9 1.64 0.799 2.47
4 57.1 7.21 2.04 1.22 2.87
5 46.9 10.6 1.11 0.269 1.94A su vez, también podemos usar las funciones estimate_expectation() y estimate_prediction() del paquete modelbased. Para los intervalos de confianza:
estimate_expectation(fit_multiple, data = new_data_multiple)Model-based Expectation
hgt | age | Predicted | SE | 95% CI
-----------------------------------------------
59.07 | 4.93 | 2.14 | 0.04 | [2.06, 2.22]
55.39 | 9.82 | 2.00 | 0.03 | [1.94, 2.06]
50.56 | 12.89 | 1.64 | 0.07 | [1.49, 1.78]
57.09 | 7.21 | 2.04 | 0.02 | [2.00, 2.09]
46.85 | 10.62 | 1.11 | 0.07 | [0.96, 1.25]
Variable predicted: fevPara los intervalos de predicción:
estimate_prediction(fit_multiple, data = new_data_multiple)Model-based Prediction
hgt | age | Predicted | SE | 95% CI
-----------------------------------------------
59.07 | 4.93 | 2.14 | 0.42 | [1.31, 2.97]
55.39 | 9.82 | 2.00 | 0.42 | [1.17, 2.83]
50.56 | 12.89 | 1.64 | 0.43 | [0.80, 2.47]
57.09 | 7.21 | 2.04 | 0.42 | [1.22, 2.87]
46.85 | 10.62 | 1.11 | 0.43 | [0.27, 1.94]
Variable predicted: fev12.4 Predictores categóricos
Hasta ahora hemos visto cómo ajustar modelos de regresión lineal en R usando predictores de naturaleza continua. Si quisiéramos utilizar un predictor categórico, lo recomendable en R es primero transformar la variable en un objeto tipo factor usando la función factor(). Por ejemplo, la variable sex del conjunto de datos fev es el sexo de cada niño o niña en la muestra codificado como 1 si es hombre o 0 si es mujer. A esta codificación se le conoce como codificación dummy. Si bien es posible ajustar un modelo usando esta codificación, es una buena práctica transformar primero la variable en factor para tener mayor control de los niveles y definir cuál es el de referencia, sobre todo cuando la variable posee más de dos niveles. Para el ajuste del modelo, R se encarga internamente de codificar la variable.
Transformemos la variable sex en factor:
Ahora, ajustemos un modelo con sex como predictor:
Call:
lm(formula = fev ~ sex, data = fev)
Residuals:
Min 1Q Median 3Q Max
-2.01645 -0.69420 -0.06367 0.58233 2.98055
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.45117 0.04759 51.505 < 2e-16 ***
sexHombre 0.36128 0.06640 5.441 7.5e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8487 on 652 degrees of freedom
Multiple R-squared: 0.04344, Adjusted R-squared: 0.04197
F-statistic: 29.61 on 1 and 652 DF, p-value: 7.496e-08Según estos resultados, los hombres tienen un volumen espiratorio forzado promedio mayor que las mujeres por 0.3613 L.
12.4.1 Medias marginales
Podemos obtener la media de la variable de respuesta para cada nivel del predictor categorico usando la función estimate_means() del paquete modelbased. Con el parámetro at de esta función podemos especificar la variable para la cual se van a calcular las medias marginales:
estimate_means(fit_categorical, at = "sex")Estimated Marginal Means
sex | Mean | SE | 95% CI
-----------------------------------
Mujer | 2.45 | 0.05 | [2.36, 2.54]
Hombre | 2.81 | 0.05 | [2.72, 2.90]
Marginal means estimated at sexSi sustraemos de la media del grupo de hombre la media del grupo de mujeres obtenemos sex. Cabe resaltar que la media marginal de las mujeres es el valor del intercepto del modelo.
En este modelo sencillo, las medias marginales estimadas equivalen a los promedios muestrales de la variable fev calculados en cada grupo de la variable sex:
# A tibble: 2 × 2
sex fev_mean
<fct> <dbl>
1 Mujer 2.45
2 Hombre 2.81La función plot() del paquete see genera un gráfico sencillo de los resultados de la función estimate_means() que muestra las medias marginales de cada grupo (recordar siempre llamar antes al paquete see):
fit_categorical %>%
estimate_means(at = "sex") %>%
plot()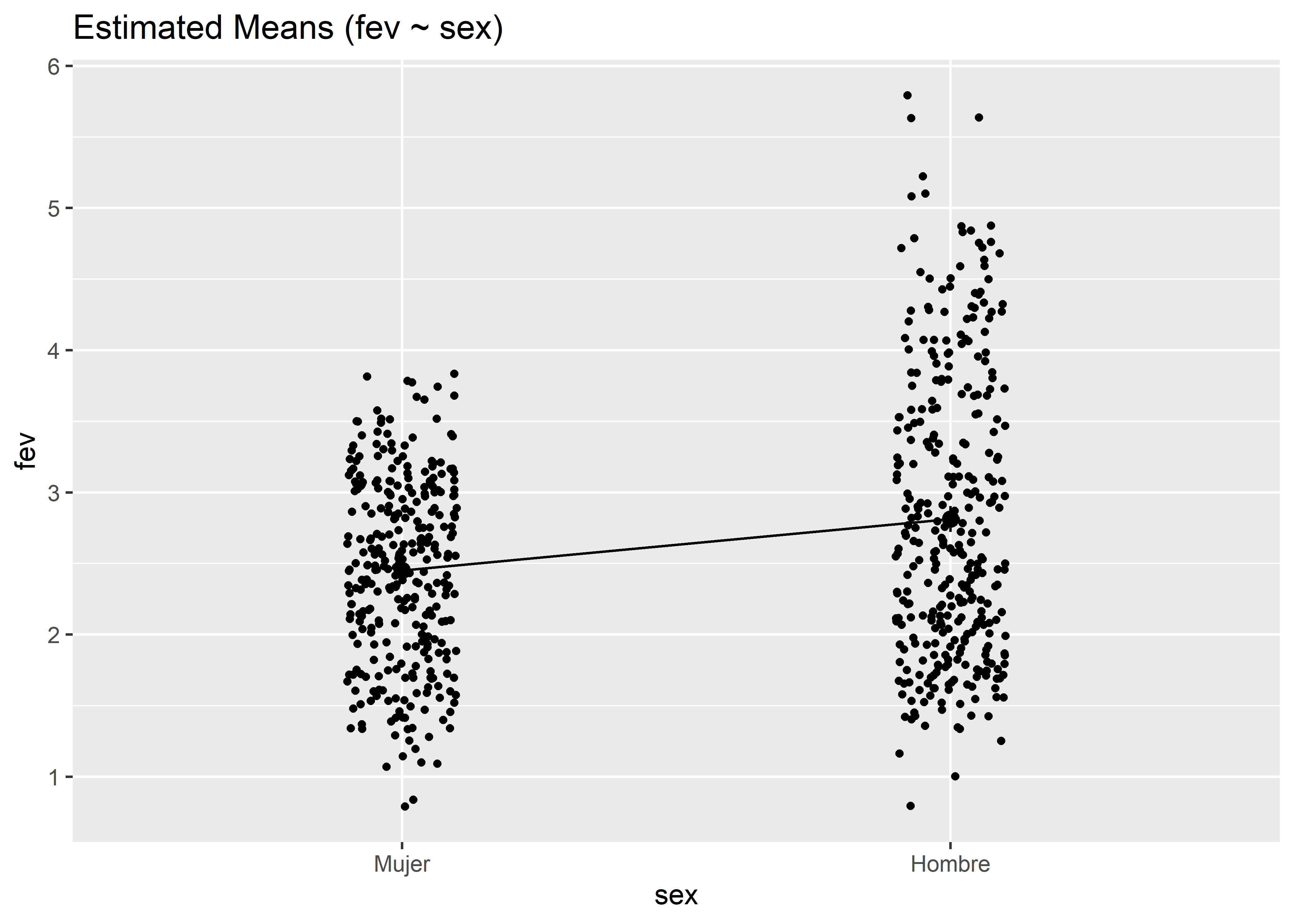
Para graficar los intervalos de confianza, podemos usar la función geom_pointrange() del paquete ggplot2:
fit_categorical %>%
estimate_means(at = "sex") %>%
ggplot(aes(x = sex, y = Mean)) +
geom_line(aes(group = "x")) +
geom_pointrange(aes(color = sex, ymin = CI_low, ymax = CI_high))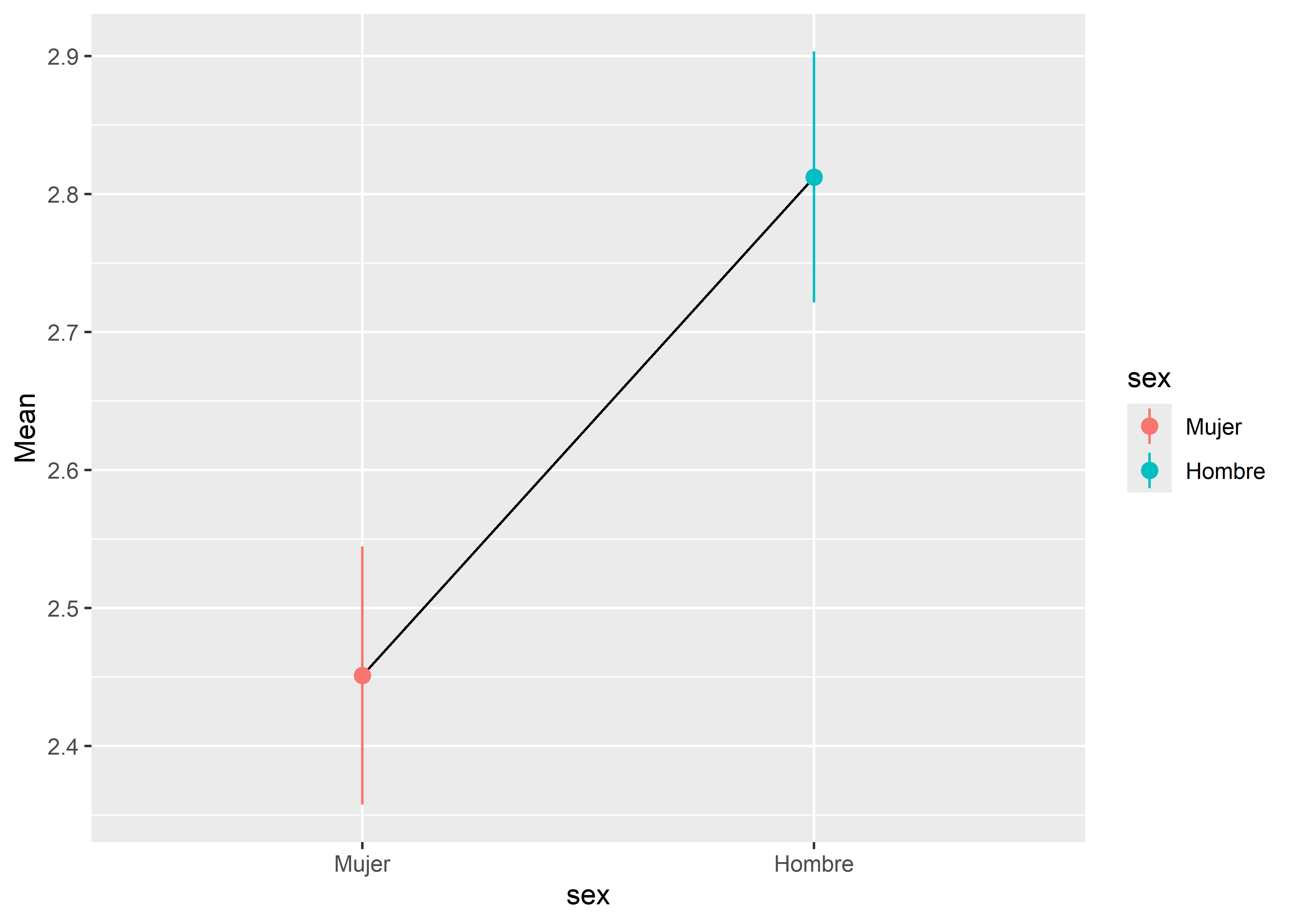
Podemos también estimar un modelo de regresión lineal múltiple que incluya a la variable categórica sex. Por ejemplo, incluyamos en un modelo a hgt y sex:
Call:
lm(formula = fev ~ hgt + sex, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.6763 -0.2505 0.0001 0.2347 2.0722
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.390263 0.180082 -29.932 < 2e-16 ***
hgt 0.130231 0.002964 43.933 < 2e-16 ***
sexHombre 0.125123 0.033801 3.702 0.000232 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4265 on 651 degrees of freedom
Multiple R-squared: 0.7587, Adjusted R-squared: 0.758
F-statistic: 1024 on 2 and 651 DF, p-value: < 2.2e-16La ecuación de predicción para este modelo es
Pasando la variable categórica a codificación dummy, tenemos que para las mujeres (
Este modelo, entonces, genera dos ecuaciones de predicción del volumen espiratorio forzado dada la altura, una para los hombres y otra para las mujeres, con pendientes iguales pero interceptos diferentes. Para visualizar las líneas de regresión para cada grupo, podemos primero generar una grilla de valores predichos y sus respectivos intervalos de confianza con la función estimate_relation() del paquete modelbased, y luego usar la función plot() del paquete see:
fit_same_slope %>%
estimate_relation() %>%
plot()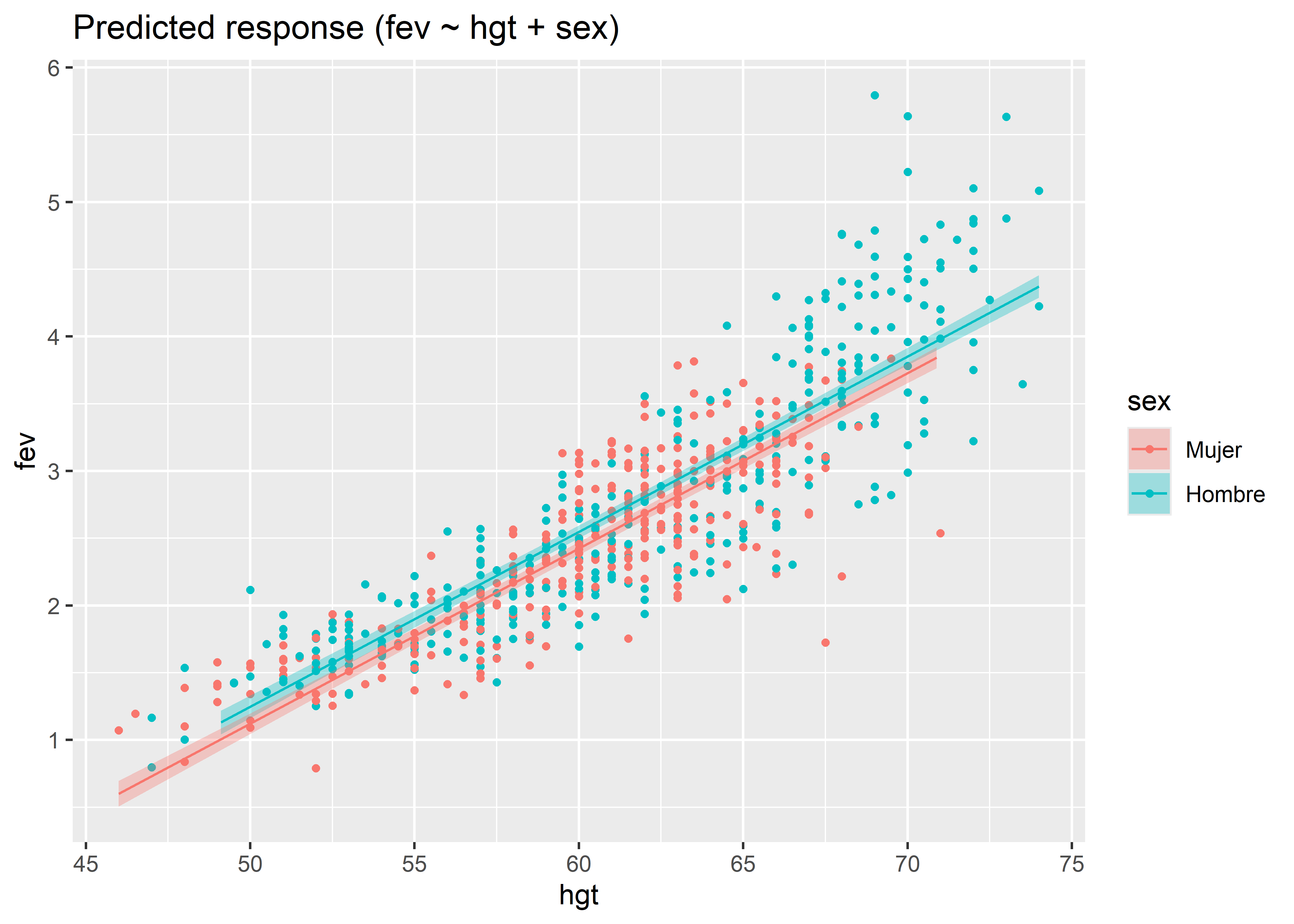
También podemos estimar las medias marginales de los grupos de la variable categórica sex dado que hgt también está en el modelo:
estimate_means(fit_same_slope, at = "sex")Estimated Marginal Means
sex | Mean | SE | 95% CI
-----------------------------------
Mujer | 2.57 | 0.02 | [2.53, 2.62]
Hombre | 2.70 | 0.02 | [2.65, 2.74]
Marginal means estimated at sexVemos que las medias marginales son diferentes a las del modelo que solo incluía sex. Esto es esperable ya que ahora también estamos ajustando por otra variable. Las medias marginales se calculan controlando el efecto del otro predictor. En este caso, el control se hace manteniendo constante al otro predictor continuo en su valor promedio.
12.4.2 Contrastes
Si queremos contrastar entre las medias marginales de los niveles de la variable predictora, podemos usar la función estimate_contrasts() del paquete modelbased. Por ejemplo, para el modelo con solo el predictor sex:
estimate_contrasts(fit_categorical, contrast = "sex")Marginal Contrasts Analysis
Level1 | Level2 | Difference | 95% CI | SE | t(652) | p
----------------------------------------------------------------------
Mujer | Hombre | -0.36 | [-0.49, -0.23] | 0.07 | -5.44 | < .001
Marginal contrasts estimated at sex
p-value adjustment method: Holm (1979)Podemos ver que el contraste entre la media marginal de fev del grupo de mujeres y del grupo de hombres es estadísticamente significativo. Por defecto, el método de ajuste de comparaciones múltiples es el método de Holm-Bonferroni. Otros métodos pueden usarse, como el método de Tukey ("tukey") o el método de Bonferroni ("bonferroni").
Para el modelo con hgt y sex como predictores:
estimate_contrasts(fit_same_slope, contrast = "sex")Marginal Contrasts Analysis
Level1 | Level2 | Difference | 95% CI | SE | t(651) | p
----------------------------------------------------------------------
Mujer | Hombre | -0.13 | [-0.19, -0.06] | 0.03 | -3.70 | < .001
Marginal contrasts estimated at sex
p-value adjustment method: Holm (1979)Vemos que en este caso el constraste también es significativo.
12.5 Interacciones
Veamos ahora cómo agregar términos de interacción en un modelo de regresión lineal en R. Existen dos formas para incluir interacciones. La primera es usando el operador *. Ajustemos un modelo con el término de interacción entre hgt y sex::
Call:
lm(formula = fev ~ hgt * sex, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.54654 -0.25282 0.00649 0.25666 2.00491
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.318219 0.297637 -14.508 < 2e-16 ***
hgt 0.112426 0.004928 22.815 < 2e-16 ***
sexHombre -1.545629 0.373843 -4.134 4.02e-05 ***
hgt:sexHombre 0.027457 0.006119 4.487 8.54e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4204 on 650 degrees of freedom
Multiple R-squared: 0.766, Adjusted R-squared: 0.7649
F-statistic: 709.2 on 3 and 650 DF, p-value: < 2.2e-16La ecuación de predicción para este modelo es
Pasando la variable categórica a codificación dummy, tenemos que para las mujeres (
mientras que para los hombres (
Entonces, con la interacción se generan dos ecuaciones de predicción del volumen espiratorio forzado dada la altura, una para los hombres y otra para las mujeres, con pendientes e interceptos diferentes. Para visualizar las líneas de regresión para cada grupo, podemos usar la función estimate_relation() del paquete modelbased, y luego usar la función plot() del paquete see:
fit_interaction %>%
estimate_relation() %>%
plot()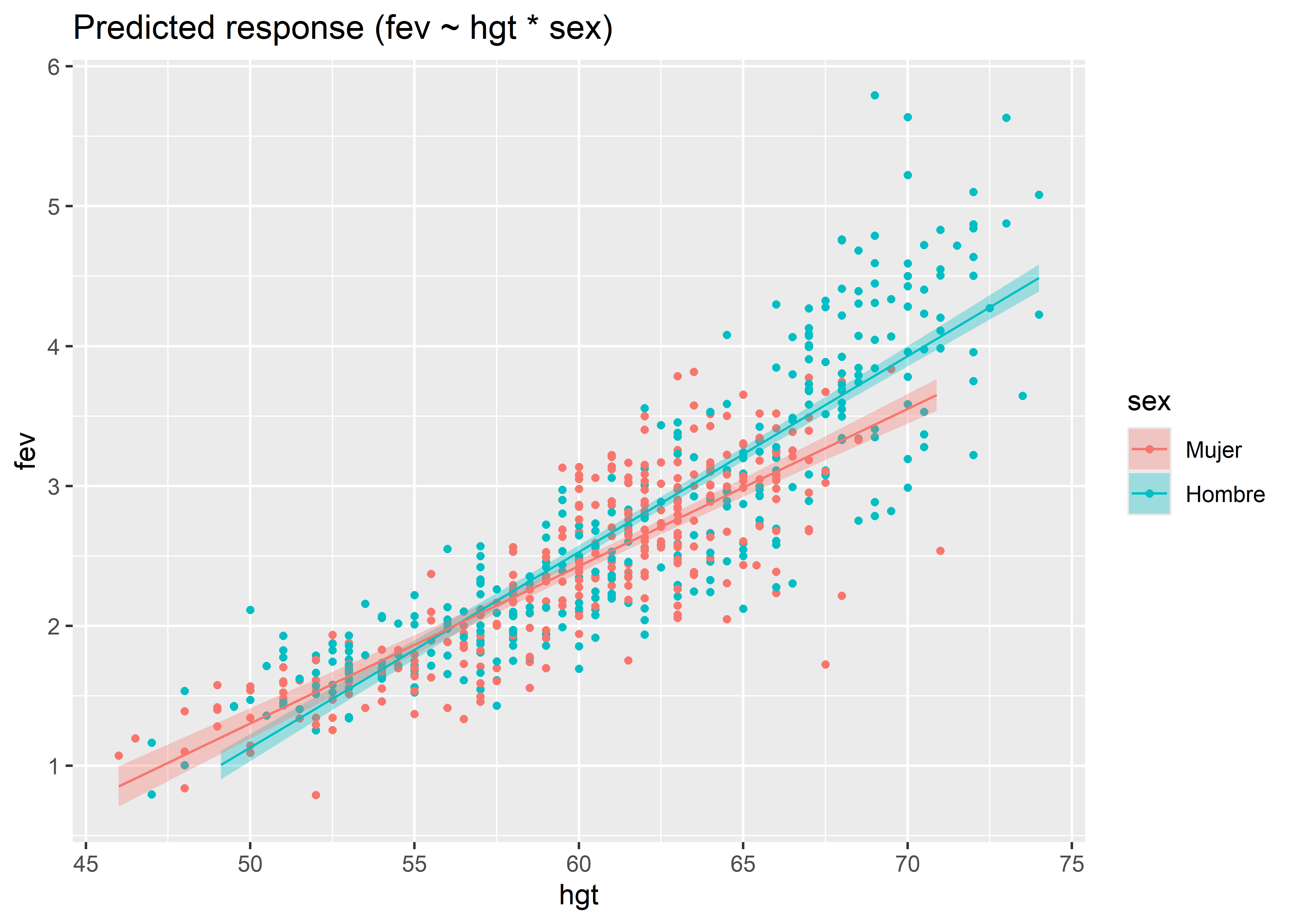
Otra forma de incluir una interacción en el modelo es usando el operador :. Este operador solo incluye el término de interacción hgt:sex, por lo que debemos agregar los otros términos explícitamente:
Call:
lm(formula = fev ~ hgt + sex + hgt:sex, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.54654 -0.25282 0.00649 0.25666 2.00491
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.318219 0.297637 -14.508 < 2e-16 ***
hgt 0.112426 0.004928 22.815 < 2e-16 ***
sexHombre -1.545629 0.373843 -4.134 4.02e-05 ***
hgt:sexHombre 0.027457 0.006119 4.487 8.54e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4204 on 650 degrees of freedom
Multiple R-squared: 0.766, Adjusted R-squared: 0.7649
F-statistic: 709.2 on 3 and 650 DF, p-value: < 2.2e-16Una última forma de incluir los efectos principales e interacciones es usando el operador ^ para especificar hasta qué orden de interacción se debe incluir. Por ejemplo, (hgt + sex)^2 va a incluir los términos de hgt y sex hasta el segundo grado de interacción (interacción en pares):
Call:
lm(formula = fev ~ (hgt + sex)^2, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.54654 -0.25282 0.00649 0.25666 2.00491
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.318219 0.297637 -14.508 < 2e-16 ***
hgt 0.112426 0.004928 22.815 < 2e-16 ***
sexHombre -1.545629 0.373843 -4.134 4.02e-05 ***
hgt:sexHombre 0.027457 0.006119 4.487 8.54e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4204 on 650 degrees of freedom
Multiple R-squared: 0.766, Adjusted R-squared: 0.7649
F-statistic: 709.2 on 3 and 650 DF, p-value: < 2.2e-1612.5.1 Efectos marginales
Podemos querer saber cuál es el efecto promedio de hgt en cada grupo de sex, es decir, el efecto marginal de hgt en el modelo. Para calcular los efectos marginales de un predictor sobre los niveles o valores de otro, podemos usar la función estimate_slopes() del paquete modelbased. Para especificar para qué predictor se van a calcular los efectos marginales usamos el parámetro trend, mientras que para especificar sobre qué predictor calcular los efectos marginales se utiliza el parámetro at:
estimate_slopes(fit_interaction, trend = "hgt", at = "sex")Estimated Marginal Effects
sex | Coefficient | SE | 95% CI | t(650) | p
----------------------------------------------------------------
Mujer | 0.11 | 4.93e-03 | [0.10, 0.12] | 22.82 | < .001
Hombre | 0.14 | 3.63e-03 | [0.13, 0.15] | 38.55 | < .001
Marginal effects estimated for hgtVemos que el efecto marginal, es decir, el cambio promedio en el volumen espiratorio forzado por un aumento en la altura de una pulgada en el grupo de las mujeres es de 0.11 L, mientras que en el grupo de hombres es de 0.14 L. Para graficar estos resultados podemos usar la función plot() del paquete see:
fit_interaction %>%
estimate_slopes(trend = "hgt", at = "sex") %>%
plot()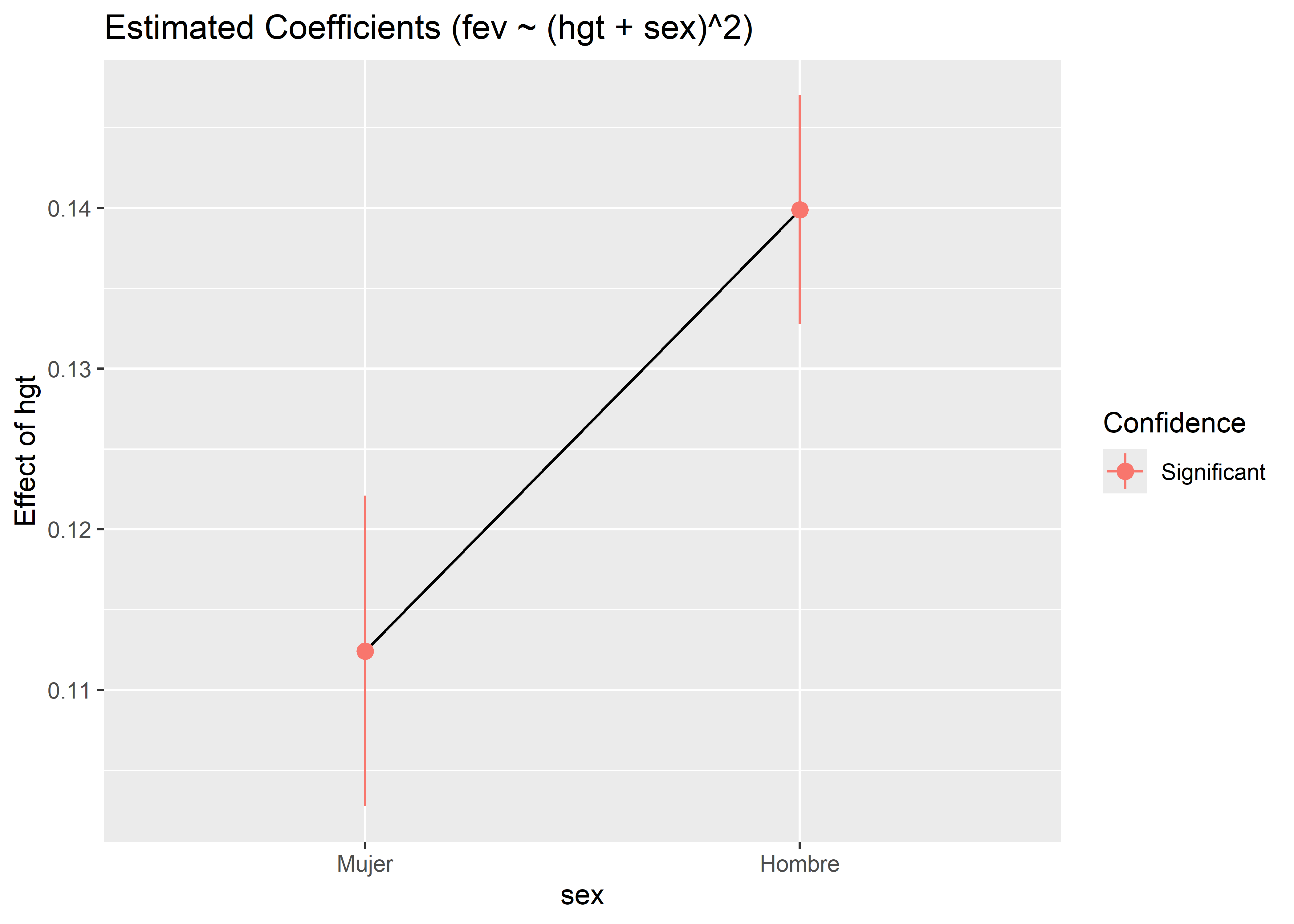
Este gráfico también nos indica si los efectos marginales son significativos.
12.5.2 Interacción entre dos predictores continuos
Vimos en la sección anterior la interacción entre hgt y sex, siendo el primero un predictor continuo y el segundo uno categórico. Veamos ahora la interacción entre dos predictores continuos, hgt y age.
Call:
lm(formula = fev ~ hgt * age, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.64871 -0.23420 0.01321 0.21743 1.80869
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.6636068 0.5098915 -1.301 0.194
hgt 0.0458080 0.0087359 5.244 2.13e-07 ***
age -0.4181823 0.0561327 -7.450 2.99e-13 ***
hgt:age 0.0074975 0.0008801 8.518 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3984 on 650 degrees of freedom
Multiple R-squared: 0.7899, Adjusted R-squared: 0.7889
F-statistic: 814.4 on 3 and 650 DF, p-value: < 2.2e-16Vemos que la interacción resulta significativa. Sin embargo, resulta complicado interpretar esta interacción. En el caso de la interacción entre hgt y sex era sencillo ya que comparábamos el efecto de la altura entre mujeres y hombres. Sin embargo, tanto hgt y age toman muchos valores. ¿Sobre qué combinaciones de valores deberíamos analizar la interacción?
Una opción para interpretar la interacción entre predictores continuos es usando intervalos de Johnson-Neyman. Un intervalo de Jonson-Neyman nos dice el rango de valores de un predictor, llamada variable moderadora, para los cuales el efecto del otro predictor en la interacción, llamado variable focal, es significativo. Por ejemplo, usemos como variable moderadora la altura y como variable focal la edad. Para calcular el intervalo podemos usar la función johnson_neyman() del paquete interactions.
El primer parámetro de johnson_neyman() es el modelo. Luego, pasamos la variable focal en el parámetro pred y la variable moderadora en el parámetro modx:
johnson_neyman(fit_interact_continuous, pred = age, modx = hgt)JOHNSON-NEYMAN INTERVAL
When hgt is OUTSIDE the interval [52.45, 58.29], the slope of age is p <
.05.
Note: The range of observed values of hgt is [46.00, 74.00]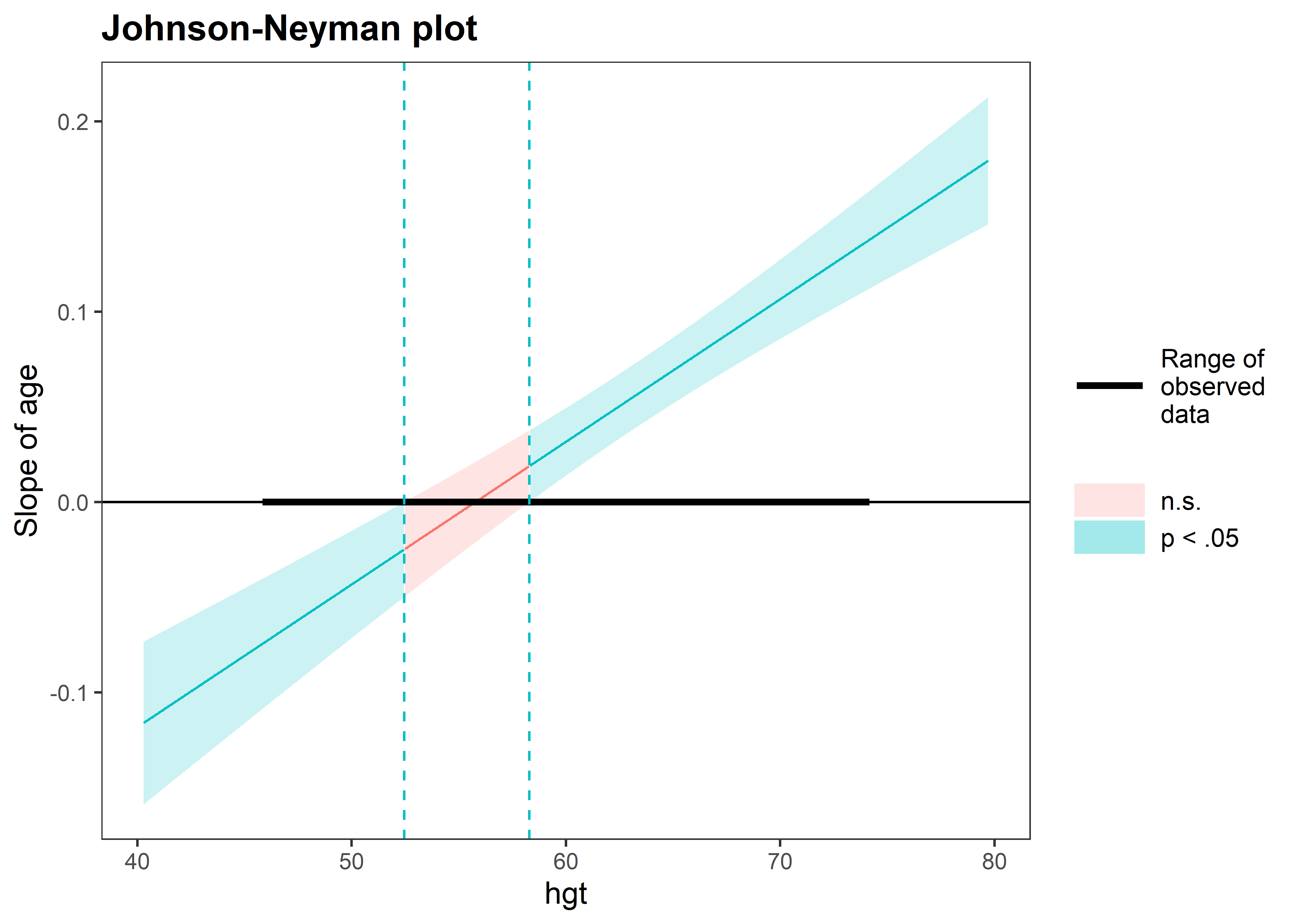
La función nos imprime un mensaje con el intervalo de Johnson-Neyman y su interpretación. En este caso nos dice que el efecto de age es significativo (a un nivel de significancia de 0.05) cuando hgt está fuera del intervalo [52.23, 58.41]. Además, también genera un gráfico donde podemos visualizar el intervalo sobre hgt y las zonas de significancia para el efecto marginal de age.
Un problema con este método es que para encontrar el intervalo de la variable moderadora donde la variable focal es significativa se tienen que hacer comparaciones múltiples sobre varios potenciales intervalos y, si no se corrige por la tasa de descubrimientos falso, podríamos obtener un resultado engañoso. Para corregir el nivel de significancia por las comparaciones múltiples, podemos agregar el argumento control.fdr = TRUE:
johnson_neyman(fit_interact_continuous, pred = age, modx = hgt, control.fdr = TRUE)JOHNSON-NEYMAN INTERVAL
When hgt is OUTSIDE the interval [52.23, 58.41], the slope of age is p <
.05.
Note: The range of observed values of hgt is [46.00, 74.00]
Interval calculated using false discovery rate adjusted t = 2.07 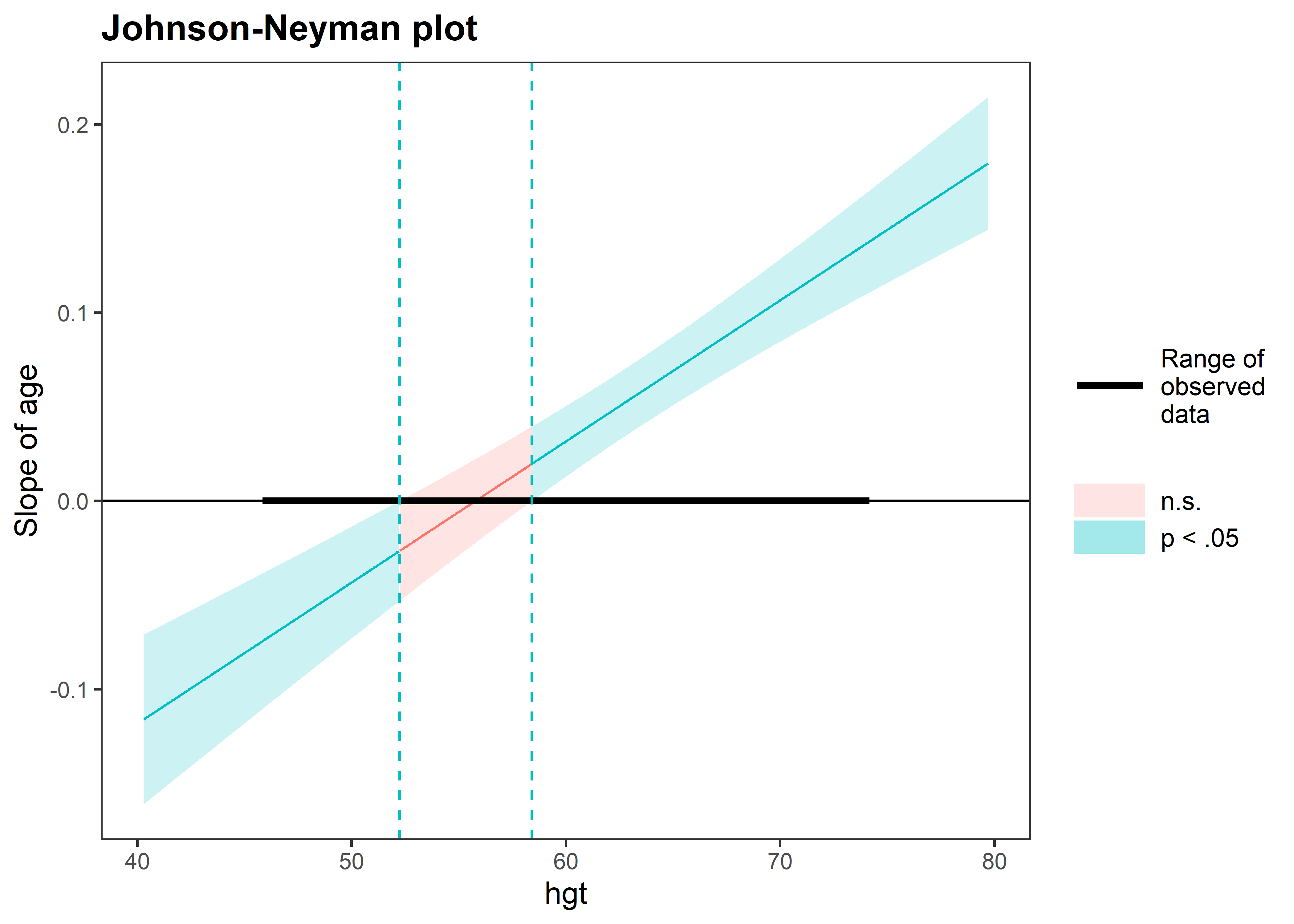
Vemos que el intervalo de Jonson-Neyman pasó de ser [52.45, 58.29] sin corrección a [52.23, 58.41] con correción. Generalmente, los intervalos con correción suelen ser más conservadores (más amplios).
12.6 Ejercicios
El archivo de datos iq.csv contiene los puntajes obtenidos en pruebas cognitivas (IQ tests) de niños pre-escolares, además de los datos sobre algunas carácterísticas de las madres como si la madre se graduó o no de la secundaria, el puntaje de la prueba cognitiva de la madre, el estatus ocupacional de la madre durante los primeros años de vida del niño, y la edad de la madre. Para mayor detalle sobre las variables ver el diccionario de datos en Anexos.
Este conjunto de datos es una submuestra de una encuesta realizada a mujeres adultas y sus niños en Estados Unidos. El archivo fue descargado del repositorio de código y datos del libro de Gelman, Hill, y Vehtari (2020) que se encuentra en este enlace.
Ejercicio 1
Construir un modelo de regresión lineal simple para los puntajes de la prueba cognitiva de los niños usando el puntaje de la madre como predictor. Obtener el intervalo al 97% de confianza del coeficiente del predictor e interpretar.
Ejercicio 2
Construir un modelo de regresión lineal múltiple para los puntajes de la prueba cognitiva de los niños usando el puntaje de la madre y la variable indicadora de si la madre se graduó o no de la secundaria como predictores. Obtener los intervalos al 97% de confianza para los coeficientes de los predictores del modelo e interpretar.
Ejercicio 3
En el modelo anterior, incluir la interacción entre los predictores y estimar el efecto marginal del puntaje de la madre sobre las categorías de la variable indicadora. Intrepretar los efectos marginales.