22 Análisis multinivel
En el modelo de regresión lineal se asume que los términos de error son independientes e idénticamente distribuídos. En la práctica, este supuesto de independencia implica que no existe asociación entre las fuentes de variabilidad no consideradas en el modelo de las respuestas inviduales de la muestra. Por ejemplo, digamos que queremos estudiar el efecto de un nuevo suplemento alimenticio en los niveles de hemoglobina de un grupo de niños. Cada niño es asignado aleatoriamente al grupo de control o al de tratamiento. Bajo el modelo de regresión lineal, el supuesto de independencia implica que para cualquier par de niños en la muestra no existe relación entre los otros factores que podrían estar influyendo en sus niveles de hemoglobina, luego de haber tomado en cuenta el efecto del tratamiento. Sin embargo, es posible también cambiar el diseño de muestreo, y en vez de que asignemos a los niños al grupo de control o tratamiento, asignamos los distritos de residencia de los niños a estos grupos, y luego en cada distrito escogemos a los niños para el estudio. De esta manera, los niños de un distrito en particular estarán dentro del mismo grupo de control o tratamiento. A este diseño se le llama muestreo por conglomerados. En este caso, es muy probable que las observaciones de los niveles de hemoglobina de los niños de un distrito estén más correlacionadas entre sí que entre los niveles de los niños de otros distritos. Por lo tanto, las observaciones de los niños comparten una fuente de variabilidad aparte del tratamiento al que han sido asignados, el efecto del distrito de residencia. Entonces, bajo un modelo de regresión lineal, con esta muestra podría ser inadecuado asumir que los errores sean independientes.
Los datos provenientes de un muestreo similar al descrito anteriormente para los distritos y niños tienen lo que se conoce como una estructura o diseño anidado. En un diseño anidado, se asume que los individuos pertecen a solo uno de los grupos o conglomerados. Por ejemplo, los niños residen (la mayor parte del tiempo) en solo uno de los distritos. Al nivel del cual se recogen las observaciones se le conoce como el primer nivel del diseño. En el ejemplo, el primer nivel lo constituyen los niños. Los distritos constituyen el segundo nivel del diseño. Técnicamente, el diseño puede tener más de dos niveles. Por ejemplo, la provincia puede constituir un tercer nivel, ya que un distrito pertenece solo a una provincia. En este capítulo solo trabajaremos con diseños anidados de dos niveles. Para analizar estos tipos de datos se usa el análisis multinivel, el cual consiste en usar un modelos de regresión multinivel que considere el efecto del agrupamiento de los datos. A estos modelos también se les conoce como modelos lineales jerárquicos o modelos lineales de efectos mixtos. No considerar el efecto del agrupamiento de los datos puede causar, entre otras cosas, una alta tasa de error de tipo I en los parámetros del modelo de regresión. Es decir, la probabilidad de erróneamente encontrar que un predictor tiene un efecto significativo en la respuesta podría ser más alta de lo esperado.
En este capítulo se hará una introducción al uso de R para el análisis multinivel. Como se mencionó, solo se abordarán diseños de dos niveles, es decir, inviduos agrupados en un solo nivel de conglomerados. El principal paquete en R para este tipo de análisis es el paquete lme4 (Bates et al. 2015). Veremos también otros paquetes con funcionalidad que permitan imprimir y visualizar los resultados de lme4 bajo el enfoque tidy.
22.1 Estrés en hospitales
Usarémos el archivo nurses.csv, que contiene los datos de una simulación de un experimento aleatorizado por conglomerados. En este supuesto estudio, se quiere analizar el efecto de un programa de entrenamiento para lidiar con el estrés en las enfermeras y los enfermeros de los pabellones de 25 hospitales. En cada hospital, se seleccionaron 4 pabellones y cada uno fue asignado aleatoriamente al grupo control (no se impartió el programa) o al de tratamiento (se impartió el programa). Una vez finalizado el programa, se escogieron aleatoriamente 10 enfermeras o enfermeros para una evaluación que mide el estrés relacionado con su trabajo. Este conjunto de datos fue presentado en Hox, Moerbeek, y Schoot (2017) y se puede descargar libremente en [https://multilevel-analysis.sites.uu.nl/datasets/]. El archivo nurses.csv es productor de haber transformado el archivo de datos original a formato CSV y de haber eliminado algunas columnas innecesarias para el propósito este capítulo.
Carguemos el paquete tidyverse y leamos el archivo:
nurses <- read_csv("data/nurses.csv")Podemos usar el comando View(fev) para dar un vistazo a la data:
View(nurses)En el conjunto de datos encontramos los datos para el identificador del hospital (hospital), el identificador del pabellón en cada hospital (ward), el identificador general del pabellón (wardid = hospital + ward), el identificador de la enfermera o el enfermero (nurse), la edad (age), el sexo (gender; 0: Hombre, 1: Mujer) y los años de experiencia (experien) de cada uno, el puntaje de estrés de la evaluación (stress), el tipo de pabellón (wardtype; 0: Cuidados generales, 1: Cuidados especiales), el tamaño del hospital (hospsize; 0: Pequeño, 1: Mediano, 2: Grande), y el grupo experimental (expcon; 0: Control, 1: Tratamiento).
Lo primero que podemos explorar de este conjunto de datos es la diferencia entre los puntajes de estrés entre los grupos de control y de tratamiento. Primero, transformemos las variables indicadoras en factores:
Grafiquemos el promedio para cada uno de los grupos:
nurses %>%
group_by(expcon) %>%
summarise(
stress_mean = mean(stress), stress_sd = sd(stress), .groups = "drop"
) %>%
ggplot(aes(x = expcon, y = stress_mean, color = expcon, group = expcon)) +
geom_pointrange(
aes(ymin = stress_mean - stress_sd, ymax = stress_mean + stress_sd)
)
Vemos que, en general, el personal que recibió el programa de entrenamiento tuvo un puntaje promedio de estrés menor que los que no recibieron el programa. Ahora, veamos los puntajes promedio por separado para cada hospital. Tomemos por ejemplos los primeros seis hospitales:
nurses %>%
filter(hospital %in% 1:6) %>%
group_by(hospital, expcon) %>%
summarise(
stress_mean = mean(stress), stress_sd = sd(stress), .groups = "drop"
) %>%
ggplot(aes(x = expcon, y = stress_mean, color = expcon, group = expcon)) +
geom_pointrange(
aes(ymin = stress_mean - stress_sd, ymax = stress_mean + stress_sd)
) +
facet_wrap(~hospital)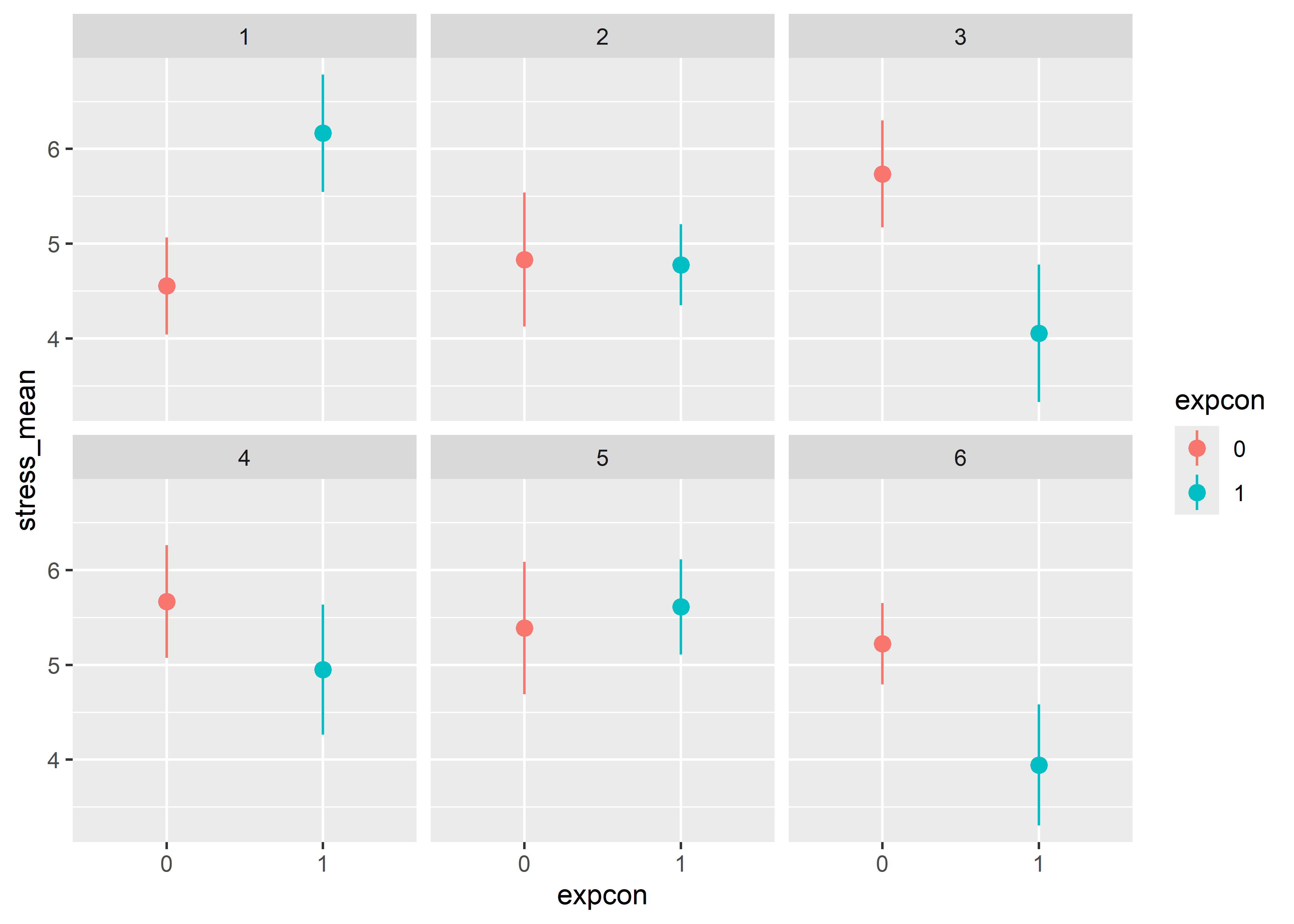
Podemos observar que la diferencia entre los puntajes de estrés de los grupos experimentales varía según el hospital. En hospital 1, por ejemplo, los grupos tienen un comportamiento contrario al general, ya que el grupo que sí recibió el programa de entrenamiento tuvo un puntaje promedio mayor al que no recibió. Además, en los grupos 2 y 5 pareciera no haber mucha diferencia. Entonces, vemos que en cada hospital ha sido diferente el impacto que ha tenido el tratamiento en el manejo del estrés.
Analicemos ahora los puntajes de estrés dentro de cada pabellón en de cada hospital. Veamos para los primeros seis hospitales:
nurses %>%
filter(hospital %in% 1:6) %>%
group_by(hospital, ward, expcon) %>%
summarise(
stress_mean = mean(stress), stress_sd = sd(stress), .groups = "drop"
) %>%
ggplot(aes(x = ward, y = stress_mean, color = expcon, group = expcon)) +
geom_pointrange(
aes(ymin = stress_mean - stress_sd, ymax = stress_mean + stress_sd)
) +
facet_wrap(~hospital)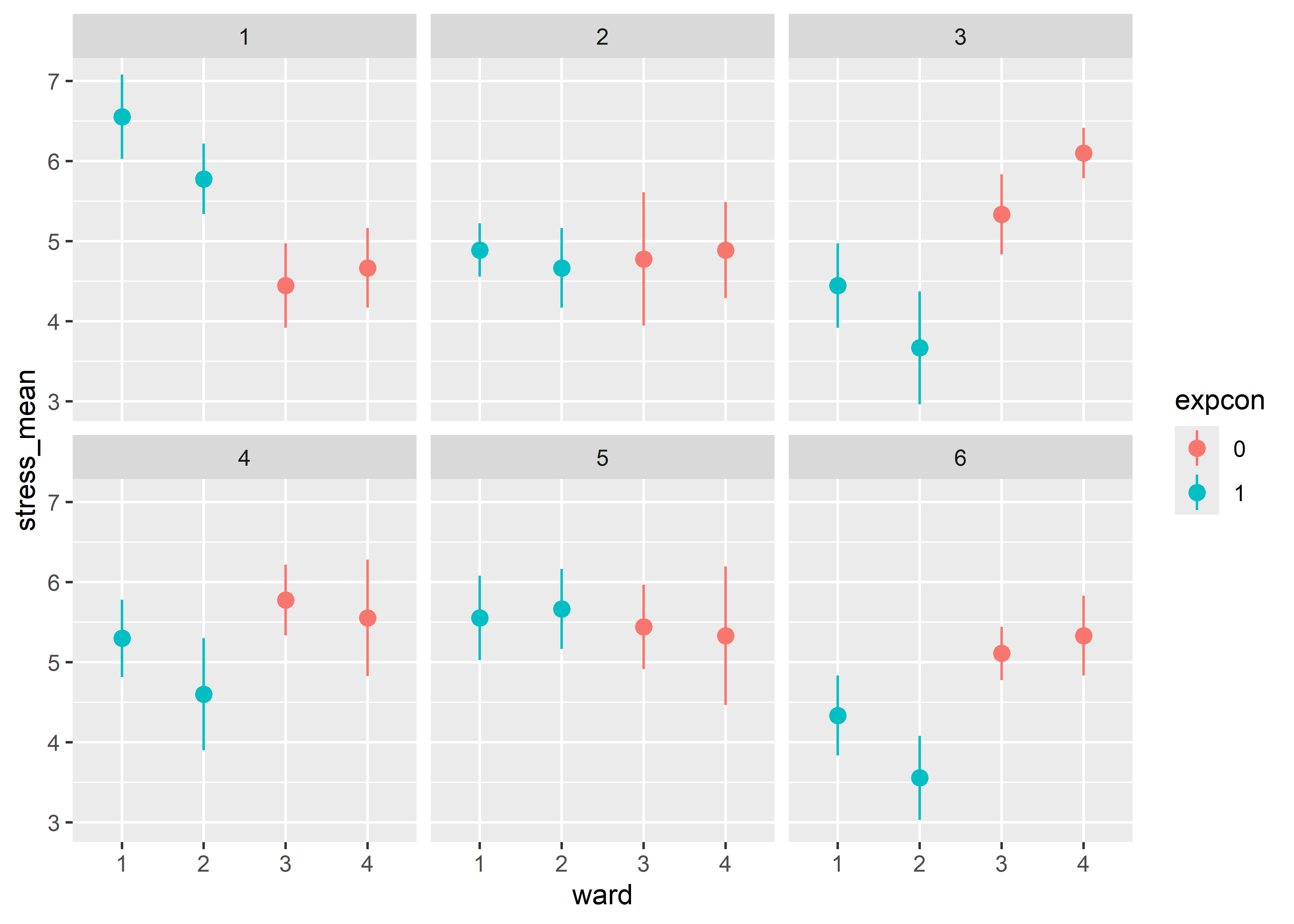
Observamos que incluso dentro de los mismos hospitales y grupos experimentales existen diferencias entre las puntuaciones de los pabellones. Por ejemplo, en el hospital 6, vemos que si bien los pabellones 1 y 2 que recibieron el programa de entrenamiento obtuvieron puntajes menores que los que no recibieron, el pabellón 2 obtuvo un menor puntaje en promedio que el pabellón 1. De esta manera podemos darnos cuenta la importancia de considerar la estructura de los datos a la hora de realizar el análisis de estos. Si no se considerara la estructura jerárquica de los datos, podemos generalizar erróneamente el efecto positivo del tratamiento a todos los pabellones. Más aún, si ajustamos un modelo de regresión lineal sin estructura jerárquica estaríamos omitiendo el importante efecto que tienen los grupos anidados (hospitales y pabellones) en la variabilidad de los puntajes de estrés.
En la siguiente sección veremos cómo ajustar modelos que consideran la estructura jerarquica o multinivel de este conjunto de datos usando el paquete lme4 de R.
22.2 Interceptos aleatorios
Asumiremos que los datos tienen solo dos niveles. El primero son los enfermeros o enfermeras y el segundo es el hospital-pabellón al que pertenecen. Es decir, combinaremos los identificadores del hospital y del pabellón. Este identificador ya se encuentra en el conjunto de datos para la variable wardid. Primero, construiremos un modelo con interceptos aleatorios para cada uno de estos pabellones únicamente identificados. En R, la función lmer() del paquete lme4 nos permite ajustar modelos con efectos aleatorios y mixtos (aleatorios y fijos).
Cargemos el paquete lme4:
El uso de esta función es similar al de la función lm() para ajustar modelos de regresión lineal:
lmer(formula, data, ...)La diferencia está en la fórmula. Para especificar sobre qué terminos del modelo se van a estimar los efectos aleatorios por grupo usamos una barra horizonatal (|). En el lado izquierdo de la barra se ponen los términos y al lado derecho la variable que define los grupos o factor de agrupación.
Si queremos interceptos aleatorios para cada pabellón (wardid) entonces incluirémos en la fórmula el término 1|wardid. Se usa un paréntesis para separar este término de los otros componentes del modelo:
model_ri <- lmer(stress ~ 1 + (1 | wardid), data = nurses) Podemos usar la función summary() para ver un resumen del modelo ajustado:
summary(model_ri)Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ 1 + (1 | wardid)
Data: nurses
REML criterion at convergence: 1952.4
Scaled residuals:
Min 1Q Median 3Q Max
-2.94699 -0.67691 -0.00005 0.69678 3.12110
Random effects:
Groups Name Variance Std.Dev.
wardid (Intercept) 0.6576 0.8109
Residual 0.3013 0.5489
Number of obs: 1000, groups: wardid, 100
Fixed effects:
Estimate Std. Error t value
(Intercept) 5.00065 0.08295 60.28Este resumen contiene las siguientes secciones:
-
Formula: La fórmula del modelo. -
Data: El conjunto de datos usado. -
REML criterion at convergence: La devianza del modelo ajustado usando el algoritmo de máxima verosimilitud restringida (REML, por sus siglas en inglés). También es posible ajustar el modelo usando el algoritmo de máxima verosimilitud (MLE, por sus siglas en inglés). -
Scaled residuals: Estadísticas descriptivas de los residuales escalados. -
Random effects: Tabla con la estimación de la varianza de los efectos aleatorios y su desviación estándar en cada grupo. La columnaGroupincluye los grupos,Nameel término para el cual se han estimado los efectos aleatorios (en este caso para el intercepto),Variancela varianza estimada, yStd.Dev.la desviación estándar de las varianzas estimadas. Además en la parte inferior se incluye el número de observaciones total (Number of obs) y el número de grupos (groups). -
Fixed effects: Tabla con los efectos fijos estimados.Estimatecontiene las estimaciones puntuales,Std. Errorsus errores estándar yt valuelas estadísticas
De estos resultados podemos estimar que la varianza de los puntajes de estrés entre los pabellones es de 0.66 y que el promedio general de los puntajes es de 5. Vemos que la varianza entre los grupos es mayor que la varianza residual, lo que indica que gran parte de la varibilidad de la respuesta está explicada por los grupos. Un indicador de qué tan importante son los grupos para explicar la varibilidad de la respuesta es el coeficiente de correlación interclase (ICC, por sus siglas en inglés). Este se puede calcular con la función icc() del paquete performance:
library(performance)
icc(model_ri)# Intraclass Correlation Coefficient
Adjusted ICC: 0.686
Unadjusted ICC: 0.686El ICC es la proporción de la varianza total que es explicada por los grupos. El ICC ajustado (Adjusted ICC) considera para el cálculo solo la varianza de los efectos aleatorios. De los resultados del modelo model_ri, el ICC podría calcularse como la división entre la varianza estimada de los efectos aleatorios y la suma entre esta varianza y la varianza residual: 0.6575997 / (0.6575997 + 0.3012716) = 0.685806.
El ICC no ajustado (Unadjusted ICC), por otro lado, considera también en el cálculo la varianza explicada por los efectos fijos incluidos en el modelo (aparte del intercepto general).
Para pasar los resultados del ajuste con la función lmer() a formato tidy (tabular) podemos usar la función tidy() del paquete broom.mixed. Este paquete es una extensión del paquete broom que se vio en capítulos anteriores:
library(broom.mixed)
tidy(model_ri)# A tibble: 3 × 6
effect group term estimate std.error statistic
<chr> <chr> <chr> <dbl> <dbl> <dbl>
1 fixed <NA> (Intercept) 5.00 0.0830 60.3
2 ran_pars wardid sd__(Intercept) 0.811 NA NA
3 ran_pars Residual sd__Observation 0.549 NA NA Por defecto, la función tidy() nos desvuele un data frame con las siguientes columnas:
-
effect: El tipo de efecto estimado.fixedhace referencia a los efectos fijos, mientras queran_parsa los efectos aleatorios. -
group: El group o nivel para el cual fueron estimados los efectos aleatorios. -
term: El término para el cual fueron estimados los efectos fijos o aleatorios. -
estimate: La estimación puntal del efecto fijo, o la estimación de la varianza de los efectos aleatorios. -
std.error: El error estándar de los parámetros ajustados (efectos fijos). -
statistic: La estadística de prueba de los efectos fijos.
Podemos obtener los efectos aleatorios usando la función ranef() del paquete lme4. Esta función devuelve una lista de data frames, uno para cada factor de agrupación que se haya usado en el modelo. Si transformamos esta lista a data frame usando as.data.frame() o as_tibble(), obtenemos un solo data frame con los efectos aleatorios de todos los grupos:
model_ri_ranef <- ranef(model_ri)
model_ri_ranef_df <- as_tibble(model_ri_ranef)
model_ri_ranef_df %>%
slice_head(n = 10)# A tibble: 10 × 5
grpvar term grp condval condsd
<chr> <fct> <fct> <dbl> <dbl>
1 wardid (Intercept) 11 1.48 0.178
2 wardid (Intercept) 12 0.739 0.178
3 wardid (Intercept) 13 -0.529 0.178
4 wardid (Intercept) 14 -0.318 0.178
5 wardid (Intercept) 21 -0.106 0.178
6 wardid (Intercept) 22 -0.318 0.178
7 wardid (Intercept) 23 -0.212 0.178
8 wardid (Intercept) 24 -0.106 0.178
9 wardid (Intercept) 31 -0.529 0.178
10 wardid (Intercept) 32 -1.27 0.178grpvar indica el factor de agrupación, term el término para el cual se hallaron los efectos aleatorios, grp el grupo, condval el efecto aleatorio estimado, y condsd las desviación estándar del efecto aleatorio. El prefijo cond hace referencia a que estas estimaciones se han hecho condicionales a los otros parámetros del modelo y a la data.
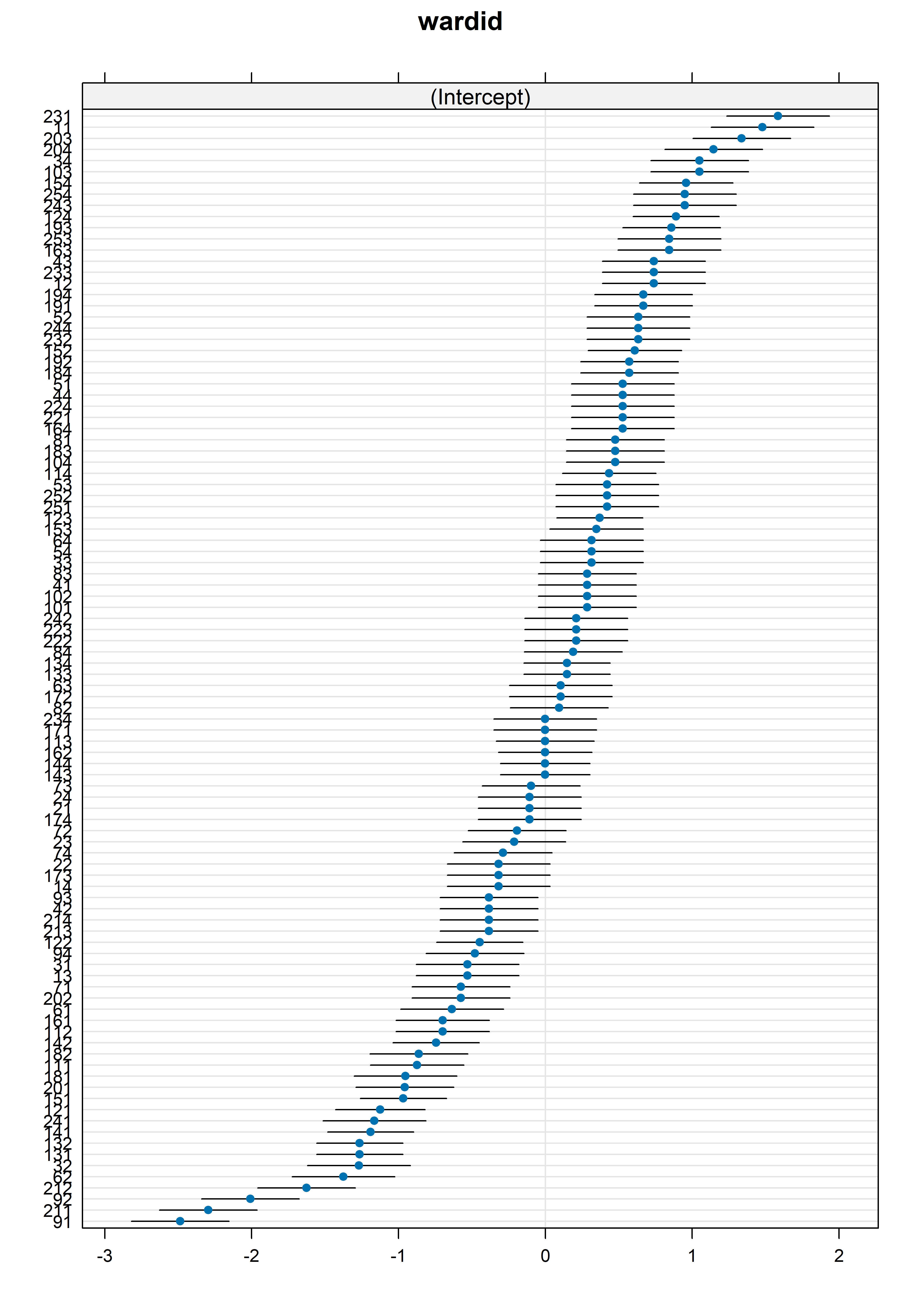
La función dotplot() del paquete lattice puede usarse sobre la salida de ranef() para generar una lista de dot plots o caterpillar plots por factor de agrupación:
Este gráfico muestra los efectos aleatorios estimados y sus intervalos al 95% de confianza para cada grupo. Si quisiéramos construir este gráfico usando ggplot2, podemos hacerlo fácilmente con los efectos aleatorios en formato tidy como se encuentran en model_ri_ranef_df:
model_ri_ranef_df %>%
ggplot(aes(x = grp, y = condval)) +
geom_pointrange(
aes(ymin = condval - 1.96 * condsd, ymax = condval + 1.96 * condsd)
) +
coord_flip()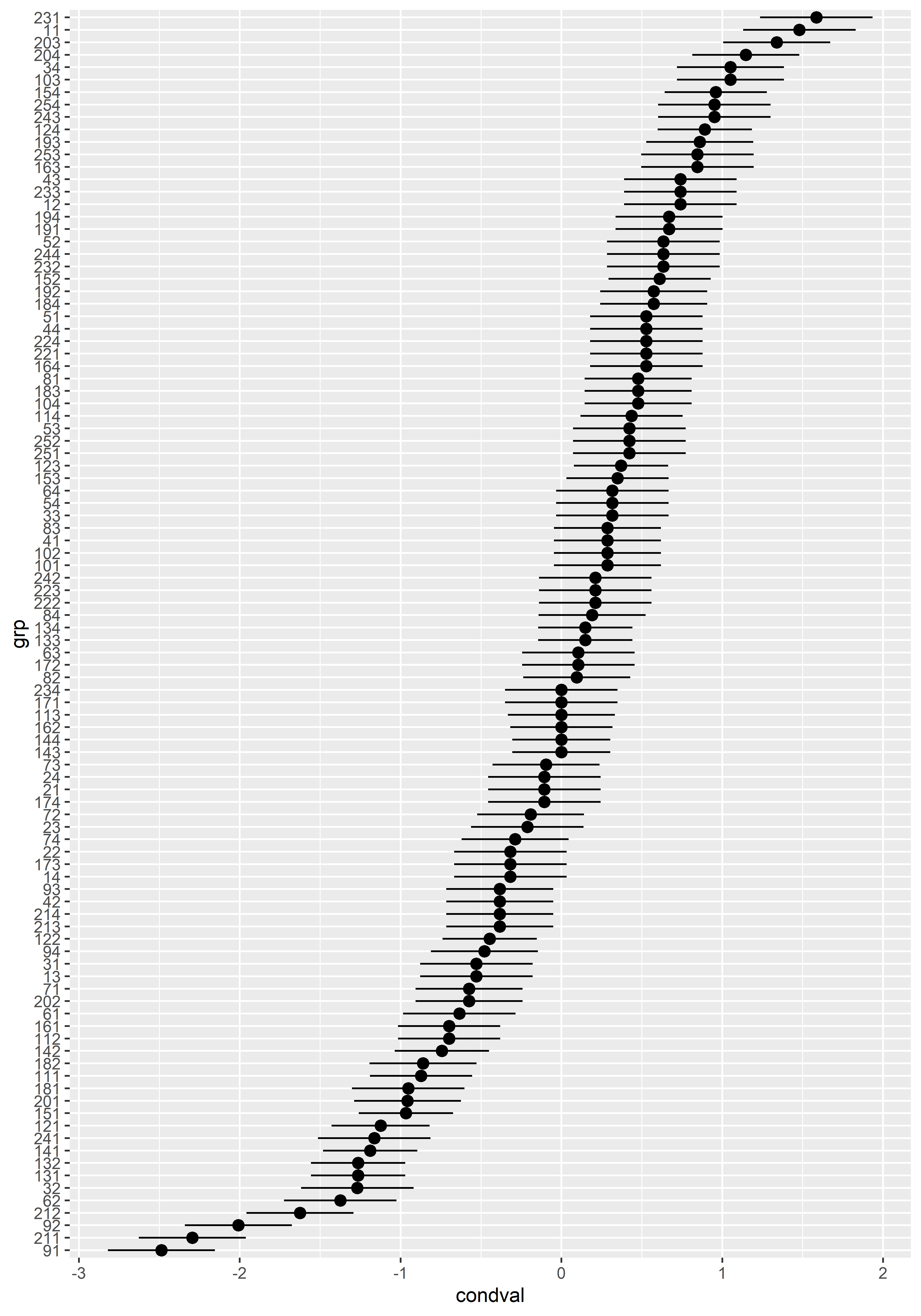
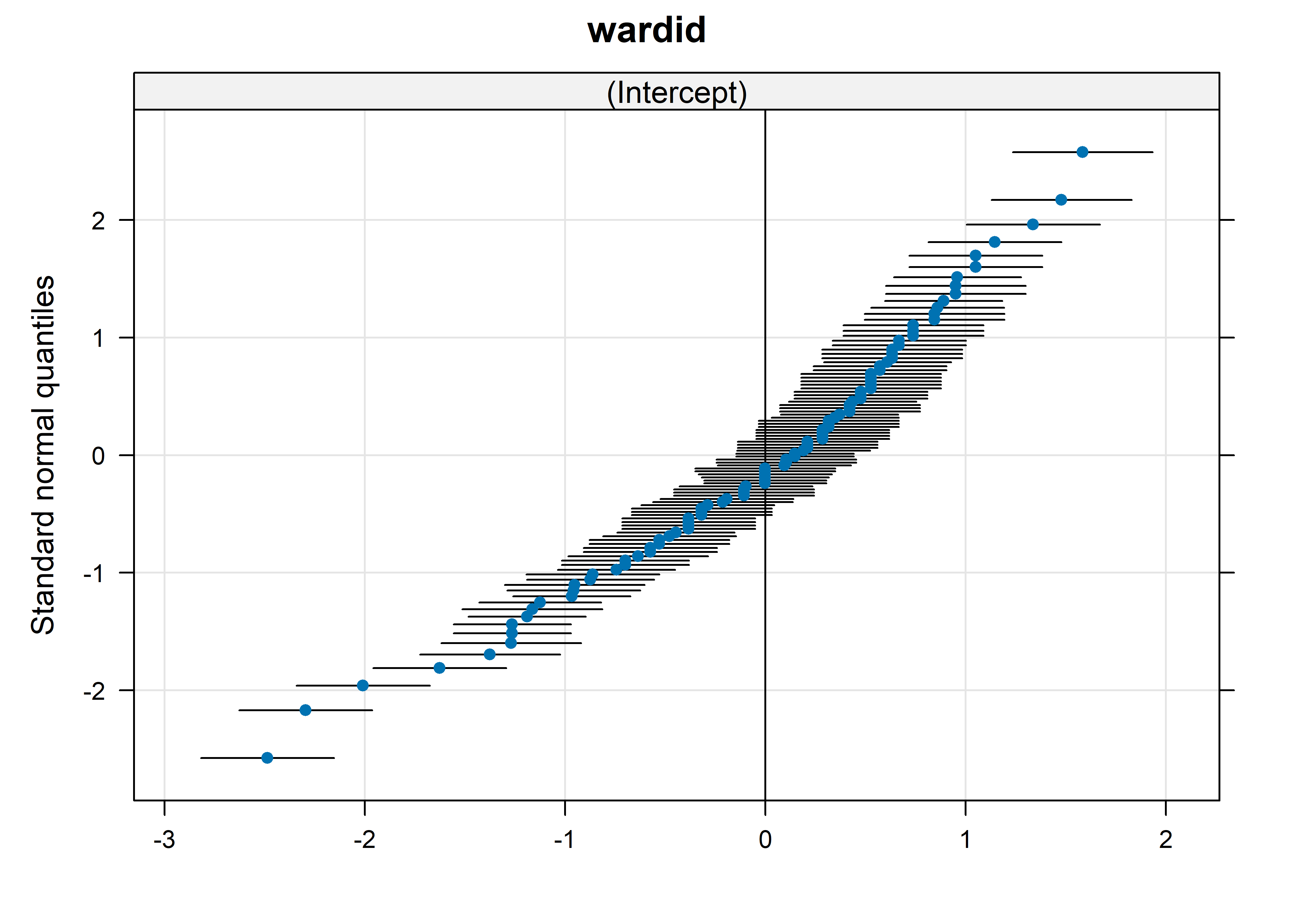
También podemos usar la función qqmath() del paquete lattice para generar una lista de QQ-plots para cada uno de los factores de agrupación:
Este gráfico sirve para verificar si los efectos aleatorios estimados se ajustan a una distribución normal.
Por último, podemos obtener los valores ajustados para cada observación en una tabla con la función augment() del paquete broom.mixed:
model_ri_fit <- augment(model_ri)
model_ri_fit %>%
slice_head(n = 10)# A tibble: 10 × 13
stress wardid .fitted .resid .hat .cooksd .fixed .mu .offset .sqrtXwt
<dbl> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 7 11 6.48 0.520 0.106 0.119 5.00 6.48 0 1
2 7 11 6.48 0.520 0.106 0.119 5.00 6.48 0 1
3 7 11 6.48 0.520 0.106 0.119 5.00 6.48 0 1
4 6 11 6.48 -0.480 0.106 0.101 5.00 6.48 0 1
5 6 11 6.48 -0.480 0.106 0.101 5.00 6.48 0 1
6 6 11 6.48 -0.480 0.106 0.101 5.00 6.48 0 1
7 6 11 6.48 -0.480 0.106 0.101 5.00 6.48 0 1
8 7 11 6.48 0.520 0.106 0.119 5.00 6.48 0 1
9 7 11 6.48 0.520 0.106 0.119 5.00 6.48 0 1
10 6 12 5.74 0.260 0.106 0.0297 5.00 5.74 0 1
# ℹ 3 more variables: .sqrtrwt <dbl>, .weights <dbl>, .wtres <dbl>En la columna .fitted tenemos los valores ajustados considerendo los efectos fijos, mientras que en la columna .fixed los valores ajustados sin considerar los efectos fijos. En este modelo, la columna .fixed contiene el valor del intercepto general que podemos ver en el resumen del modelo (5.000813). Los valores de la columna .fitted son, en este caso, la suma del intercepto general del modelo y el efecto aleatorio para cada observación. Por ejemplo, para la primera observación del pabellón 11, el efecto aleatorio en model_ri_ranef_df bajo la columna condval es 1.4795847. Si le sumamos este valor al intercepto general obtenemos el valor ajustado o media condicional, que es igual al valor de la primera observación en la columna .fitted en model_ri_fit:
model_ri_fit$.fixed[1] + model_ri_ranef_df$condval[1] 1
6.480238 La función augment() también devuelve otras columnas, como .resid que contienen los residuales. El resto de columnas son medidas basadas en los residuales y otros componentes del modelo que para esta introducción no son muy relevantes.
Ahora, agreguemos el efecto fijo de un predictor de primer nivel al modelo anterior. De esta manera, obtendremos un modelo de efectos mixtos; es decir, con efectos fijos y aleatorios. Un predictor de primer nivel estaría asociado a las enfermeras o enfermeros. Por ejemplo, incluyamos el efecto fijo de los años de experiencia (experien):
Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ experien + (1 | wardid)
Data: nurses
REML criterion at convergence: 1898.1
Scaled residuals:
Min 1Q Median 3Q Max
-2.8446 -0.6774 -0.0076 0.6692 3.1786
Random effects:
Groups Name Variance Std.Dev.
wardid (Intercept) 0.6557 0.8098
Residual 0.2810 0.5301
Number of obs: 1000, groups: wardid, 100
Fixed effects:
Estimate Std. Error t value
(Intercept) 5.408204 0.096663 55.949
experien -0.023925 0.002937 -8.146
Correlation of Fixed Effects:
(Intr)
experien -0.517Vemos que en la tabla de Fixed effects se han añadido la estimación del coeficiente de los años de experiencia en el modelo. Esta estimación nos dice que la media del puntaje de estrés disminuye en 0.02 por un aumento de un año de experiencia, manteniento otras condiciones constantes. Además, se imprime una nueva sección Correlation of Fixed Effects. Esta contiene la matriz de correlación de los efectos fijos; en este caso, del intercepto general y los años de experiencia. Generalmente, no se presta mucha atención a esta sección ya que es fácil de malinterpretar.
Si calculamos el ICC para este modelo, obtenemos estimaciones diferentes para el ICC ajustado y el no ajustado:
icc(model_ri_simple)# Intraclass Correlation Coefficient
Adjusted ICC: 0.700
Unadjusted ICC: 0.685Esto se debe, como se explicó anteriormente, a que el ICC no ajustado considera también la varianza de los efectos fijos diferentes al del intercepto general.
Los interceptos aleatorios definen diferentes interceptos para las líneas de regresión de la asociación del estrés y los años de experiencia en cada grupo. Además, estas líneas tendrían pendientes iguales ya que el efecto fijo de los años de experiencia es el mismo para todos los grupos. Para visualizar estas líneas de regresión paralelas, necesitamos los valores ajustados del modelo. Podemos obtenerlos con la función augment():
model_ri_simple_fit <- augment(model_ri_simple)model_ri_simple_fit %>%
slice_head(n = 10)# A tibble: 10 × 14
stress experien wardid .fitted .resid .hat .cooksd .fixed .mu .offset
<dbl> <dbl> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 7 11 11 6.62 0.379 0.107 0.0344 5.15 6.62 0
2 7 20 11 6.41 0.594 0.106 0.0838 4.93 6.41 0
3 7 7 11 6.72 0.283 0.109 0.0196 5.24 6.72 0
4 6 25 11 6.29 -0.286 0.108 0.0198 4.81 6.29 0
5 6 22 11 6.36 -0.358 0.107 0.0305 4.88 6.36 0
6 6 22 11 6.36 -0.358 0.107 0.0305 4.88 6.36 0
7 6 13 11 6.57 -0.573 0.107 0.0779 5.10 6.57 0
8 7 13 11 6.57 0.427 0.107 0.0433 5.10 6.57 0
9 7 17 11 6.48 0.523 0.106 0.0646 5.00 6.48 0
10 6 21 12 5.72 0.280 0.106 0.0185 4.91 5.72 0
# ℹ 4 more variables: .sqrtXwt <dbl>, .sqrtrwt <dbl>, .weights <dbl>,
# .wtres <dbl>Ahora, podemos construir el gráfico con las líneas paralelas:
model_ri_simple_fit %>%
ggplot(aes(x = experien)) +
geom_point(aes(y = stress)) +
geom_line(aes(y = .fitted, group = wardid)) +
geom_line(aes(y = .fixed), color = "red", linewidth = 1)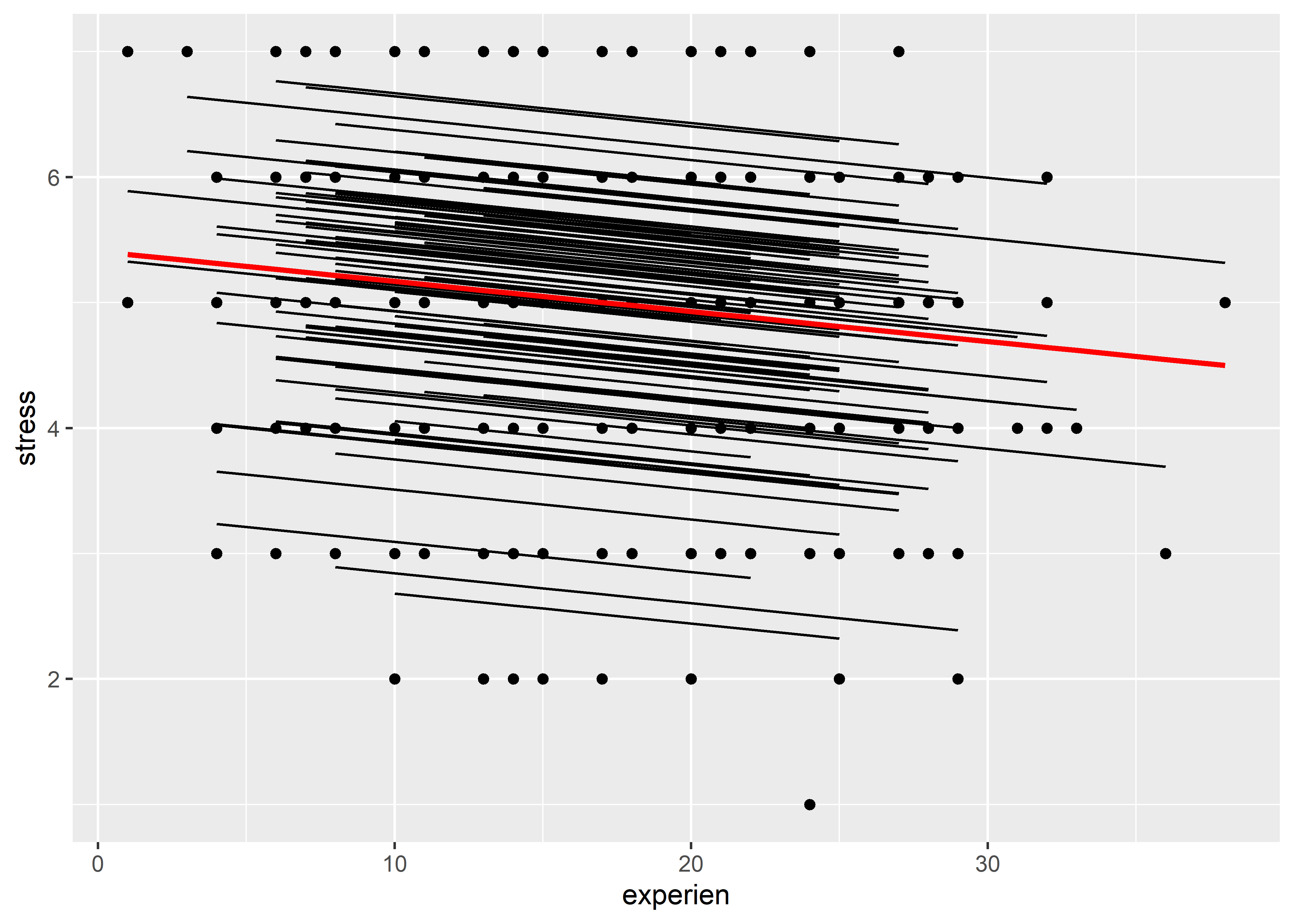
Aquí hemos incluido también la línea de regresión general de color rojo. Las líneas de color negro son las líneas de regresión de cada grupo. Vemos que se si las extendemos hasta el eje de strees tienen diferentes interceptos, pero son paralelas entre sí ya que tienen la misma pendiente (mismo coeficiente estimado para experien).
Para extraer los coeficientes del modelo podemos usar la función coef(). Esta función devuelve una lista de data frames por cada factor de agrupación. En este caso, solo tenemos al factor de agrupación wardid:
coef(model_ri_simple)$wardid[1:10, ] (Intercept) experien
11 6.884015 -0.02392459
12 6.222793 -0.02392459
13 4.876485 -0.02392459
14 5.131742 -0.02392459
21 5.354012 -0.02392459
22 5.073380 -0.02392459
23 5.169291 -0.02392459
24 5.348937 -0.02392459
31 4.932309 -0.02392459
32 4.118839 -0.02392459Vemos que los coeficientes de experien (pendientes de la línea de regresión estimada) son iguales. Para efectos didácticos, podemos pintar las líneas en el gráfico anterior según el valor de su pendiente. En este caso, sería un solo color ya que las pendientes son iguales. Para poder hacer este gráfico tenemos que primero pasar los nombres de las filas del data frame, que corresponden a los valores de wardid, a una columna con nombre wardid. Eso lo podemos hacer con la función rownames_to_column() del paquete tibble (este paquete se carga con tidyverse):
model_ri_simple_coef <- coef(model_ri_simple)$wardid %>%
as_tibble() |>
rownames_to_column(var = "wardid")model_ri_simple_coef %>%
slice_head(n = 10)# A tibble: 10 × 3
wardid `(Intercept)` experien
<chr> <dbl> <dbl>
1 1 6.88 -0.0239
2 2 6.22 -0.0239
3 3 4.88 -0.0239
4 4 5.13 -0.0239
5 5 5.35 -0.0239
6 6 5.07 -0.0239
7 7 5.17 -0.0239
8 8 5.35 -0.0239
9 9 4.93 -0.0239
10 10 4.12 -0.0239Luego, podemos usar la función inner_join() para juntar model_ri_simple_fit y model_ri_simple_coef por wardid:
model_ri_simple_coef_fit <- model_ri_simple_coef %>%
rename(intercept = `(Intercept)`, slope = experien) %>%
inner_join(model_ri_simple_fit, by = "wardid")model_ri_simple_coef_fit %>%
slice_head(n = 10)# A tibble: 10 × 16
wardid intercept slope stress experien .fitted .resid .hat .cooksd .fixed
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 11 5.77 -0.0239 7 11 6.62 0.379 0.107 0.0344 5.15
2 11 5.77 -0.0239 7 20 6.41 0.594 0.106 0.0838 4.93
3 11 5.77 -0.0239 7 7 6.72 0.283 0.109 0.0196 5.24
4 11 5.77 -0.0239 6 25 6.29 -0.286 0.108 0.0198 4.81
5 11 5.77 -0.0239 6 22 6.36 -0.358 0.107 0.0305 4.88
6 11 5.77 -0.0239 6 22 6.36 -0.358 0.107 0.0305 4.88
7 11 5.77 -0.0239 6 13 6.57 -0.573 0.107 0.0779 5.10
8 11 5.77 -0.0239 7 13 6.57 0.427 0.107 0.0433 5.10
9 11 5.77 -0.0239 7 17 6.48 0.523 0.106 0.0646 5.00
10 12 6.44 -0.0239 6 21 5.72 0.280 0.106 0.0185 4.91
# ℹ 6 more variables: .mu <dbl>, .offset <dbl>, .sqrtXwt <dbl>, .sqrtrwt <dbl>,
# .weights <dbl>, .wtres <dbl>En este último data frame, ya tenemos los interceptos (intercept) y las pendientes (slope) para cada observación. Como era de esperarse, las pendientes son iguales. Ahora podemos generar el gráfico:
model_ri_simple_coef_fit %>%
ggplot(aes(x = experien)) +
geom_point(aes(y = stress), size = 0.5) +
geom_line(aes(y = .fitted, group = wardid, color = slope)) +
geom_line(aes(y = .fixed), color = "red", linewidth = 1)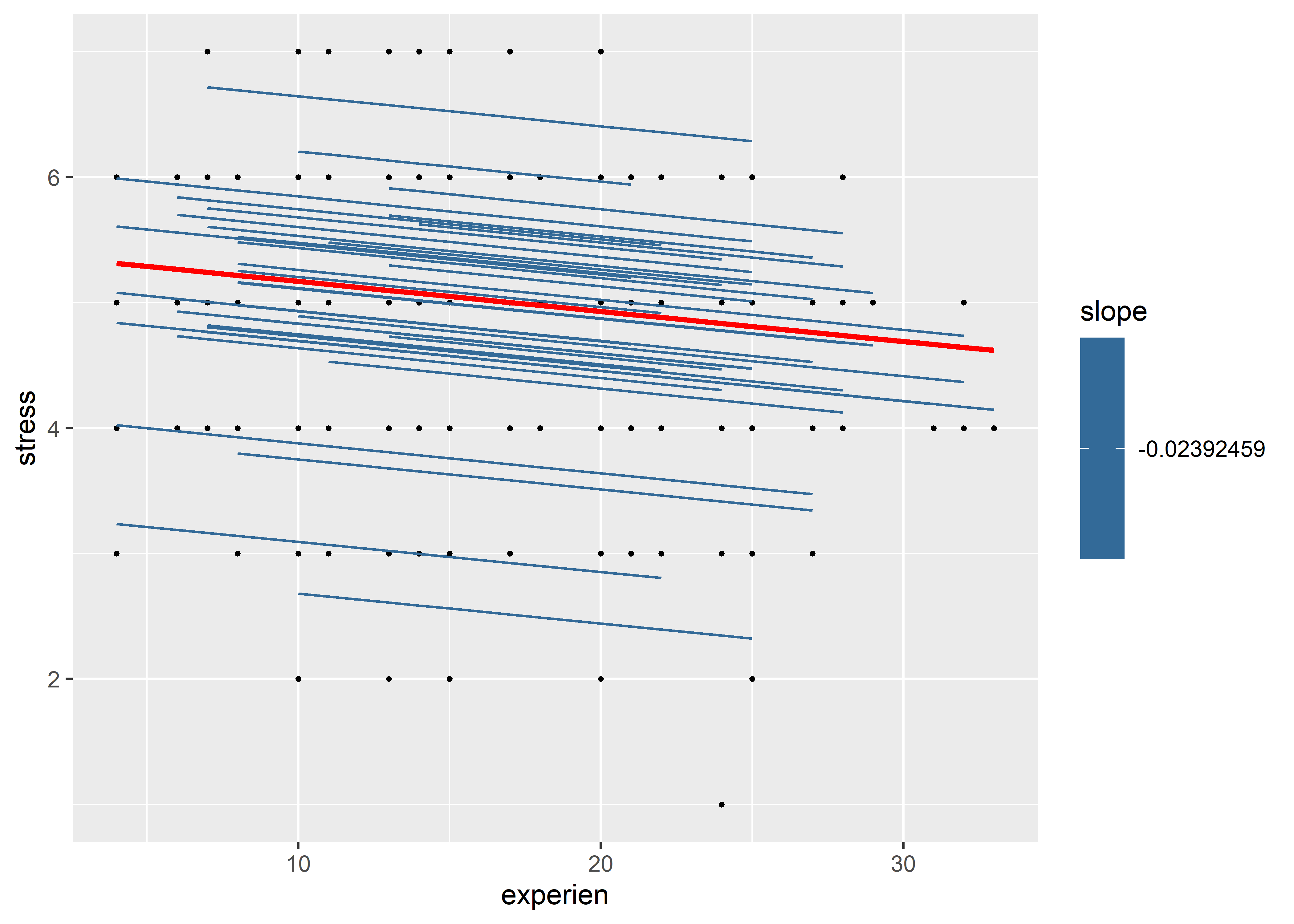
Este gráfico no dice mucho más que el anterior, pero en la siguiente sección veremos cómo ajustar por pendientes (coeficientes) aleatorias para que grupo tenga una pendiente diferente y podamos visualizarla las diferencias en este tipo de gráfico.
22.3 Interceptos y coeficientes aleatorios
En un modelo de coeficientes aleatorios se estima un efecto aleatorio para el coeficiente asociado a un predictor en cada grupo. Por ejemplo, si queremos estimar efectos aleatorios para el coeficiente de los años de experiencia usamos la siguiente fórmula en la función lmer():
model_rc <- lmer(stress ~ experien + (experien|wardid), data = nurses)Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge with max|grad| = 0.0202527 (tol = 0.002, component 1)summary(model_rc)Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ experien + (experien | wardid)
Data: nurses
REML criterion at convergence: 1897.6
Scaled residuals:
Min 1Q Median 3Q Max
-2.8447 -0.6820 -0.0057 0.6729 3.1916
Random effects:
Groups Name Variance Std.Dev. Corr
wardid (Intercept) 6.269e-01 0.791799
experien 5.261e-05 0.007253 0.09
Residual 2.790e-01 0.528201
Number of obs: 1000, groups: wardid, 100
Fixed effects:
Estimate Std. Error t value
(Intercept) 5.40457 0.09518 56.781
experien -0.02368 0.00303 -7.817
Correlation of Fixed Effects:
(Intr)
experien -0.493
optimizer (nloptwrap) convergence code: 0 (OK)
Model failed to converge with max|grad| = 0.0202527 (tol = 0.002, component 1)Vemos en la sección de Random effects que se ha agregado los efectos aleatorios para el coeficiente de los años de experiencia. Sin embargo, la varianza estimada de estos es bastante pequeña en comparación a las otras varianzas estimadas, lo que indica que no hay mucha variabilidad entre los efectos aleatorios de este coeficiente a través de los grupos. Además, en la columna Corr de esta sección, se ha añadido la correlación entre los efectos aleatorios del intercepto y el coeficiente de experien.
La función lmer() también nos devuelve un mensaje de advertencia diciendo que el modelo falló en converger. Los detalles del mensaje no son relevantes por ahora, pero lo que significa la no convergencia es que las estimaciones del modelo no alcanzaron un nivel mínimo de estabilidad. Esto es usual en modelos complejos como los que estamos viendo en este capítulo. La solución más común es probar con diferentes tipos de optimizadores. Los optimizadores son algoritmos que se encargan de encontrar las estimaciones óptimas según el criterio de ajuste (MLE o REML). En lme4, la función allFit() nos permite probar el ajuste de un modelo con todos los optimizadores disponibles:
allFit(model_rc)bobyqa : [OK]
Nelder_Mead : [OK]
nlminbwrap : [OK]
nloptwrap.NLOPT_LN_NELDERMEAD : boundary (singular) fit: see help('isSingular')[OK]
nloptwrap.NLOPT_LN_BOBYQA : Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge with max|grad| = 0.0202527 (tol = 0.002, component 1)[OK]original model:
stress ~ experien + (experien | wardid)
data: nurses
optimizers (5): bobyqa, Nelder_Mead, nlminbwrap, nloptwrap.NLOPT_LN_NELDERMEAD,nloptwrap.NLO...
differences in negative log-likelihoods:
max= 0.0753 ; std dev= 0.0337 No entraremos en detalle sobre cada uno de los optimizadores, pero aquellos que no produjeron mensajes de advertencia (en color rojo) son los que no tuvieron problemas en convergencia. Es decir, podríamos probar ajustando el modelo usando los optimizadores bobyqa, Nelder_Mead o nlminbwrap. Si quisieramos saber con cuál de estos optimizadores se obtiene una mejor convergencia, podemos pasar los resultados de allFit() en una tabla usando la función glance() del paquete broom.mixed:
model_rc_all_fit <- allFit(model_rc, verbose = FALSE)boundary (singular) fit: see help('isSingular')Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
Model failed to converge with max|grad| = 0.0202527 (tol = 0.002, component 1)glance(model_rc_all_fit)# A tibble: 5 × 9
optimizer nobs sigma logLik AIC BIC REMLcrit df.residual NLL_rel
<chr> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl>
1 bobyqa 1000 0.528 -949. 1910. 1939. 1898. 994 6.04e- 9
2 Nelder_Mead 1000 0.528 -949. 1910. 1939. 1898. 994 6.83e-10
3 nlminbwrap 1000 0.528 -949. 1910. 1939. 1898. 994 0
4 nloptwrap.NLOPT_… 1000 0.530 -949. 1910. 1939. 1898. 994 7.53e- 2
5 nloptwrap.NLOPT_… 1000 0.528 -949. 1910. 1939. 1898. 994 1.18e- 4En esta tabla, tenemos que fijarnos en la columna NLL_rel, que es la log-verosimilitud negativa con respecto al mejor ajuste. El mejor ajuste lo da el optimizador para el cual NLL_rel es igual a 0, que en este caso es nlminbwrap. Por lo tanto, reajustremos el modelo usando este optimizador:
model_rc <- lmer(
stress ~ experien + (experien|wardid), data = nurses,
control = lmerControl(optimizer = "nlminbwrap")
)
summary(model_rc)Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ experien + (experien | wardid)
Data: nurses
Control: lmerControl(optimizer = "nlminbwrap")
REML criterion at convergence: 1897.6
Scaled residuals:
Min 1Q Median 3Q Max
-2.8444 -0.6821 -0.0058 0.6729 3.1914
Random effects:
Groups Name Variance Std.Dev. Corr
wardid (Intercept) 6.250e-01 0.790591
experien 5.204e-05 0.007214 0.09
Residual 2.791e-01 0.528265
Number of obs: 1000, groups: wardid, 100
Fixed effects:
Estimate Std. Error t value
(Intercept) 5.404542 0.095084 56.840
experien -0.023681 0.003029 -7.818
Correlation of Fixed Effects:
(Intr)
experien -0.493Vemos que los resultados son muy similares a los obtenidos anteriormente, pero ahora ya no tenemos el problema de convergencia.
A pesar de no hay mucha variación entre los efectos aleatorios para el coeficiente de experien, por fines demostrativos graficaremos las líneas de regresión que se generan por la inclusión de estos coeficiente aleatorios. Estas líneas de regresión tendrán tanto interceptos como pendientes diferentes en cada grupo:
model_rc_fit <- augment(model_rc)
model_rc_coef <- rownames_to_column(
coef(model_rc)$wardid, var = "wardid"
)
model_rc_coef_fit <- model_rc_coef %>%
rename(intercept = `(Intercept)`, slope = experien) %>%
inner_join(model_rc_fit, by = "wardid")
model_rc_coef_fit %>%
ggplot(aes(x = experien)) +
geom_point(aes(y = stress), size = 0.5) +
geom_line(aes(y = .fitted, group = wardid, color = slope)) +
geom_line(aes(y = .fixed), color = "red", linewidth = 1)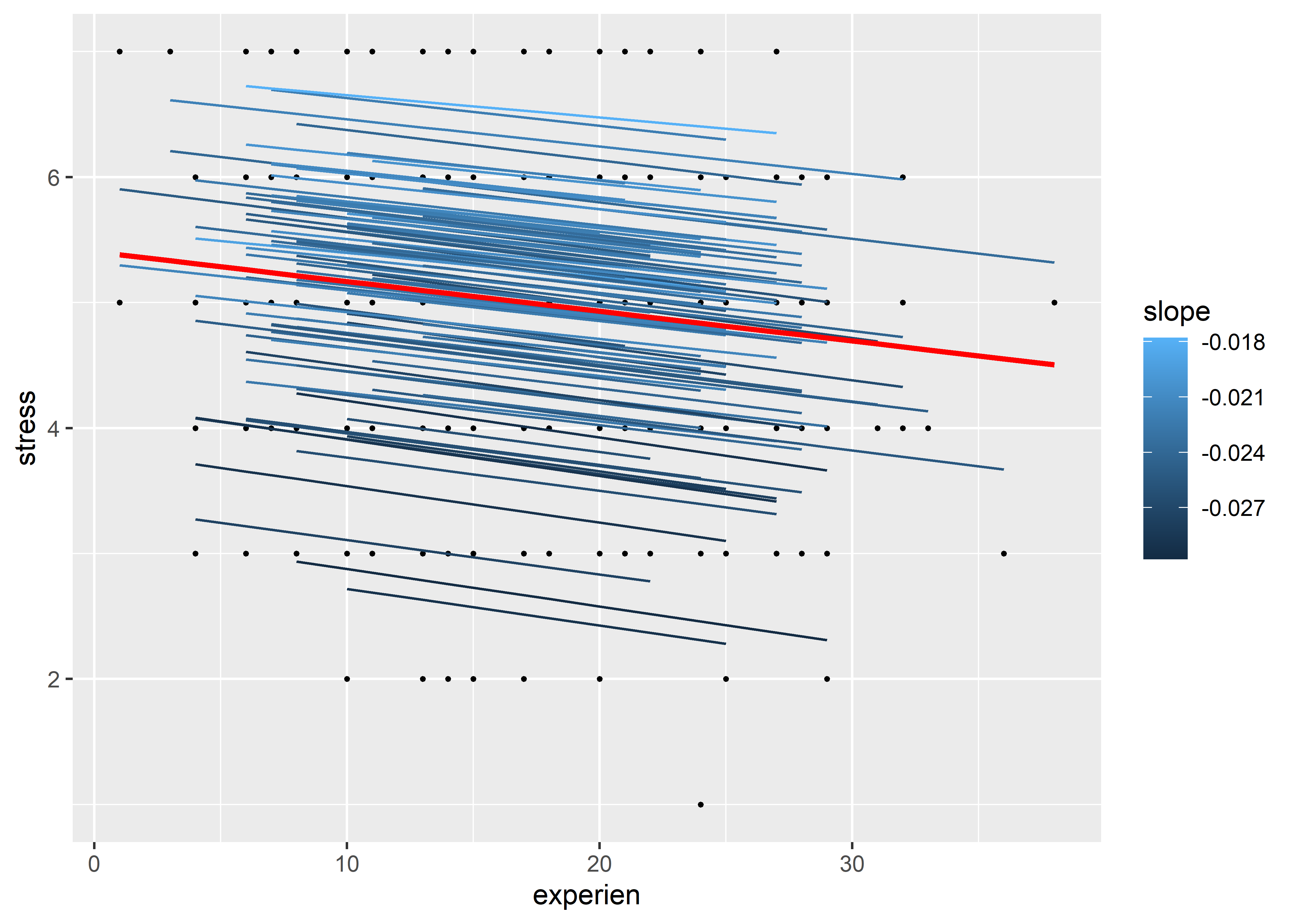
Podemos distinguir con algo de esfuerzo que no todas las líneas tienen pendientes iguales; sin embargo, la diferencia entre las pendientes son mínimas.
22.4 Interceptos fijos, coeficientes aleatorios
Si quisiéramos eliminar los interceptos aleatorios y solo quedarnos con los efectos aleatorios para el coeficiente de experien, añadimos un -1 antes de experien en el término de efectos aleatorios de la fórmula:
Linear mixed model fit by REML ['lmerMod']
Formula: stress ~ experien + (-1 + experien | wardid)
Data: nurses
REML criterion at convergence: 2101.3
Scaled residuals:
Min 1Q Median 3Q Max
-3.07249 -0.64443 -0.06056 0.71350 2.99431
Random effects:
Groups Name Variance Std.Dev.
wardid experien 0.001936 0.044
Residual 0.354059 0.595
Number of obs: 1000, groups: wardid, 100
Fixed effects:
Estimate Std. Error t value
(Intercept) 5.351507 0.058926 90.818
experien -0.020455 0.005511 -3.711
Correlation of Fixed Effects:
(Intr)
experien -0.570Este modelo produce líneas de regresión con interceptos iguales pero pendientes diferentes:
model_firc_fit <- augment(model_firc)
model_firc_coef <- rownames_to_column(
coef(model_firc)$wardid, var = "wardid"
)
model_firc_coef_fit <- model_firc_coef %>%
rename(intercept = `(Intercept)`, slope = experien) %>%
inner_join(model_firc_fit, by = "wardid")
model_firc_coef_fit %>%
ggplot(aes(x = experien)) +
geom_point(aes(y = stress), size = 0.5) +
geom_line(aes(y = .fitted, group = wardid, color = slope)) +
geom_line(aes(y = .fixed), color = "red", linewidth = 1)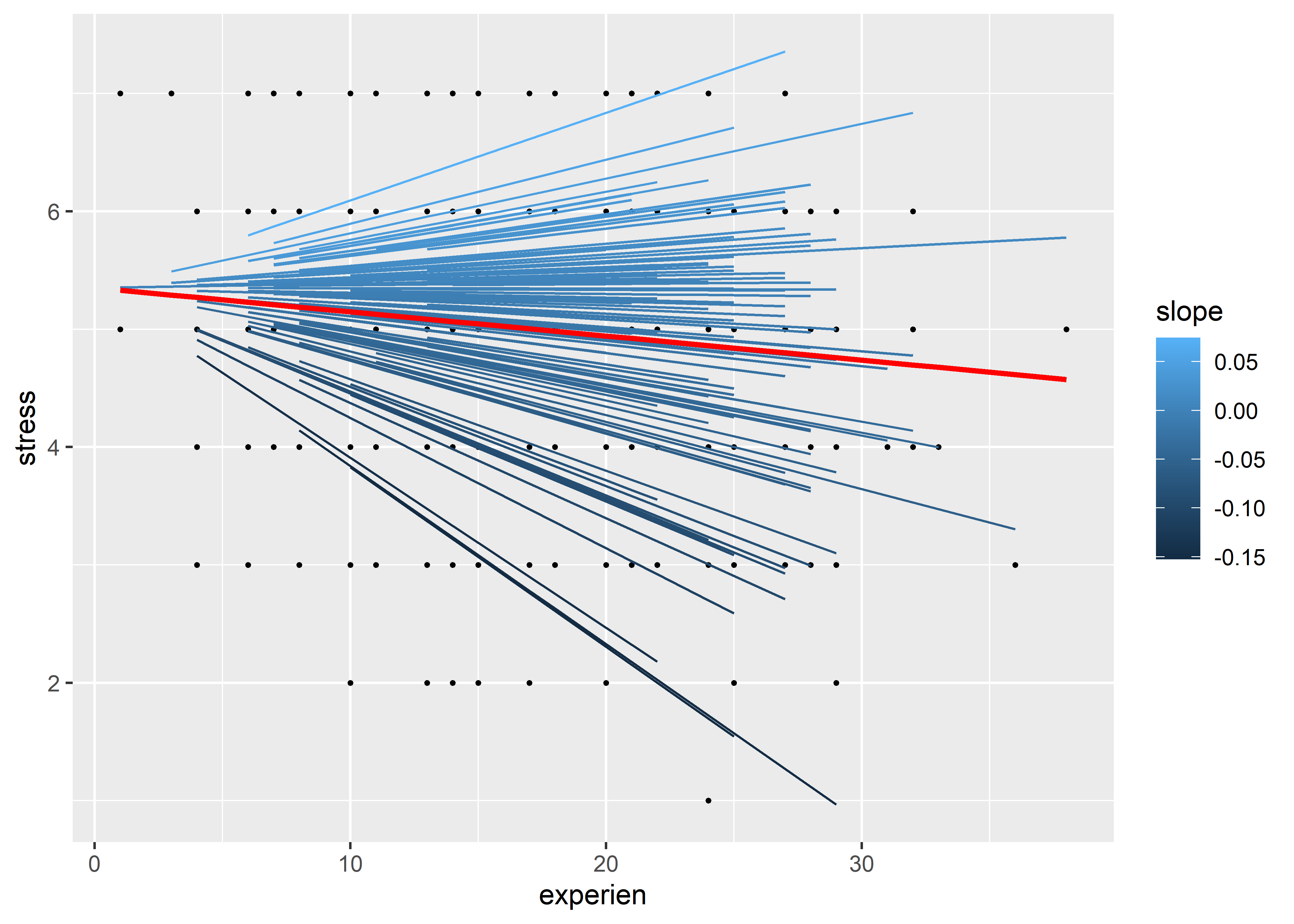
La varianza estimada de los efectos aleatorios del coeficiente de experien es baja con respecto a la residual. Por el contrario, la varianza estimada de los efectos aleatorios del intercepto en el modelo model_ri es más alta que la residual. Esto podría estar indicando que los interceptos aleatorios pueden explicar mejor la variabilidad que los coeficientes aleatorios para la variable experien. En las siguientes secciones veremos maneras más objetivas de evaluar el ajuste de los modelos.
22.5 Pruebas de significancia
Algo que distingue los resultados de la función lmer() con otras funciones vistas previamente para ajustar modelos de regresión es que lmer() no imprime p-valores para las pruebas de significancia de los efectos fijos ni de los aleatorios. Para este tipo de modelos multinivel o jerárquicos, el tema de los p-valores es complejo. La solución más sencilla implica utilizar un método de remuestreo llamado bootstrap para encontrar intervalos de confianza aproximados. Luego, se puede usar estos intervalos de confianza para evaluar la significancia de los efectos. Si el intervalo de confianza contiene al valor 0, entonces se asume que el efecto no es significativo.
Para calcular los intervalos de confianza mediante bootstrap de los efectos de un modelo ajustado con lmer() podemos usar la función confint(). Previamente, debemos haber cargado el paquete lme4. Dentro de confint() debemos agregar el argumento method = "boot" para que calcule los intervalos mediante bootstrap. Además, existen diferentes tipos de bootstrap. Entre los tipos disponibles en están el bootstrap por percentil (perc), el bootstrap por error estándar (basic), y el bootstrap por la distribución normal (norm). Para especificar el tipo de bootstrap usamos el parámtero boot.type. Generalmente, se recomienda hallar todos los tipos de bootstrap para tener una mayo evidencia de la significancia de los efectos. Por ejemplo, para el bootstrap por percentil de los efectos del modelo model_ri_simple:
confint(model_ri_simple, method = "boot", boot.type = "perc")Computing bootstrap confidence intervals ... 2.5 % 97.5 %
.sig01 0.69408745 0.91958745
.sigma 0.50289661 0.55292403
(Intercept) 5.22378534 5.59722681
experien -0.02921801 -0.01756859Esta función imprime los intervalos de confianza para todos los efectos del modelo. .sig01 hace referencia a la varianza de los efectos aleatorios del grupo 1, es decir, a wardid. .sigma, por otro lado, a la varianza residual. Los últimos dos términos corresponden al intercepto y el coeficiente de los años de experiencia.
Cabe resaltar que el bootstrap, por ser un método basado en remuestreo, genera resultados diferentes cada vez que se ejecuta. Obviamente, estos resultados no difieren mucho. Si se quisiera mantener el resultado de una ejecución, tenemos que establecer una semilla para la generación de los números pseudo-aleatorios para el remuestro. Esto lo hacemos ejecutando la función set.seed() antes de confint(). Dentro de la función podemos poner el número entero que deseemos:
Computing bootstrap confidence intervals ... 2.5 % 97.5 %
.sig01 0.7040196 0.9397604
.sigma 0.5053240 0.5555700
(Intercept) 5.2253269 5.6126384
experien -0.0292744 -0.0181235Podemos también usar la función tidy() para obtener los intervalos de confianza en una tabla. Para especificar que queremos calcular los intervalos de confianza agregamos el argumento conf.int = TRUE. Para establecer que queremos usar bootstrap agregamos conf.method = "boot", mientras que para especificar qué tipo de bootstrap usamos el parámetro boot.type:
Computing bootstrap confidence intervals ...
Computing bootstrap confidence intervals ...# A tibble: 4 × 8
effect group term estimate std.error statistic conf.low conf.high
<chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 fixed <NA> (Intercept) 5.41 0.0967 55.9 5.23 5.61
2 fixed <NA> experien -0.0239 0.00294 -8.15 -0.0293 -0.0181
3 ran_pars wardid sd__(Interc… 0.810 NA NA 0.677 0.939
4 ran_pars Residual sd__Observa… 0.530 NA NA 0.506 0.552 Vemos que por más que hemos usado la misma semilla, los intervalos para las varianzas de los efectos aleatorios son diferentes a los encontrados con confint(). La razón es que ambas funciones tienen mecánicas diferentes para ejectuar el bootstrap. Sin embargo, ambos resultados son válidos y no son contradictorios. De estos intervalos podemos concluir que el efecto aleatorio de los pabellones y el efecto fijo de los años de experiencia son significativos bajo el modelo.
Alternativamente, podemos usar el paquete lmerTest para ajustar modelos multinivel que produzcan p-valores para los efectos fijos mediante el método de aproximación de grados de libertad de Satterthwaite. Este paquete contiene una función lmer() igual a la función del paquete lmer4. Por ejemplo, reajustemos el modelo con efectos mixtos model_ri_simple:
library(lmerTest)
model_ri_simple_test <- lmer(stress ~ experien + (1|wardid), data = nurses)
summary(model_ri_simple_test)Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: stress ~ experien + (1 | wardid)
Data: nurses
REML criterion at convergence: 1898.1
Scaled residuals:
Min 1Q Median 3Q Max
-2.8446 -0.6774 -0.0076 0.6692 3.1786
Random effects:
Groups Name Variance Std.Dev.
wardid (Intercept) 0.6557 0.8098
Residual 0.2810 0.5301
Number of obs: 1000, groups: wardid, 100
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 5.408204 0.096663 181.489078 55.949 < 2e-16 ***
experien -0.023925 0.002937 908.271291 -8.146 1.23e-15 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
experien -0.517Vemos que ahora los efectos fijos del intercepto y el coeficiente de los años de experiencia tienen p-valores para evaluar su significancia. En este caso, podemos decir que estos efectos son significativos. Cuando se carga el paquete lmerTest, la función lmer() de este paquete reemplaza a la función del paquete lme4. Sin embargo, lmer() de lme4 es más eficiente computacionalmente que lmer() de lmerTest, por lo que se recomienda usar el primero cuando no es necesario evaluar la significancia.
22.6 Evaluación de modelos
Para comparar modelos multinivel según la calidad del ajuste a los datos se recomienda que los modelos hayan sido ajustados usando MLE (máxima verosimilitud) y no REML (máxima verosimilitud restringida). Recordemos que REML es la opción por defecto de la función lmer().
La función anova() reajusta los modelos con MLE y devuelve medidas de calidad de ajuste como el AIC y el BIC (criterio de información Bayesiano). Además, si los modelos son anidados (la estructura de uno está contenida en el otro), también realiza la prueba de significancia del modelo más complejo. Por ejemplo, para los modelos model_ri y model_ri_simple (agregar primero el menos complejo):
anova(model_ri, model_ri_simple)refitting model(s) with ML (instead of REML)Data: nurses
Models:
model_ri: stress ~ 1 + (1 | wardid)
model_ri_simple: stress ~ experien + (1 | wardid)
npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
model_ri 3 1955.3 1970.0 -974.64 1949.3
model_ri_simple 4 1893.1 1912.8 -942.57 1885.1 64.141 1 1.158e-15 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Vemos que el modelo de efectos mixtos model_ri_simple tiene menor AIC y menor BIC, por lo que tiene una mayor calidad de ajuste. Además, es significativo con respecto al modelo model_ri que solo incluye interceptos aleatorios.
También podemos pasar salid de anova() a una tabla con la función tidy():
model_ri_anova <- anova(model_ri, model_ri_simple)refitting model(s) with ML (instead of REML)tidy(model_ri_anova)# A tibble: 2 × 9
term npar AIC BIC logLik deviance statistic df p.value
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 model_ri 3 1955. 1970. -975. 1949. NA NA NA
2 model_ri_simple 4 1893. 1913. -943. 1885. 64.1 1 1.16e-1522.7 Chequeo de adecuación del modelo
El paquete performance tiene la función check_model() que produce un conjunto de gráficos para evaluar la adecuación de varios tipos de modelos, entre ellos los modelos multinivel. Por ejemplo, para el modelo de efectos mixtos model_ri_simple:
library(performance)
check_model(model_ri_simple)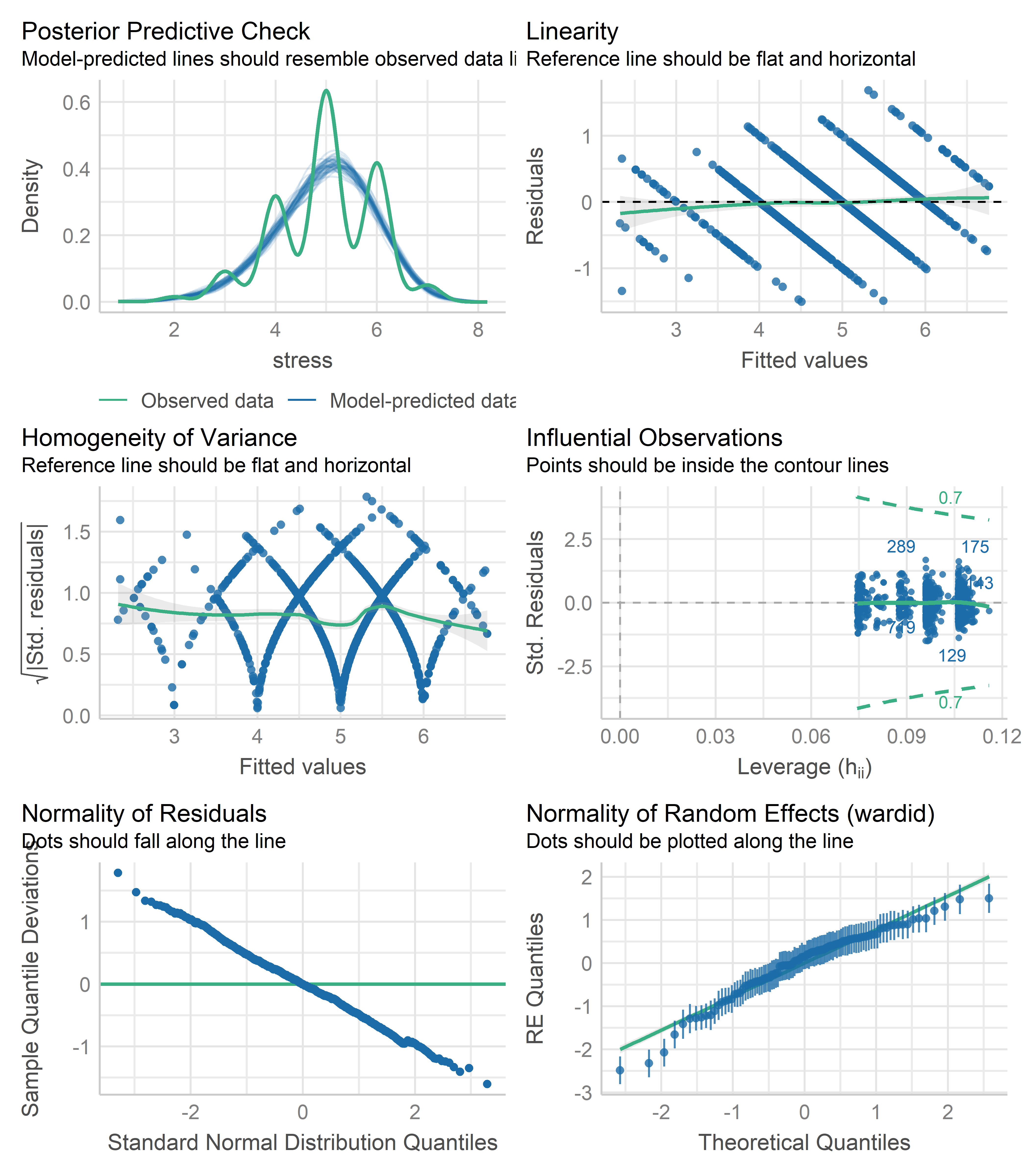
Los gráficos son muy similares a los vistos para los modelos de regresión lineal y logística. Lo adicional para modelos multinivel son los QQ-plot bajo el título de Normality of Random Effects para evaluar la normalidad de los efectos aleatorios por cada factor de agrupación; en este caso, solo se produce un gráfico para wardid. Vemos los efectos aleatorios parecen ajustarse bastante bien a la distribución normal, al igual que los residuales del modelo (Normality of Residuals).
Lo particular de estos gráficos son las extrañas formas de los 3 primeros gráficos Posterior Predictive Check, Linearity y Homogeneity of Variance. Esto se debe a que estos datos toman valores discretos y no continuos. Los patrones que vemos en los gráficos anteriores son producto de la naturaleza discreta de esta variable. Veamos un histograma de stress:
ggplot(data = nurses, aes(stress)) + geom_histogram()`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.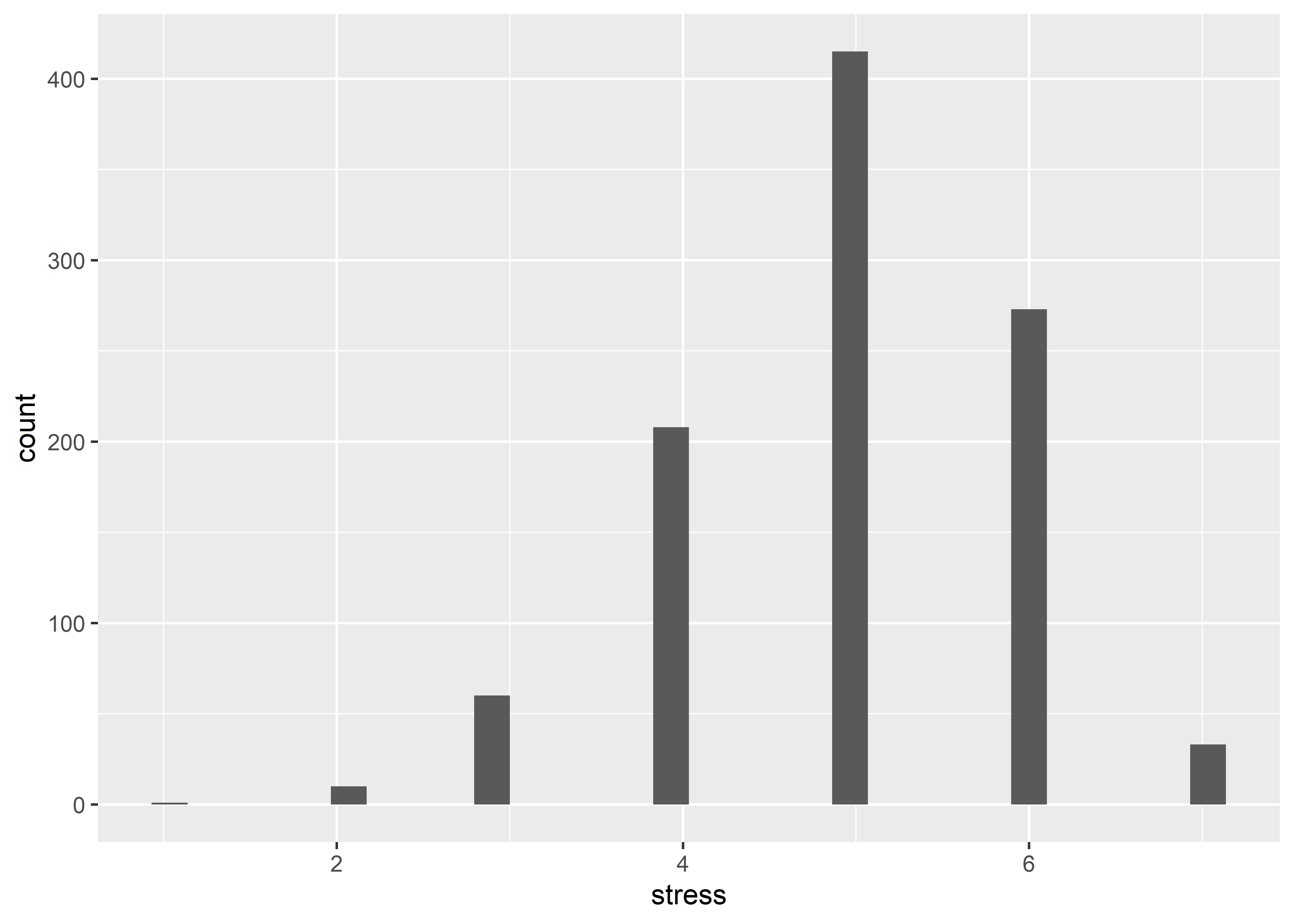
En este histograma podemos apreciar la naturaleza discreta de esta variable. Los modelos que hemos usado hasta ahora asumen que la respuesta es una variable continua; sin embargo, los puntajes tienen un distribución discreta y positiva. Según esta observación, los modelos que estamos viendo en este capítulo puede que no sean los más adecuados para esta respuesta. Aún así, son útiles para explorar las asociaciones de la respuesta y los predictores. Un modelo más adecuado sería un modelo de regresión logística multinivel con respuestas ordinales.
Aparte de esta última observación, no parece haber problemas de heterogeneidad de varianzas o linealidad. Como vimos en el capítulo de chequeo de adecuación para modelos de regresión lineal, es más conveniente usar gráficos de residuales parciales para evaluar la linealidad de un predictor. Por ejemplo, para experien:
library(ggeffects)
pred <- ggpredict(model_ri_simple, "experien [all]")
plot(pred, residuals = TRUE)Data points may overlap. Use the `jitter` argument to add some amount of
random variation to the location of data points and avoid overplotting.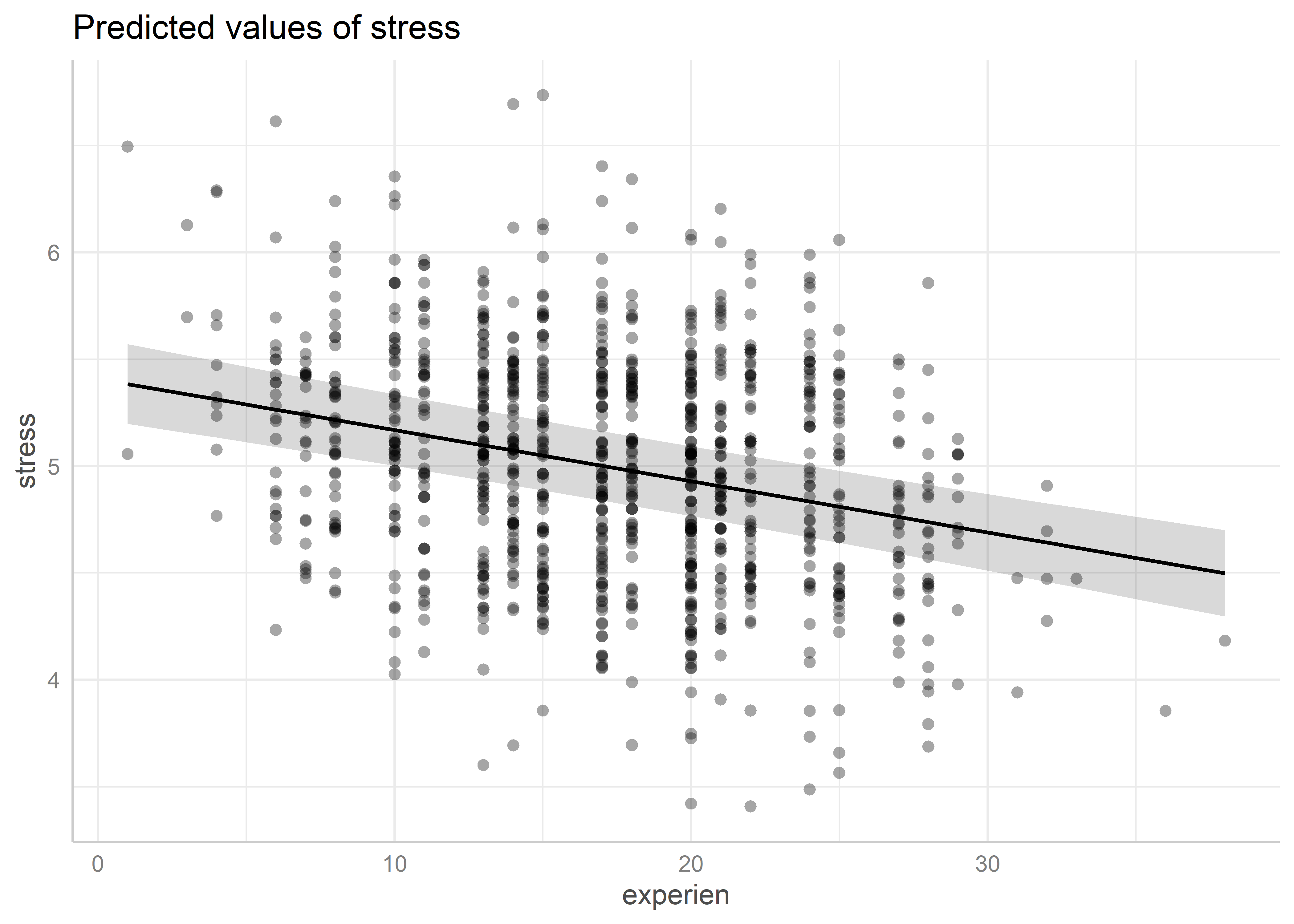
Observamos que no parece haber un patrón no lineal en los residuales parciales del efecto de experien, por lo que podemos decir que este efecto está correctamente especificado.
22.8 Ejercicios
Ejercicio 1
Ajustar un modelo de dos niveles que incluya en el primer nivel el intercepto general y los efectos fijos de de la edad (age), el sexo (gender), y los años de experiencia (experien), mientras que en el segundo nivel dado por el pabellón (wardid) los efectos aleatorios del intercepto y los coeficientes del grupo experimental (expcon) y el tipo de pabellón (wardtype). Probar con las siguientes estructuras para los efectos aleatorios:
- Efectos aleatorios correlacionados para los coeficientes de
expconywardype:(expcon + wardtype|wardid) - Efectos aleatorios no correlacionados para los coeficientes de
expconywardype:(expcon|wardid) + (wardtype|wardid)
Evaluar la significancia de los efectos de los predictores en los modelos.
Ejercicio 2
Construir un modelo de tres niveles con efectos aleatorios para los hospitales y los pabellos dentro de los hospitales. Comparar el coeficiente de correlación interclase y la calidad de ajuste de este modelo con el modelo de dos niveles con interceptos aleatorios para los pabellones. Pista: Para incluir el efecto aleatorio de los hospitales y de los pabellones dentro de cada hospital se usa la sintaxis (1|hospital/ward).
Ejercicio 3
Construir un modelo de tres niveles con efectos fijos para la edad (age), el sexo (gender), los años de experiencia (experien) y el grupo experimental (expcon),y efectos aleatorios para los factores de agrupación, el tipo de pabellón (wardtype) y el tamaño del hospital (hospsize) en sus respectivos niveles. Evaluar la significancia de los efectos fijos y comparar el ajuste de este modelo con el modelo de tres niveles del ejercicio anterior. Considerar efectos aleatorios no correlacionados.