9 Exactitud y precisión
Cuando hacemos estudios observacionales o experimentales, generalmente trabajamos con una muestra de personas y esperamos que, si el estudio ha sido llevado correctamente, podamos extrapolar los resultados de la muestra a la población de interés. Digamos, por ejemplo, que queremos saber el porcentaje de adultos mayores de 18 años que se han hecho un despistaje de VIH en el último año en el departamento de Lima. Para calcular exactamente este porcentaje, tendríamos que consultarle a cada persona de la población si se ha hecho un despistaje de VIH en el último año. El valor que calculemos de toda la población es lo que se llama el parámetro poblacional. Sin embargo, en la práctica es muy difícil, costoso y, muchas veces, ineficiente, trabajar con toda la población. Por esta razón, se utiliza una muestra y de ella se calcula el porcentaje de personas que se ha hecho un despistaje de VIH. A esta cantidad se le llama estadística muestral y sirve para estimar el valor del parámetro poblacional. Sin embargo, el proceso de muestreo siempre va a estar supeditado a tener un grado de incertidumbre y, por tanto, la estadística muestral nunca va a ser exactamente igual al parámetro poblacional. Más aún, es extremadamente difícil conducir un estudio perfecto y otros factores de error pueden afectar la estimación. Por ejemplo, se pueden incluir por error en el estudio personas que no son representativas de la población de interés.
Por otro lado, si pudieramos sacar muchas muestras diferentes y calcular la estadística de cada una, es seguro que estos valores van a diferir de muestra en muestra. A la distribución de probabilidad del conjunto de valores posibles que puede tomar la estadística muestral se le llama distribución muestral. En otras palabras, la distribución muestral describe el conjunto de valores posibles que podría tomar la estadística si pudieramos replicar el proceso de muestreo un número grande de veces. Sin embargo, esto en la práctica no es posible y solo basamos nuestras conclusiones en una muestra. Por lo tanto, nuestra estadística muestral va a estar supeditada a un grado de incertidumbre ya que es solo un valor de todos los valores que puede tomar. Estas discrepancias entre la estadística muestral, el parámetro poblacional, y los diferentes valores que puede tomar la estadística muestral están asociadas a los conceptos de exactitud y precisión. Como veremos más adelante, la exactitud de una estadística muestral se expresa como la diferencia esperada entre esta y el parámetro poblacional, mientras que la precisión de una estadística muestral se expresa como el grado de variabilidad de los posibles valores que esta puede tomar. La distribución muestral de una estadística juega un papel importante para el análisis de exactitud y precisión en el proceso de inferencia estadística.
El proceso de medición puede ser visto también bajo los lentes de la inferencia estadística. Por ejemplo, digamos que quieres medir tu peso usando una balanza digital. Es imposible saber tu peso exactamente y, por tanto, este valor representa el parámetro poblacional que deseas estimar. Cuando haces una medición, la medida resultante representa una estadística muestral. Es muy improbable que este valor sea igual al parámetro poblacional, pero puede estar cerca. Qué tan cerca esté depende de la exactitud de la balanza. La exactitud de la balanza depende bastante de factores físicos. Si, por ejemplo, la balanza está descalibrada, es muy probable que las medidas sean inexactas. Por otro lado, si te pesas todos los días a la misma hora, es seguro que cada medida va a diferir una de otra. Qué tanto difieran va a depender de factores que son muy difíciles de controlar, como la composición corporal, la posición, etc. Cada medición vendría a ser una muestra y la medida una estadística muestral. Si pudieras hacer un número considerable de mediciones, digamos 1000, podríamos construir una distribución muestral y analizar la exactitud y precisión de las mediciones de tu peso con esa balanza digital particular.
9.1 Exactitud y precisión en inferencia estadística
Una analogía práctica del proceso de realizar una estimación o medición es la de jugar al tiro al blanco con flechas. En la Figura 9.1 podemos observar cuatro diferentes escenarios según la exactitud y precisión de nuestros tiros:
De la Figura 9.1 podemos observar lo siguiente:
El escenario del cuadrante superior derecho es el ideal en el que acertamos bastante bien al blanco (fuimos exactos) y nuestros tiros no son tan dispersos (fuimos precisos).
El escenario del cuadrante superior izquierdo, si bien nuestros tiros fueron precisos, estos no dieron en el blanco; es decir, no fuimos exactos. El hecho de no darle al blanco varias veces es un indicio de que existe un factor que sistemáticamente hace que nuestros tiros fallen. Por ejemplo, puede que haya una corriente de aire continua que desvía las flechas hacia la esquina izquierda superior.
En el cuadrante inferior derecho tenemos el escenario en el que nuestros tiros estuvieron bien orientados al blanco; sin embargo, la falta de precisión hizo que estos fueran muy dispersos. Lo que podría estar causando esta dispersión parecería tener un efecto más errático, aleatorio, en nuestros disparos. De repente las flechas tienen deformaciones que pueden ser imperceptibles a simple vista pero que impactan en su aerodinámica.
Por último, el escenario del cuadrante inferior izquierdo corresponde al peor de los casos, en el que no fuimos exactos ni precisos. Se observa tanto una desviación sistemática (inexactitud) como una gran dispersión (imprecisión) en nuestros tiros.
Podríamos decir, entonces, que nuestros tiros fueron exactos si en conjunto estos dieron muy cerca al blanco y que nuestros tiros fueron precisos si estos fueron cercanos entre ellos. Si expresamos estos conceptos en términos de inferencia estadística, podemos decir que:
La exactitud se refiere a qué tan cerca está la media de la distribución muestral de un estimador del verdadero valor del parámetro poblacional. A la diferencia entre el valor esperado de un estimador y el valor de parámetro poblacional se le conoce como sesgo. Mientras el sesgo sea menor, las estimaciones serán más exactas, y viceversa.
La precisión se refiere a qué tan cerca están entre ellos los posibles valores que puede tomar el estimador. Esta variabilidad de valores se expresa comúnmente usando el error estándar, el cual se define como la desviación estándar del estimador. A menor error estándar, mayor precisión de estimación, y viceversa.
La inexactitud resulta de errores sistemáticos, esto es, de errores que afectan a todas las mediciones de la misma manera. Estos errores producen estimaciones o mediciones sesgadas. Algunas causas de errores sistemáticos en estudios epidemiológicos son las siguientes:
- Incluir en el estudio personas que no son representativas de la población de interés.
- Sesgos de muestreo: Cuando sistemáticamente algunas personas de la población tienen mayor o menor probabilidad de ser seleccionadas en la muestra.
- Errores humanos al registrar mediciones o resultados de laboratorio.
- Uso inadecuado de instrumentos de medición o uso de instrumentos descalibrados.
- Administrar el tratamiento equivocado a un grupo de personas.
Por otra lado, la imprecisión resulta de errores aleatorios, aquellos que no se pueden controlar o que son impredecibles. Algunas fuentes de imprecisión en estudios epidemiológicos son las siguientes:
- Tamaño de muestra muy pequeño.
- Variabilidad entre sujetos: Las personas siempre van a ser diferente de otras en diversos aspectos, como por ejemplo su peso, su presión sanguínea e incluso cómo responden a un mismo tratamiento.
- Variabilidad de los sujetos: Por ejemplo, si medimos la presión sanguínea de una persona cada hora, las mediciones van a presentar una variabilidad que resulta de muchos factores externos e internos que son difíciles de controlar, como el estrés, el clima, etc.
- Errores aleatorios de muestreo: Errores aleatorios que son inherentes al proceso de muestreo.
- Los instrumentos de medición también pueden presentar imprecisión debido a factores del ambiente (como la temperatura, humedad, vibraciones mecánicas, etc.), la aleatoriedad inducida físicamente (ruido eléctrico o estática), e incluso la variabilidad inducida por cada operador del instrumento.
9.1.1 Usando la distribución muestral para describir la exactitud y precisión
Veamos algunas simulaciones para entender cómo podemos describir la exactitud y precisión de una estadística usando su distribución muestral. Digamos que queremos conducir un estudio para estimar el peso de una población de personas. Para esto, extraemos una muestra de 100 personas y medimos su peso. El promedio muestral de los pesos medidos vendría a ser la estimación de la media poblacional del peso. Asumamos, solo por fines demostrativos, que el peso de esta población sigue una distribución normal con media
- El primer escenario consistirá en el caso en el que no hay sesgo y la estimaciones son exactas.
- En el segundo escenario incluirémos un error sistemático: Las muestras se sacarán de una población con una media mayor a
- En el tercer escenario también incluirémos el mismo error sistemático, pero en este caso se extraerán muestra de una población con media menor a
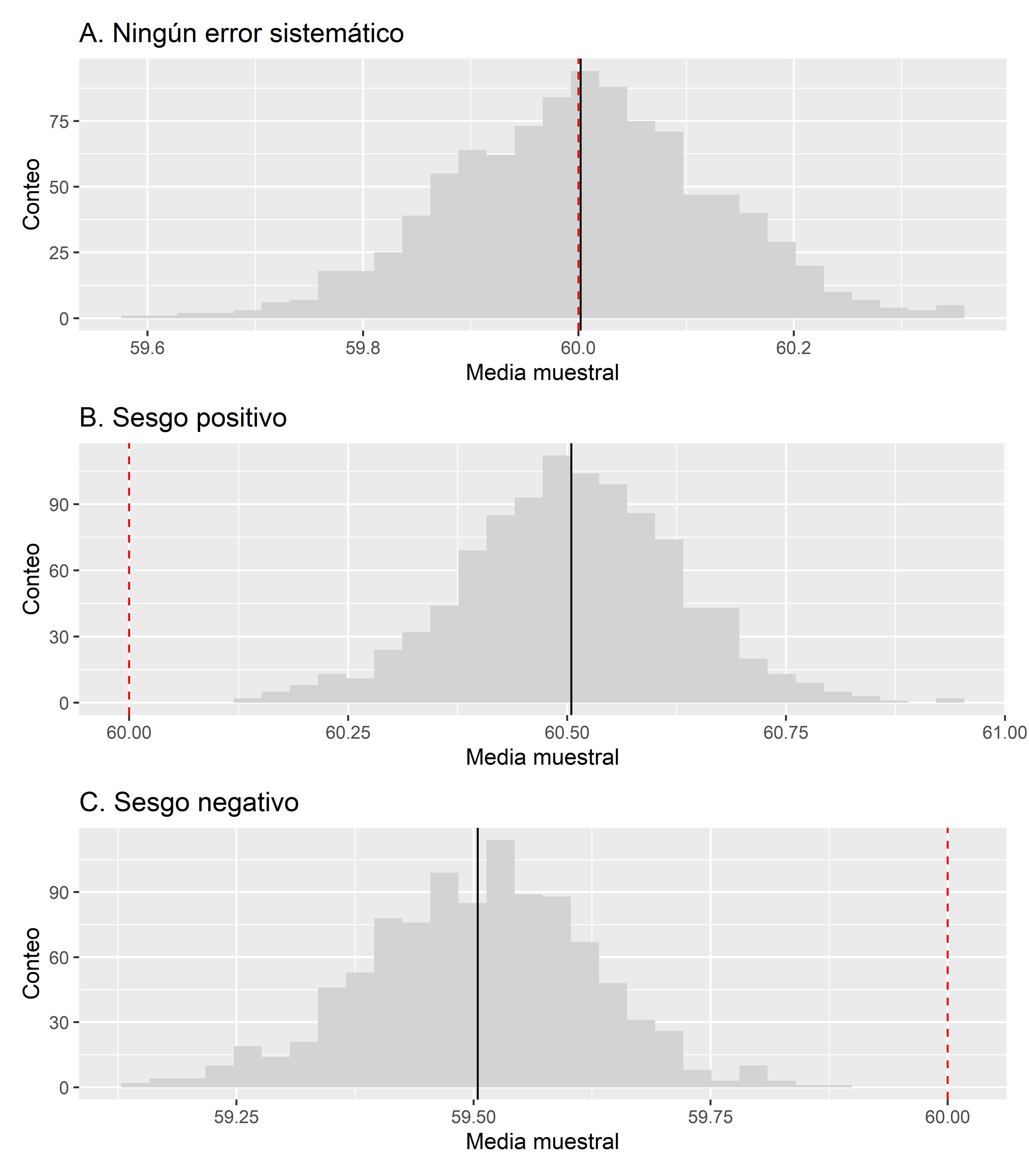
Las distribuciones del promedio muestral en cada uno de los escenarios se pueden ver en la Figura 9.2.
En la Figura 9.2, la línea vertical negra corresponde a la media de los valores del promedio muestral, mientras que la línea roja discontinua corresponde al valor del parámetro
- En el primer escenario A en el que no se añadió ningún error sistemático, la media de la distribución del promedio muestral está bastante próxima a la media poblacional de 60. El sesgo en este caso es de 0.002, un valor bastante pequeño. Podríamos decir que este proceso de estimación ha sido exacto.
- En el segundo escenario B, el error sistemático que se añadió ha hecho que la media del promedio muestral sea mayor a la media poblacional de 60. El sesgo en este caso es de 0.505. El proceso de estimación presenta un sesgo moderado y por tanto no es muy exacto.
- En el tercer escenario C, el error sistemático que se añadió ha hecho que la media del promedio muestral sea menor a la media poblacional de 60. El sesgo en este caso es de -0.496. Al igual que en el segundo escenario, este proceso de estimación presenta un sesgo moderado y por tanto no es muy exacto.
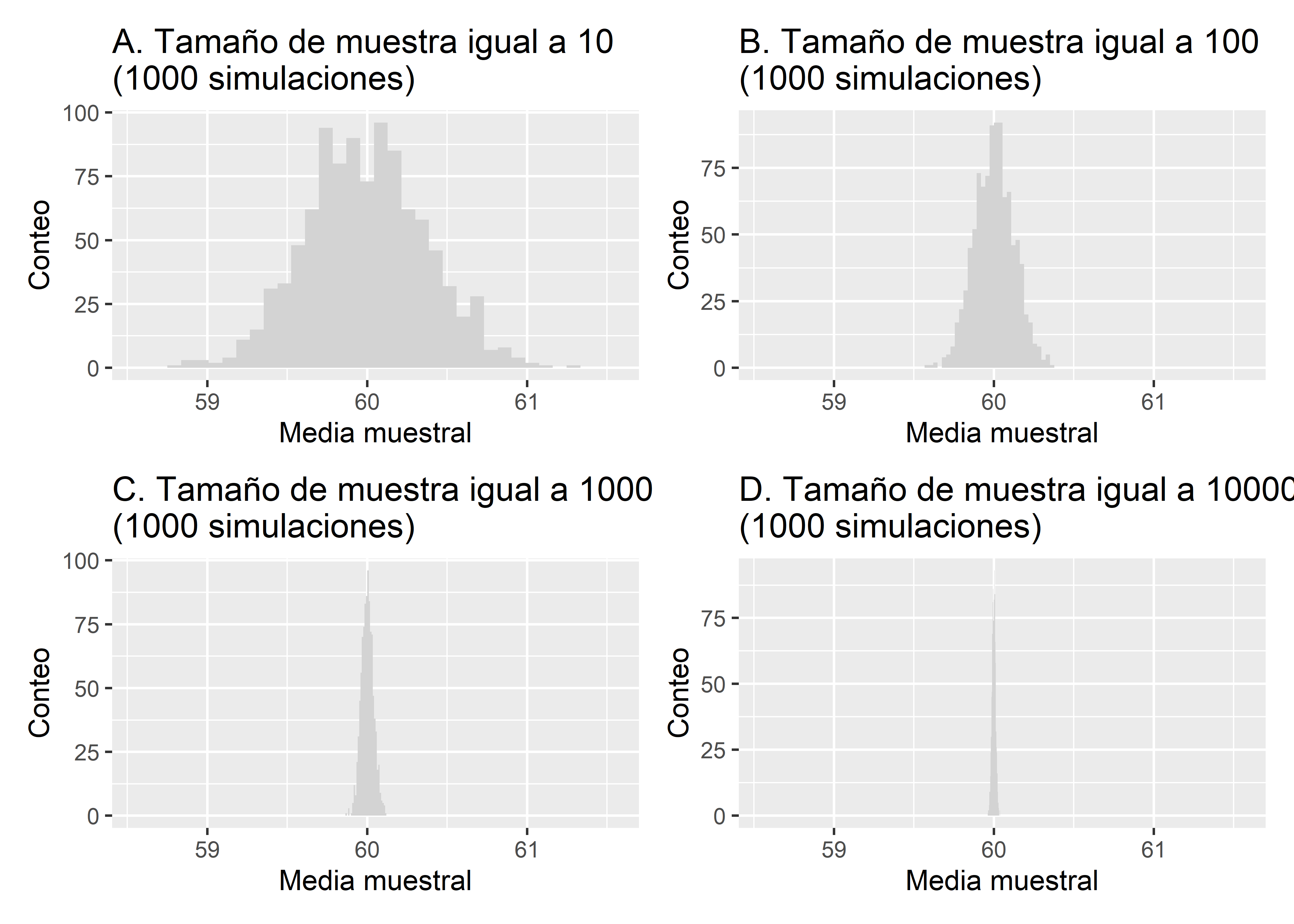
Ahora simulemos la distribución muestral del promedio de los pesos pero con diferentes tamaños muestrales. Recordemos que el tamaño muestral es un factor que afecta la precisión de las estimaciones. Haremos simulaciones para tamaños de muestra de 10, 100, 1000 y 1000.
En la Figura 9.3 podemos ver los resultados de las simulaciones de los tamaños de muestra. Vemos que a medida que aumenta el tamaño, la dispersión de las estimaciones disminuye. Para el caso del tamaño de muestra de 10, el error estándar del promedio fue de 0.378, para el tamaño de 100 el error estándar fue de 0.124, para 1000 fue de 0.038, y por último para 10000 fue de 0.012.
Existen fórmulas para poder estimar el error estándar de muchos estimadores, como el promedio y la varianza muestral. Sin embargo, el sesgo es más complicado de calcular, y se estudia sobre todo de manera teórica para saber si un estimador es sesgado o insesgado. Pero recordemos también que algunas fuentes de errores sistemáticos provienen de desviaciones en el estudio y el uso inadecuado de herramientas de medición.
9.1.2 Estimación del error estándar
En esta sección veremos cómo estimar el error estándar de algunos estimadores comunes en estudios epidemiológicos.
9.1.2.1 Media muestral
El error estándar (
donde
Para ejemplificar el cálculo del error estándar del promedio muestral usaremos el conjunto de datos fev.csv. Este conjunto de datos contiene observaciones del estudio realizado por Tager et al. (1979) donde investigaron el efecto del tabaquismo de los padres en la función pulmonar de niños en East Boston, Massachusetts. La data contiene observaciones sobre la edad (age), el volumen de aire expirado en 1 segundo en litros (fev), altura (hgt), sexo (sex), y estatus de fumador de los padres (smoke). La data fue recuperada de Rosner (2015).
Transformaremos la variable sex a un factor que tenga niveles 0: “Mujer” y 1: “Hombres”.
Asumiendo que los datos en cada grupo por sexo provienen de una muestra aleatoria, calcularemos el promedio muestral de fev y su error estándar en cada uno de ellos.
sample_mean <- fev %>%
group_by(sex) %>%
summarise(
n = n(),
sd = sd(fev),
sample_mean = mean(fev)) %>%
mutate(se = sd / sqrt(n)) %>%
select(-sd)
sample_mean# A tibble: 2 × 4
sex n sample_mean se
<fct> <int> <dbl> <dbl>
1 Mujer 318 2.45 0.0362
2 Hombre 336 2.81 0.0548Podemos decir entonces que la media estimada del volumen de aire expirado en 1 segundo en el grupo de mujeres es de geom_errorbar().
sample_mean %>%
ggplot(aes(x = sex, y = sample_mean, col = sex)) +
geom_point(size = 4) +
geom_errorbar(
aes(ymin = sample_mean - se, ymax = sample_mean + se), width = 0.1
)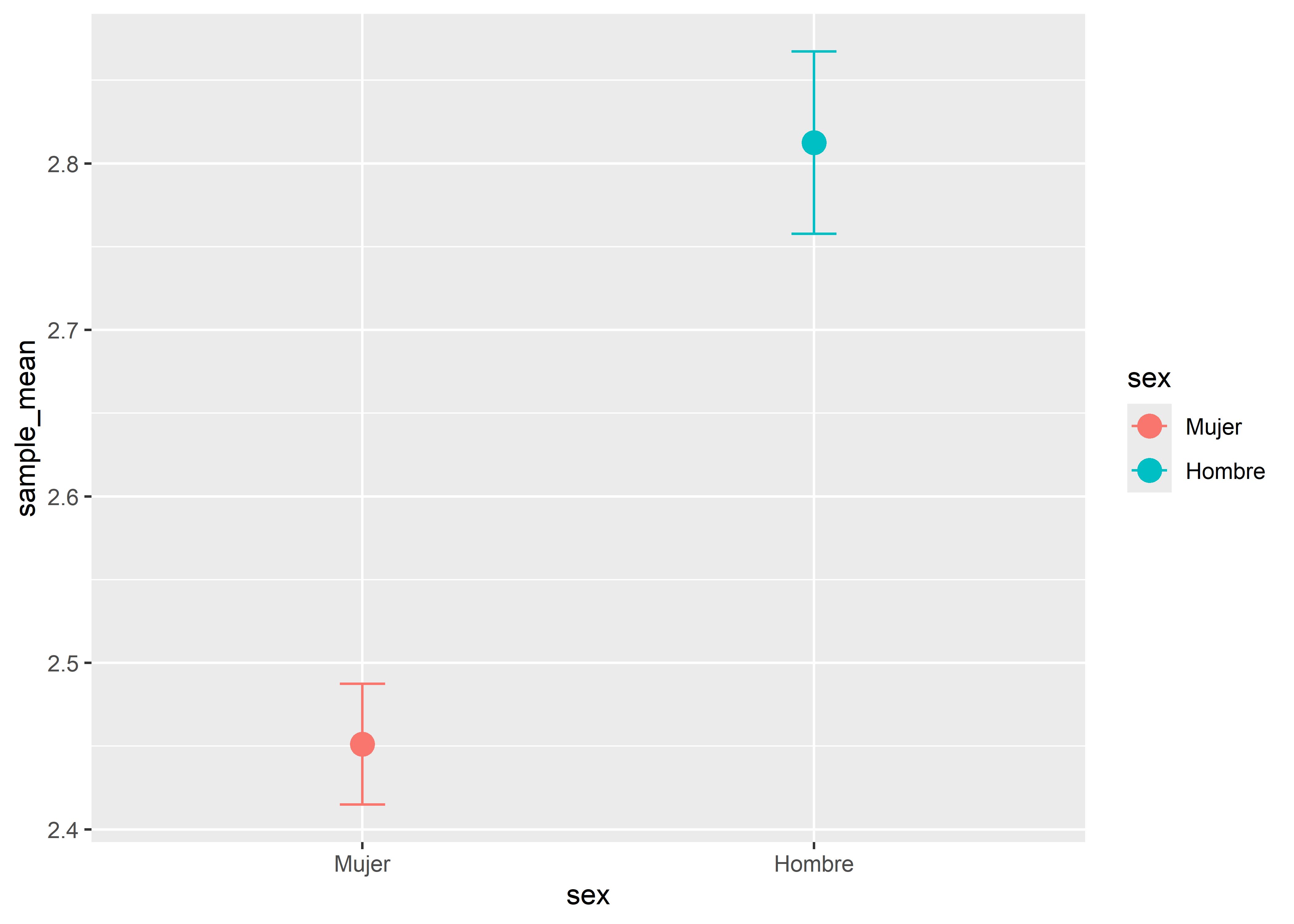
Vemos que la estimación para el grupo de mujeres es ligeramente más precisa ya que su error estándar es menor.
9.1.2.2 Proporción muestral
El error estándar para la proporción muestral
donde
Veamos la proporción muestral de fumadores en los grupos de hombres y de mujeres. Debido a que la variable smoke está codificada con valores numéricos 0 y 1, donde 1 significa que la persona es fumadora y 0 que no, entonces para calcular la proporción de fumadores solo tenemos que sacar el promedio (mean()) de esta variable.
sample_prop <- fev %>%
group_by(sex) %>%
summarise(n = n(), sample_prop = mean(smoke)) %>%
mutate(se = sqrt((sample_prop * (1 - sample_prop)) / n))
sample_prop# A tibble: 2 × 4
sex n sample_prop se
<fct> <int> <dbl> <dbl>
1 Mujer 318 0.123 0.0184
2 Hombre 336 0.0774 0.0146Para mejor interpretación, podemos expresar estas estimaciones como porcentajes. Entonces, diríamos que el porcentaje estimado de fumadores en el grupo de mujeres es de
sample_prop %>%
ggplot(aes(x = sex, y = 100 * sample_prop, col = sex)) +
geom_point(size = 4) +
geom_errorbar(
aes(ymin = 100 * (sample_prop - se), ymax = 100 * (sample_prop + se)),
width = 0.1
)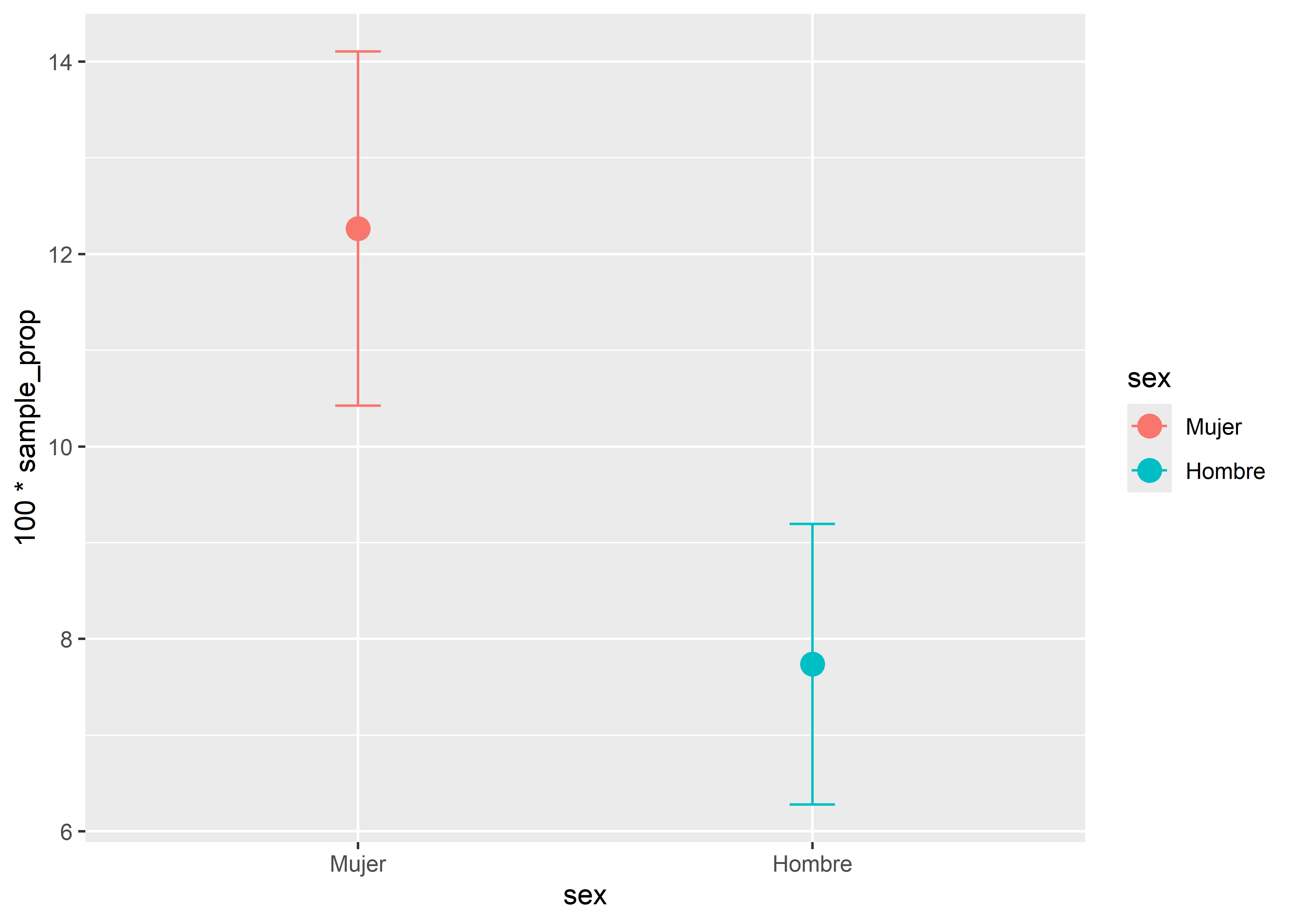
La precisión de estimación es similar en ambos grupos, pero el porcentaje estimado de fumadores es mayor en el grupo de las mujeres que el de los hombres.
9.1.2.3 Tasa estimada de eventos
La tasa estimada de eventos
y su error estándar por
Para la tasa de eventos utilizaremos la data epilepsy del paquete faraway. Este conjunto de datos contiene observaciones de un ensayo clínico de 59 personas con epilepsia. En una primera etapa, se observó por 8 semanas el número de heridas que se hacía cada persona. Luego fueron asignados aleatoriamente a un grupo de tratamiento con la droga Progabide (31 pacientes) o a un grupo placebo (28 pacientes). Por último, se observó el número de heridas luego de 2 semanas.
Usaremos las observaciones de las 2 últimas semanas para evaluar la tasa de heridas por persona a la semana en los grupos de tratamiento y placebo.
Transformaremos la variable treat a un factor que tenga niveles 0: “Placebo” y 1: “Tratamiento” para los que recibieron el tratamiento con la droga Progabide.
En el cálculo del número de mediciones n, multiplicamos el número de registros por 2 para que las tasas estén a nivel semanal.
sample_rate <- epilepsy_treat %>%
group_by(treat) %>%
summarise(n = n() * 2, events = sum(seizures)) %>%
mutate(sample_rate = events / n) %>%
mutate(se = sqrt(sample_rate / n)) %>%
select(-events)
sample_rate# A tibble: 2 × 4
treat n sample_rate se
<fct> <dbl> <dbl> <dbl>
1 Placebo 224 4.30 0.139
2 Tratamiento 248 3.98 0.127Vemos que la tasa estimada de heridas por persona a la semana en el grupo que recibió placebo es de
sample_rate %>%
ggplot(aes(x = treat, y = sample_rate, col = treat)) +
geom_point(size = 4) +
geom_errorbar(
aes(ymin = sample_rate - se, ymax = sample_rate + se), width = 0.1
)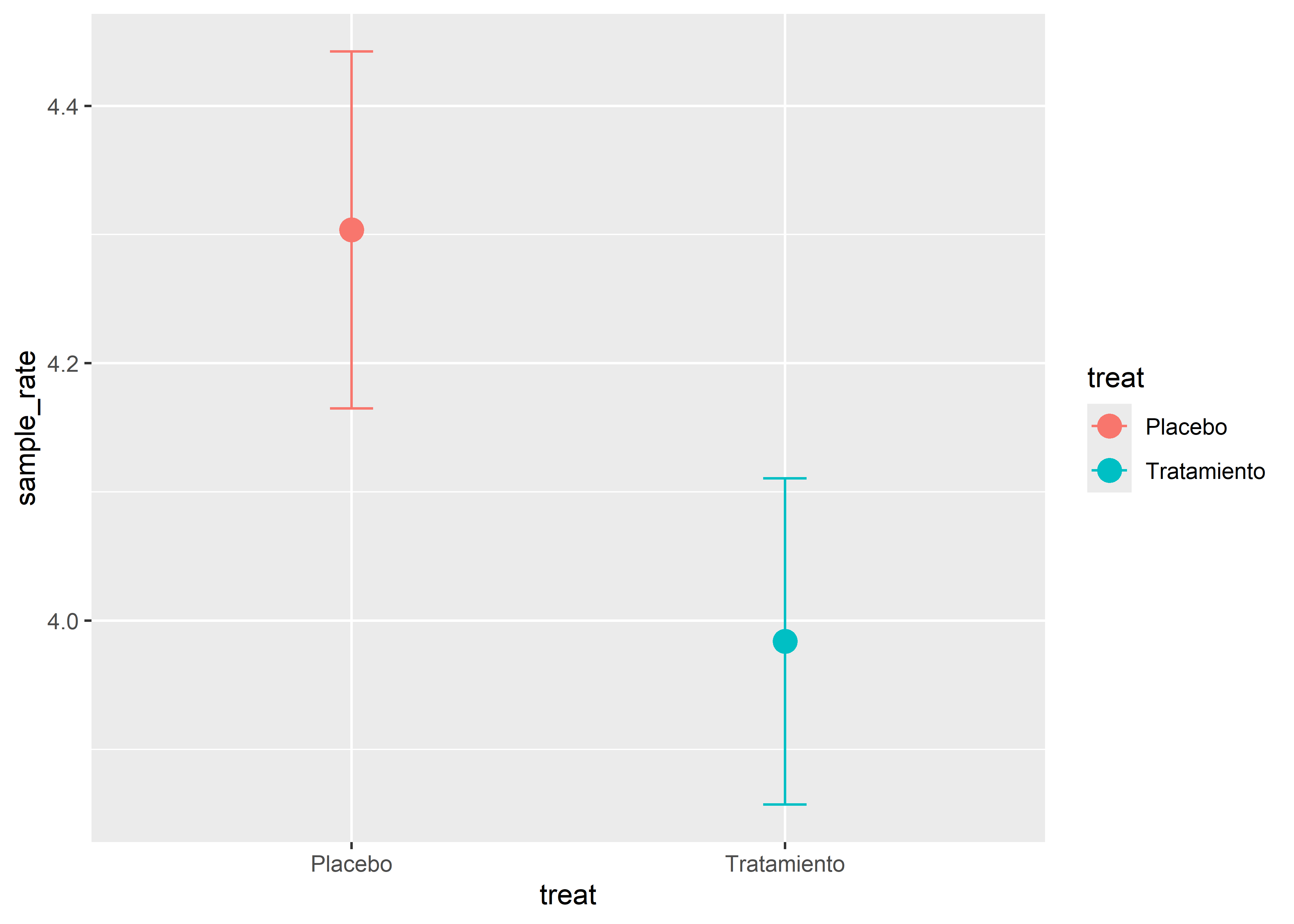
La precisión de ambas estimaciones es muy similar, pero la tasa estimada es mayor en el grupo que recibió el placebo.
9.1.2.4 Modelo de regresión lineal
Usaremos un modelo de regresión lineal usando la variable fev como variable de respuesta y las variables hgt, age y sex como predictores para mostrar cómo calcular el error estándar de las estimaciones de un modelo estadístico. Para una introducción más completa de estos modelos, ver {#sec-regresion-lineal}.
Para ajustar un modelo de regresión lineal en R, usamos la función lm():
Call:
lm(formula = fev ~ hgt + age + sex, data = fev)
Residuals:
Min 1Q Median 3Q Max
-1.37613 -0.24834 0.01051 0.25748 1.94538
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.448560 0.222966 -19.952 < 2e-16 ***
hgt 0.104560 0.004756 21.986 < 2e-16 ***
age 0.061364 0.009069 6.766 2.96e-11 ***
sexHombre 0.161112 0.033125 4.864 1.45e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4126 on 650 degrees of freedom
Multiple R-squared: 0.7746, Adjusted R-squared: 0.7736
F-statistic: 744.6 on 3 and 650 DF, p-value: < 2.2e-16En la sección Coefficients de la impresión de resultados del ajuste podemos ver la estimación de los coeficientes de regresión bajo la columna Estimate y sus errores estándar bajo la columna Std. Error. Por ejemplo, el coeficiente estimado del predictor hgt es 0.10 y su error estándar de 0.005. Para convertir estos resultados a formato tidy, podemos usar la función tidy() del paquete broom. Esta función transforma los outputs de muchas funciones base a formato tidy.
# A tibble: 4 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -4.45 0.223 -20.0 1.88e-69
2 hgt 0.105 0.00476 22.0 1.59e-80
3 age 0.0614 0.00907 6.77 2.96e-11
4 sexHombre 0.161 0.0331 4.86 1.45e- 6Ya que los predictores numéricos están en diferentes escalas, para poder comparar los coeficientes y sus errores estándar necesitamos estimar los coeficientes estandarizados. Para esto, podemos estandarizar los predictores numéricos y volver a ajustar el modelo:
fev_std <- fev %>%
mutate(across(c(hgt, age), \(x) as.vector(scale(x))))
fit_std <- lm(fev ~ hgt + age + sex, data = fev_std)
summary(fit_std)
Call:
lm(formula = fev ~ hgt + age + sex, data = fev_std)
Residuals:
Min 1Q Median 3Q Max
-1.37613 -0.24834 0.01051 0.25748 1.94538
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.55401 0.02345 108.912 < 2e-16 ***
hgt 0.59636 0.02712 21.986 < 2e-16 ***
age 0.18126 0.02679 6.766 2.96e-11 ***
sexHombre 0.16111 0.03312 4.864 1.45e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4126 on 650 degrees of freedom
Multiple R-squared: 0.7746, Adjusted R-squared: 0.7736
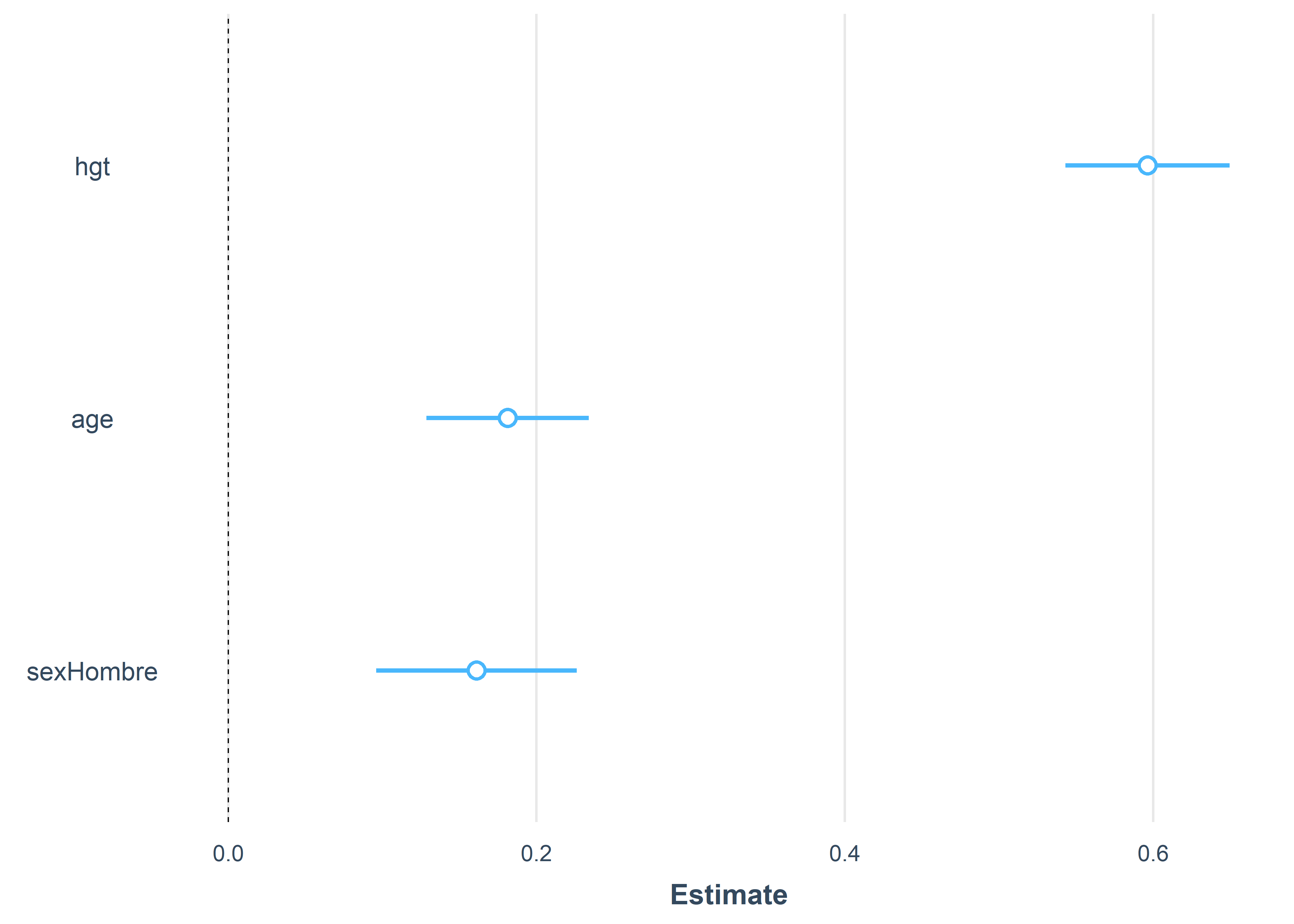
F-statistic: 744.6 on 3 and 650 DF, p-value: < 2.2e-16De esta manera, podemos contruir un forest plot para comparar los coeficientes estimados usando los errores estándar usando algunas funciones de ayuda del paquete broom.helpers:
library(broom.helpers)
fit_std %>%
tidy_and_attach() %>%
tidy_remove_intercept() %>%
ggplot(
aes(
x = variable, y = estimate, ymin = estimate - std.error,
ymax = estimate + std.error, color = variable
)
) +
geom_point() +
geom_errorbar(width = 0.1) +
geom_hline(yintercept = 0, linetype = 2) +
coord_flip() +
theme(legend.position = "none")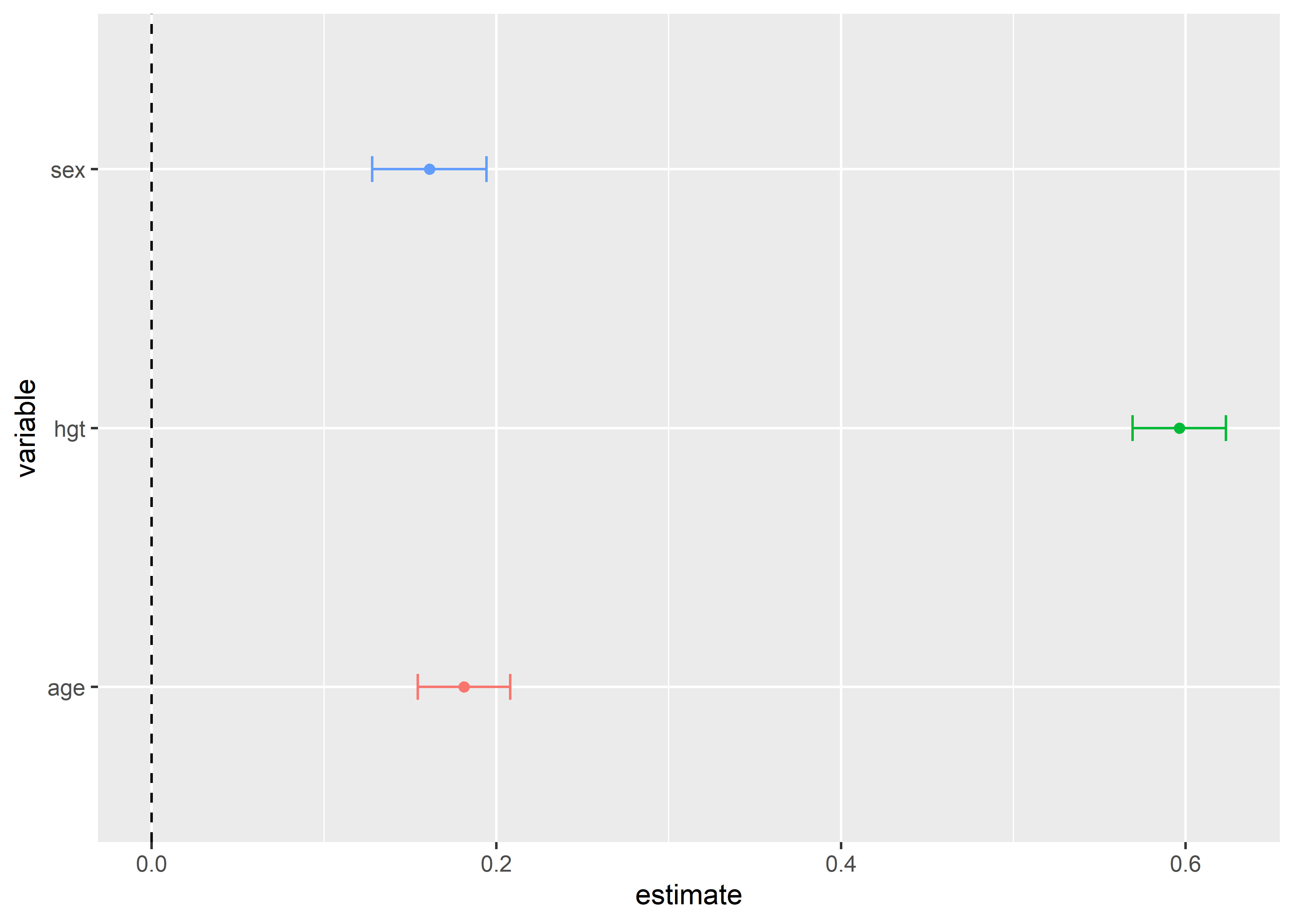
9.1.3 Intervalos de confianza
Otra forma de expresar la precisión de un estimador es usando un intervalo de confianza. Un intervalo al
La regla para calcular un intervalo de confianza depende de lo que queremos estimar. La evaluación de una regla en la muestra nos permitirá calcular dos valores,
Por otro lado, el nivel de confianza
En las siguientes secciones veremos las reglas para estimar los intervalos de confianza de la media, la proporción y la tasa de eventos.
9.1.3.1 Media poblacional
El intervalo al
donde
Usaremos las funciones para pruebas de significancia del paquete rstatix para generar los intervalos al 95% de confianza.
En el caso de la media poblacional, podemos usar la función t_test() con el argumento detailed = TRUE para generar los intervalos de confianza por grupo de sex.
mean_ci <- fev %>%
group_by(sex) %>%
t_test(fev ~ 1, detailed = TRUE) %>%
select(sex, estimate, conf.low, conf.high)
mean_ci# A tibble: 2 × 4
sex estimate conf.low conf.high
<fct> <dbl> <dbl> <dbl>
1 Mujer 2.45 2.38 2.52
2 Hombre 2.81 2.70 2.92Vemos que el intervalo al 95% de confianza observado para la media del volumen de aire expirado en 1 segundo para el grupo de mujeres es geom_pointrange().
mean_ci %>%
ggplot(aes(x = sex, y = estimate, color = sex)) +
geom_point(size = 4) +
geom_pointrange(aes(ymin = conf.low, ymax = conf.high))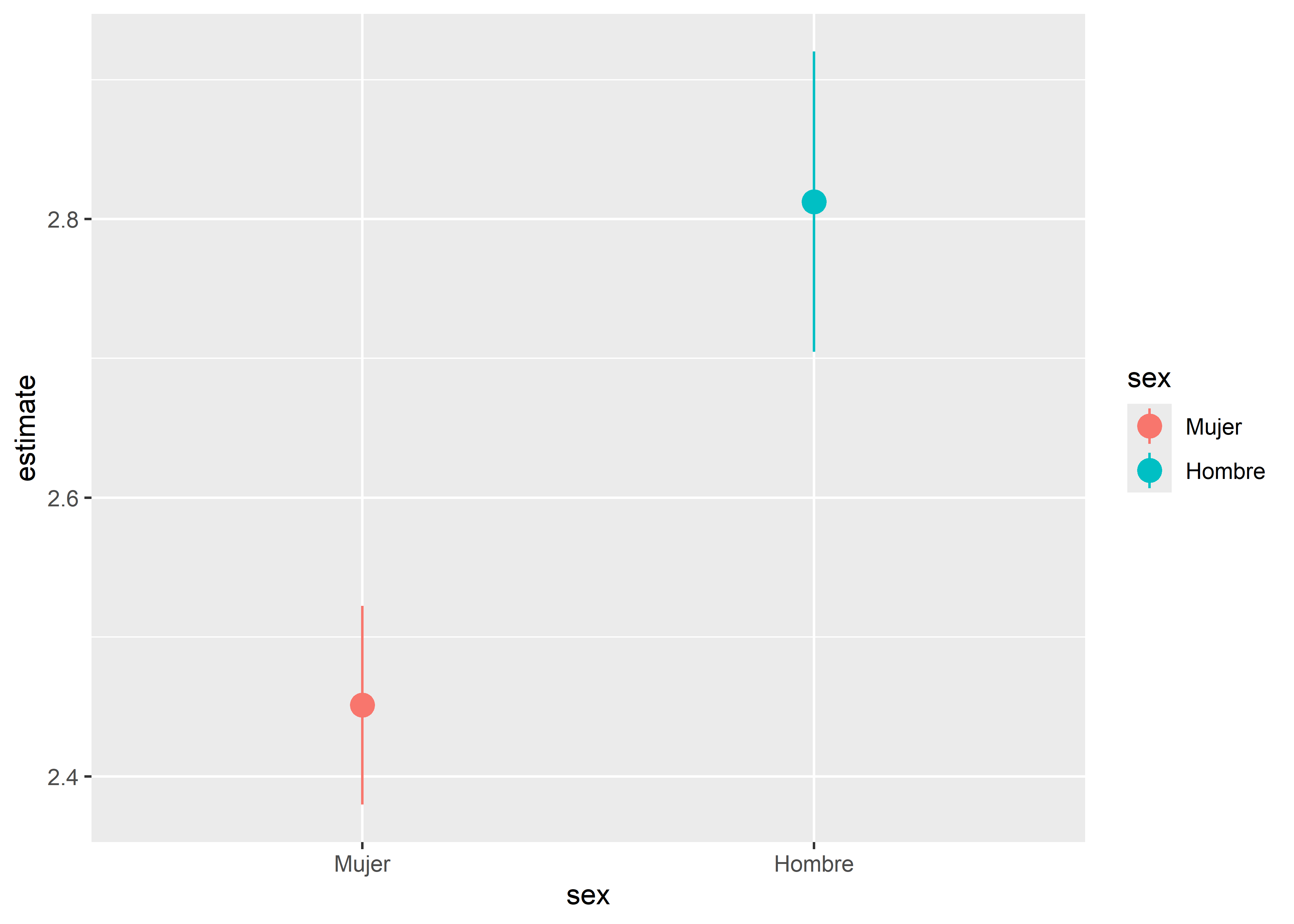
Vemos que el intervalo de confianza para la media del volumen de aire expirado en 1 segundo es ligeramente más angosto para el grupo de mujeres, por lo tanto podríamos decir que la estimación para este grupo es un poco más precisa.
9.1.3.2 Proporción poblacional
La aproximación normal del intervalo al
donde
Calculemos la cantidad de fumadores y el tamaño de cada grupo.
# A tibble: 2 × 3
sex count n
<fct> <dbl> <int>
1 Mujer 39 318
2 Hombre 26 336Para el caso de proporciones, rstatix tiene la función prop_test(). Esta función recibe como primer argumento el número de eventos (cantidad de fumadores), y para el segundo, el número total de ensayos (tamaño de cada grupo). Primero, obtendremos el intervalo de confianza para el grupo de mujeres utilizando los cálculos anteriores.
prop_ci_females <- prop_test(x = 39, n = 318, detailed = TRUE) %>%
select(estimate, conf.low, conf.high)
prop_ci_females# A tibble: 1 × 3
estimate conf.low conf.high
<dbl> <dbl> <dbl>
1 0.123 0.0897 0.165El intervalo al 95% de confianza para el porcentaje de fumadores en el grupo de mujeres es
prop_ci_males <- prop_test(x = 26, n = 336, detailed = TRUE) %>%
select(estimate, conf.low, conf.high)
prop_ci_males# A tibble: 1 × 3
estimate conf.low conf.high
<dbl> <dbl> <dbl>
1 0.0774 0.0521 0.113El intervalo al 95% de confianza para el porcentaje de fumadores en el grupo de hombres es
Ahora, creamos una lista con los resultados en ambos grupos y los nombramos como los niveles de sex y unimos ambos data frames por las filas usando la función bind_rows() del paquete dplyr:
prop_ci_list <- list("Mujer" = prop_ci_females, "Hombre" = prop_ci_males)
prop_ci <- bind_rows(prop_ci_list, .id = "sex")
prop_ci# A tibble: 2 × 4
sex estimate conf.low conf.high
<chr> <dbl> <dbl> <dbl>
1 Mujer 0.123 0.0897 0.165
2 Hombre 0.0774 0.0521 0.113Grafiquemos los intervalos de confianza para cada grupo.
prop_ci %>%
ggplot(aes(x = sex, y = 100 * estimate, col = sex)) +
geom_point(size = 4) +
geom_pointrange(aes(ymin = 100 * conf.low, ymax = 100 * conf.high))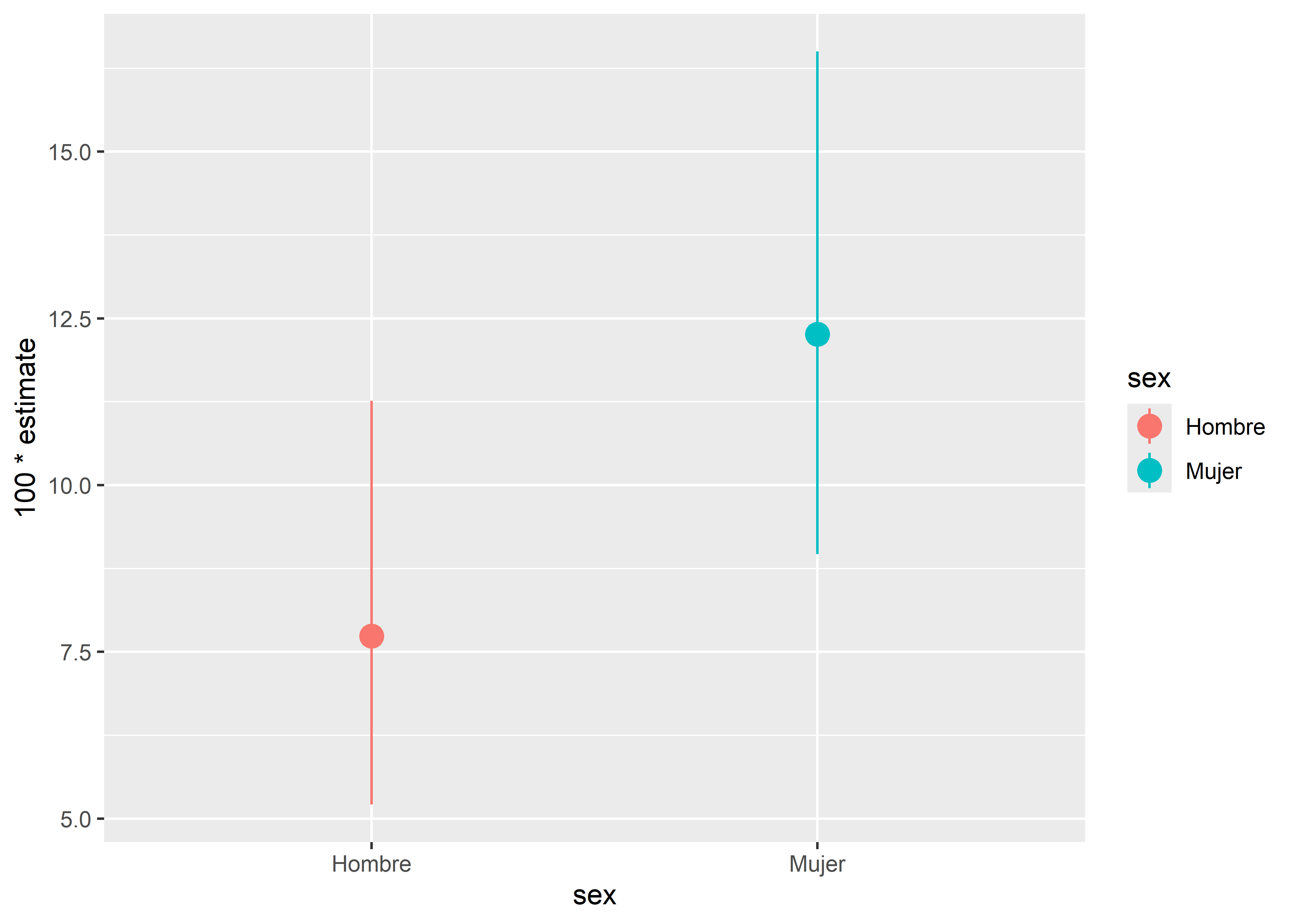
No parece haber mucha diferencia entre las longitudes de los intervalos, aunque el del grupo de mujeres es un ligeramente más amplio, y por tanto menos preciso.
La estimación de una proporción consiste en considerar que el número total de éxitos en la muestra tiene una distribución binomial con probabilidad de éxito igual a la proporción de éxitos en la población. Otra forma de construir un intervalo de confianza es considerando la distribución binomial para el cálculo y no la aproximación normal. A este método se le llama método exacto.
El intervalo exacto al
Para calcular los intervalos con el método exacto podemos usar la función binom_test(). Realizamos el mismo procedimiento que usamos para prop_test() para obtener los intervalos de confianza para cada grupo.
prop_exact_ci_female <- binom_test(x = 39, n = 318, detailed = TRUE) %>%
select(estimate, conf.low, conf.high)
prop_exact_ci_male <- binom_test(x = 26, n = 336, detailed = TRUE) %>%
select(estimate, conf.low, conf.high)
prop_exact_ci_list <- list(
"Mujer" = prop_exact_ci_female, "Hombre" = prop_exact_ci_male
)
prop_exact_ci <- bind_rows(prop_exact_ci_list, .id = "sex")
prop_exact_ci# A tibble: 2 × 4
sex estimate conf.low conf.high
<chr> <dbl> <dbl> <dbl>
1 Mujer 0.123 0.0887 0.164
2 Hombre 0.0774 0.0512 0.111El intervalo al 95% de confianza exacto para el porcentaje de fumadores en el grupo de mujeres es
9.1.3.3 Tasa de eventos
Al igual que en el caso de la proporción, el intervalo de confianza para la tasa de eventos se pude calcular usando una aproximación normal o el método exacto.
La aproximación normal del intervalo al
donde
Volvemos ahora a los datos sobre el ensayo clínico sobre pacientes con epilepsia. No hay una función para calcular la aproximación normal de los intervalos de confianza para tasas de eventos, así que calcularemos los límites para cada grupo de tratamiento manualmente utilizando los resultados almacenados en el objeto sample_rate.
rate_ci <- sample_rate %>%
mutate(
conf.low = sample_rate - qnorm(0.975) * se,
conf.high = sample_rate + qnorm(0.975) * se
) %>%
select(treat, sample_rate, conf.low, conf.high)
rate_ci# A tibble: 2 × 4
treat sample_rate conf.low conf.high
<fct> <dbl> <dbl> <dbl>
1 Placebo 4.30 4.03 4.58
2 Tratamiento 3.98 3.74 4.23El intervalo al 95% de confianza para la tasa de heridas por paciente a la semana en el grupo que no recibió el tratamiento es
Comparemos gráficamente los intervalos.
rate_ci %>%
ggplot(aes(x = treat, y = sample_rate, col = treat)) +
geom_point(size = 4) +
geom_pointrange(aes(ymin = conf.low, ymax = conf.high))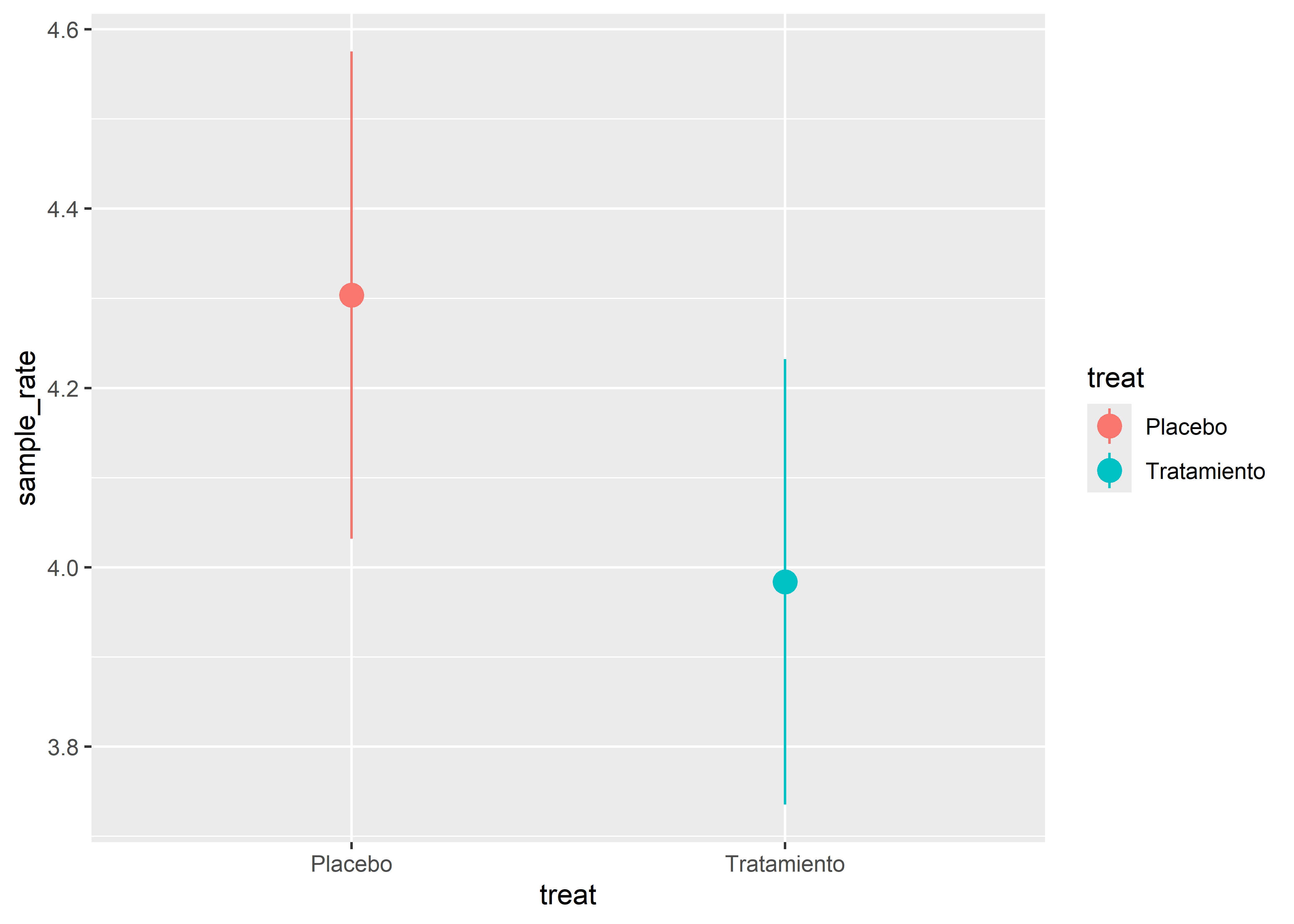
No parece haber mucha diferencia entre la amplitud de los intervalos, aunque para el grupo de tratamiento es un poco más angosta, también debido a que el tamaño de muestra en ese grupo es mayor.
Por otro lado, el intervalo exacto al
donde
Para poder calcular el intervalo de confianza exacto, necesitamos la función base poisson.test(). Esta función devuelve los resultados de realizar una prueba exacta para una variable que se asume tiene una distribución de Poisson. Usamos la función tidy() para obtener tablas de los resultados de luego de poisson.test() y unimos las tablas:
rate_exact_ci_placebo <- poisson.test(x = 964, T = 224) %>%
tidy() %>%
select(estimate, conf.low, conf.high)
rate_exact_ci_treat <- poisson.test(x = 988, T = 248) %>%
tidy() %>%
select(estimate, conf.low, conf.high)
rate_exact_ci_list <- list(
"Placebo" = rate_exact_ci_placebo, "Tratamiento" = rate_exact_ci_treat
)
rate_exact_ci <- bind_rows(rate_exact_ci_list, .id = "treat")
rate_exact_ci# A tibble: 2 × 4
treat estimate conf.low conf.high
<chr> <dbl> <dbl> <dbl>
1 Placebo 4.30 4.04 4.58
2 Tratamiento 3.98 3.74 4.24El intervalo exacto al 95% de confianza para la tasa de heridas por paciente a la semana en el grupo que no recibió el tratamiento es
9.1.3.4 Modelo de regresión lineal
En el caso de regresión, podemos usar la función base confint() para calcular el intervalo de confianza de las estimaciones de los coeficientes de regresión:
confint(fit) 2.5 % 97.5 %
(Intercept) -4.88638016 -4.0107390
hgt 0.09522127 0.1138980
age 0.04355500 0.0791726
sexHombre 0.09606721 0.2261569Además, podemos usar la función tidy() con el argumento conf.int = TRUE para que muestre los intervalos de confianza en una tabla junto con los demás resultados:
tidy(fit, conf.int = TRUE)# A tibble: 4 × 7
term estimate std.error statistic p.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -4.45 0.223 -20.0 1.88e-69 -4.89 -4.01
2 hgt 0.105 0.00476 22.0 1.59e-80 0.0952 0.114
3 age 0.0614 0.00907 6.77 2.96e-11 0.0436 0.0792
4 sexHombre 0.161 0.0331 4.86 1.45e- 6 0.0961 0.226 Podemos usar las estimaciones de los coeficientes estandarizados para comparar los intervalos de confianza de los predictores:
fit_std %>%
tidy_and_attach(conf.int = TRUE) %>%
tidy_remove_intercept() %>%
ggplot(
aes(
x = variable, y = estimate, ymin = conf.low, ymax = conf.high,
color = variable
)
) +
geom_hline(yintercept = 0, linetype = 2) +
geom_pointrange() +
coord_flip() +
theme(legend.position = "none")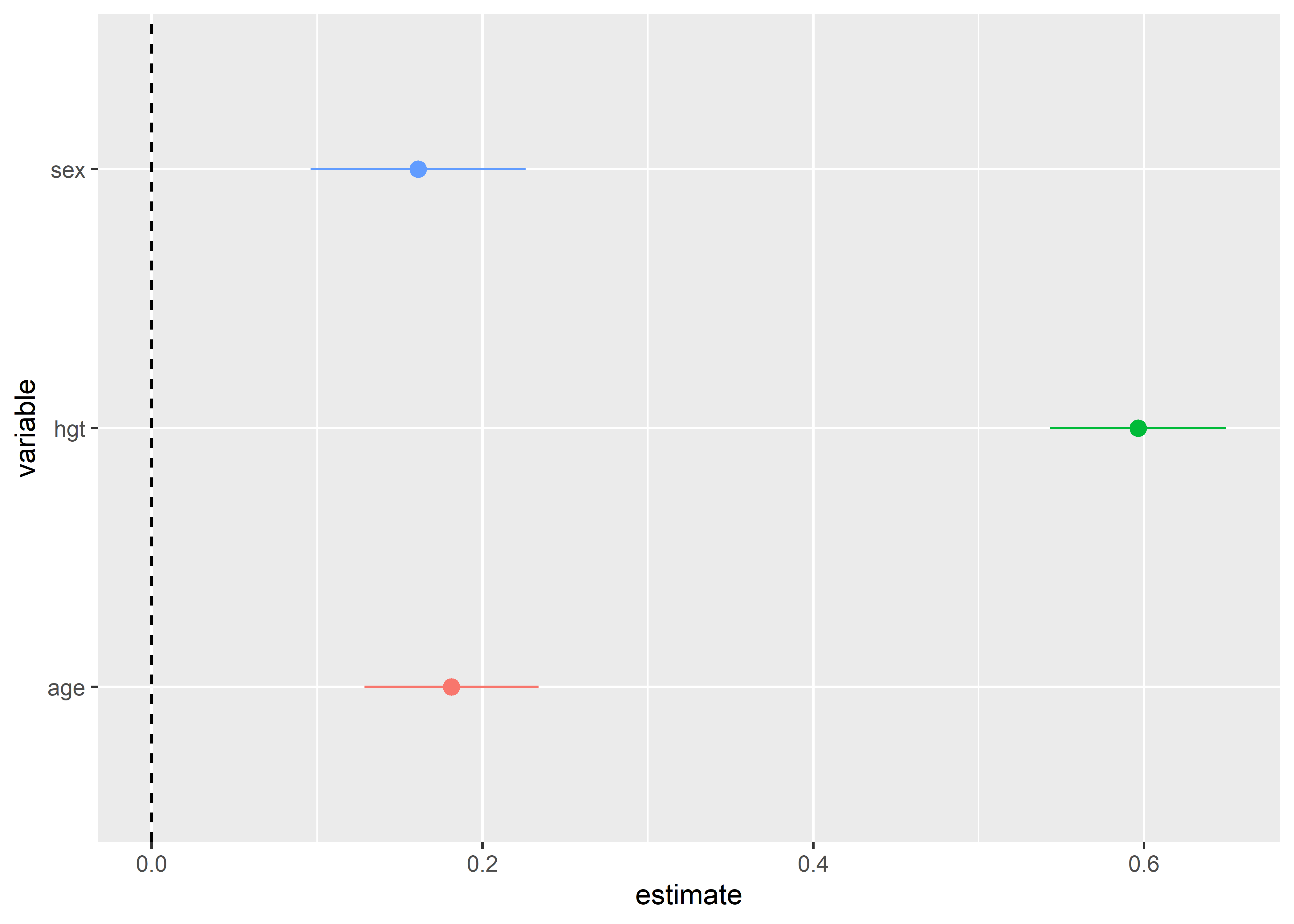
Otro paquete que permite crear estos gráficos es el paquete jtools. La función plot_summs() permite generar forest plots con coeficientes estandarizados sin tener que reajustar el modelo, solo usamos el argumento scale = TRUE:
9.2 Exactitud y precisión en predicción
En un estudio de predicción buscamos un modelo estadístico que nos permita predecir el peso, por ejemplo, de las personas de una población. También podríamos estar interesados en clasificar personas según su riesgo de tener alguna enfermedad. Para esto podemos usar un modelo estadístico sobre alguna prueba de diagnótico. El objetivo de estos estudios es medir qué tan bien estas herramientas predicen un valor numérico o una categoría en la población. Esto difiere del proceso de inferencia estadística, ya que en este último solo buscamos una estimación para una un parámetro poblacional.
El error medio de predicción de un modelo estadístico puede descomponerse en las siguientes cantidades:
El sesgo es el error que surge por usar modelos muy simples para predecir observaciones que provienen de un sistema más complejo. Por ejemplo, el modelo de regresión lineal asume una asociación lineal entre la variable de respuesta y los predictores, pero en la realidad esta asociación puede ser más complicada. Por otro lado, la varianza del modelo se refiere a qué tanto el modelo cambia si se se introducen cambios en los datos. Por último,
Ya que no podemos reducir la varianza del error aleatorio, lo ideal sería reducir el sesgo y la varianza del modelo. Sin embargo, esto es una tarea difícil ya que, generalmente, cuando queremos disminuir el sesgo, la varianza del modelo aumenta, y viceversa. A este dilema se le conoce como el bias-variance tradeoff.
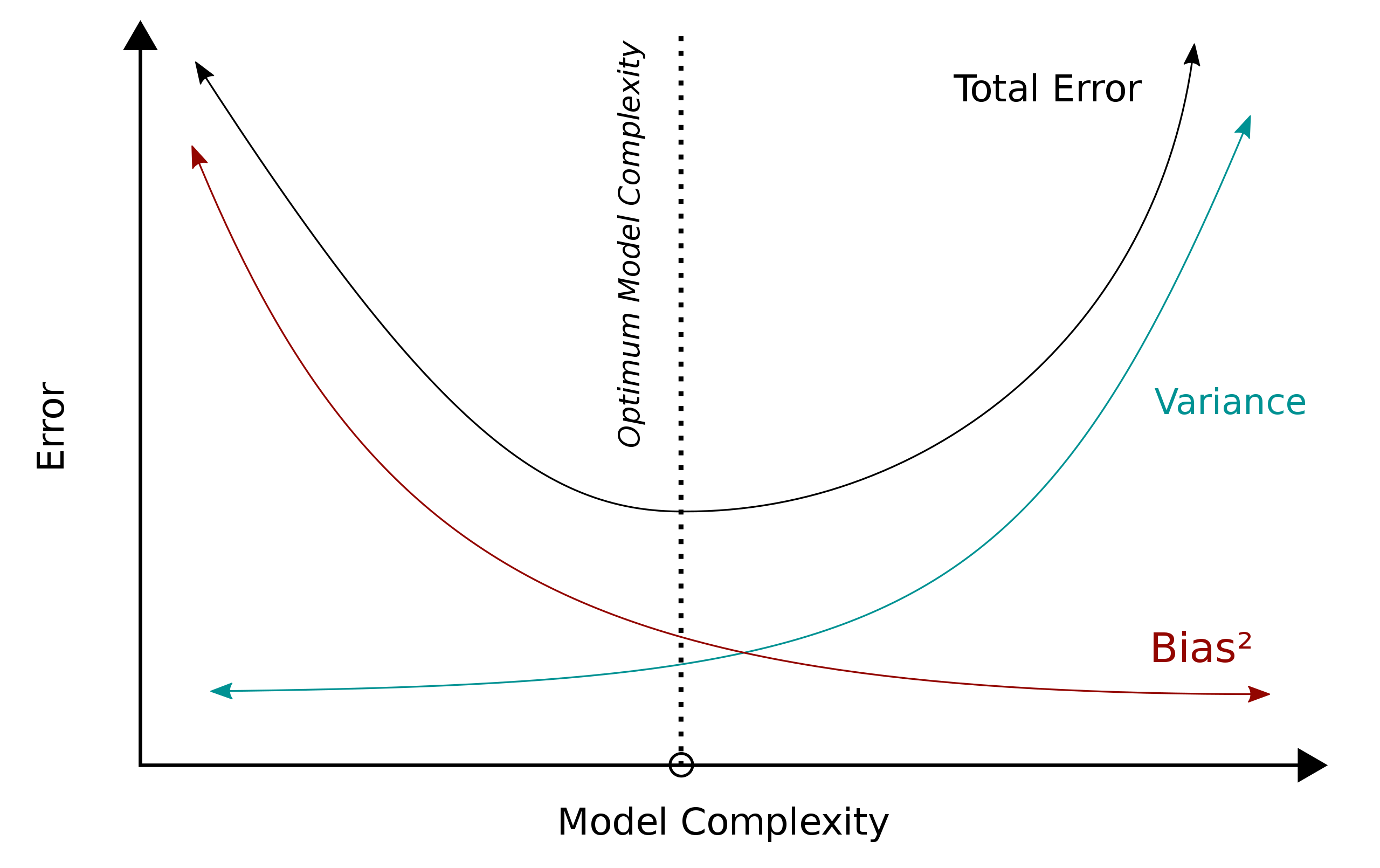
En la Figura 9.4 podemos ver gráficamente el dilema de bias-variance tradeoff. El sesgo generalmente se reduce aumentando la complejidad del modelo, por ejemplo, pasar de una modelo de regresión lineal a un modelo de regresión no lineal. Sin embargo, esto sobre-ajusta el modelo a los datos que se usaron para ajustarlo y por tanto si se usaran otros datos para ajustar el modelo, es posible que este cambie mucho y por tanto aumente la varianza. Lo ideal es encontrar un punto de equilibrio entre el sesgo y la varianza en el que se minimice el error total de predicción.
En la práctica es difícil descomponer el error de predicción total, pero se utilizan medidas que capturan tanto el sesgo como la varianza de los modelos. Veremos algunas de estas en las siguientes secciones.
9.2.1 Regresión
A la tarea de predecir una característica de naturaleza numérica se le conoce como regresión. La exactitud en esta tarea está dada por la diferencia entre la predicción y el valor real u observado. Mientras mayor sea la diferencia, menor es la exactitud, y viceversa. A esta diferencia se le conoce también como error de predicción, y puede estar representado de diferentes formas, las cuales veremos a continuación.
9.2.1.1 Error cuadrático medio
De ahora en adelante representaremos a la predicción como
El error cuadrático es la diferencia al cuadrado de la predicción y el valor real, es decir
Ajustaremos 2 modelos de regresión lineal usando la data fev para mostrar cómo calcular el MSE:
Podemos usar la función augment() del paquete broom para obtener los valores observados de la variable fev y los valores predichos de ambos modelos. Por ejemplo, para fit_1:
augment(fit_1)augment(fit_1) %>% DT::datatable(
options = list(display = "compact", pageLength = 5, scrollX = TRUE)
)Obtenemos los valores predichos y los valores observados de los dos modelos y los unimos:
Ahora agrupamos por modelo ajustado y calculamos el MSE:
# A tibble: 2 × 2
fit mse
<chr> <dbl>
1 fit_1 0.175
2 fit_2 0.156En este caso, el MSE tiene unidades en L^2. Según los resultados, vemos que el segundo modelo tiene mayor exactitud de predicción ya que su MSE es menor.
9.2.1.2 Raíz cuadrada del error cuadrático medio
La desventaja del MSE es que las unidades del error están al cuadrado. Por esta razón, se acostumbra usar la raíz cuadrada del error cuadrático medio o root mean square error (RMSE), la cual se define como
El paquete yardstick, parte de la colección tidymodels, tiene la función rmse() para calcular esta métrica. Veamos cómo usarla en el ejemplo anterior de los modelos de regresión lineal:
# A tibble: 2 × 4
fit .metric .estimator .estimate
<chr> <chr> <chr> <dbl>
1 fit_1 rmse standard 0.419
2 fit_2 rmse standard 0.395El valor del RMSE lo vemos en la columna .estimate. Vemos que usando esta medida el segundo modelo tiene mayor exactitud de predicción. La diferencia es que ahora las unidades del RMSE están en
9.2.1.3 Error absoluto medio
Otra forma de expresar el error de predicción es mediante el error absoluto, el cual es el valor absoluto de la diferencia entre el valor predicho y el valor observado, es decir,
Para comparar las predicciones de los modelos usando el MAE vamos a utilizar la función mae() del paquete yardstick.
# A tibble: 2 × 4
fit .metric .estimator .estimate
<chr> <chr> <chr> <dbl>
1 fit_1 mae standard 0.319
2 fit_2 mae standard 0.297Al igual que en el cálculo del RMSE, el MAE está en unidades de L. Utilizando esta última, se llega a la misma conclusión de que el segundo modelo es más exacto. Los valores del MAE generalmente son menores al RMSE, ya que el MAE no es tan sensible a las desviaciones o errores grandes como el RMSE. Por esta razón, el MAE es una medida más conservadora.
9.2.1.4 Error absoluto porcentual medio
La última forma que veremos para representar el error es el error absoluto relativo, el cual es la razón de la magnitud del error y la magnitud del valor real, es decir,
De igual manera, podemos usar la función mape() de yardstick para comparar las predicciones de los modelos:
# A tibble: 2 × 4
fit .metric .estimator .estimate
<chr> <chr> <chr> <dbl>
1 fit_1 mape standard 12.7
2 fit_2 mape standard 11.7La ventaja del MAPE es que es bastante intuitivo. Por ejemplo, el valor del MAPE para el primer modelo nos dice que, en promedio, la magnitud del error de predicción es el 12.7% de los valores observados. Sin embargo, el MAPE suele presentar problemas en la práctica. Uno de ellos es que si los valores observados son muy pequeños y cercanos a cero, entonces el cálculo del MAPE puede ser numéricamente inestable o imposible si es que se divide entre cero.
9.2.1.5 Múltiples medidas
Podemos definir un conjunto de medidas de exactitud usando la función metric_set() del paquete yardstick:
metrics_regression <- metric_set(rmse, mae, mape)
fit_predicted %>%
group_by(fit) %>%
metrics_regression(truth = obs, estimate = pred)# A tibble: 6 × 4
fit .metric .estimator .estimate
<chr> <chr> <chr> <dbl>
1 fit_1 rmse standard 0.419
2 fit_2 rmse standard 0.395
3 fit_1 mae standard 0.319
4 fit_2 mae standard 0.297
5 fit_1 mape standard 12.7
6 fit_2 mape standard 11.7 9.2.2 Clasificación
La tarea de clasificación consiste en usar una herramienta para darle una etiqueta a un individuo. Las pruebas de diagnóstico son un buen ejemplo de clasificación, ya que permiten saber si una persona posee o no una enfermedad. En este caso, las etiquetas podrían ser “Positivo” o “Negativo” a la presencia de un virus, por ejemplo. Las nociones previas de exactitud y precisión en mediciones numéricas no son directamente aplicables en clasificación. Es necesario volver a definirlas en este contexto. Además, veremos que no son las únicas medidas de qué tan buena o no es nuestra regla de clasificación, ya sea mediante un modelo estadístico o una prueba de diagnóstico.
A partir de esta sección, hablaremos de las métricas de evaluación de una herramienta de clasificación en el contexto de pruebas de diagnóstico. Para esto, usaremos el conjunto de datos ilustrativo diagnostico.csv, donde encontraremos los resultados simulados de dos pruebas diferentes para la detección de la presencia de un virus.
Veamos la data:
diagnosticos <- read_csv("data/diagnosticos.csv")Rows: 200 Columns: 3
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (2): diagnostico, real
dbl (1): prueba
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.View(diagnosticos)A continuación veremos diferentes medidas para evaluar el diagnóstico de las pruebas teniendo como referencia la condición real de cada individuo.
9.2.2.1 Matriz de confusión
La matriz de confusión consiste en la tabulación cruzada de las clases predichas y las clases reales. En el caso de pruebas de diagnóstico, consiste en tabular el diagnóstico de la prueba vs. la condición real de los individuos. La forma general de una matriz de confusión para dos clases es la siguiente:
| Diagnóstico | Positivo (P) | Negativo (N) |
|---|---|---|
| Positivo (PP) | Verdaderos Positivos (VP) |
Falsos Positivos (FP) |
| Negativo (PN) | Falsos Negativos (FN) |
Verdaderos Negativos (VN) |
Existen diferentes versiones según el ordenamiento de las filas y columnas de esta matriz. El orden no es importante, ya que las fórmulas de las métricas que se generan de la matriz de confusión no cambian por el orden.
La condición actual de los individuos puede ser negativa (N), si es que no tienen la condición, o positiva (P) si es que la tienen. Si, por otro lado, el diagnóstico es negativo, es decir, la prueba determina que el individuo no tiene la condición, entonces hablamos de un predictivo negativo (PN), mientras que si el diagnóstico es positivo, o sea, la prueba determina que el individuo sí tiene la condición, entonces hablamos de un predictivo positivo (PP).
Sea cual fuese la variación, la diagonal siempre va a contener a la cantidad de individuos correctamente diagnosticados. Según la presencia o la ausencia de la condición estudiada en los individuos, se definen las siguientes cantidades:
Verdaderos negativos (VN): Cantidad de individuos sin la condición para los cuales la prueba de diagnóstico determinó correctamente que no tenían la condición.
Verdaderos positivos (VP): Cantidad de individuos con la condición para los cuales la prueba de diagnóstico determinó correctamente que sí tenían la condición.
Por otro lado, los errores de diagnóstico estarían fuera de la diagonal, definiéndose así las siguientes cantidades:
Falsos Negativos (FN): Cantidad de individuos con la condición para los cuales la prueba de diagnóstico determinó incorrectamente que no tenían la condición.
Falsos Positivos (FP): Cantidad de individuos sin la condición para los cuales la prueba de diagnóstico determinó incorrectamente que sí tenían la condición.
Veamos como ejemplo la matriz de confusión de los diagnósticos de la primera prueba. Antes, convertiremos las variables diagnostico y real en factores.
El orden de los niveles en el argumento levels es importante ya que las funciones que veremos en este capítulo definen a uno de los niveles como el evento de interés; es decir, el evento o la clase para la cual queremos evaluar qué tan bien predicen las herramientas de clasificación o diagnóstico. En este caso, podríamos definir al nivel “Positivo” como la clase de interés, ya que es más importante que las pruebas de diagnóstico puedan clasificar correctamente a las personas que tengan la enfermedad que a las que no tienen. El evento de interés va a depender mucho del objetivo del estudio o aplicación. Los paquetes que veremos en este capítulo son yardstick y pubh. El paquete yardstick toma como evento de interés al primer nivel, mientras que el paquete pubh al segundo nivel. Por ahora, dejaremos a nuestro evento de interés “Positivo” como el primer nivel. Cuando usemos el paquete pubh, veremos una forma para revertir el orden.
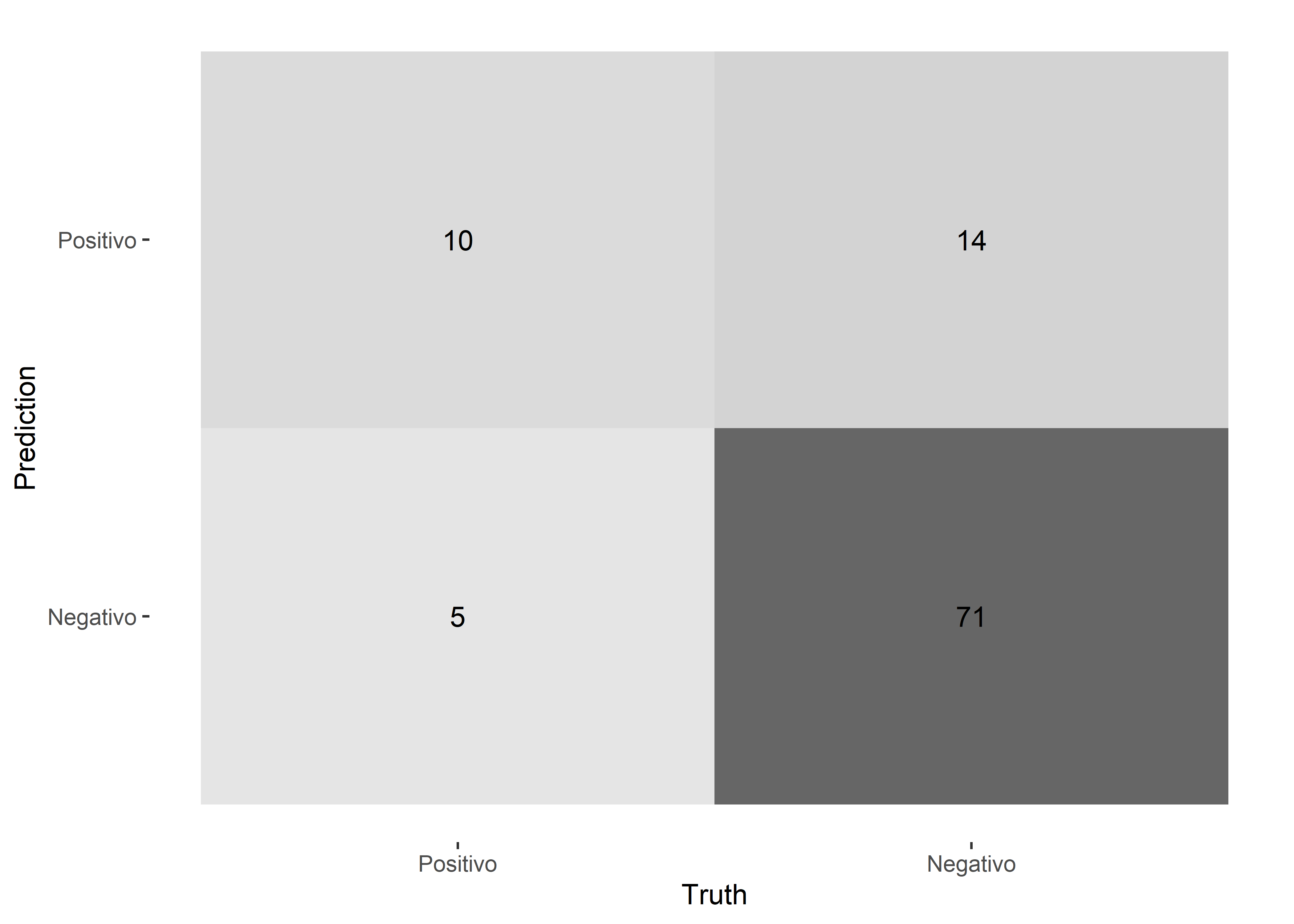
Filtraremos los resultados de la primera prueba y mediante la función conf_mat() del paquete yardstick mostraremos la matriz de confusión:
Truth
Prediction Positivo Negativo
Positivo 10 14
Negativo 5 71Para visualizar la matriz de confusión, podemos utilizar un heatmap. Este gráfico puede generarse con la función autoplot() del paquete ggplot2.
Veamos ahora las métricas de evaluación de diagnóstico más importantes que se pueden generar de la matriz de confusión.
9.2.2.2 Exactitud
La exactitud (Ecuación 9.15) en el caso de clasificación tiene una definición diferente a la evaluación de mediciones numéricas. En este caso, la exactitud se define como el número de diagnósticos correctos entre el total de individuos.
Para calcular la exactitud usamos la función accuracy() del paquete yardstick. Comparemos la exactitud de las pruebas de diagnóstico:
# A tibble: 2 × 4
prueba .metric .estimator .estimate
<dbl> <chr> <chr> <dbl>
1 1 accuracy binary 0.81
2 2 accuracy binary 0.78La columna .metric indica la métrica utilizada y el la columna .estimate su valor. En este caso, podemos ver que la primera prueba tiene mayor exactitud que la segunda.
9.2.2.3 Sensibilidad
La sensibilidad (Ecuación 9.16) o tasa de verdaderos positivos se refiere a la probabilidad de una prueba positiva dado que la condición también es positiva.
Para calcular la sensibilidad usamos la función sens().
# A tibble: 2 × 4
prueba .metric .estimator .estimate
<dbl> <chr> <chr> <dbl>
1 1 sens binary 0.417
2 2 sens binary 0.833En términos de sensibilidad, la segunda prueba es superior a la primera.
9.2.2.4 Especificidad
La especificidad (Ecuación 9.17) o tasa de verdaderos negativos se refiere a la probabilidad de una prueba negativa dado que la condición también es negativa.
Para calcular la especificidad usamos la función spec().
# A tibble: 2 × 4
prueba .metric .estimator .estimate
<dbl> <chr> <chr> <dbl>
1 1 spec binary 0.934
2 2 spec binary 0.763Vemos que, en términos de especifidad, la primera prueba es superior.
9.2.2.5 Precisión
La precisión (Ecuación 9.18) o valor predictivo positivo es la proporción de pruebas positivas que diagnosticaron correctamente una condición positiva.
Para calcular la precisión usamos la función precision().
# A tibble: 2 × 4
prueba .metric .estimator .estimate
<dbl> <chr> <chr> <dbl>
1 1 precision binary 0.667
2 2 precision binary 0.526La primera prueba es superior a la segunda en términos de precisión.
También se puede usar la función ppv() que calcula el valor predictivo positivo.
9.2.2.6 Valor predictivo negativo
El valor predictivo negativo (Ecuación 9.19) es la proporción de pruebas negativas que detectaron correctamente una condición negativa.
Para calcular el valor predictivo negativo usamos la función npv().
# A tibble: 2 × 4
prueba .metric .estimator .estimate
<dbl> <chr> <chr> <dbl>
1 1 npv binary 0.835
2 2 npv binary 0.935En este caso, la segunda prueba es superior.
9.2.2.7 Coeficiente de correlación de Matthews
El coeficiente de correlación de Matthews (MCC) o coeficiente phi es una medida de asociación entre dos variables categóricas, en este caso, entre el diagnóstico y la condición real. Dos variables categóricas van a estar más asociadas si la mayoría de casos cae dentro de la diagonal de la matríz de confusión, mientras que una menor asociación correspondería a si la mayoría de casos caen fuera de la diagonal.
Para calcular el MCC usamos la función mcc().
# A tibble: 2 × 4
prueba .metric .estimator .estimate
<dbl> <chr> <chr> <dbl>
1 1 mcc binary 0.420
2 2 mcc binary 0.525Según el MCC, la segunda prueba es superior.
9.2.2.8 Coeficiente kappa
El coeficiente kappa mide la concordancia entre las clases de dos variables categóricas, en este caso, entre el diagnóstico y la condición real. El coeficiente kappa no solo toma en cuenta la concordoncia observada, sino también la posibilidad de que la concordancia ocurra por azar.
Para calcular el coeficiente kappa usamos la función kappa().
# A tibble: 2 × 4
prueba .metric .estimator .estimate
<dbl> <chr> <chr> <dbl>
1 1 kap binary 0.403
2 2 kap binary 0.497La segunda prueba es superior según el coeficiente kappa.
9.2.2.9 Múltiples medidas
Al igual que en el caso de regresión, podemos definir un conjunto de medidas de exactitud usando la función metric_set() del paquete yardstick:
metrics_classification <- metric_set(accuracy, sens, spec)
diagnosticos %>%
group_by(prueba) %>%
metrics_classification(truth = real, estimate = diagnostico)# A tibble: 6 × 4
prueba .metric .estimator .estimate
<dbl> <chr> <chr> <dbl>
1 1 accuracy binary 0.81
2 2 accuracy binary 0.78
3 1 sens binary 0.417
4 2 sens binary 0.833
5 1 spec binary 0.934
6 2 spec binary 0.763Por último, también podemos obtener múltiples métricas de clasificación y sus intervalos de confianza con la función diag_test() del paquete pubh. Para usar esta función es necesario cambiar el orden de los niveles, ya que esta considera como el evento de interés al segundo nivel. Para revertir el orden de los niveles podemos usar la función fct_rev() del paquete forcats que se encuentra dentro del tidyverse:
Para la prueba 1:
Outcome + Outcome - Total
Test + 10 5 15
Test - 14 71 85
Total 24 76 100
Point estimates and 95% CIs:
--------------------------------------------------------------
Apparent prevalence * 0.15 (0.09, 0.24)
True prevalence * 0.24 (0.16, 0.34)
Sensitivity * 0.42 (0.22, 0.63)
Specificity * 0.93 (0.85, 0.98)
Positive predictive value * 0.67 (0.38, 0.88)
Negative predictive value * 0.84 (0.74, 0.91)
Positive likelihood ratio 6.33 (2.40, 16.72)
Negative likelihood ratio 0.62 (0.44, 0.88)
False T+ proportion for true D- * 0.07 (0.02, 0.15)
False T- proportion for true D+ * 0.58 (0.37, 0.78)
False T+ proportion for T+ * 0.33 (0.12, 0.62)
False T- proportion for T- * 0.16 (0.09, 0.26)
Correctly classified proportion * 0.81 (0.72, 0.88)
--------------------------------------------------------------
* Exact CIsPara la prueba 2:
Outcome + Outcome - Total
Test + 20 18 38
Test - 4 58 62
Total 24 76 100
Point estimates and 95% CIs:
--------------------------------------------------------------
Apparent prevalence * 0.38 (0.28, 0.48)
True prevalence * 0.24 (0.16, 0.34)
Sensitivity * 0.83 (0.63, 0.95)
Specificity * 0.76 (0.65, 0.85)
Positive predictive value * 0.53 (0.36, 0.69)
Negative predictive value * 0.94 (0.84, 0.98)
Positive likelihood ratio 3.52 (2.26, 5.47)
Negative likelihood ratio 0.22 (0.09, 0.54)
False T+ proportion for true D- * 0.24 (0.15, 0.35)
False T- proportion for true D+ * 0.17 (0.05, 0.37)
False T+ proportion for T+ * 0.47 (0.31, 0.64)
False T- proportion for T- * 0.06 (0.02, 0.16)
Correctly classified proportion * 0.78 (0.69, 0.86)
--------------------------------------------------------------
* Exact CIs9.3 Ejercicios
Ejercicio 1
El conjunto de datos “ChickWeight” contiene las observaciones de un experimento en el que se quizo evaluar el efecto de cuatro tipos de dieta en el crecimiento de pollitos. El conjunto de datos puede cargarse usando la siguiente línea de codigo:
data("ChickWeight")Este conjunto de datos tiene las siguientes variables:
-
weight: Peso del pollito en gramos. -
Time: Días desde el nacimiento cuando se hizo la medición. -
Chick: Identificador del pollito. -
Diet: Tipo de dieta que consumió el pollito.
Dado que hay más de una observación para cada pollito, calcular el promedio de las mediciones del peso de cada uno. Luego, estimar la media del peso promedio de los pollitos durante el experimento para cada tipo de dieta. Calcular el error estándar del estimador y los intervalos de confianza para la media. Graficar estas estimaciones usando las geometrías de gplot correspondientes y comparar la precisión de las estimaciones de cada grupo.
Ejercicio 2
Para este ejercicio se usará el conjunto de datos fev con el que se trabajó en la sección Sección 9.2.1. El objetivo es evaluar el error de predicción usando las medidas RMSE, MAE y MAPE de los siguientes modelos:
El modelo regre_model_3 es un tipo de modelo de regresión llamado modelo aditivo generalizado (GAM, por sus siglas en inglés). Este modelo es una generalización del modelo de regresión lineal ya que permite que los predictores tengan un efecto no lineal sobre la respuesta. Lo que se estima en un GAM no es un solo un coeficiente para cada predictor, sino una función no lineal del predictor. Este tipo de modelo se puede ajustar usando la función gam() del paquete mgcv. Las funciones s() en la formula sirven para especificar que queremos estimar una función no lineal del predictor. Se espera que estos modelos tengan un menor error de predicción que los modelos lineales, ya que en la práctica es difícil que un modelo lineal capture la verdadera asociación entre los predictores y la variable de respuesta. En cambio, un GAM es más flexible y puede capturar asociaciones relativamente complejas. Sin embargo, los GAM son generalmente son más difíciles de interpretar.
Para extraer los valores predichos de un GAM, se pueden usar las mimas funciones vistas para los modelos de regresión lineal. En general, la mayoría de funciones que trabajan sobre objetos creados por lm() se pueden usar sobre objetos creados con gam().
Ejercicio 3
El conjunto de datos “Bernard” del paquete pubh contiene las observaciones de un ensayo clínico aleatorizado para evaluar el efecto del ibuprofeno intravenoso en 455 pacientes con sepsis. El conjunto de datos puede cargarse usando la siguiente línea de codigo:
data("Bernard", package = "pubh")Este conjunto de datos tiene las siguientes variables:
-
id: Identificador del paciente. -
treat: Tratamiento con niveles “Placebo” y “Ibuprofen”. -
race: Raza/etnicidad con niveles “White”, “African American” y “Other”. -
fate: Estado luego de 30 días con niveles “Alive” y “Dead”. -
apache: Puntuación inicial de la escala de Apache. -
o2del: Oxígeno administrado al inicio del estudio. -
followup: Tiempo de seguimiento en horas. -
temp0: Temperatura en grados centígrados al inicio del estudio. -
temp10: Temperatura en grados centígrados luego de 36 horas.
Previo al análisis, se realizará el siguiente procesamiento de los datos:
El objetivo es evaluar la predicción del estado luego de 30 días de cada paciente de los siguientes modelos de regresión logística:
Los modelos de regresión logística son similares en estructura que los modelos de regresión lineal, pero lo que los diferencia es el tipo de variable que es la respuesta. Mientras que en los modelos de regresión lineal la respuesta es una variable continua, en los modelos de regresión logística la respuesta es una variable categórica binaria, que en este caso es fate. En R, para ajustar un modelo de regresión logística, se utiliza la función glm(). Hay que tener en cuenta que esta función toma como evento de interés al segundo nivel de la variable de respuesta. En este caso, el evento de interés sería si la persona vive; es decir, la clase “Alive” de la variable fate.
Para una introducción más completa a los modelos de regresión logístico, revisar Capítulo 14.
Ahora, se calcularán las predicciones para cada modelo:
class_model_pred_1 <- class_model_fit_1 %>%
augment(type.predict = "response") %>%
mutate(pred_class = ifelse(.fitted > 0.5, "Dead", "Alive")) %>%
select(obs = fate, pred = pred_class)
class_model_pred_2 <- class_model_fit_2 %>%
augment(type.predict = "response") %>%
mutate(pred_class = ifelse(.fitted > 0.5, "Dead", "Alive")) %>%
select(obs = fate, pred = pred_class)
class_model_pred_3 <- class_model_fit_3 %>%
augment(type.predict = "response") %>%
mutate(pred_class = ifelse(.fitted > 0.5, "Dead", "Alive")) %>%
select(obs = fate, pred = pred_class)Apartir de estas tablas, el procedimiento para calcular las medidas de evaluación de la predicción es muy similar a lo que se hizo en este capítulo para los modelos de regresión lineal. En cada tabla, se tiene la clase real en obs y la predicción en pred. Usar las medidas de exactitud, el coeficiente de correlación de Matthews, y el coeficiente kappa para evaluar la predicción de los modelos. Pista: Es necesario convertir la columna donde se encuentran las clases reales y las clases predichas en factores para que podamos usar las funciones del paquete yardstick. Recordar que las funciones de este paquete toman al primer nivel de la variable de respuesta como el evento de interés.