24 Análisis de series de tiempo
24.1 General
Los análisis de series de tiempo:
Se utilizan para pronosticar los datos futuros utilizando los datos históricos disponibles (de la misma variable de interés).
Evalúan la autocorrelación de las observaciones en el tiempo.
Permiten descomponer los patrones de las series de tiempo (i.e. tendencias, estacionalidad, periodicidad).
Tipicamente son denotadas de la siguiente forma :
- En general, para caracterizar correctamente una serie de tiempo los estadisticos tales como la media y Covarianza(y por lo tanto la varianza) de la serie son clave, puesto que reflejan la tendencia y aucorrelacion de una serie
24.1.1 Tendencia
La tendencia de una serie temporal se refiere a la dirección general o patrónen los datos a lo largo del intervalo de tiempo analizado. Asi representa el componente de la serie que muestra el desarrollo de la serie excluyendo variaciones a corto plazo debidos a factores como por ejemplo los cíclicos.
24.1.2 Autocorrelación
La autocorrelación (AC) representa el grado de similitud entre una serie de tiempo dada y una versión rezagada (lag) de sí misma en intervalos de tiempo sucesivos.
La AC ayuda a estudiar cómo se relaciona cada observación de una serie temporal con su pasado reciente. Los procesos con una mayor autocorrelación son más predecibles.
24.2 Terminología
Serie de tiempo: Una secuencia de datos de una variable ordenada cronologicamente en intervalos de tiempo generalmente igualmente espaciados .
Procesos estocásticos:
Estacionarios (Atributos constantes en el tiempo)
No estacionarios (Atributos no constantes en el tiempo)
Modelos básicos de series de tiempo:
Ruido blanco o White Noise (WN)
Paseo aleatorio o Random Walk (RW)
Autoregresivo o Auto-regressive (AR)
Media movil o Moving Average (MA)
24.3 Paquetes y data
Los paquetes y conjuntos de datos a ser utilizados en esta sección son:
Exploraremos las siguientes series de tiempo:
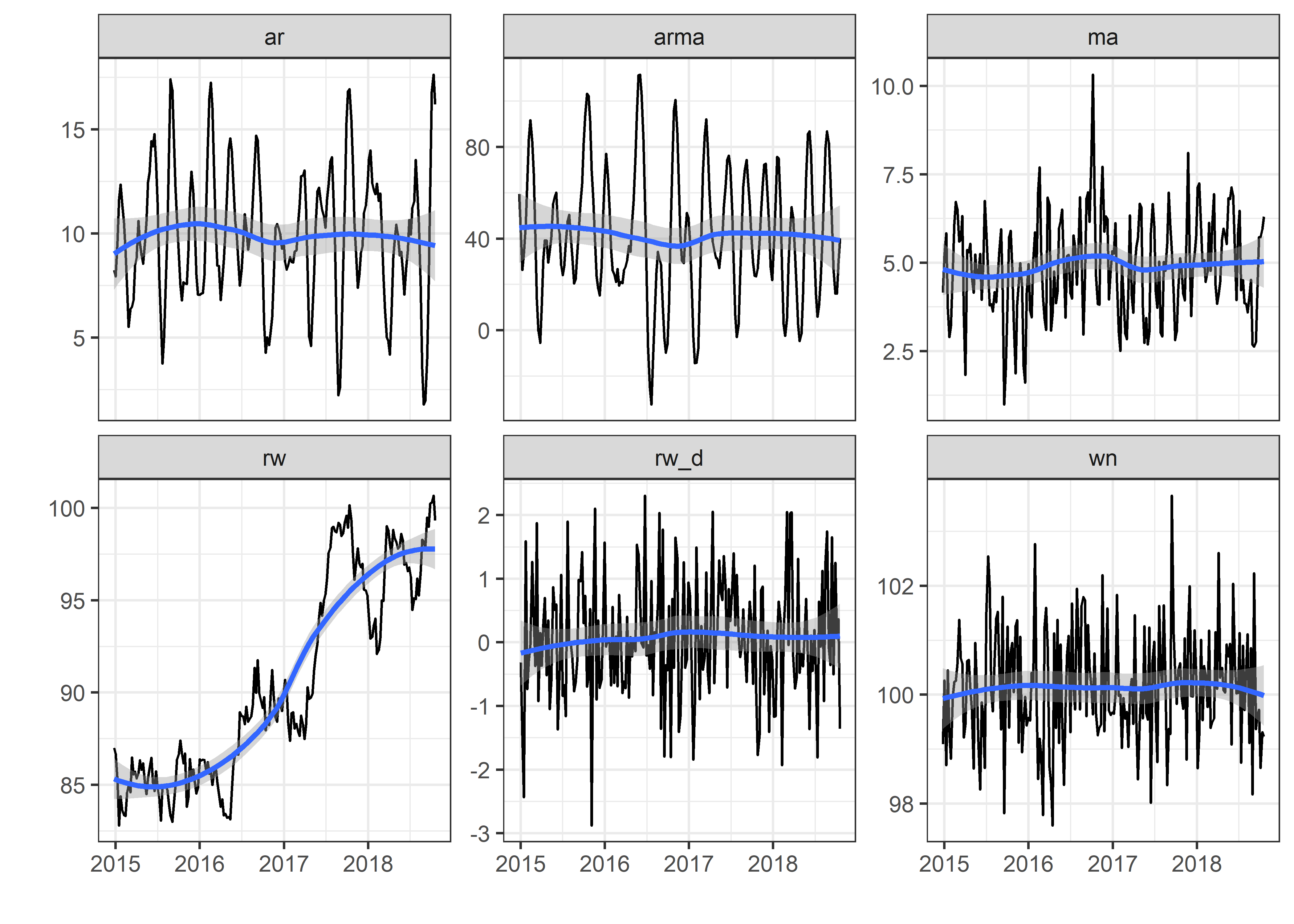
24.4 Procesos Estacionarios
24.4.1 Ruido blanco o White Noise (WN)
El ruido blanco es el ejemplo más simple de un proceso estocastico estacionario, el cual se caracteriza como ruido porque no tiene ningun patron, solo variacion aleatoria.
Un proceso de WN posee:
Una media fija y constante
Una varianza fija y constante
Ausencia correlación en el tiempo
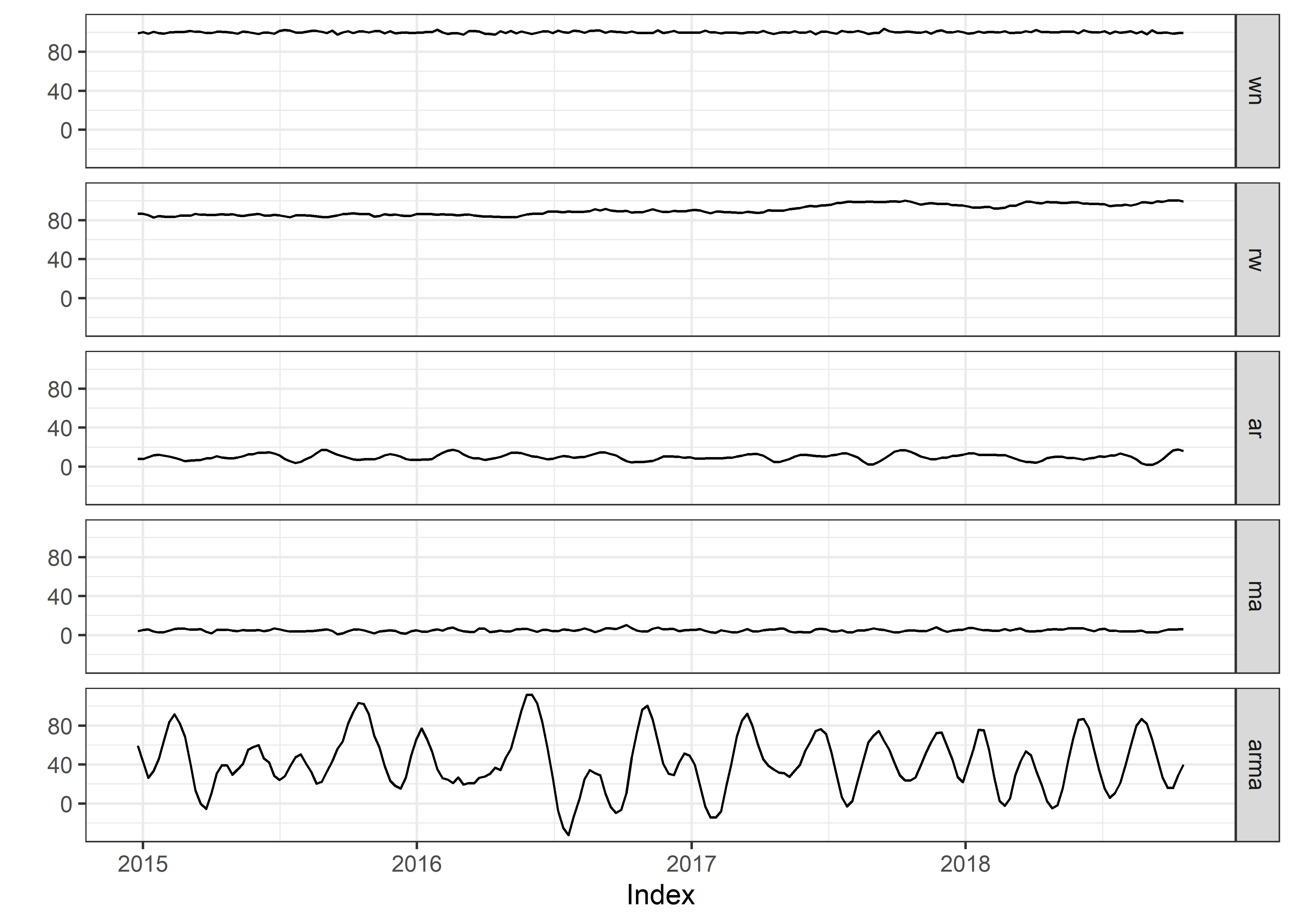
Por ejemplo, al revisar estas series de tiempo observamos:
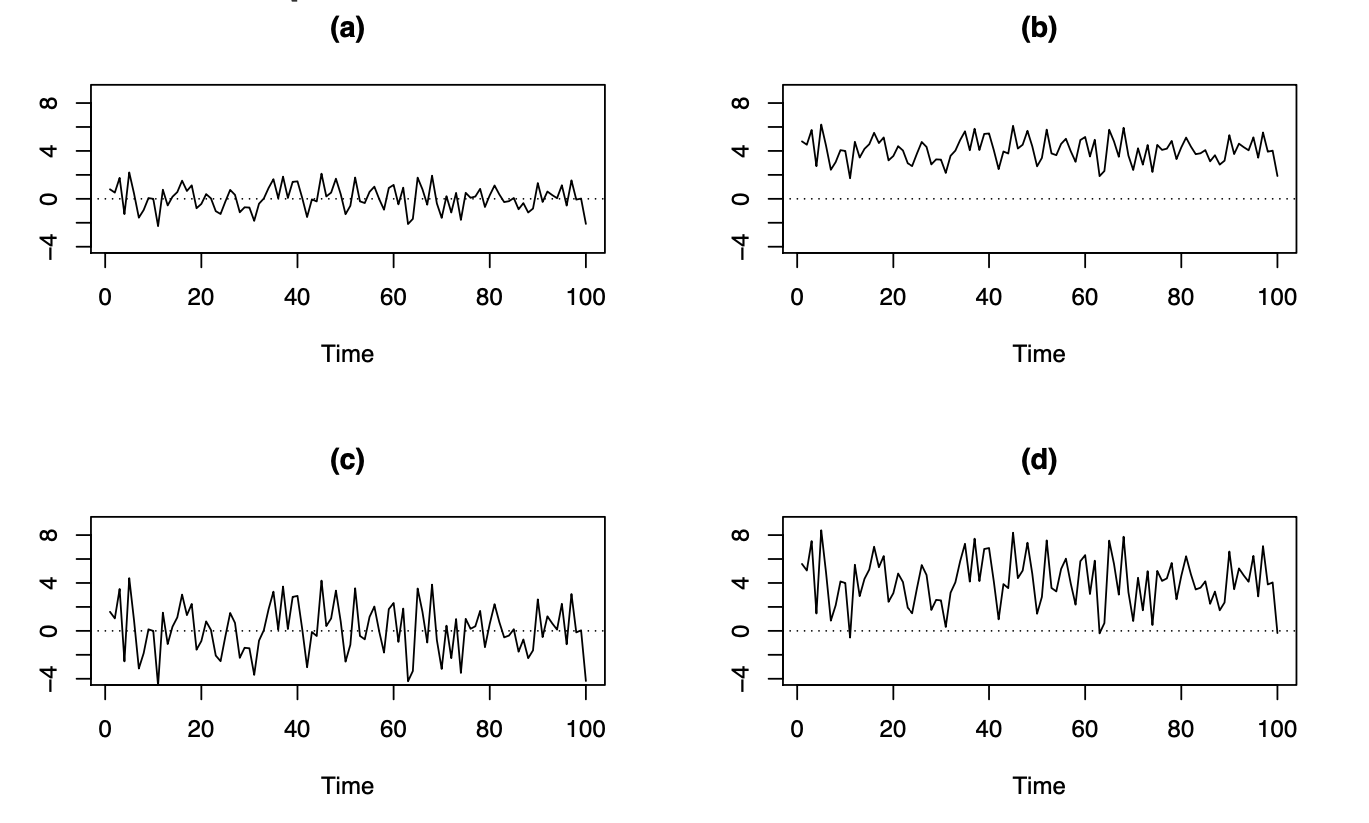
No hay patrón ni autocorrelación de los datos a lo largo del tiempo.
La serie se ha desplazado hacia arriba (media más grande), pero todavía no hay un patrón en los datos.
La serie tiene más variabilidad vertical (varianza más grande), aún sin patrón en los datos.
Media más grande y varianza más grande, todavía sin patrón en los datos.
Por otro lado, en estas series de tiempo observamos:
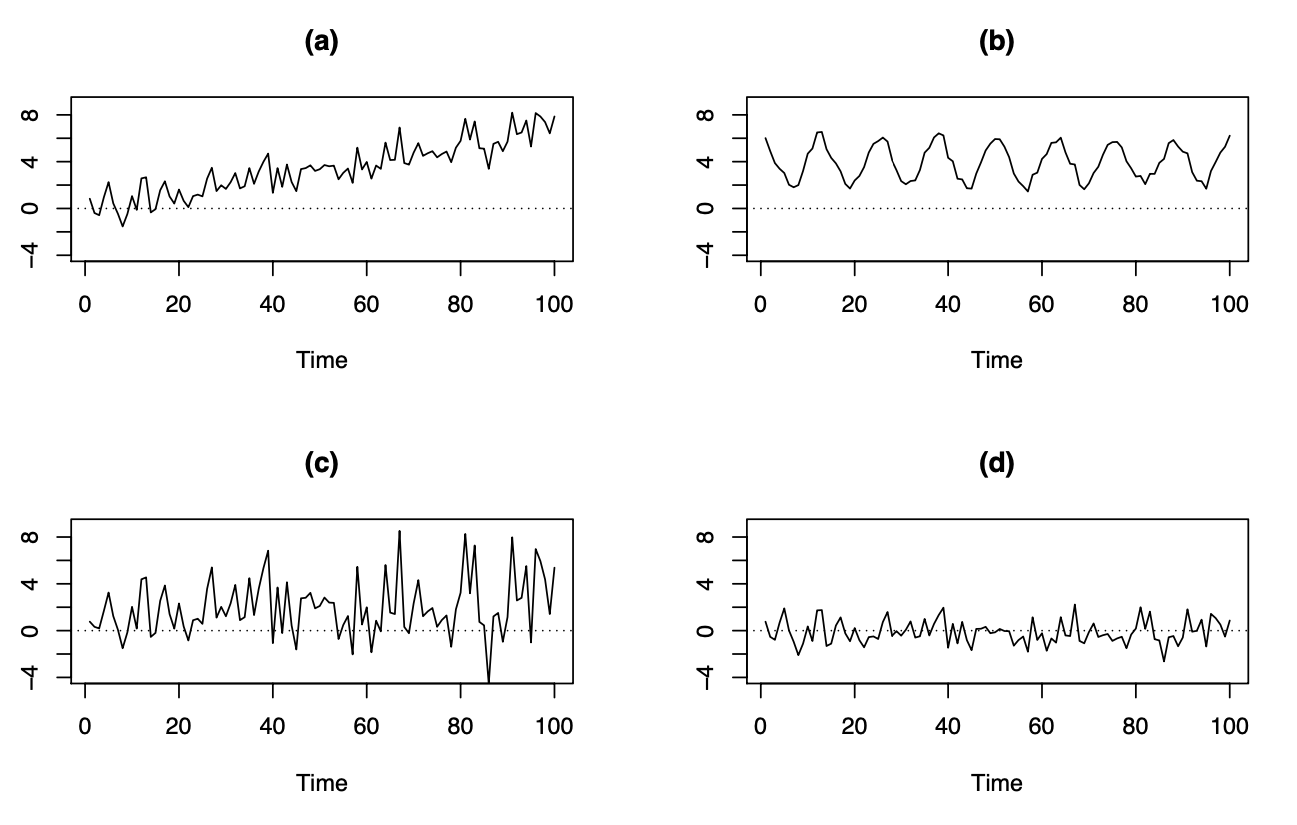
Tendencia creciente en el tiempo, media no constante en el tiempo.
Patrón periódico claro con duración de ciclo fijo (cada 12 observaciones), media no constante en el tiempo.
Mayor volatilidad(varianza) en el lado derecho que en el lado izquierdo. La varianza aumenta con el tiempo (la varianza es funcion del tiempo), no es constante.
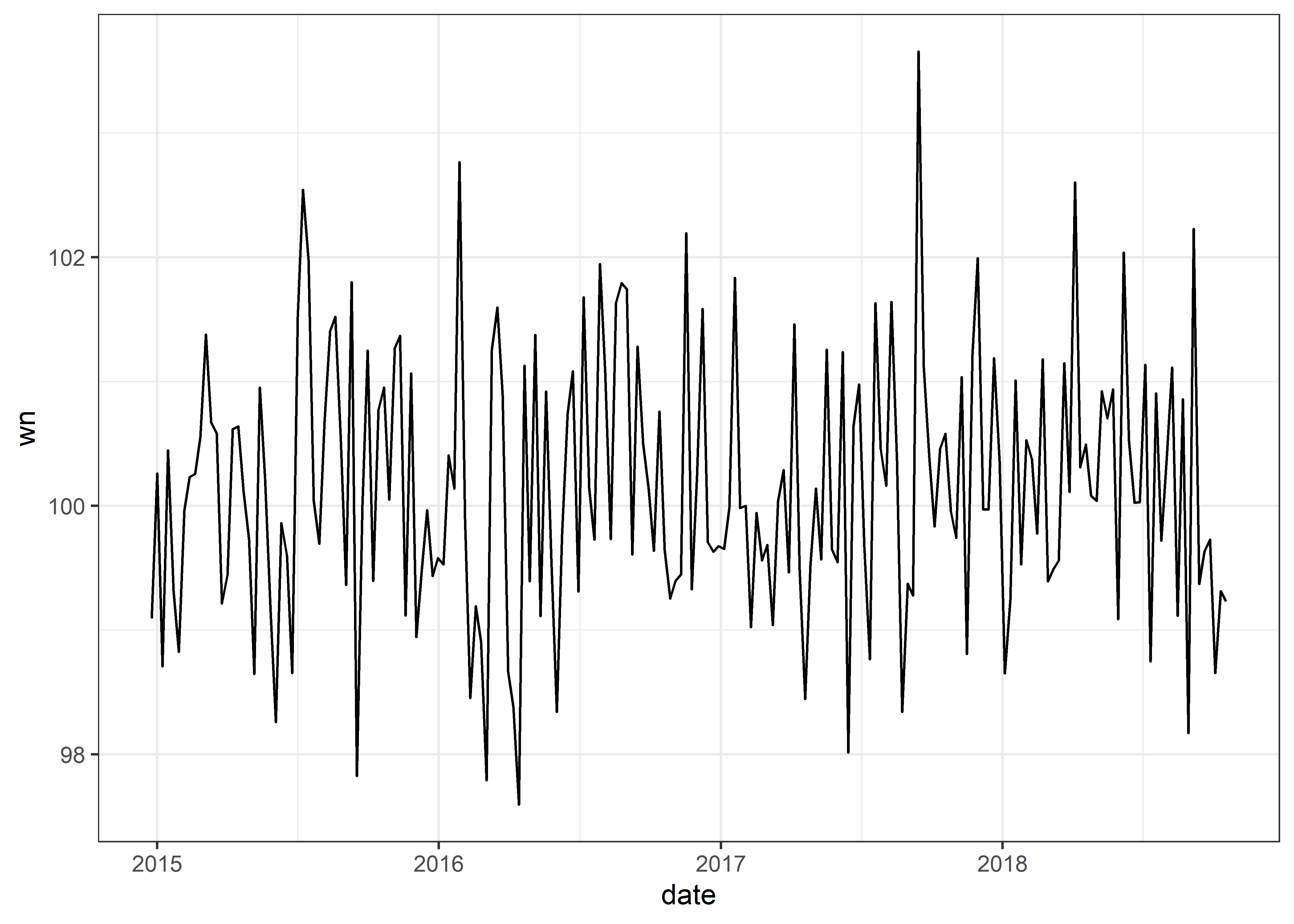
Media y varianza constantes, sin patrón en el tiempo (correlación). Esta serie de tiempo corresponde a un proceso de WN.
Graficaremos nuestra serie de tiempo wn
Podemos ajustar el formato de fechas usando scale_x_date y agregar una línea de tendencia usando geom_smooth.
dt_ts %>%
ggplot(aes(x = date, y = wn)) +
geom_line() +
scale_x_date(date_breaks = "4 months",
date_labels = "%d-%b") +
geom_smooth() +
theme_bw()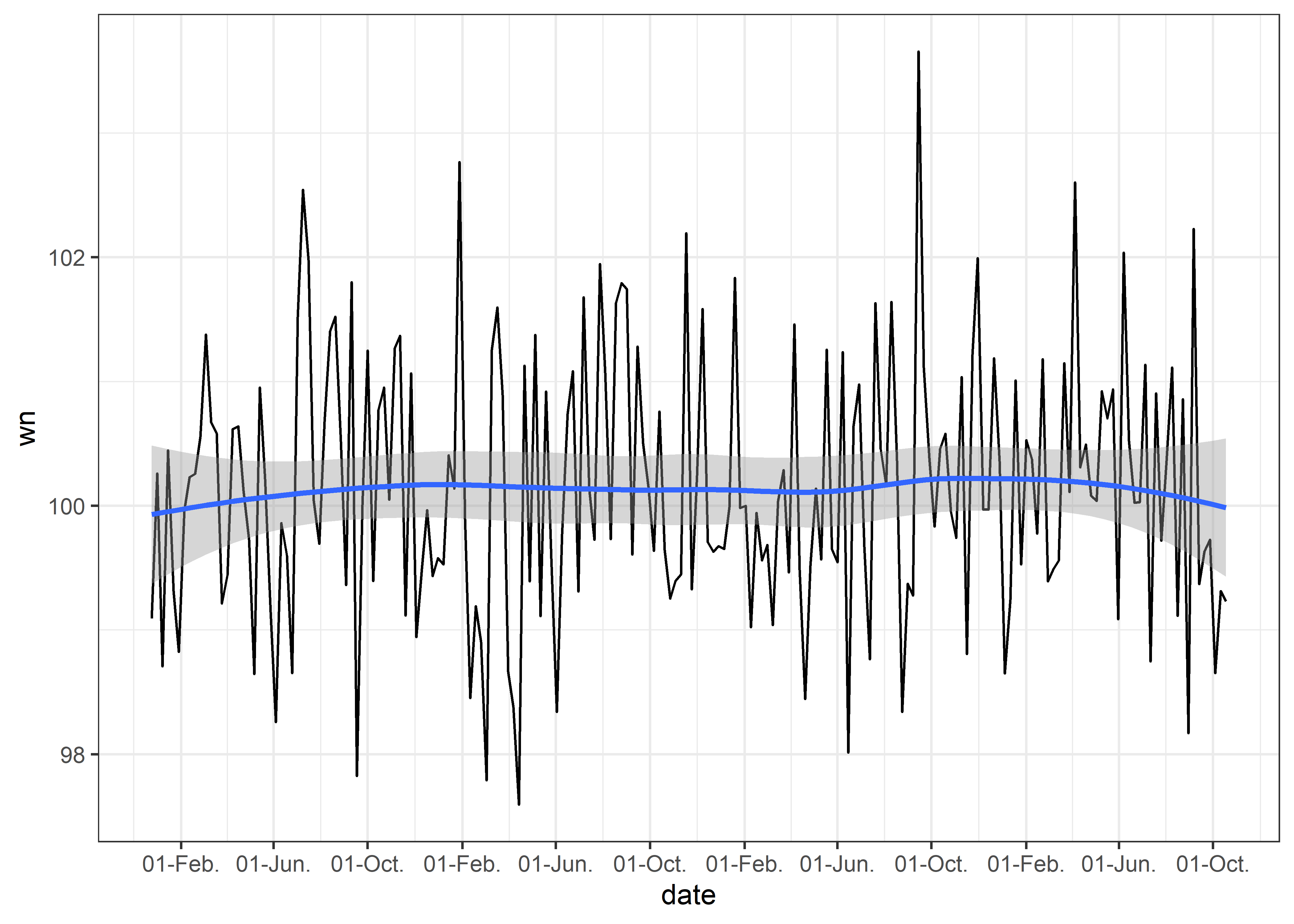
24.4.1.1 Formulación
Donde :
24.5 Procesos No Estacionarios
24.5.1 Paseo aleatorio o Random Walk (RW)
Un paseo aleatorio o Random Walk (RW) es el ejemplo más simple de un proceso no-estacionario.
Un proceso de RW:
- No tiene media ni varianza dependiente del tiempo (es constante a traves de toda la serie temporal).
- Tiene una fuerte dependencia en el tiempo.
- Sus cambios o incrementos son ruido blanco (WN).
En estas series de tiempo observamos:
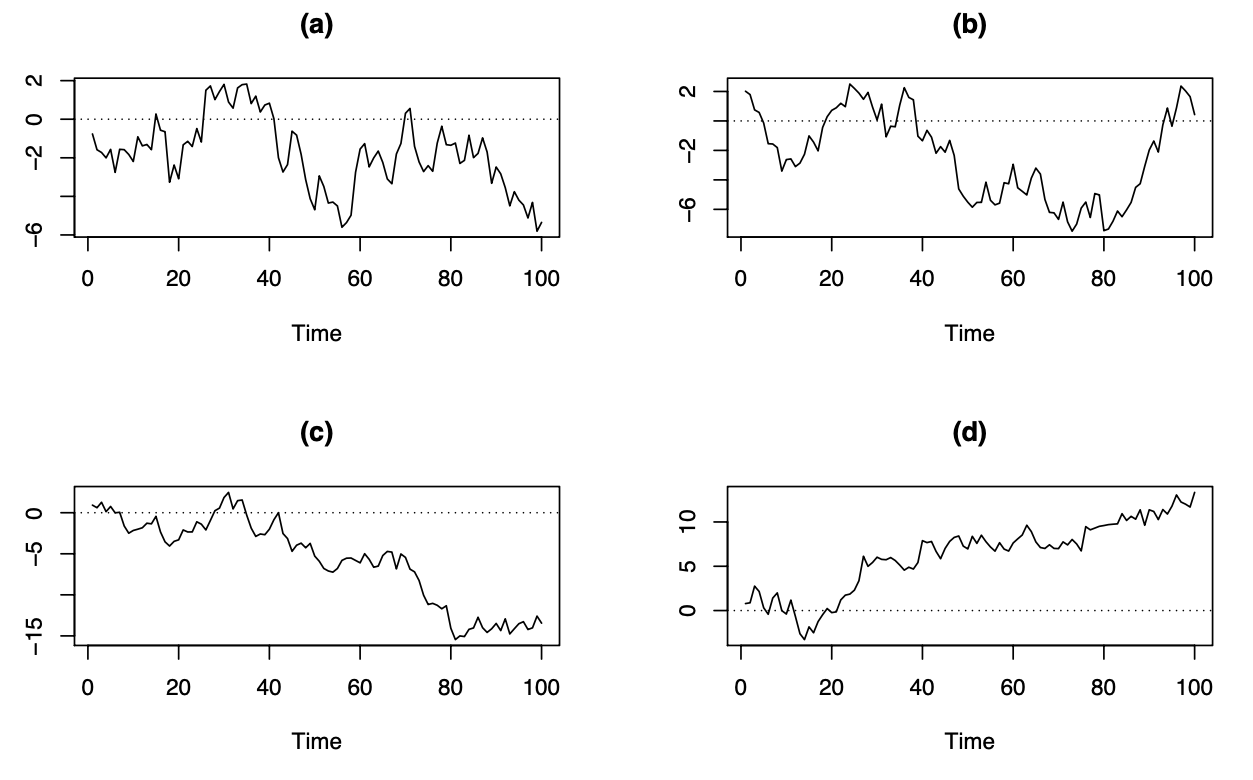
Las observaciones vecinas son similares. Las tendencias cortas al alza y a la baja parecen aleatorias.
Similar al caso A
Comienza en cero y tiene tendencia general a disminuir.
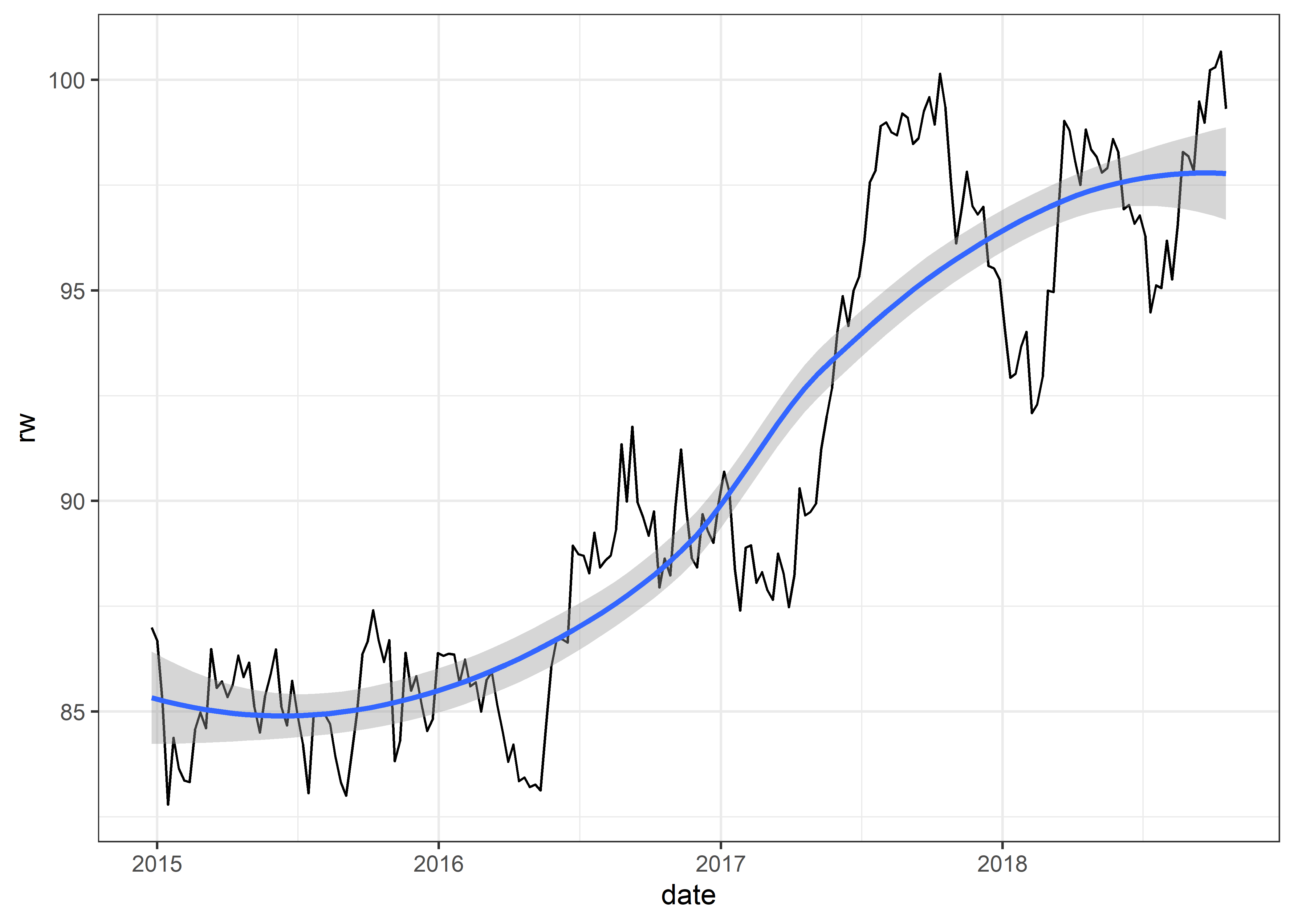
Comienza en cero y tiene tendencia general a aumentar.
Graficaremos nuestra serie de tiempo rw
24.5.1.1 Formulación
Aproximación WN
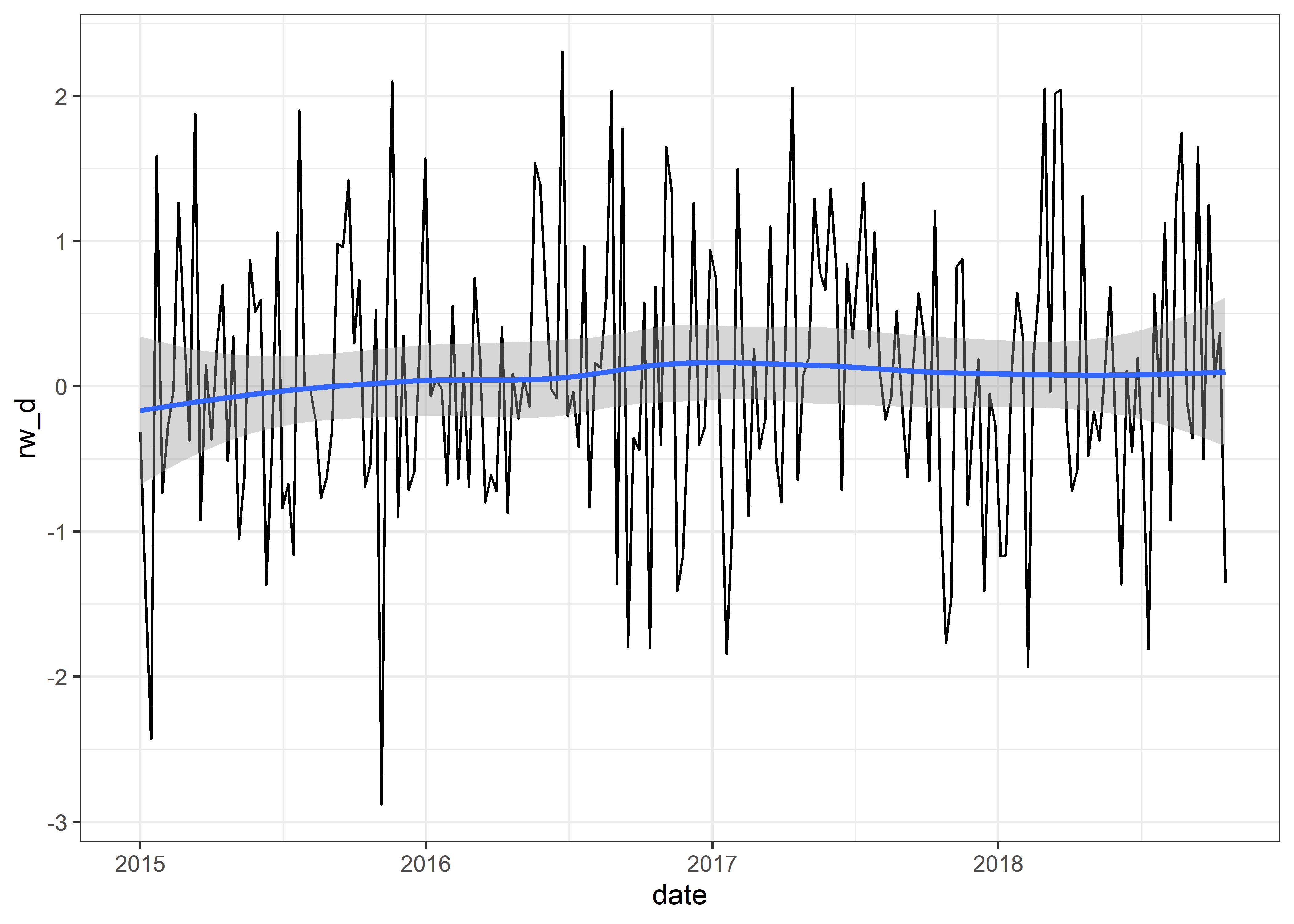
Por lo tanto, si hacemos la operación diff() (restar la observación actual con la observación anterior o tambien llamado rezago) nuestra serie temporal que tiene un patrón RW tendrá un patrón WN.
diff(RW)es un ejemplo de un proceso estacionario.
Para obtener parsimonia en un modelo de series de tiempo, a menudo se asume alguna forma de invariancia distribucional en el tiempo (o estacionariedad).
Los modelos estacionarios son parsimoniosos.
Los procesos estacionarios tienen estabilidad distribucional en el tiempo
¿Por qué? Un proceso estacionario se puede modelar con menos parámetros y muchos de los modelos de series temporales basan sus propiedades en diversos supuestos entre los cuales usualmente se encuentra el de estacionariedad.
Podemos calcular la diferenciación de nuestra serie de tiempo rw.
24.5.2 Modelo autorregresivo (AR)
El modelo autorregresivo representa una regresión o predicción del valor actual que se genera en función de los valores anteriores de esa misma serie temporal.
Dado que el valor actual se basa en los valores anteriores cercanos, el valor no cambia instantáneamente. Por ejemplo, la temperatura corporal no sube y baja rápidamente. Cambia constantemente y las medidas son cercanas entre sí.
24.5.2.1 Formulación
Aproximación WN
Si la pendiente es 0
Aproximación RW
Si la media es 0 y la pendiente
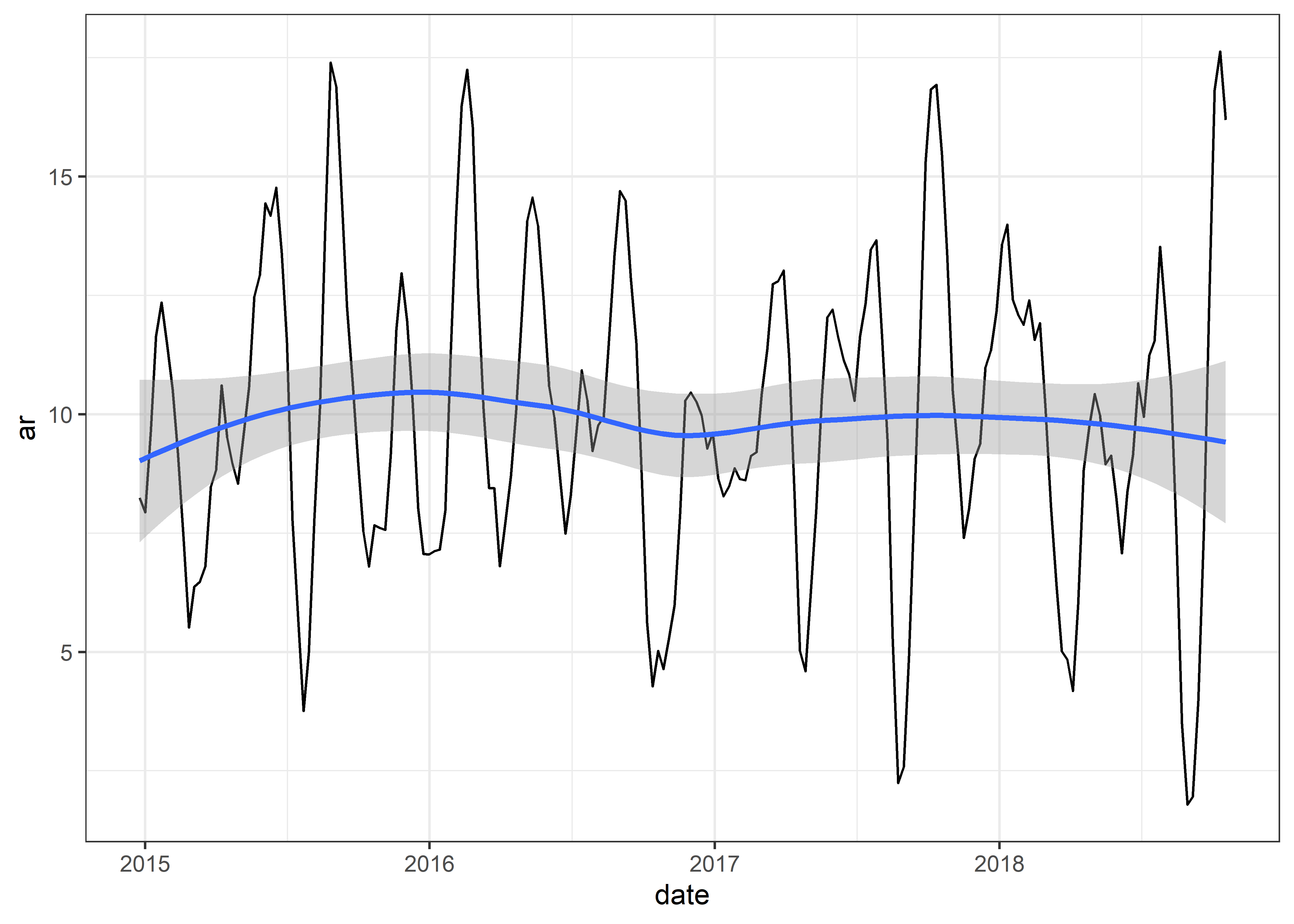
Graficaremos nuestra serie de tiempo ar
24.5.3 Modelo de media móvil (MA)
El modelo de media móvil genera los valores actuales en función de los errores de los pronósticos anteriores en lugar de utilizar los valores anteriores como AR. Los errores pasados se analizan para producir el valor actual.
24.5.3.1 Formulación
Aproximación WN
Si la pendiente es 0
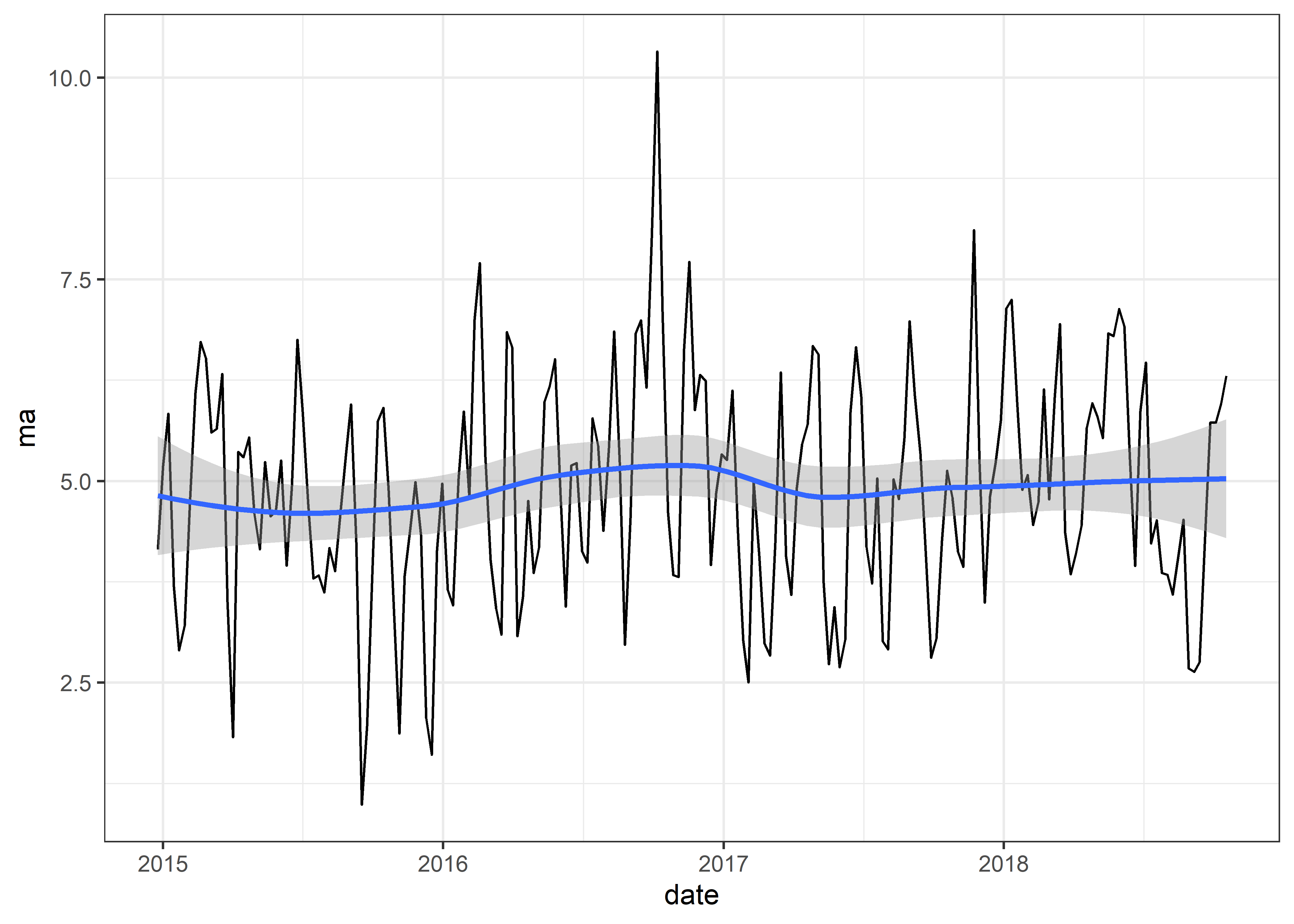
Graficaremos nuestra serie de tiempo ma
24.6 Modelos acoplados
24.6.1 Modelos ARMA
Es posible combinar las propiedades de los modelos AR y MA cuando la serie de tiempo es estacionaria.
El modelo ARMA predice los valores futuros basándose tanto en los valores anteriores como en los errores. Por lo tanto, ARMA suele tener un mejor rendimiento que los modelos AR y MA por separado.
24.6.1.1 Formulacion
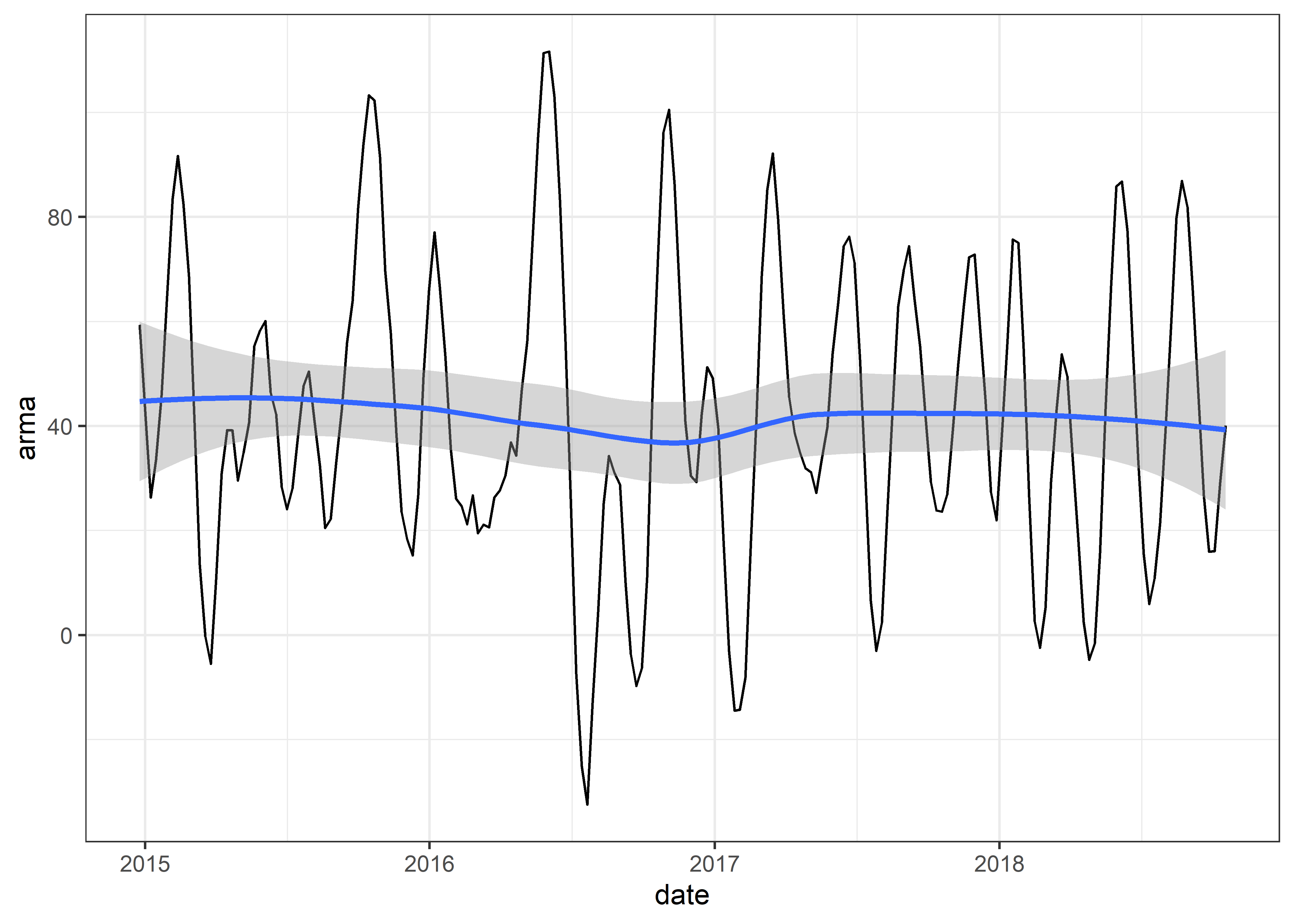
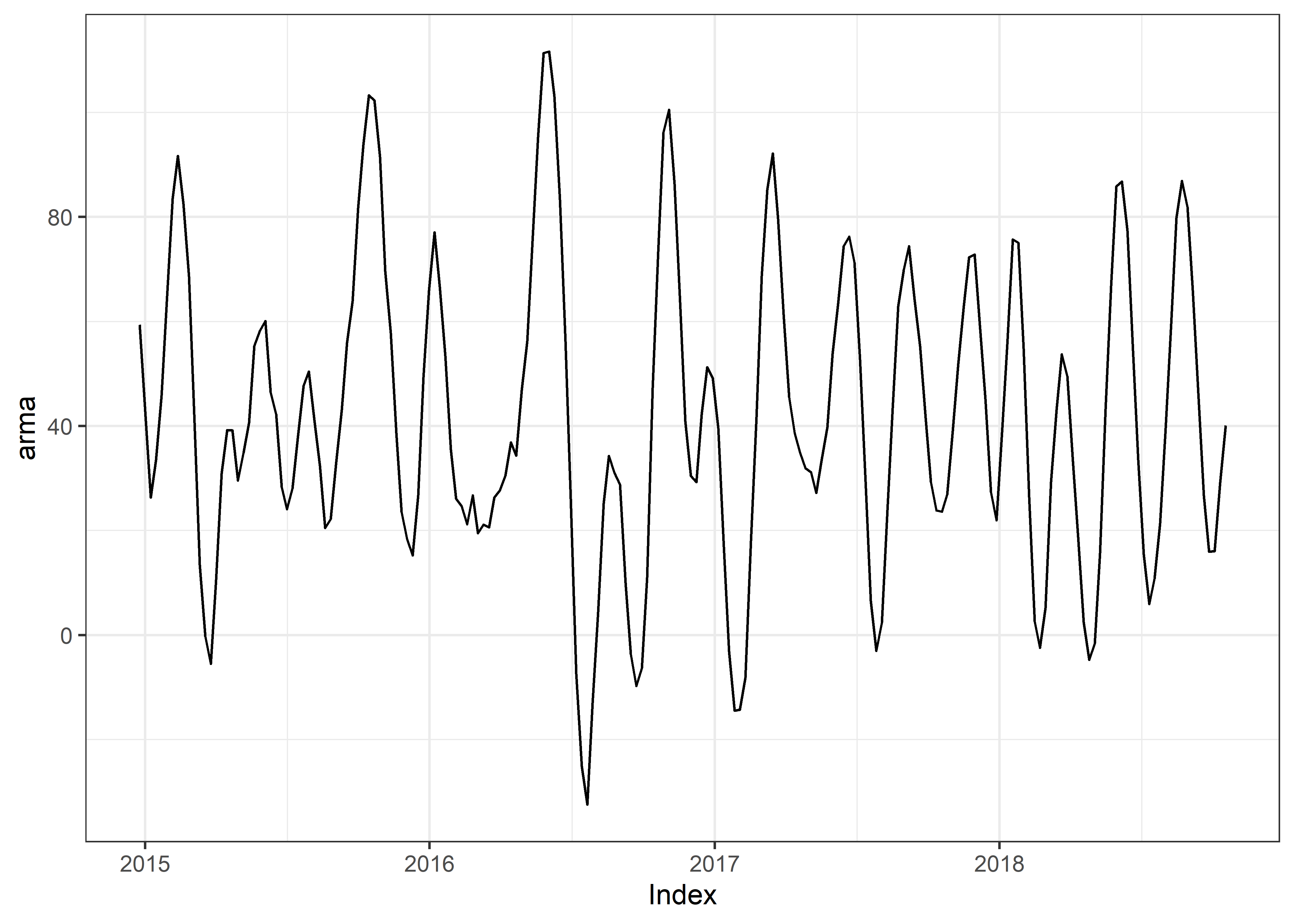
Graficaremos nuestra serie de tiempo arma
24.6.2 Función de autocorrelación (ACF)
Una de las formas de evaluación del mejor modelo para las series temporales es a través de sus funciones de autocorrelación.
La función de autocorrelación (ACF) es la correlación entre la observación actual y la observación en un rezago (lag) determinado.
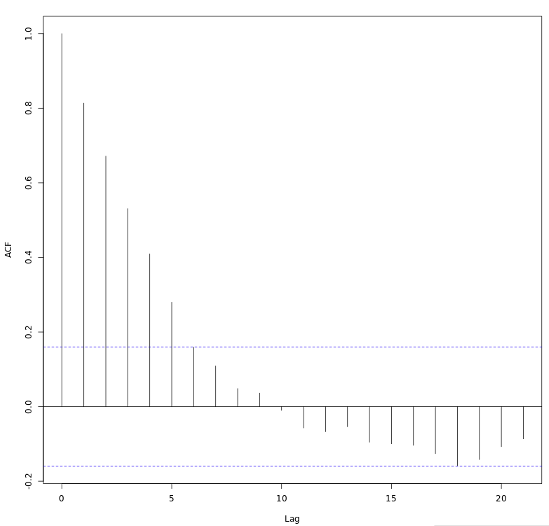
El ACF en lag-0 siempre es 1.
Cada figura de ACF incluye un par de líneas discontinuas horizontales azules que representan intervalos de confianza del 95 % de los rezagos (lag) centrados en cero.
Estos se utilizan para determinar la importancia estadística de una estimación de autocorrelación individual en un retraso dado frente a un valor nulo de cero.
Por ejemplo, en las siguientes series temporales observamos:
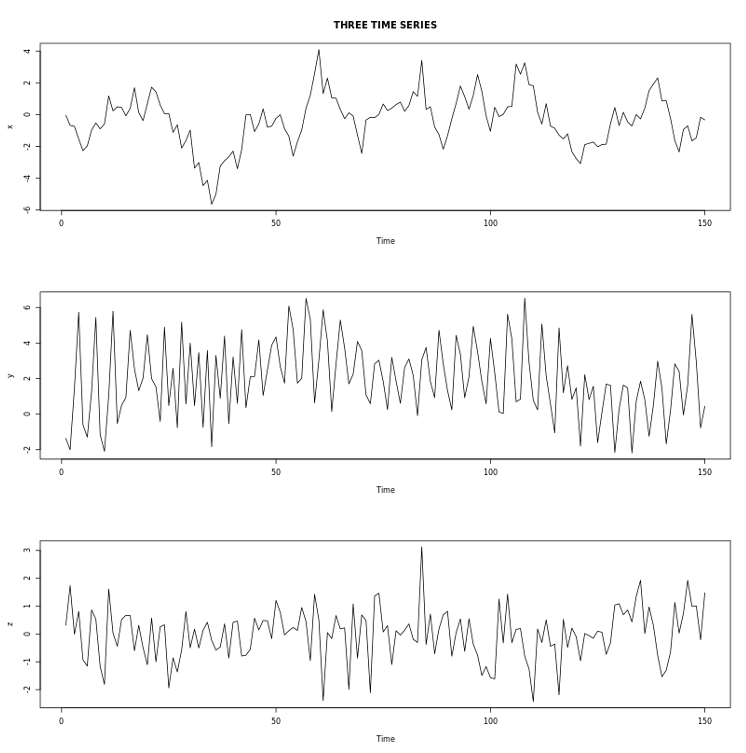
x) muestra una fuerte persistencia, lo que significa que el valor actual es muy cercano a los que lo preceden.
y) muestra un patrón periódico con una duración de ciclo de aproximadamente cuatro observaciones, lo que significa que el valor actual está relativamente cerca de la observación cuatro anterior.
z) no muestra ningún patrón claro.
Al explorar los ACF de las series temporales observamos:
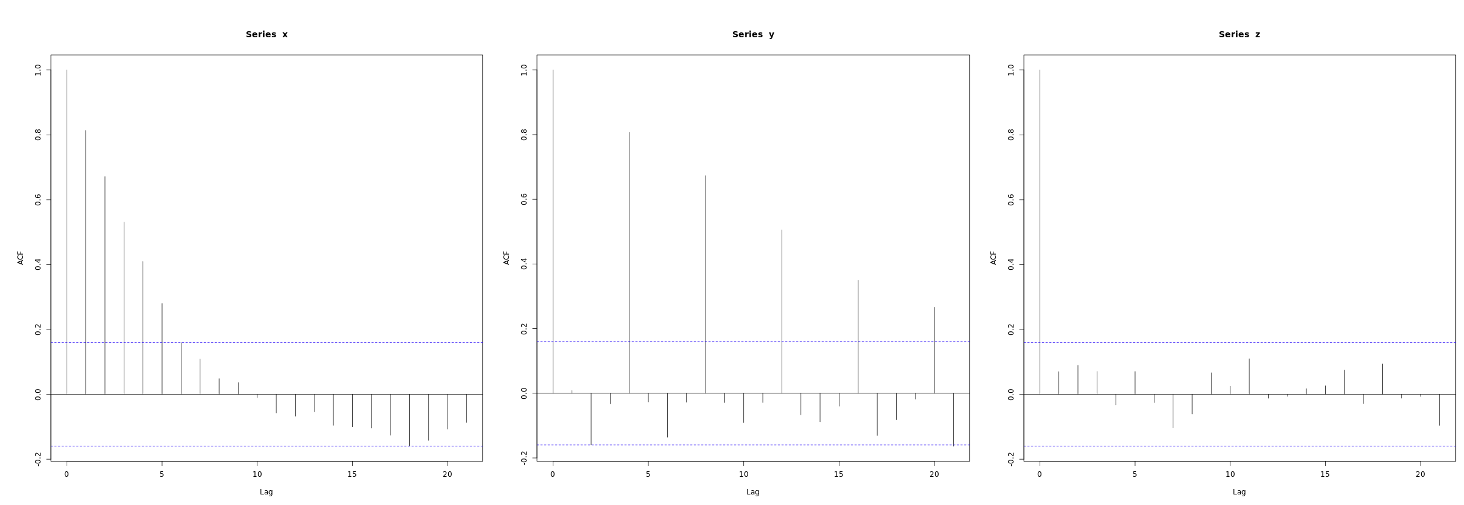
El ACF de x muestra grandes correlaciones positivas para varios rezagos que decaen rápidamente hacia cero.
El ACF de y muestra correlaciones positivas grandes en rezagos que son múltiplos de cuatro, aunque también decaen hacia cero a medida que aumenta el múltiplo de retraso.
El ACF de z es cercano a cero en todos los rezagos. Parece que la serie z no está linealmente relacionada con su pasado, al menos hasta el desfase 20.
24.6.2.1 Formato de datos de series de tiempo
Hasta ahora hemos realizado solo la exploración gráfica de nuestras series de tiempo. Para realizar los siguientes análisis debemos poner en formato zoo (para observaciones ordenadas) a nuestros datos con el paquete zoo.
library(zoo)
dt_zoo <- dt_ts %>%
read.csv.zoo()
wn <- dt_zoo[,"wn"]
rw <- dt_zoo[,"rw"]
ar <- dt_zoo[,"ar"]
ma <- dt_zoo[,"ma"]
arma <- dt_zoo[,"arma"]Podemos hacer algunos gráficos exploratorios con el paquete zoo.
24.6.2.2 ACF en R
Con nuestros datos en formato haremos el cálculo de la función de autocorrelación (ACF) con el paquete forecast.
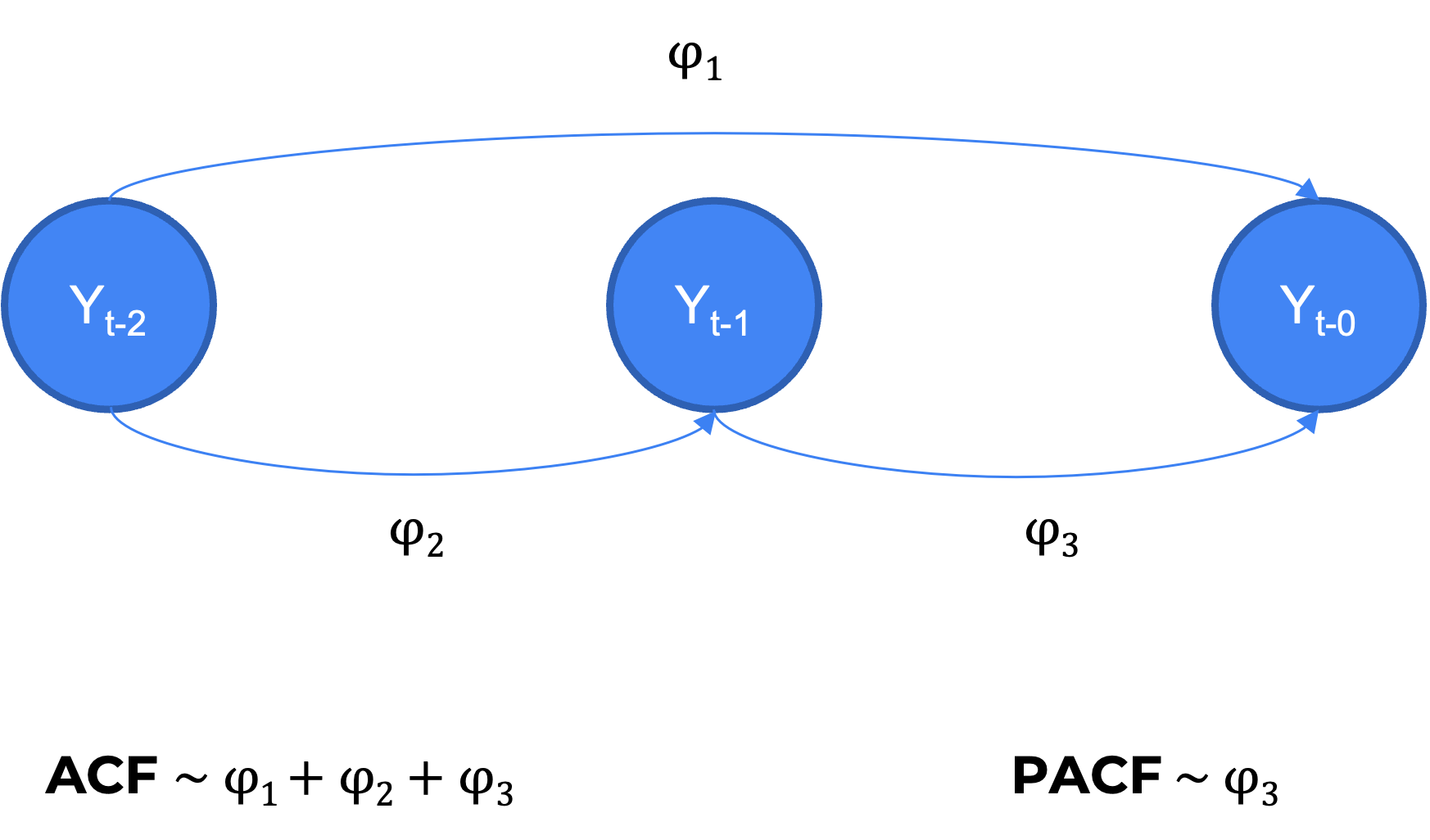
24.6.3 Función de autocorrelación parcial (PACF)
La función de autocorrelación parcial (PACF) es la correlación entre la observación actual y la observación en un rezago (lag) determinado, retirando el efecto de los rezagos precedentes.
24.6.3.1 PACF en R
Podemos hacer el cálculo de la función de autocorrelación arcial (PACF) con el paquete forecast.
24.6.4 Metodologia Box-Jenkins: Definición de modelos
Para la definicion correcta de un modelo ARMA, Box-Jenkins plantearon una metodologia de modelamiento (Box y Jenkins 1976) en 3 etapas :
- Identificacion del modelo
- Estimacion del modelo
- Validacion del modelo
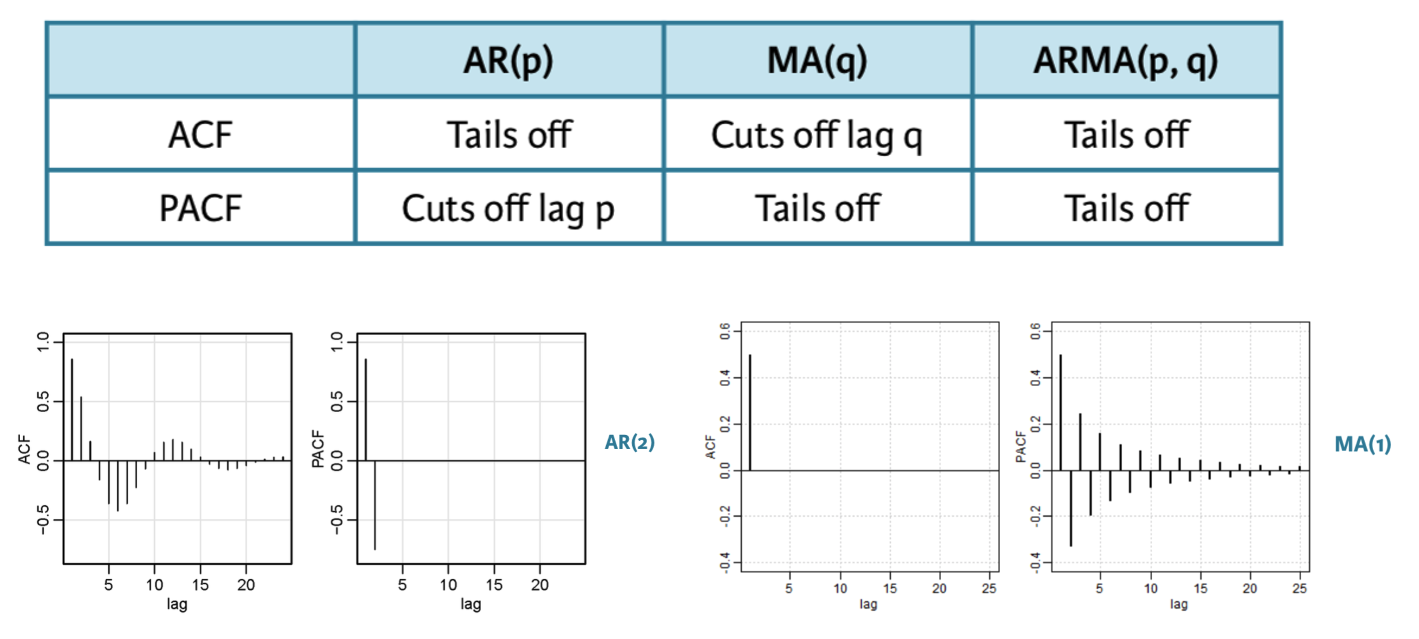
24.6.4.1 Identificacion del modelo
Deacuerdo a Box-jenkins podemos utilizar la ACF y PACF para identificar la correcta parametrización del modelo de nuestra serie de tiempo.
Ahora que conocemos las funciones ggAcf y ggPacf del paquete forecast, podemos utilizar de forma simplificada el comando ggtsdisplay para hacer la exploración completa.
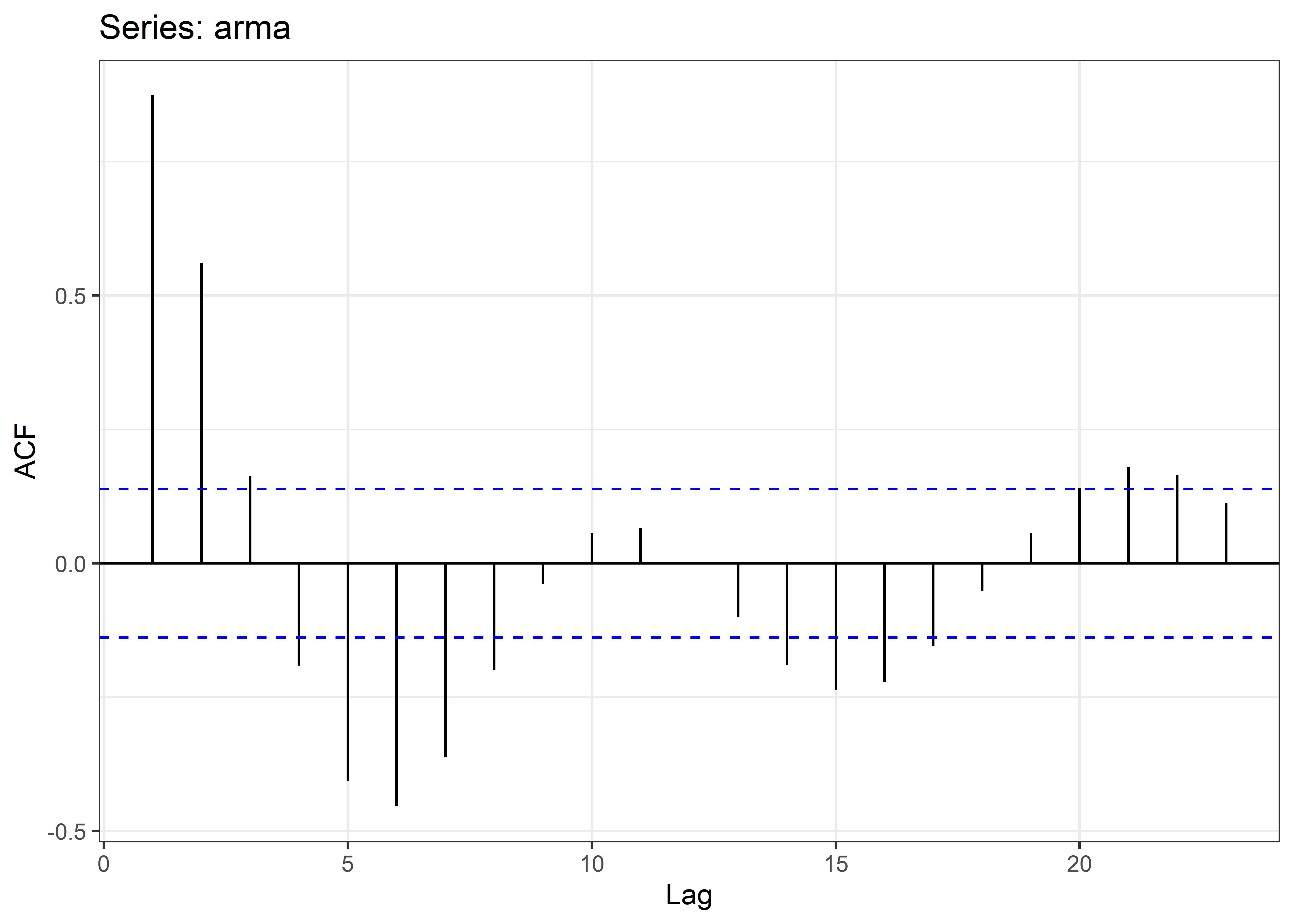
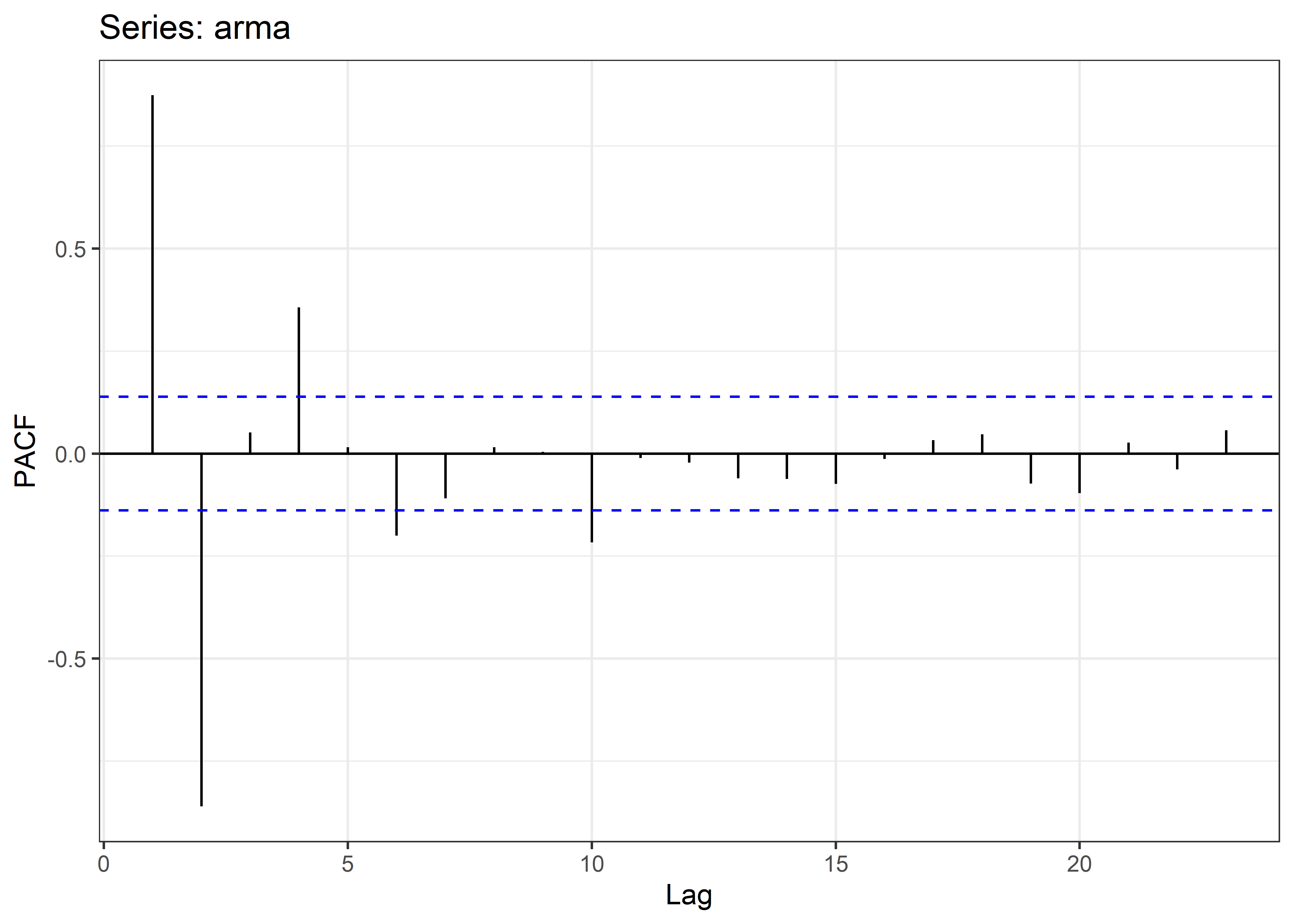
ggtsdisplay(arma)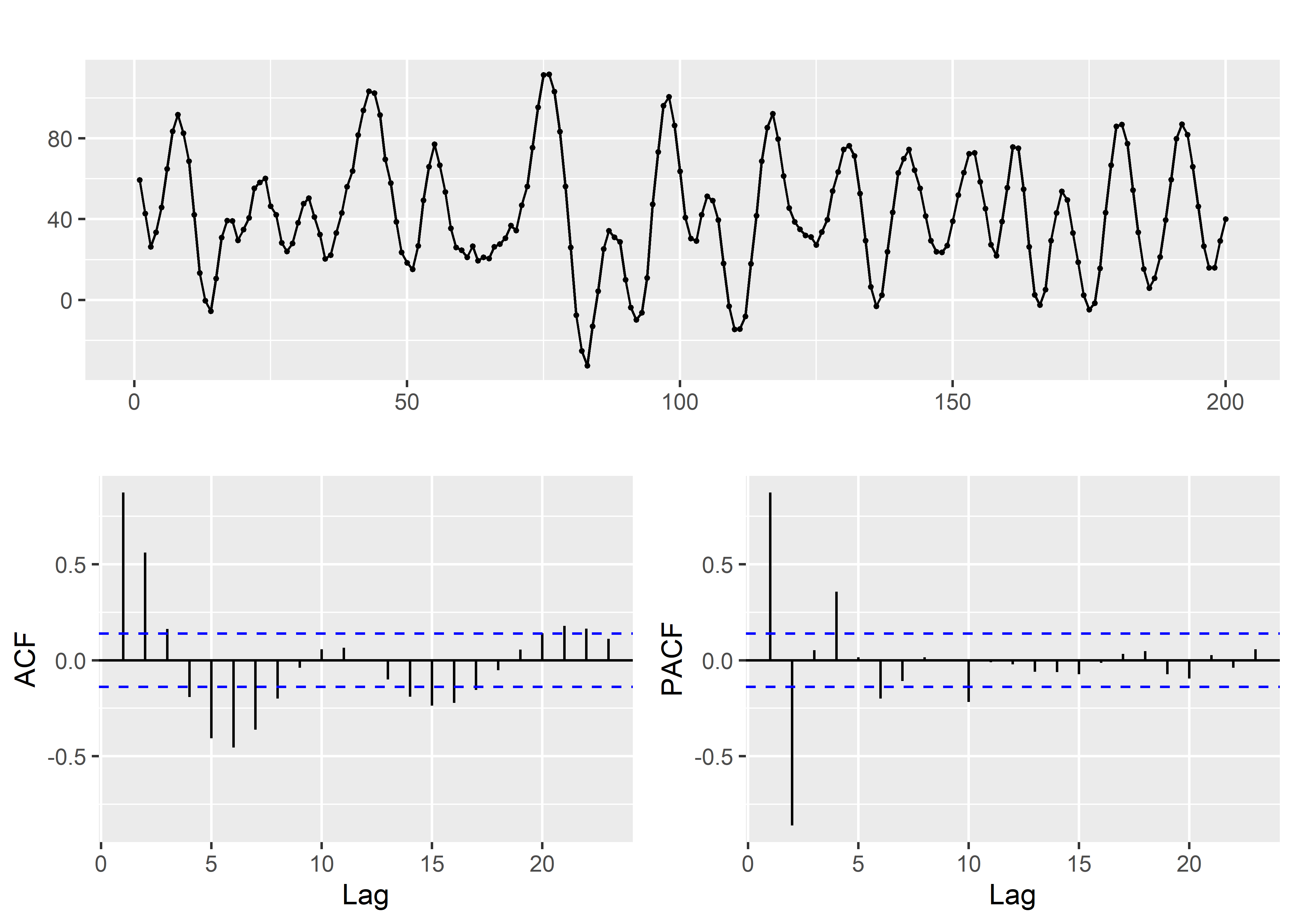
Observamos que esta serie de tiempo parece requerir la parametrizacion de un modelo AR(2) y MA(2).
24.6.4.2 Estimacion del modelo
Una vez identificado visualmente nuestro modelo, procedemos a estimar la espeficacion del modelo ARMA que indico el paso anterior. Para ello usaremos la función Arima del paquete forecast para estimar el modelo con los términos definidos con el ACF y PACF.
24.6.4.3 Validacion del modelo
Por ultimo, en la etapas de la metodologia Box-Jenkins, pasamos a la validación estadística. Asi debemos asegurarnos que los residuales sigan un proceso WN. De lo contrario, no hemos encontrado el mejor modelo.
Esta evaluación se hace mediante los siguientes criterios:
Gráfico de residuales estandarizados (no patrones o periodicidad)
ACF de residuales (no lags significativos)
Q-Q plot de residuales estandarizados (inspeccionar normalidad)
Q-statistics p-value [or plot] (mayoría de lags por encima de umbral de sig.)
Testear el estadistico de Ljung-Box(Ljung y Box 1978), el cual prueba la Hipotesis de que los datos no presentan autocorrelacion serial
Compararemos los resultados de Arima(arma, order = c(2, 0, 2)) frente a un modelo que no tiene una especificación correcta.
Series: arma
ARIMA(0,0,1) with non-zero mean
Coefficients:
ma1 mean
0.9114 42.0357
s.e. 0.0247 2.2049
sigma^2 = 270.1: log likelihood = -843.55
AIC=1693.11 AICc=1693.23 BIC=1703Finalmente, podemos revisar los residuales con la función checkresiduals.
Arima(arma, order = c(2, 0, 2)) %>%
checkresiduals() 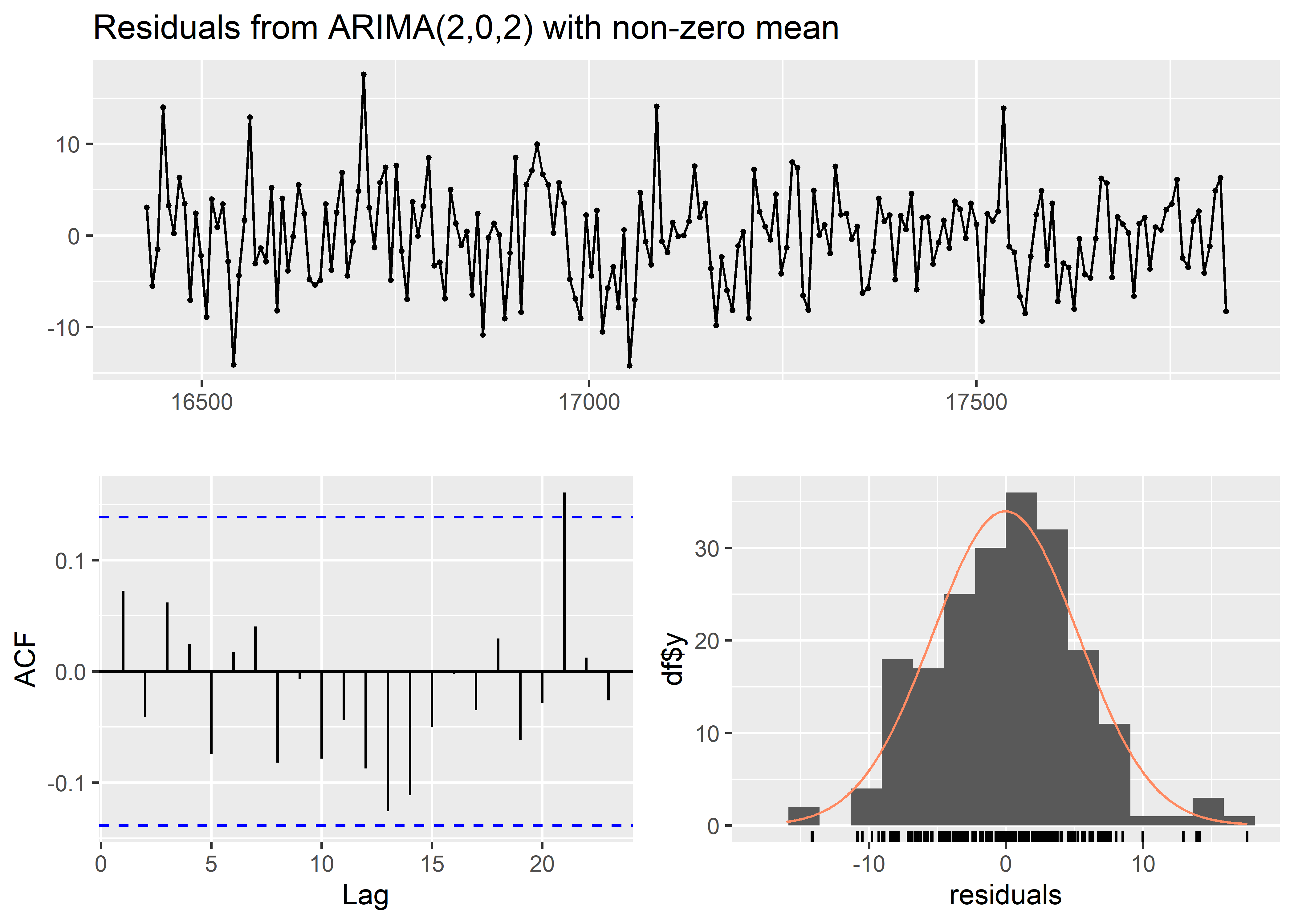
Ljung-Box test
data: Residuals from ARIMA(2,0,2) with non-zero mean
Q* = 6.6095, df = 6, p-value = 0.3585
Model df: 4. Total lags used: 10No observamos ningún patron alarmante en los residuales del modelo, asi mismo el test de Ljung-Box muestra un p-valor > 0.05 indicando que no se puede rechazar la hipotesis de no autocorrelacion serial .
El paquete forecast ofrece una función para automatizar este proceso.
auto.arima(arma)Series: arma
ARIMA(2,0,3) with non-zero mean
Coefficients:
ar1 ar2 ma1 ma2 ma3 mean
1.4947 -0.7834 0.1888 0.8580 0.1246 42.5873
s.e. 0.0556 0.0527 0.0886 0.0536 0.0824 2.8048
sigma^2 = 28.87: log likelihood = -620.84
AIC=1255.67 AICc=1256.25 BIC=1278.76auto.arima(arma) %>%
checkresiduals()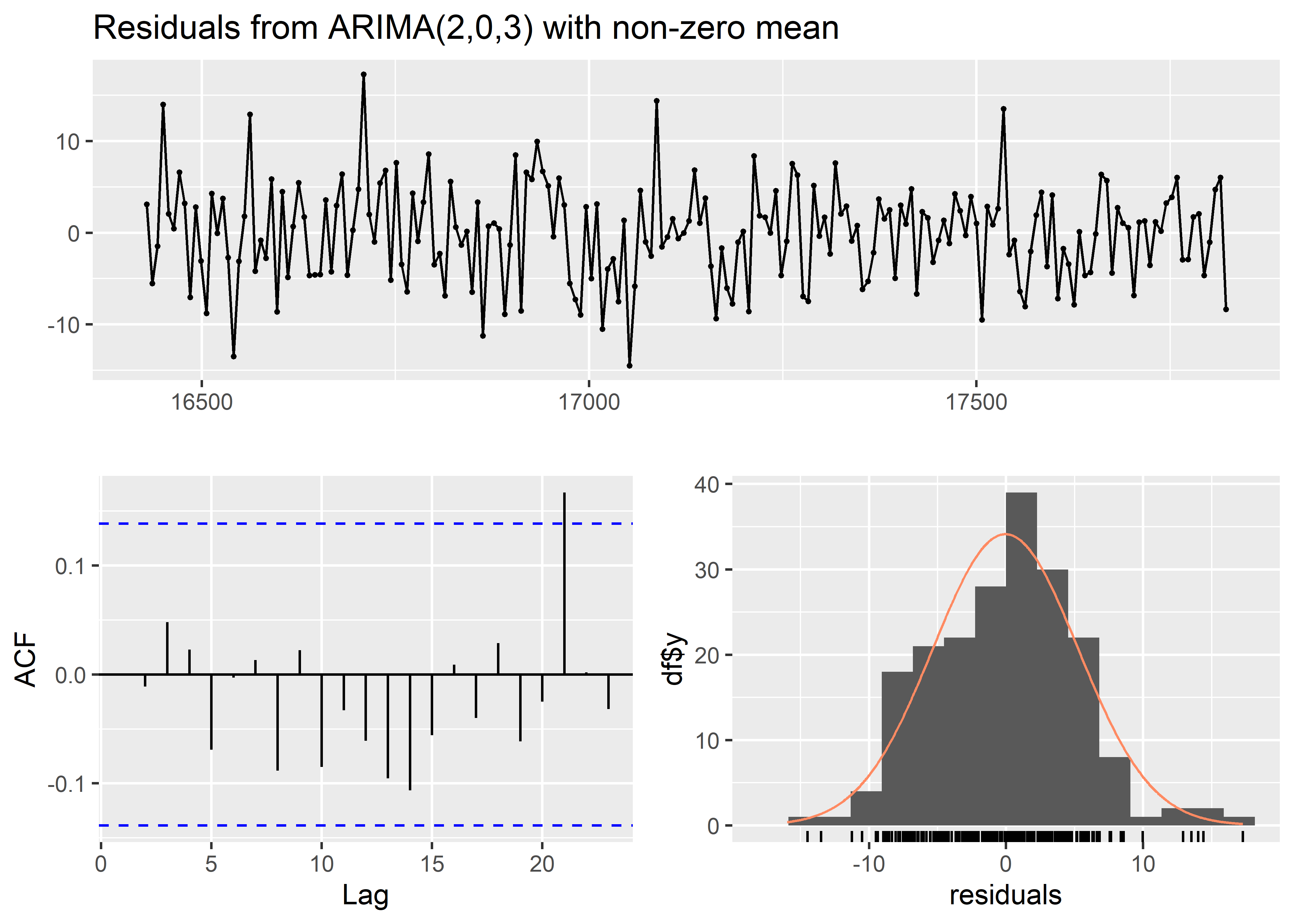
Ljung-Box test
data: Residuals from ARIMA(2,0,3) with non-zero mean
Q* = 4.9023, df = 5, p-value = 0.4279
Model df: 5. Total lags used: 10En caso el modelo propuesto no cumpla la etapa de validacion, se repite nuevamente la secuencia de etapas de la metodologia Box-Jenkins antes señalada hasta obtener una especificación correcta, de encontrarse varias se eligira aquel modelo ARMA que tenga el mejor ajuste en base a criterios de información tales como AIC o BIC.
24.6.5 Modelos ARIMA
Cuando la serie de tiempo es no-estacionaria (vida real) es necesario transformar la serie de datos usando la diferenciación
Una serie temporal exhibe un comportamiento ARIMA si los datos diferenciados tienen un comportamiento ARMA.
La diferencia entre ARMA y ARIMA es la parte de integración. La I (integración) representa el número de veces que se necesita diferenciar a la serie temporal para que esta se torne estacionaria.
Los modelos ARIMA se utilizan ampliamente para el análisis de series de tiempo de la vida real, ya que la mayoría de los datos de series de tiempo no son estacionarios y necesitan diferenciación.
24.6.5.1 Caso Temperatura Global
En primer lugar, empezaremos graficando la serie de tiempo; asi como, las funciones de autocorrelacion y autocorrelacion parcial.
globtemp <- read_csv("data/globtemp.csv") %>%
read.csv.zoo()
globtemp %>%
ggtsdisplay()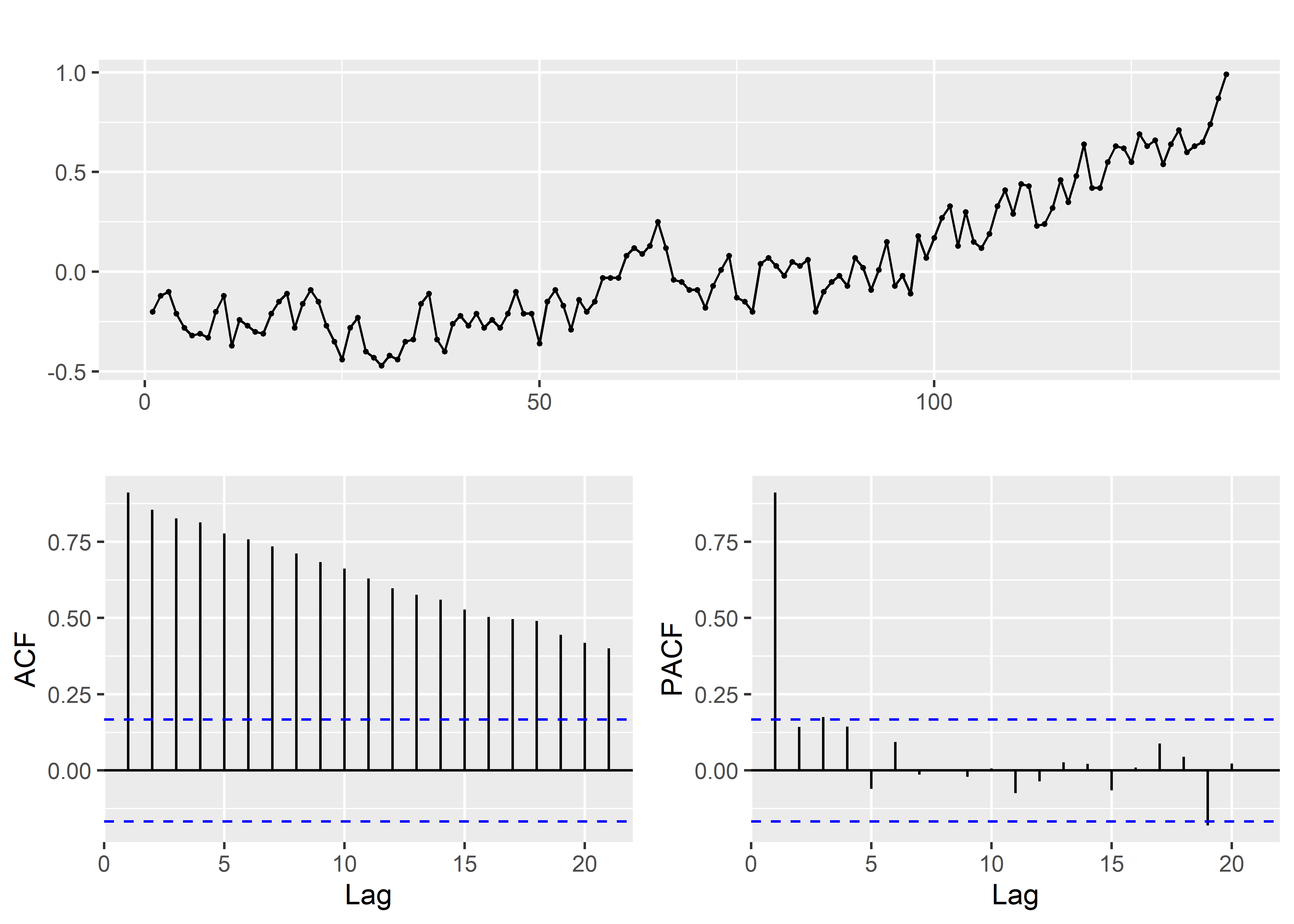
Esta serie de tiempo es claramente no estacionaria.. Por ello, exploraremos diferenciar la serie de tiempo.
globtemp <- read_csv("data/globtemp.csv") %>%
read.csv.zoo()
globtemp %>%
diff() %>%
ggtsdisplay() 
Como se observa hecha la diferenciacion la serie en variaciones obtiene un comportamiento similar a WN.
Después de inspeccionar el ACF y PACF de la serie de datos diferenciada (diff) de globtemp, se puede afirmar que:
Tanto el ACF como el PACF se están reduciendo, lo que implica un modelo ARIMA(1,1,1).
El ACF se corta en el rezago 2 y el PACF se está reduciendo, lo que implica un modelo ARIMA(0,1,2).
El ACF se está reduciendo y el PACF se corta en el rezago 3, lo que implica un modelo ARIMA(3,1,0). Aunque este modelo puede ajustarse razonablemente bien, es el peor de los tres porque utiliza demasiados parámetros para autocorrelaciones tan pequeñas.
Los graficos descriptivos indicarian que el proceso que se esta modelando es integrado de orden 1
Comparamos la estimación de los 3 modelos:
library(broom)
library(purrr)
fit_1 <- Arima(globtemp, order = c(1, 1, 1))
fit_2 <- Arima(globtemp, order = c(0, 1, 2))
fit_3 <- Arima(globtemp, order = c(3, 1, 0))
list(fit_1, fit_2, fit_3) %>%
map_df(glance, .id = "model")# A tibble: 3 × 6
model sigma logLik AIC BIC nobs
<chr> <dbl> <dbl> <dbl> <dbl> <int>
1 1 0.103 118. -229. -221. 136
2 2 0.102 118. -230. -222. 136
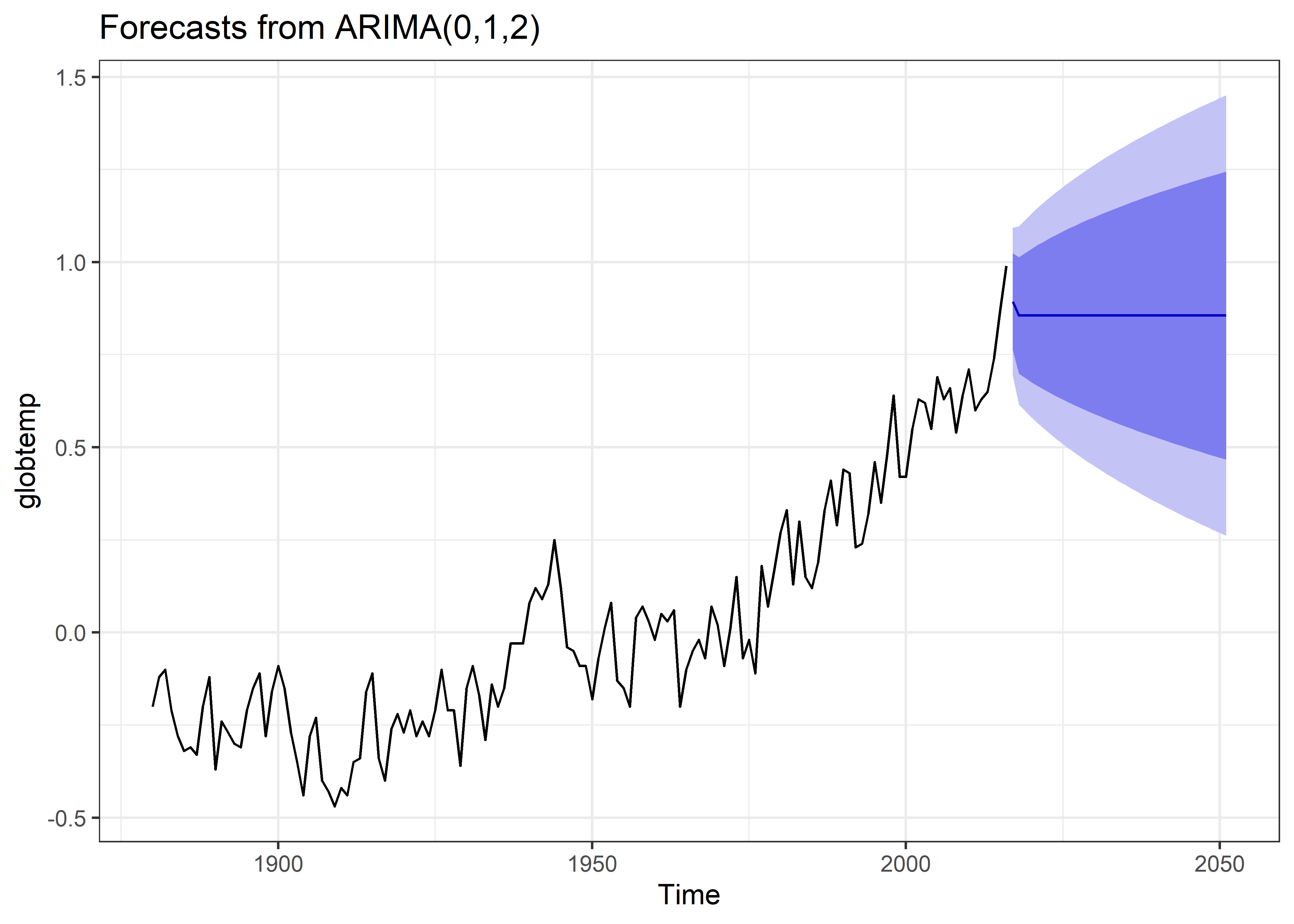
3 3 0.101 120. -231. -219. 136A juzgar por AIC y BIC, el modelo ARIMA(0,1,2) funciona mejor que los otros modelos en los datos de temperatura global(globtemp).
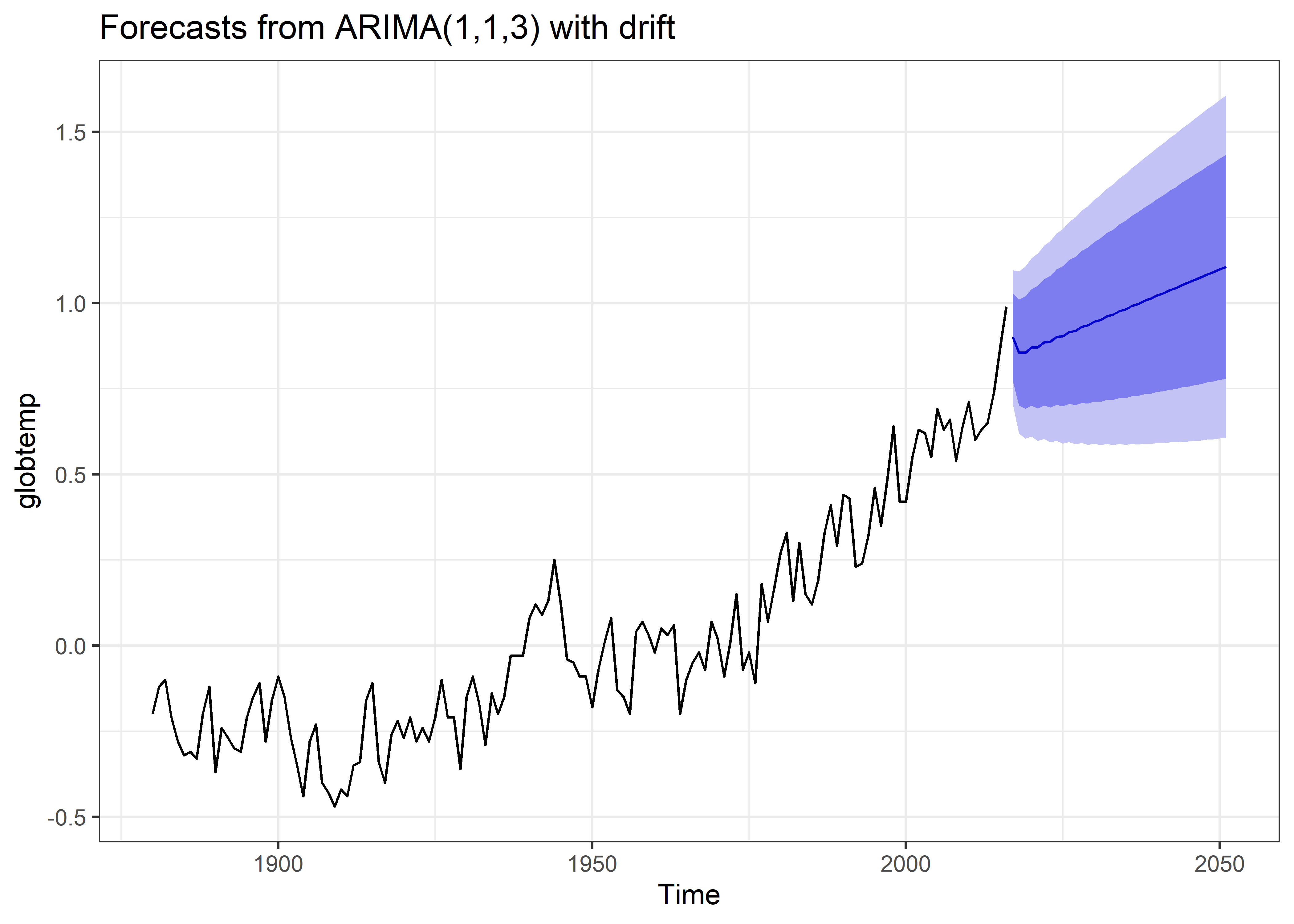
Una vez determinado el modelo de serie de tiempo más adecuado, se procede a utilizarlo para realizar tareas como la predicción de los valores futuros de la serie de tiempo. Para esto usaremos la función forecast y especificaremos el horizonte de predicción (en 35 periodos).
Asimismo tambien podemos calibrar el modelo de forma automática para buscar un mejor modelo para la predicción.